第17章 勾股定理4类题型型 讲义 2023—2024学年人教版数学八年级下册(含答案)
文档属性
| 名称 | 第17章 勾股定理4类题型型 讲义 2023—2024学年人教版数学八年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 310.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 08:25:58 | ||
图片预览

文档简介
勾股定理4题型
勾股定理好用题型
题型1、最短路径问题
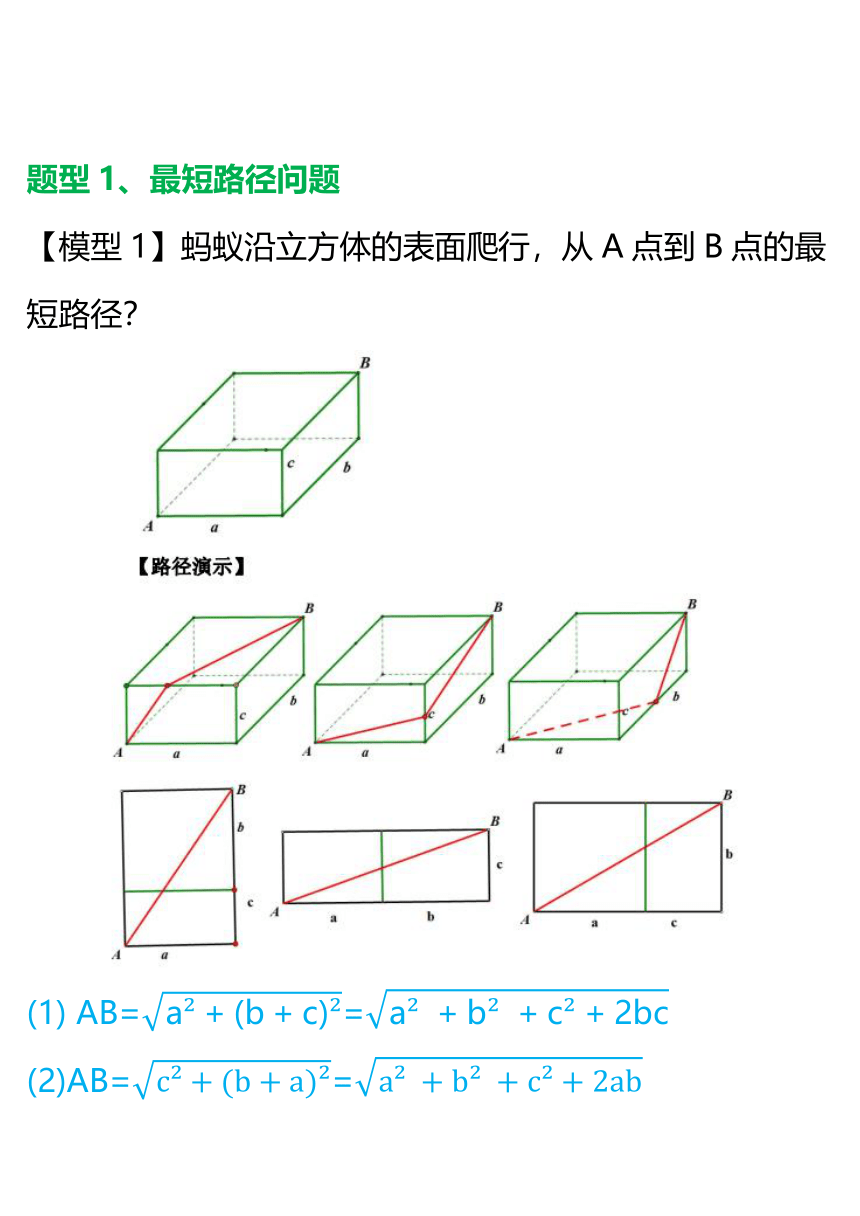
【模型1】蚂蚁沿立方体的表面爬行,从A点到B点的最短路径?
(1) AB==
(2)AB==
(3) AB==
由此可见,ab、bc、ac谁小,则路径就最小。
结论:最短路径=
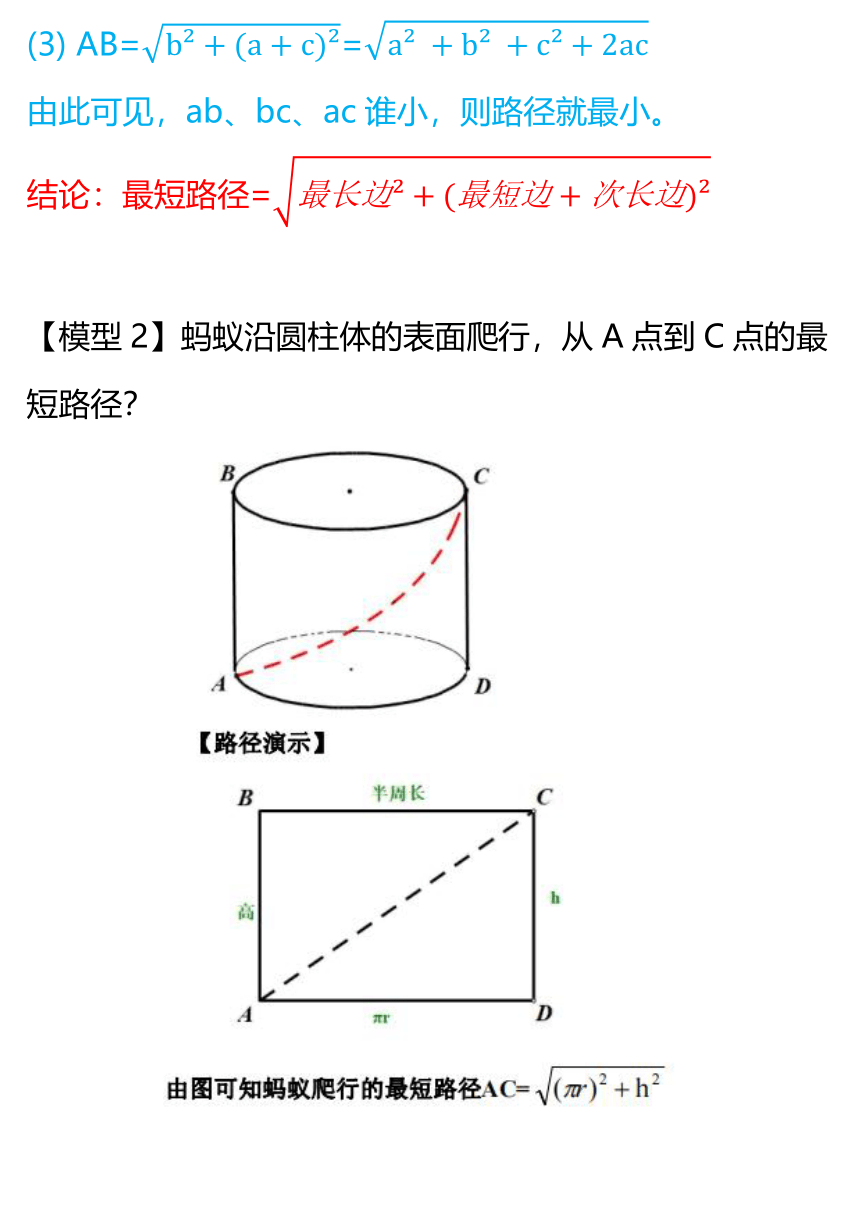
【模型2】蚂蚁沿圆柱体的表面爬行,从A点到C点的最短路径?
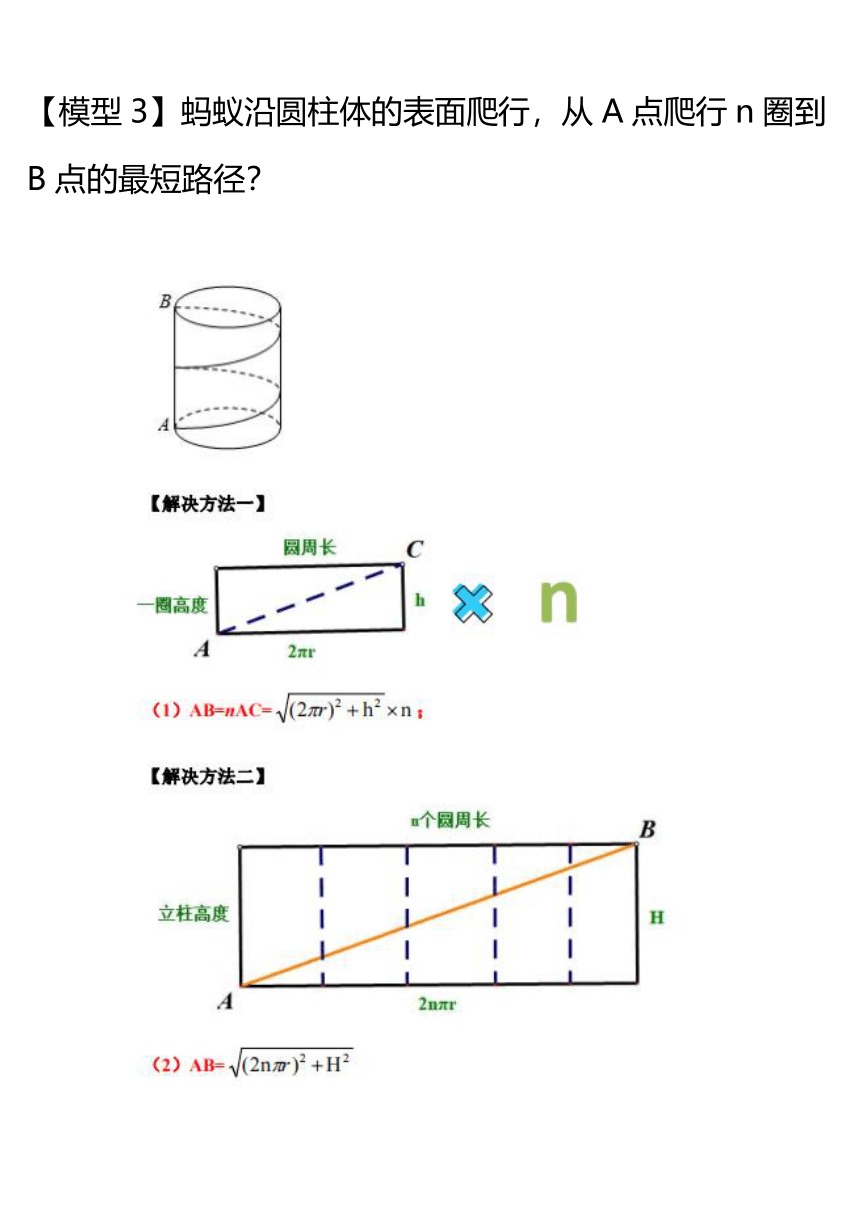
【模型3】蚂蚁沿圆柱体的表面爬行,从A点爬行n圈到B点的最短路径?
结论:最短路径可分圈计算,亦可整体计算。注意:异侧半周长、同侧整周长
【模型4】蚂蚁吃蜂蜜问题:蚂蚁从圆柱体的外壁A处爬行到内壁B处的最短路径?
题型2、折叠模型
【模型1】 如图所示,在Rt△ACB中,已知AC=a,BC=b,D为BC边上一点,沿AD对折,C刚好落在AB边上E点处,求CD的长度。
【解决思路】CD=DE,在Rt△DEB中,利用勾股定理建立方程即可求解。
【模型2】如图,已知ABCD为长方形纸片,CD=3,在CD上存在一点E,沿直线AE将△AED折叠,D恰好落在BC边上的点F处,求EF的长。
【解决思路】DE=DF,在Rt△ECF中,利用勾股定理建立方程即可求解。
【模型3】如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,求FC′。
题型3、赵爽弦图
【结论1】如图所示,在正方形ABCD的四边AB、BC、CD、AD上分别取点E、F、G、H中,使得BE=CF=DG=AH,则四边形EFGH为正方形。
【结论2】如图所示,EQ//NG,FM//HP,则四边形PQMN为正方形。
【结论3】
S正方形ABCD=4S△EAH+S正方形EFGH
S正方形EFGH=4S△EQH+S正方形PQMN
2S正方形EFGH= S正方形ABCD+S正方形PQMN
解决方法:
①赵爽弦图可以证明勾股定理也可以研究如何拼正方形;②一个小正方形加上四个全等的直角三角形能拼成一个大正方形
③大正方形的边长为直角三角形的斜边,小正方形的边长为直角三角形长直角边减去短直角边
题型4、垂美四边形
【结论】对角线互相垂直的四边形叫做“垂美”四边形,如图所示则有:AB2+CD2=AD2+BC2
【证明】∵AC⊥BD
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得:AB +CD =AO +BO +CO +DO ,AD +BC =AO +DO +BO +CO ,∴AB +CD =AD +BC
勾股定理好用题型
题型1、最短路径问题
【模型1】蚂蚁沿立方体的表面爬行,从A点到B点的最短路径?
(1) AB==
(2)AB==
(3) AB==
由此可见,ab、bc、ac谁小,则路径就最小。
结论:最短路径=
【模型2】蚂蚁沿圆柱体的表面爬行,从A点到C点的最短路径?
【模型3】蚂蚁沿圆柱体的表面爬行,从A点爬行n圈到B点的最短路径?
结论:最短路径可分圈计算,亦可整体计算。注意:异侧半周长、同侧整周长
【模型4】蚂蚁吃蜂蜜问题:蚂蚁从圆柱体的外壁A处爬行到内壁B处的最短路径?
题型2、折叠模型
【模型1】 如图所示,在Rt△ACB中,已知AC=a,BC=b,D为BC边上一点,沿AD对折,C刚好落在AB边上E点处,求CD的长度。
【解决思路】CD=DE,在Rt△DEB中,利用勾股定理建立方程即可求解。
【模型2】如图,已知ABCD为长方形纸片,CD=3,在CD上存在一点E,沿直线AE将△AED折叠,D恰好落在BC边上的点F处,求EF的长。
【解决思路】DE=DF,在Rt△ECF中,利用勾股定理建立方程即可求解。
【模型3】如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,求FC′。
题型3、赵爽弦图
【结论1】如图所示,在正方形ABCD的四边AB、BC、CD、AD上分别取点E、F、G、H中,使得BE=CF=DG=AH,则四边形EFGH为正方形。
【结论2】如图所示,EQ//NG,FM//HP,则四边形PQMN为正方形。
【结论3】
S正方形ABCD=4S△EAH+S正方形EFGH
S正方形EFGH=4S△EQH+S正方形PQMN
2S正方形EFGH= S正方形ABCD+S正方形PQMN
解决方法:
①赵爽弦图可以证明勾股定理也可以研究如何拼正方形;②一个小正方形加上四个全等的直角三角形能拼成一个大正方形
③大正方形的边长为直角三角形的斜边,小正方形的边长为直角三角形长直角边减去短直角边
题型4、垂美四边形
【结论】对角线互相垂直的四边形叫做“垂美”四边形,如图所示则有:AB2+CD2=AD2+BC2
【证明】∵AC⊥BD
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得:AB +CD =AO +BO +CO +DO ,AD +BC =AO +DO +BO +CO ,∴AB +CD =AD +BC
