第八章一元二次方程质量检测 2023—2024学年鲁教版(五四制)八年级数学下册(含答案)
文档属性
| 名称 | 第八章一元二次方程质量检测 2023—2024学年鲁教版(五四制)八年级数学下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 60.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览



文档简介
第八章一元二次方程质量监测
一、选择题
1.关于的方程是一元二次方程,则的取值范围是( )
A. B. 且 C. 且 D.
2.方程的根的情况为( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定
3.观察下列表格,一元二次方程的一个解范围是( )
A. B. C. D.
4.关于的方程有一个根是,则的值是( )
A. B. C. D.
5.用配方法解一元二次方程,配方正确的是( )
A. B. C. D.
6.已知和是方程的两个根,则代数式的值是( )
A. B. C. D.
7.已知等腰三角形的腰和底的长分别是一元二次方程的两个根,则该三角形的周长是( )
A. B. C. 或 D. 不能确定
8.若是方程的一个根,则( )
A. B. C. D.
9.某品牌童装调查发现,童装平均每天可售出件,每件盈利元,为了增加盈利,调查发现每件童装降低元,平均每天可以多售出件,要想使平均每天盈利元,那么每件应降价多少元设每天降价为元,则可列方程
A. B.
C. D.
10.如图,中,,,,点从点出发向终点以个单位长度移动,点从点出发向终点以个单位长度移动,、两点同时出发,一点先到达终点时、两点同时停止,则秒后,的面积等于.( )
A. B. C. D. 或
二、填空题
11.关于的方程的一个根是,则的值为 .
12.设,是关于的方程的两个根,且,则 .
13.已知是一元二次方程的两个实数根,则的值是__________.
14.某中学有一块长,宽的矩形空地,计划在这块空地上划分出四分之一的区域种花,小明同学设计方案如图所示,求花带的宽度.设花带的宽为,则可列方程为______.
15.若一元二次方程无实数根,则一次函数的图象不经过第 象限.
16.若,则______.
17.对于实数,定义新运算“”:,如若,则实数的值是______.
18.如图,四边形是一张正方形纸片,其面积为分别在边,,,上顺次截取,连接,,,分别以,,,为轴将纸片向内翻折,得到四边形若四边形的面积为,则______.
三、解答题
19.解下列方程.
; .
20.已知关于的一元二次方程有两个不相等的实数根,.
求的取值范围;
若,求的值.
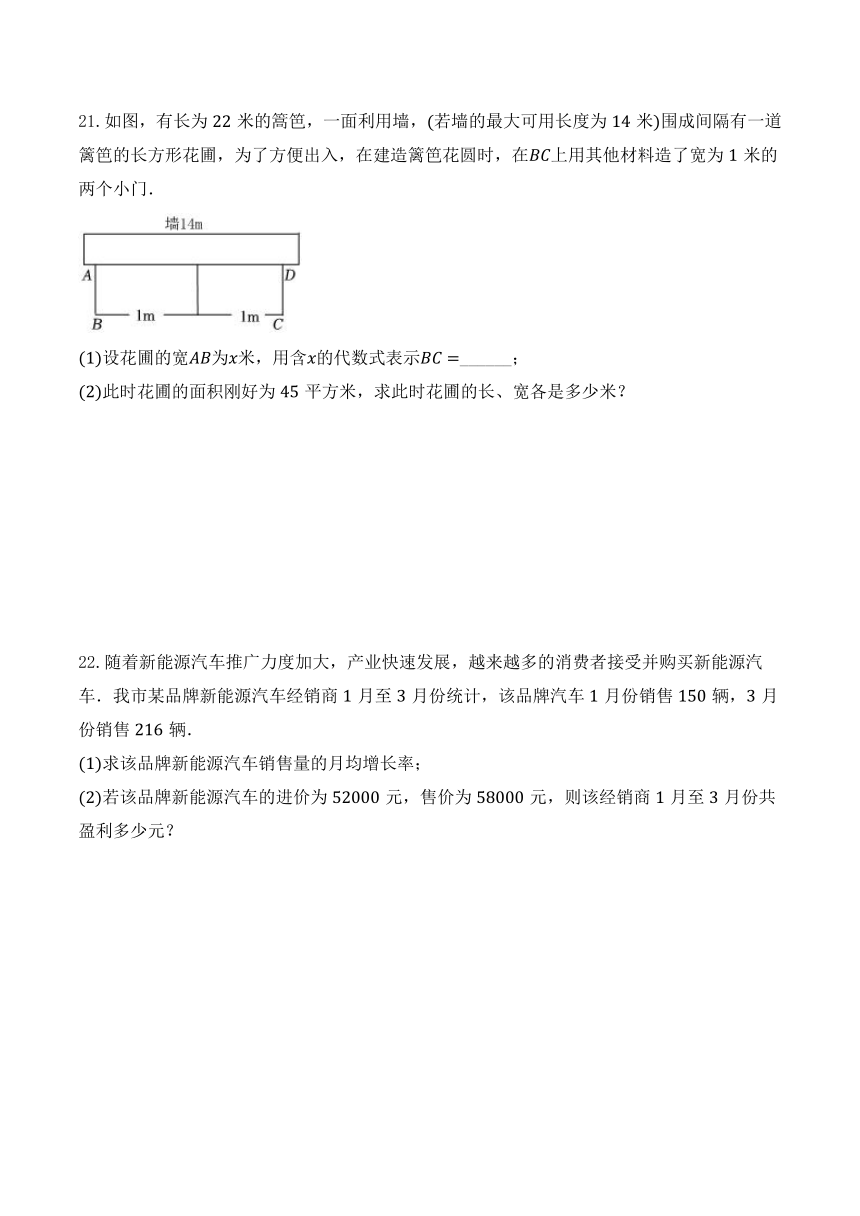
21.如图,有长为米的篙笆,一面利用墙,若墙的最大可用长度为米围成间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圆时,在上用其他材料造了宽为米的两个小门.
设花圃的宽为米,用含的代数式表示______;
此时花圃的面积刚好为平方米,求此时花圃的长、宽各是多少米?
22.随着新能源汽车推广力度加大,产业快速发展,越来越多的消费者接受并购买新能源汽车.我市某品牌新能源汽车经销商月至月份统计,该品牌汽车月份销售辆,月份销售辆.
求该品牌新能源汽车销售量的月均增长率;
若该品牌新能源汽车的进价为元,售价为元,则该经销商月至月份共盈利多少元?
23.某种商品平均每天可销售件,每件盈利元,为了促进销售,商场决定采取适当的降价措施,经调查发现,每件商品毎降价元,商场平均每天可多售出件,设每件商品降价元.据此规律,请回答:
降价后,每件商品盈利______元,日销售量______件.用含的代数式表示;
在上述条件不变的情况下,要更大程度地让利顾客,每件商品降价多少元时,商场日盈利可达到元?
24.利用我们学过的完全平方公式与不等式知识能解决方程或代数式的一些问题,阅读下列两则材料:
材料一:已知,求、的值.
解:,
,
,
,
,
.
材料二:探索代数式与是否存在最大值或最小值?
,,.
代数式有最小值;
,,.
代数式有最大值.
学习方法并完成下列问题:
代数式的最小值为______;
如图,在紧靠围墙的空地上,利用围墙及一段长为米的木栅栏围成一个长方形花圃,为了设计一个尽可能大的花圃,设长方形垂直于围墙的一边长度为米,则花圃的最大面积是多少?
已知的三条边的长度分别为,,,且,且为正整数,求周长的最小值.
答案
2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15. 一
16.
17.
18.
19. 解:,
,
或,
,;
,
,
或,
,.
20. 解:关于的一元二次方程有两个不相等的实数根,.
,
解得:;
和是一元二次方程的两根,
,,
,
,
,
解得:,,
,
.
21. 解:;
,
化简得:,
解得:,.
当时,,符合要求;
当时,,不符合要求,舍去.
长为:米
答:花圃的宽为米,长为米.
22. 解:设该品牌新能源汽车销售量的月均增长率,
依题意,得:,
解得:,舍去.
答:该品牌新能源汽车销售量的月均增长率为.
月份的销售量为辆,
元.
答:该经销商月至月份共盈利元.
23. ;;
根据题意可得,
解得:或,
该商场为了尽快减少库存,
降的越多,越吸引顾客,
选,
答:每件商品降价元,商场日盈利可达元.
24. (1)
(2)1250平方米
(3)15
一、选择题
1.关于的方程是一元二次方程,则的取值范围是( )
A. B. 且 C. 且 D.
2.方程的根的情况为( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定
3.观察下列表格,一元二次方程的一个解范围是( )
A. B. C. D.
4.关于的方程有一个根是,则的值是( )
A. B. C. D.
5.用配方法解一元二次方程,配方正确的是( )
A. B. C. D.
6.已知和是方程的两个根,则代数式的值是( )
A. B. C. D.
7.已知等腰三角形的腰和底的长分别是一元二次方程的两个根,则该三角形的周长是( )
A. B. C. 或 D. 不能确定
8.若是方程的一个根,则( )
A. B. C. D.
9.某品牌童装调查发现,童装平均每天可售出件,每件盈利元,为了增加盈利,调查发现每件童装降低元,平均每天可以多售出件,要想使平均每天盈利元,那么每件应降价多少元设每天降价为元,则可列方程
A. B.
C. D.
10.如图,中,,,,点从点出发向终点以个单位长度移动,点从点出发向终点以个单位长度移动,、两点同时出发,一点先到达终点时、两点同时停止,则秒后,的面积等于.( )
A. B. C. D. 或
二、填空题
11.关于的方程的一个根是,则的值为 .
12.设,是关于的方程的两个根,且,则 .
13.已知是一元二次方程的两个实数根,则的值是__________.
14.某中学有一块长,宽的矩形空地,计划在这块空地上划分出四分之一的区域种花,小明同学设计方案如图所示,求花带的宽度.设花带的宽为,则可列方程为______.
15.若一元二次方程无实数根,则一次函数的图象不经过第 象限.
16.若,则______.
17.对于实数,定义新运算“”:,如若,则实数的值是______.
18.如图,四边形是一张正方形纸片,其面积为分别在边,,,上顺次截取,连接,,,分别以,,,为轴将纸片向内翻折,得到四边形若四边形的面积为,则______.
三、解答题
19.解下列方程.
; .
20.已知关于的一元二次方程有两个不相等的实数根,.
求的取值范围;
若,求的值.
21.如图,有长为米的篙笆,一面利用墙,若墙的最大可用长度为米围成间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圆时,在上用其他材料造了宽为米的两个小门.
设花圃的宽为米,用含的代数式表示______;
此时花圃的面积刚好为平方米,求此时花圃的长、宽各是多少米?
22.随着新能源汽车推广力度加大,产业快速发展,越来越多的消费者接受并购买新能源汽车.我市某品牌新能源汽车经销商月至月份统计,该品牌汽车月份销售辆,月份销售辆.
求该品牌新能源汽车销售量的月均增长率;
若该品牌新能源汽车的进价为元,售价为元,则该经销商月至月份共盈利多少元?
23.某种商品平均每天可销售件,每件盈利元,为了促进销售,商场决定采取适当的降价措施,经调查发现,每件商品毎降价元,商场平均每天可多售出件,设每件商品降价元.据此规律,请回答:
降价后,每件商品盈利______元,日销售量______件.用含的代数式表示;
在上述条件不变的情况下,要更大程度地让利顾客,每件商品降价多少元时,商场日盈利可达到元?
24.利用我们学过的完全平方公式与不等式知识能解决方程或代数式的一些问题,阅读下列两则材料:
材料一:已知,求、的值.
解:,
,
,
,
,
.
材料二:探索代数式与是否存在最大值或最小值?
,,.
代数式有最小值;
,,.
代数式有最大值.
学习方法并完成下列问题:
代数式的最小值为______;
如图,在紧靠围墙的空地上,利用围墙及一段长为米的木栅栏围成一个长方形花圃,为了设计一个尽可能大的花圃,设长方形垂直于围墙的一边长度为米,则花圃的最大面积是多少?
已知的三条边的长度分别为,,,且,且为正整数,求周长的最小值.
答案
2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15. 一
16.
17.
18.
19. 解:,
,
或,
,;
,
,
或,
,.
20. 解:关于的一元二次方程有两个不相等的实数根,.
,
解得:;
和是一元二次方程的两根,
,,
,
,
,
解得:,,
,
.
21. 解:;
,
化简得:,
解得:,.
当时,,符合要求;
当时,,不符合要求,舍去.
长为:米
答:花圃的宽为米,长为米.
22. 解:设该品牌新能源汽车销售量的月均增长率,
依题意,得:,
解得:,舍去.
答:该品牌新能源汽车销售量的月均增长率为.
月份的销售量为辆,
元.
答:该经销商月至月份共盈利元.
23. ;;
根据题意可得,
解得:或,
该商场为了尽快减少库存,
降的越多,越吸引顾客,
选,
答:每件商品降价元,商场日盈利可达元.
24. (1)
(2)1250平方米
(3)15
