第三章 图形的平移与旋转 单元练习 2023—2024学年北师大版数学八年级下册(无答案)
文档属性
| 名称 | 第三章 图形的平移与旋转 单元练习 2023—2024学年北师大版数学八年级下册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 08:04:37 | ||
图片预览

文档简介
山东滕州2023-2024学年第二学期八年级数学单元测试题
第三章:图形的平移与旋转
一、单选题
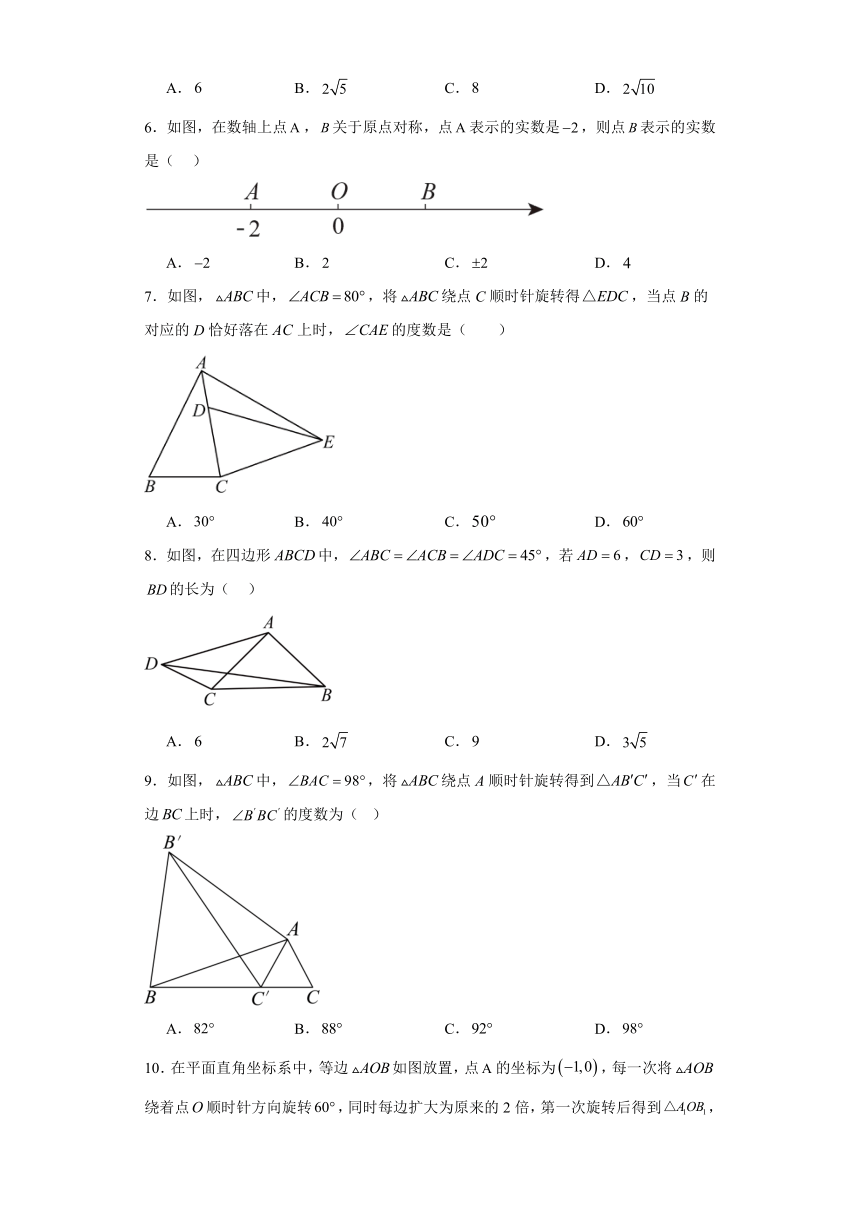
1.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.以原点为中心,把点逆时针旋转,得到点B,则点B的坐标为( )
A. B. C. D.
3.如图,直线、相交于点O.已知,把分成两个角,且,将射线绕点O逆时针旋转到,当时,则是( ).
A.70 B.80 C.90 D.100
4.如图,将周长为的沿边向右移动,得到,则四边形的周长是( ).
A.17 B.19 C.22 D.24
5.如图,在中,,,,将绕点A逆时针旋转,使点落在线段上的点处,点落在点处,则、两点间的距离为( )
A. B. C. D.
6.如图,在数轴上点,关于原点对称,点表示的实数是,则点表示的实数是( )
A. B. C. D.
7.如图,中,,将绕点C顺时针旋转得,当点B的对应的D恰好落在上时,的度数是( )
A. B. C. D.
8.如图,在四边形中,,若,,则的长为( )
A. B. C. D.
9.如图,中,,将绕点A顺时针旋转得到,当在边上时,的度数为( )
A. B. C. D.
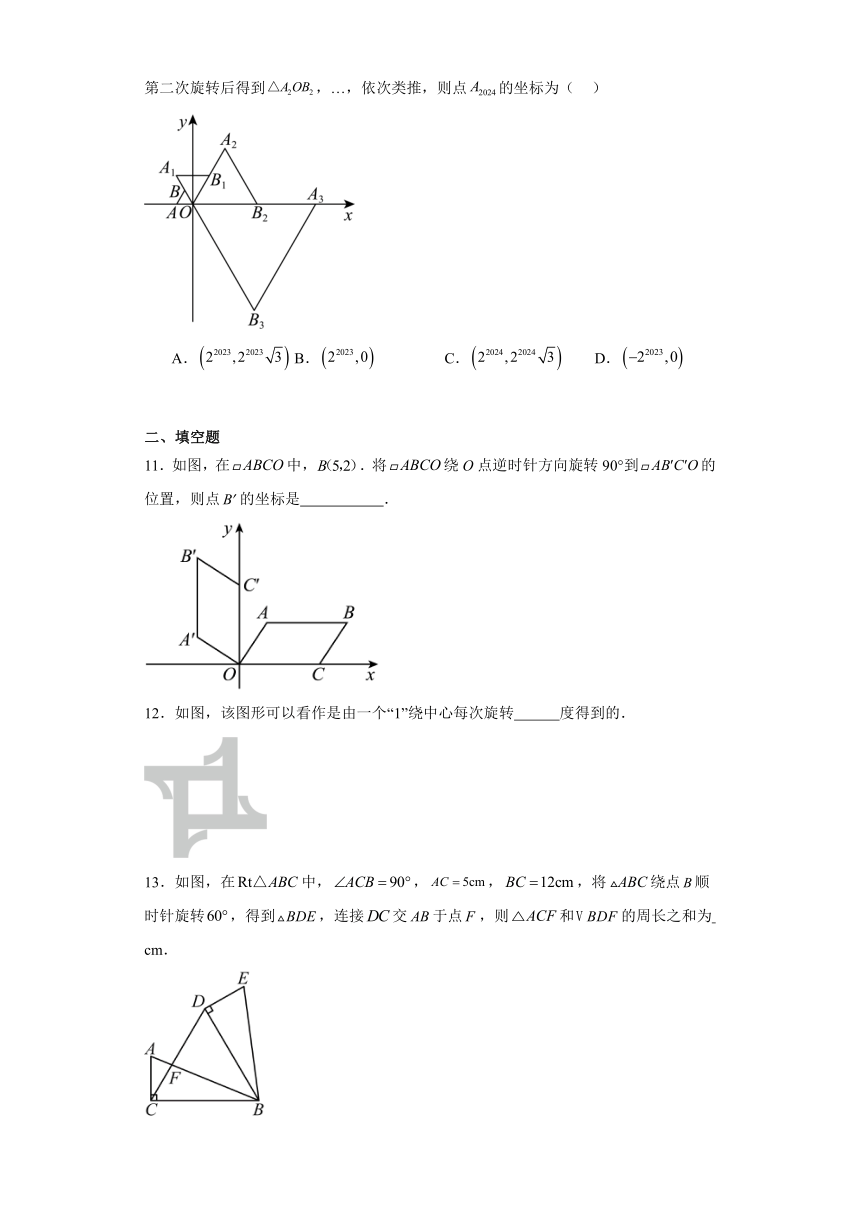
10.在平面直角坐标系中,等边如图放置,点的坐标为,每一次将绕着点顺时针方向旋转,同时每边扩大为原来的2倍,第一次旋转后得到,第二次旋转后得到,…,依次类推,则点的坐标为( )
A. B. C. D.
二、填空题
11.如图,在中,.将绕O点逆时针方向旋转90°到的位置,则点的坐标是 .
12.如图,该图形可以看作是由一个“1”绕中心每次旋转 度得到的.
13.如图,在中,,,,将绕点顺时针旋转,得到,连接交于点,则和的周长之和为 cm.
14.直角坐标系中,点关于坐标原点成中心对称的点的坐标是 .
15.如图,将直角三角形沿边向右平移得到直角三角形,交于点G.若,,,则图中阴影部分的面积为 .
16.如图,在平面直角坐标系中,将直角三角板的角的顶点与坐标原点O重合,直角顶点B在x轴的负半轴上,顶点A在第三象限.将绕点O逆时针旋转一定角度得到使点B的对应点落在边上.若,则点的坐标为 .
17.如图,已知为等边三角形,将边绕点顺时针旋转得到线段,连接,与交于,的平分线交于点,点为上一点,则 .
18.如图,和都是等边三角形,,,边,位于同一条直线上,点与点重合.现将固定不动,把自左向右沿直线平移,移出外(点与重合)时停止移动.在移动过程中,当两个三角形重合部分的面积为时,平移的距离是 .
三、解答题
19.如图是2×3的正方形网格,的顶点都在格点上,按下列要求画图.
(1)在图1中画,使与关于某条直线成轴对称;
(2)在图2中画,使与关于某点成中心对称.
20.如图,在平面直角坐标系中,的三个顶点分别为,,.
(1)画出关于x轴对称的,并写出点的坐标;
(2)画出向右平移6个单位长度,再向上平移2个单位长度后的,并写出点的坐标;
(3)求出的面积.
21.如图,将三角形沿的方向平移得到三角形.
(1)若,求的度数;
(2)若,,求三角形平移的距离.
22.为实现“绿色江夏·和谐江夏”,江夏区政府准备开发城北一块长为,宽为的长方形空地.
(1)方案一:如图1,将这块空地种上草坪,中间修一条弯曲的小路,小路的左边线向右平移就是它的右边线.则这块草地的面积为 ;
(2)方案二:如图2,将这块空地种上草坪,修纵横两条宽的小路,则这块草地的面积为 ;
(3)方案三:修建一个长是宽的倍,面积为的篮球场,若比赛用的篮球场要求长在到之间,宽在到之间.这个篮球场能用做比赛吗?并说明理由.
23.如图,在四边形中,,将绕点顺时针旋转一定角度后,点的对应点恰好与点重合,得到,与交于点,与交于点.
(1)求证:;
(2)若,,求四边形的对角线的长.
24.在平面直角坐标系中,点A的坐标为,点是x轴上一动点,是等腰直角三角形,,,点C在直线的右侧,以C为中心,将线段绕点C顺时针旋转得到线段,点A的对应点是点P,连接.
(1)如图1,若点B的坐标为,C点坐标是______.
(2)如图2,若与x轴正半轴夹角是,求m的值.
第三章:图形的平移与旋转
一、单选题
1.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.以原点为中心,把点逆时针旋转,得到点B,则点B的坐标为( )
A. B. C. D.
3.如图,直线、相交于点O.已知,把分成两个角,且,将射线绕点O逆时针旋转到,当时,则是( ).
A.70 B.80 C.90 D.100
4.如图,将周长为的沿边向右移动,得到,则四边形的周长是( ).
A.17 B.19 C.22 D.24
5.如图,在中,,,,将绕点A逆时针旋转,使点落在线段上的点处,点落在点处,则、两点间的距离为( )
A. B. C. D.
6.如图,在数轴上点,关于原点对称,点表示的实数是,则点表示的实数是( )
A. B. C. D.
7.如图,中,,将绕点C顺时针旋转得,当点B的对应的D恰好落在上时,的度数是( )
A. B. C. D.
8.如图,在四边形中,,若,,则的长为( )
A. B. C. D.
9.如图,中,,将绕点A顺时针旋转得到,当在边上时,的度数为( )
A. B. C. D.
10.在平面直角坐标系中,等边如图放置,点的坐标为,每一次将绕着点顺时针方向旋转,同时每边扩大为原来的2倍,第一次旋转后得到,第二次旋转后得到,…,依次类推,则点的坐标为( )
A. B. C. D.
二、填空题
11.如图,在中,.将绕O点逆时针方向旋转90°到的位置,则点的坐标是 .
12.如图,该图形可以看作是由一个“1”绕中心每次旋转 度得到的.
13.如图,在中,,,,将绕点顺时针旋转,得到,连接交于点,则和的周长之和为 cm.
14.直角坐标系中,点关于坐标原点成中心对称的点的坐标是 .
15.如图,将直角三角形沿边向右平移得到直角三角形,交于点G.若,,,则图中阴影部分的面积为 .
16.如图,在平面直角坐标系中,将直角三角板的角的顶点与坐标原点O重合,直角顶点B在x轴的负半轴上,顶点A在第三象限.将绕点O逆时针旋转一定角度得到使点B的对应点落在边上.若,则点的坐标为 .
17.如图,已知为等边三角形,将边绕点顺时针旋转得到线段,连接,与交于,的平分线交于点,点为上一点,则 .
18.如图,和都是等边三角形,,,边,位于同一条直线上,点与点重合.现将固定不动,把自左向右沿直线平移,移出外(点与重合)时停止移动.在移动过程中,当两个三角形重合部分的面积为时,平移的距离是 .
三、解答题
19.如图是2×3的正方形网格,的顶点都在格点上,按下列要求画图.
(1)在图1中画,使与关于某条直线成轴对称;
(2)在图2中画,使与关于某点成中心对称.
20.如图,在平面直角坐标系中,的三个顶点分别为,,.
(1)画出关于x轴对称的,并写出点的坐标;
(2)画出向右平移6个单位长度,再向上平移2个单位长度后的,并写出点的坐标;
(3)求出的面积.
21.如图,将三角形沿的方向平移得到三角形.
(1)若,求的度数;
(2)若,,求三角形平移的距离.
22.为实现“绿色江夏·和谐江夏”,江夏区政府准备开发城北一块长为,宽为的长方形空地.
(1)方案一:如图1,将这块空地种上草坪,中间修一条弯曲的小路,小路的左边线向右平移就是它的右边线.则这块草地的面积为 ;
(2)方案二:如图2,将这块空地种上草坪,修纵横两条宽的小路,则这块草地的面积为 ;
(3)方案三:修建一个长是宽的倍,面积为的篮球场,若比赛用的篮球场要求长在到之间,宽在到之间.这个篮球场能用做比赛吗?并说明理由.
23.如图,在四边形中,,将绕点顺时针旋转一定角度后,点的对应点恰好与点重合,得到,与交于点,与交于点.
(1)求证:;
(2)若,,求四边形的对角线的长.
24.在平面直角坐标系中,点A的坐标为,点是x轴上一动点,是等腰直角三角形,,,点C在直线的右侧,以C为中心,将线段绕点C顺时针旋转得到线段,点A的对应点是点P,连接.
(1)如图1,若点B的坐标为,C点坐标是______.
(2)如图2,若与x轴正半轴夹角是,求m的值.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
