四川省眉山市仁寿县2023-2024学年九年级下学期4月月考数学试题(无答案)
文档属性
| 名称 | 四川省眉山市仁寿县2023-2024学年九年级下学期4月月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 358.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 19:31:37 | ||
图片预览

文档简介
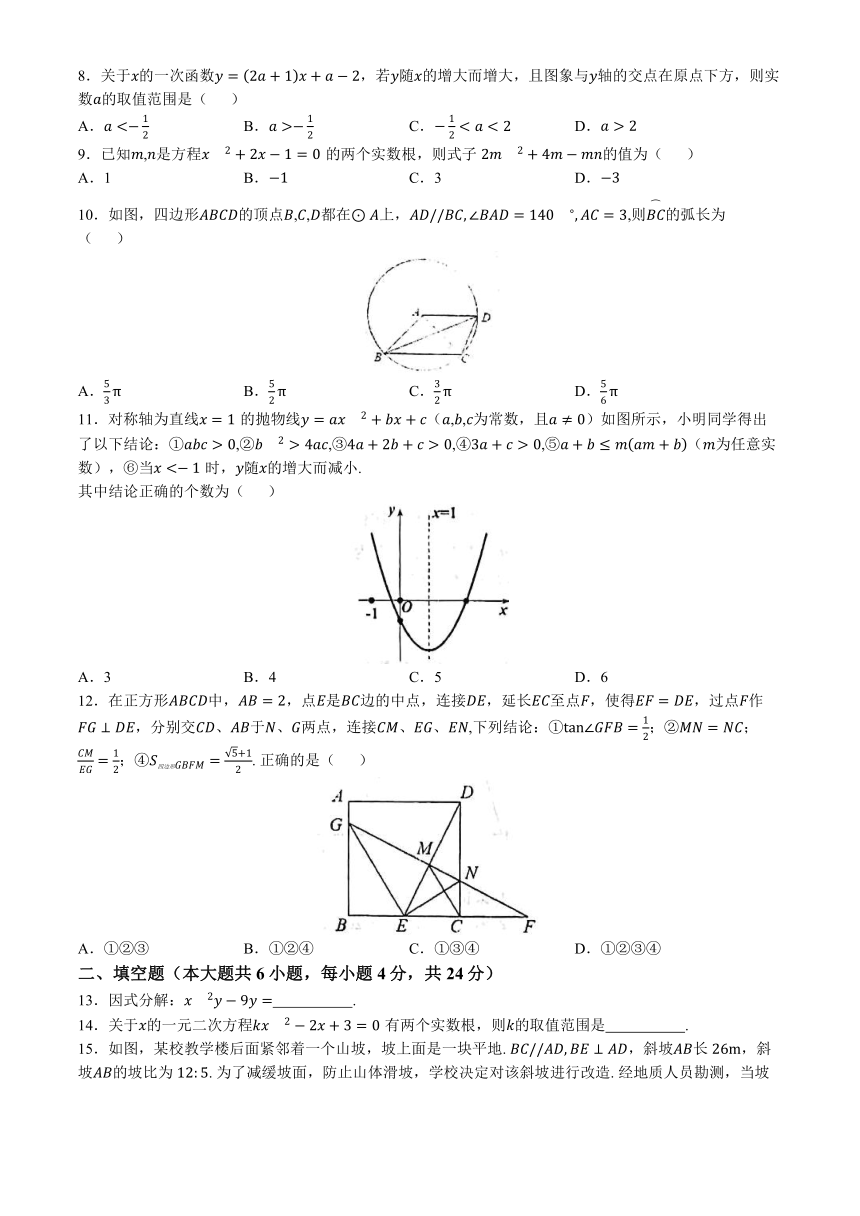
2021级4月教学质量监测
九年级(下)数学试题 2024.4
考试时间 120分钟 总分 150分
一、选择题(本大题共12个小题,每小题4分,共48分)
1.下列实数:,其中最小的是( )
A. B.0 C. D.
2.2022年12月31日,仁寿县户籍人口为150.13万人. 其中数据150.13万用科学记数法表示为( )
A. B. C. D.
3.下面计算正确的是( )
A. B. C. D.
4.如图,直线,且于点,若,则的度数为( )
A. B. C. D.
5.如图是由一个长方体和一个圆柱组成的几何体,它的俯视图是 ( )
A. B. C. D.
6.为了解学生的身体素质状况,国家每年都会进行中小学生身体素质抽测. 在今年的抽测中,某校九年级二班随机抽取了10名男生进行引体向上测试,他们的成绩(单位:个)如下:7,11,10,11,6,14,11,10,11,9. 根据这组数据判断下列结论中错误的是( )
A.这组数据的众数是11 B.这组数据的中位数是10
C.这组数据的平均数是10 D.这组数据的方差是4.6
7.《九章算术》中记载了一种测量井深的方法. 如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸,视线与井口的直径交于点,如果测得米,米,米,那么井深为( )米.
A.7.5 B.7 C.6.5 D.6
8.关于的一次函数,若随的增大而增大,且图象与轴的交点在原点下方,则实数的取值范围是( )
A. B. C. D.
9.已知,是方程的两个实数根,则式子的值为( )
A.1 B. C.3 D.
10.如图,四边形的顶点,,都在上,,则的弧长为 ( )
A. B. C. D.
11.对称轴为直线的抛物线(,,为常数,且)如图所示,小明同学得出了以下结论:①,②,③,④,⑤(为任意实数),⑥当时,随的增大而减小.
其中结论正确的个数为( )
A.3 B.4 C.5 D.6
12.在正方形中,,点是边的中点,连接,延长至点,使得,过点作,分别交、于两点,连接、、,下列结论:①;②;;④. 正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(本大题共6小题,每小题4分,共24分)
13.因式分解: .
14.关于的一元二次方程有两个实数根,则的取值范围是 .
15.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地. ,斜坡长,斜坡的坡比为. 为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造. 经地质人员勘测,当坡角不超过时,可确保山体不滑坡,如果改造时保持坡脚不动,则坡顶沿至少向右移 时,才能确保山体不滑坡. (取)
16.如图,在中,是边上一点,按以下步骤作图:①以点为圆心,以适当长为半径作弧,分别交,于点;②以点为圆心,以长为半径作弧,交于点;③以点为圆心,以长为半径作弧,在内部交前面的弧于点;④过点作射线交于点,若与四边形的面积比为,则的值为 .
17.若关于的方程的解是正数,则的取值范围为 .
18.如图,在平面直角坐标系中,边长为2的正方形的两边在坐标轴上,以它的对角线,为边作正方形,再以正方形的对角线为边作正方形以此类推,则正方形的顶点的坐标是 .
三、解答题(本大题共8个小题,共78分)
19.(8分)计算:.
20.(8分)解不等式组,并将解集在数轴上出来.
21.(10分)为提高学生的安全意识,某学校组织学生参加了“安全知识答题”活动. 该校随机抽取部分学生答题成绩进行统计,将成绩分为四个等级:(优秀),(良好),(一般),(不合格),并根据结果绘制成如图所示的两幅不完整的统计图.
根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取 人,条形统计图中的 ;
(2)将条形统计图补充完整,在扇形统计图中,求等所在扇形圆心角的度数;
(3)该校有1200名学生,估计该校学生答题成绩为等和等共有多少人;
(4)学校要从答题成绩为等且表达能力较强的甲、乙、丙、丁四名学生中,随机抽出两名学生去做“安全知识宣传员”,请用列表或画树状图的方法,求抽出的两名学生恰好是甲和丁的概率.
22.(10分)如图,是的直径,过圆上点的直线交延长线于点,且.
(1)求证:是的切线;
(2)若,求的长.
23.(10分)某校开设智能机器人编程的校本课程,购买了,两种型号的机器人模型. 型机器人模型单价比型机器人模型单价多200元,用2000元购买型机器人模型和用1200元购买型机器人模型的数量相同.
(1)求型,型机器人模型的单价分别是多少元?
(2)学校准备再次购买型和型机器人模型共40台,购买型机器人模型不超过型机器人模型的3倍,且商家给出了两种型号机器人模型均打八折的优惠. 问购买型和型机器人模型各多少台时花费最少?最少花费是多少元?
24.(10分)如图,一次函数的图象与反比例函数的图象交于点. 将点沿轴正方向平移个单位长度得到点,为轴正半轴上的点,点的横坐标大于点的横坐标,连接,的中点在反比例函数的图象上.
(1)求的值;
(2)当为何值时,的值最大?最大值是多少?
25.(10分)如图,在菱形中,,为对角线. 点是边延长线上的任意点,连结交于点,平分交于点.
(1)求证:.
(2)若. 求菱形的面积与的值.
26.(12分)已知抛物线与轴相交于点,与轴相交于点.
(1)求抛物线的表达式;
(2)如图1,点是抛物线的对称轴上的一个动点,当的周长最小时,求的值:
(3)如图2,取线段的中点,在抛物线上是否存在点2,使?若存在,求出点的坐标;若不存在,请说明理由。
九年级(下)数学试题 2024.4
考试时间 120分钟 总分 150分
一、选择题(本大题共12个小题,每小题4分,共48分)
1.下列实数:,其中最小的是( )
A. B.0 C. D.
2.2022年12月31日,仁寿县户籍人口为150.13万人. 其中数据150.13万用科学记数法表示为( )
A. B. C. D.
3.下面计算正确的是( )
A. B. C. D.
4.如图,直线,且于点,若,则的度数为( )
A. B. C. D.
5.如图是由一个长方体和一个圆柱组成的几何体,它的俯视图是 ( )
A. B. C. D.
6.为了解学生的身体素质状况,国家每年都会进行中小学生身体素质抽测. 在今年的抽测中,某校九年级二班随机抽取了10名男生进行引体向上测试,他们的成绩(单位:个)如下:7,11,10,11,6,14,11,10,11,9. 根据这组数据判断下列结论中错误的是( )
A.这组数据的众数是11 B.这组数据的中位数是10
C.这组数据的平均数是10 D.这组数据的方差是4.6
7.《九章算术》中记载了一种测量井深的方法. 如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸,视线与井口的直径交于点,如果测得米,米,米,那么井深为( )米.
A.7.5 B.7 C.6.5 D.6
8.关于的一次函数,若随的增大而增大,且图象与轴的交点在原点下方,则实数的取值范围是( )
A. B. C. D.
9.已知,是方程的两个实数根,则式子的值为( )
A.1 B. C.3 D.
10.如图,四边形的顶点,,都在上,,则的弧长为 ( )
A. B. C. D.
11.对称轴为直线的抛物线(,,为常数,且)如图所示,小明同学得出了以下结论:①,②,③,④,⑤(为任意实数),⑥当时,随的增大而减小.
其中结论正确的个数为( )
A.3 B.4 C.5 D.6
12.在正方形中,,点是边的中点,连接,延长至点,使得,过点作,分别交、于两点,连接、、,下列结论:①;②;;④. 正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(本大题共6小题,每小题4分,共24分)
13.因式分解: .
14.关于的一元二次方程有两个实数根,则的取值范围是 .
15.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地. ,斜坡长,斜坡的坡比为. 为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造. 经地质人员勘测,当坡角不超过时,可确保山体不滑坡,如果改造时保持坡脚不动,则坡顶沿至少向右移 时,才能确保山体不滑坡. (取)
16.如图,在中,是边上一点,按以下步骤作图:①以点为圆心,以适当长为半径作弧,分别交,于点;②以点为圆心,以长为半径作弧,交于点;③以点为圆心,以长为半径作弧,在内部交前面的弧于点;④过点作射线交于点,若与四边形的面积比为,则的值为 .
17.若关于的方程的解是正数,则的取值范围为 .
18.如图,在平面直角坐标系中,边长为2的正方形的两边在坐标轴上,以它的对角线,为边作正方形,再以正方形的对角线为边作正方形以此类推,则正方形的顶点的坐标是 .
三、解答题(本大题共8个小题,共78分)
19.(8分)计算:.
20.(8分)解不等式组,并将解集在数轴上出来.
21.(10分)为提高学生的安全意识,某学校组织学生参加了“安全知识答题”活动. 该校随机抽取部分学生答题成绩进行统计,将成绩分为四个等级:(优秀),(良好),(一般),(不合格),并根据结果绘制成如图所示的两幅不完整的统计图.
根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取 人,条形统计图中的 ;
(2)将条形统计图补充完整,在扇形统计图中,求等所在扇形圆心角的度数;
(3)该校有1200名学生,估计该校学生答题成绩为等和等共有多少人;
(4)学校要从答题成绩为等且表达能力较强的甲、乙、丙、丁四名学生中,随机抽出两名学生去做“安全知识宣传员”,请用列表或画树状图的方法,求抽出的两名学生恰好是甲和丁的概率.
22.(10分)如图,是的直径,过圆上点的直线交延长线于点,且.
(1)求证:是的切线;
(2)若,求的长.
23.(10分)某校开设智能机器人编程的校本课程,购买了,两种型号的机器人模型. 型机器人模型单价比型机器人模型单价多200元,用2000元购买型机器人模型和用1200元购买型机器人模型的数量相同.
(1)求型,型机器人模型的单价分别是多少元?
(2)学校准备再次购买型和型机器人模型共40台,购买型机器人模型不超过型机器人模型的3倍,且商家给出了两种型号机器人模型均打八折的优惠. 问购买型和型机器人模型各多少台时花费最少?最少花费是多少元?
24.(10分)如图,一次函数的图象与反比例函数的图象交于点. 将点沿轴正方向平移个单位长度得到点,为轴正半轴上的点,点的横坐标大于点的横坐标,连接,的中点在反比例函数的图象上.
(1)求的值;
(2)当为何值时,的值最大?最大值是多少?
25.(10分)如图,在菱形中,,为对角线. 点是边延长线上的任意点,连结交于点,平分交于点.
(1)求证:.
(2)若. 求菱形的面积与的值.
26.(12分)已知抛物线与轴相交于点,与轴相交于点.
(1)求抛物线的表达式;
(2)如图1,点是抛物线的对称轴上的一个动点,当的周长最小时,求的值:
(3)如图2,取线段的中点,在抛物线上是否存在点2,使?若存在,求出点的坐标;若不存在,请说明理由。
同课章节目录
