【多媒体导学案】人教版数学九年级上册第23章第2课时《图形旋转的性质》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第23章第2课时《图形旋转的性质》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 296.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-14 00:00:00 | ||
图片预览


文档简介
一、学习目标 1.旋转的基本性质;2.利用旋转的基本性质解决相关问题。
二、知识回顾 1.旋转的定义:在同一个平面内,把一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转。2.旋转的三要素: 旋转中心、旋转方向、旋转角度 .旋转角是 对应点 与 旋转中心 所连线段的夹角。
三、新知讲解 1.旋转的性质①对应点到旋转中心的距离 相等 。② 对应点与旋转中心所连线段的夹角 等于旋转角。③旋转前、后的图形 全等 ,所以对应边相等,对应角相等.2.旋转作图图形在旋转作图时,部分与整体是同步的,在旋转作图时,关键是作出图形上的关键点旋转后的对应点。(1)旋转作图的依据:旋转图形的旋转角都相等,对应点到旋转中心的距离相等。(2)旋转作图的一般步骤:①分析题目要求,找出旋转中心、旋转方向和旋转角。②分析所要旋转的图形,找出构成图形的关键点。③按一定的方向和一定的角度,通过截取线段的方法,旋转各关键点,作出各关键点的对应点。④顺次连接所得到的各点,并标上相应的字母。
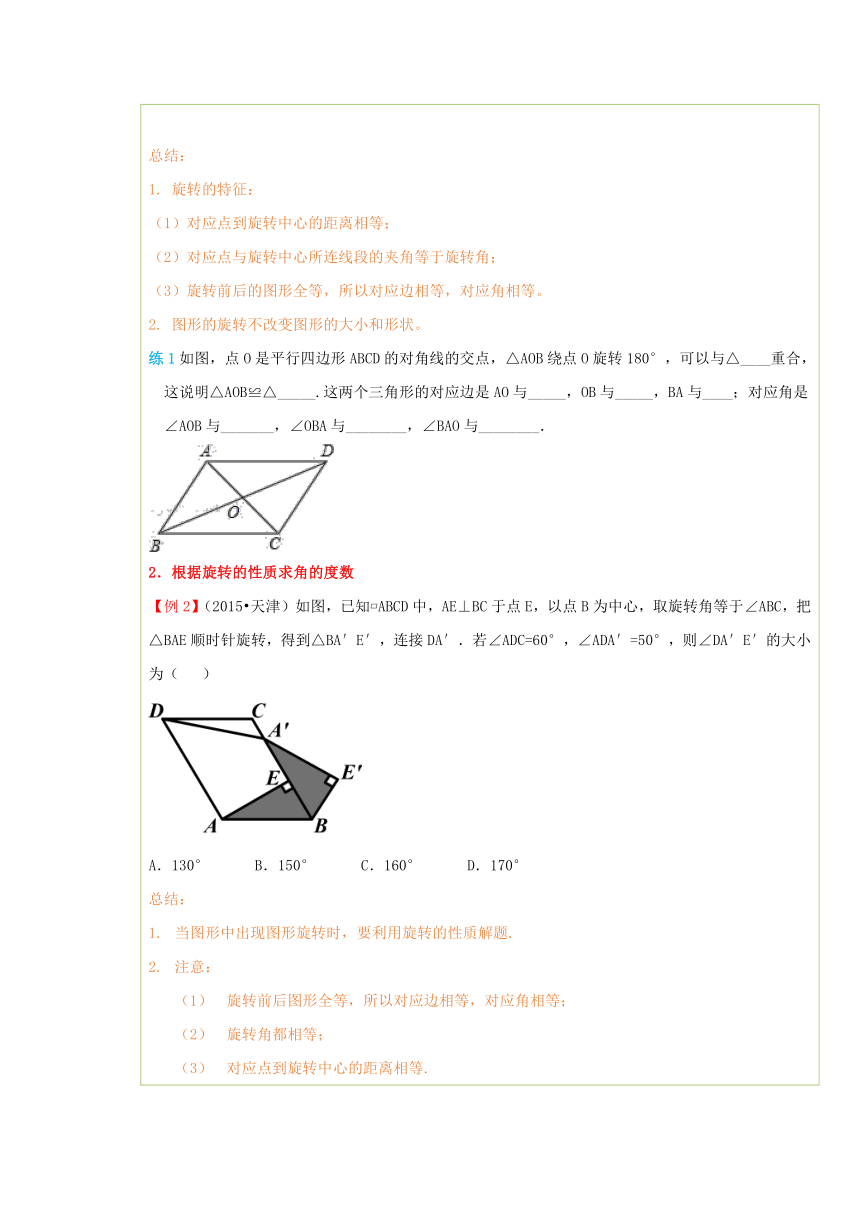
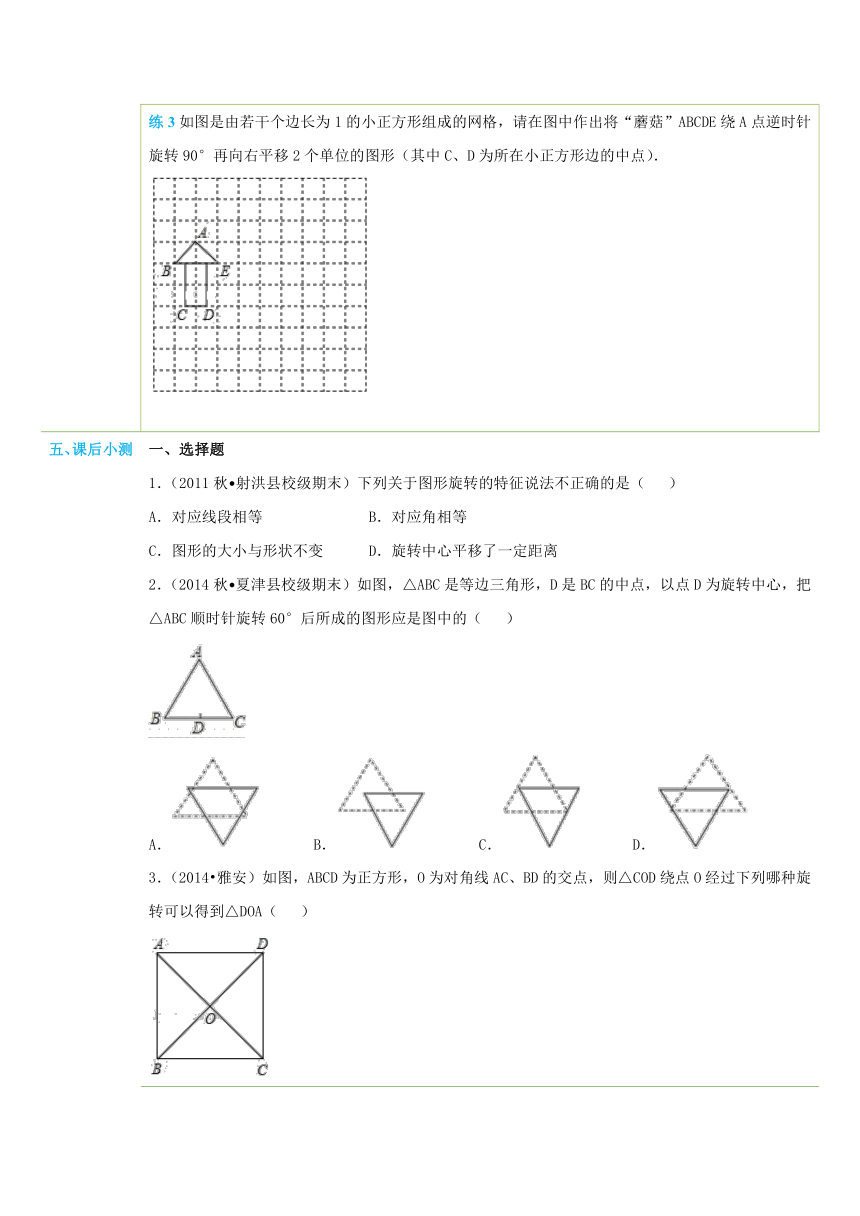
四、典例探究 扫一扫,有惊喜哦!1.根据旋转的性质找相等的线段或角【例1】如图,若把△ABC绕点A旋转一定 ( http: / / www.21cnjy.com )角度就得到△ADE,那么AB=______,BC=______,∠CAB=______,∠B=_______. ( http: / / www.21cnjy.com )总结:1. 旋转的特征:(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前后的图形全等,所以对应边相等,对应角相等。2. 图形的旋转不改变图形的大小和形状。练1如图,点O是平行四边形ABCD的对角线 ( http: / / www.21cnjy.com )的交点,△AOB绕点O旋转180°,可以与△____重合,这说明△AOB≌△_____.这两个三角形的对应边是AO与_____,OB与_____,BA与____;对应角是∠AOB与_______,∠OBA与________,∠BAO与________. ( http: / / www.21cnjy.com )2.根据旋转的性质求角的度数【例2】(2015 天津)如图,已知 AB ( http: / / www.21cnjy.com )CD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( ) ( http: / / www.21cnjy.com )A.130° B.150° C.160° D.170°总结:当图形中出现图形旋转时,要利用旋转的性质解题.注意:旋转前后图形全等,所以对应边相等,对应角相等;旋转角都相等;对应点到旋转中心的距离相等.练2(2010春 姜堰市校级期中)如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°. ( http: / / www.21cnjy.com )(1)请说明∠EAB=∠FAC的理由;(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;(3)求∠AMB的度数.3.已知一个图形和旋转中心,画旋转图形【例3】在如图所示的方格纸 ( http: / / www.21cnjy.com )中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC绕点O逆时针旋转90°后的△A′B′C′. ( http: / / www.21cnjy.com )总结:旋转作图的基本步骤:(1)根据题意,确定旋转中心、旋转方向和旋转角;(2)找出原图形的关键点;(3)连接各关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到这些关键点的对应点,并标上相应的字母;(4)按原图形依次连接这些对应点,得到旋转后的图形。练3如图是由若干个边长为1的小正方形组 ( http: / / www.21cnjy.com )成的网格,请在图中作出将“蘑菇”ABCDE绕A点逆时针旋转90°再向右平移2个单位的图形(其中C、D为所在小正方形边的中点). ( http: / / www.21cnjy.com )
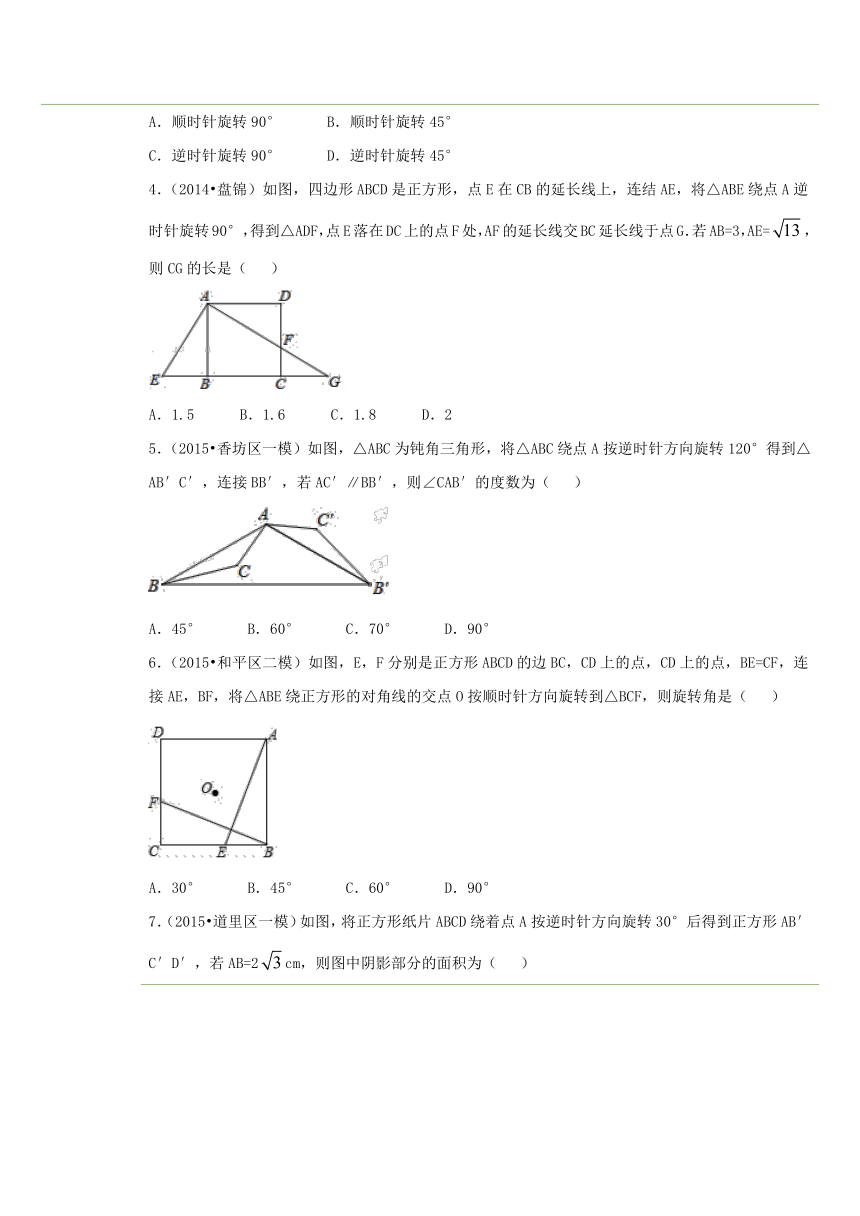
五、课后小测 一、选择题1.(2011秋 射洪县校级期末)下列关于图形旋转的特征说法不正确的是( )A.对应线段相等 B.对应角相等C.图形的大小与形状不变 D.旋转中心平移了一定距离2.(2014秋 夏津县校级期末) ( http: / / www.21cnjy.com )如图,△ABC是等边三角形,D是BC的中点,以点D为旋转中心,把△ABC顺时针旋转60°后所成的图形应是图中的( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )3.(2014 雅安)如图,ABCD为正方形,O为对角线AC、BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA( ) ( http: / / www.21cnjy.com )A.顺时针旋转90° B.顺时针旋转45°C.逆时针旋转90° D.逆时针旋转45°4.(2014 盘锦)如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=,则CG的长是( ) ( http: / / www.21cnjy.com )A.1.5 B.1.6 C.1.8 D.25.(2015 香坊区一模)如图, ( http: / / www.21cnjy.com )△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( ) ( http: / / www.21cnjy.com )A.45° B.60° C.70° D.90°6.(2015 和平区二模)如图,E,F分别 ( http: / / www.21cnjy.com )是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( ) ( http: / / www.21cnjy.com )A.30° B.45° C.60° D.90°7.(2015 道里区一模)如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2cm,则图中阴影部分的面积为( ) ( http: / / www.21cnjy.com )A.6cm2 B.(12﹣6)cm2 C.3cm2 D.4cm28.(2015 哈尔滨)如 ( http: / / www.21cnjy.com )图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( ) ( http: / / www.21cnjy.com )A.32° B.64° C.77° D.87°二、填空题9.(2014秋 乌海期 ( http: / / www.21cnjy.com )末)如图,下面的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2,∠AOB为120°,则图中阴影部分的面积之和为_______cm2. ( http: / / www.21cnjy.com )10.(2014秋 盈江县校级期中)如 ( http: / / www.21cnjy.com )图,若把△ABC绕A点顺时针旋转一定角度,就得到△ADE,请写出图中所有的对应边是_____________,对应角是_______________. ( http: / / www.21cnjy.com )三、解答题11.(2012 仁寿县校级模拟)如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′,再绕O′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(﹣2,3),B点坐标为(﹣3,0). ( http: / / www.21cnjy.com )①在图中画△A′B′O′和△A″B″O″;②直接写出A′和A″点的坐标;③△ABO的顶点A在变换过程中所经过的路径长为多少?12.(2009秋 宜城市期末)在正方 ( http: / / www.21cnjy.com )形ABCD中,点E在BC上,点F在AB上,∠FDE=45°,△DEC按顺时针方向旋转一个角度后成△DGA,如下图所示.(1)哪一个点是旋转中心旋转角度等于多少?(2)指出图中的对应线段和对应角;(3)求∠GDF的度数. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据旋转的性质、结合图形得出即可.
解:∵把△ABC绕点A旋转一定角度就得到△ADE,
∴△ACB≌△AED,
∴AB=AD,BC=DE,∠CAB=∠EAD,∠B=∠D,
故答案为:AD,DE,∠EAD,∠D.
点评:本题考查了旋转的性质的应用,注意:旋转后得出的图形和原图形全等.
练1.【解析】在平行四边形ABCD ( http: / / www.21cnjy.com )中,点O为对角线的交点,所以△AOB绕O旋转180°,则与△COD重合,即△AOB≌△COD,进而可求解结论.
解:由题中条件可得△AOB≌△COD,
∴OA=OC,OB=OD,BA=CD,∠AOB=∠COD,∠OBA=∠ODC,∠BAO=∠OCD.
故此题答案为COD,COD,OC,OD,CD,∠COD,∠ODC,∠OCD.
点评:本题主要考查了全等三角形的判定及性质问题,能够熟练掌握.
【例2】【解析】根据平行四边形对角相等, ( http: / / www.21cnjy.com )得∠ABC=60°,再由平行线的性质求出∠DA′B=130°,最后根据旋转的性质得到∠BA′E′=∠BAE=30°,从而得到答案.
解:∵四边形ABCD是平行四边形,∠ADC=60°,
∴∠ABC=60°,
∵AD//BC,∠ADA′=50°,
∴∠DA′B=130°,
∵AE⊥BC于点E,
∴∠BAE=30°,
∵△BAE顺时针旋转,得到△BA′E′,
∴∠BA′E′=∠BAE=30°,
∴∠DA′E′=∠DA′B+∠BA′E′=160°.
故选:C.
点评:本题主要考查了平行四边形的性质,旋转的性质,此题难度不大,关键是能综合运用以上知识点求出∠DA′B和∠BA′E′.
练2.【解析】(1)先利用已知条件∠ ( http: / / www.21cnjy.com )B=∠E,AB=AE,BC=EF,利用SAS可证△ABC≌△AEF,那么就有∠C=∠F,∠BAC=∠EAF,那么∠BAC﹣∠PAF=∠EAF﹣∠PAF,即有∠BAE=∠CAF=25°;
(2)通过观察可知△ABC绕点A顺时针旋转25°,可以得到△AEF;
(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=25°,而∠AMB是△ACM的外角,根据三角形外角的性质可求∠AMB.
解:(1)∵∠B=∠E,AB=AE,BC=EF,
∴△ABC≌△AEF,
∴∠C=∠F,∠BAC=∠EAF,
∴∠BAC﹣∠PAF=∠EAF﹣∠PAF,
∴∠BAE=∠CAF=25°;
(2)通过观察可知△ABC绕点A顺时针旋转25°,可以得到△AEF;
(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=25°,
∴∠AMB=∠C+∠CAF=57°+25°=82°.
点评:本题利用了全等三角形的判定、性质,三角形外角的性质,等式的性质等.
【例3】【解析】本题是在网格中将△AB ( http: / / www.21cnjy.com )C绕点O逆时针旋转90°,画图时,除了把握好旋转方向外,还要确保OA=OA′,OA⊥OA′,OB=OB′,OB⊥OB′,OC=OC′,OC⊥OC′.
解: ( http: / / www.21cnjy.com )
点评:本题难度中等,考查网格中 ( http: / / www.21cnjy.com )的旋转作图,作图时,抓住网格的特点,根据旋转的性质,借助于直角三角板中的直角,就能顺利作出图形,解题时要注意是顺时针方向还是逆时针方向.
练3.【解析】本题主要是根据旋转的性质画图.即对应点旋转的角度相行,线段相等,然后再平移2个单元格即可
解:
( http: / / www.21cnjy.com )
点评:本题考查旋转变换作图,做这类题的关键是掌握平移旋转的性质。
课后小测答案:
一、选择题
1.【解析】根据旋转的定义和性质进行判断.
解:旋转前后两图形全等,则对应线段相等 ( http: / / www.21cnjy.com ),对应角相等;对应点到旋转中心的距离相等;旋转中心为固定的点,所以A、B、C的说法正确,D的说法错误.
故选:D.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
2.【解析】根据等边三角形的性质得∠B=∠ ( http: / / www.21cnjy.com )ACB=60°,再利用旋转的性质得∠A′B′C′=60°,∠BDB′=60°,DB=DB′,△BDB′为等边三角形,点B′在AB上,同理可得点C在A′C′上,则可画出图形,然后进行判断.
解:∵△ABC是等边三角形,
∴∠B=∠ACB=60°,
∵以点D为旋转中心,把△ABC顺时针旋转60°得到△A′B′C′,而D是BC的中点,
∴∠A′B′C′=60°,∠BDB′=60°,DB=DB′,
∴点B′在AB上,
同理可得点C在A′C′上,如图.
故选:C.
( http: / / www.21cnjy.com )
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
3.【解析】因为四边形ABC ( http: / / www.21cnjy.com )D为正方形,所以∠COD=∠DOA=90°,OC=OD=OA,则△COD绕点O逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,据此可得答案.
解:∵四边形ABCD为正方形,
∴∠COD=∠DOA=90°,OC=OD=OA,
∴△COD绕点O逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,
故选:C.
点评:本题考查了旋转的性质,旋转要找出旋转中心、旋转方向、旋转角.
4.【解析】先根据正方形的性质得AB=AD=CD=3,再根据旋转的性质得AF=AE=,则可根据勾股定理计算出DF=2,所以CF=CD﹣DF=1,然后证明△CGF∽△DAF,再利用相似比可计算出CG.
解:∵四边形ABCD是正方形,
∴AB=AD=CD=3,
∵△ABE绕点A逆时针旋转90°,得到△ADF,
∴AF=AE=,
在Rt△ADF中,∵AD=3,AF=,
∴DF=,
∴CF=CD﹣DF=3﹣2=1,
∵AD∥CG,
∴△CGF∽△DAF,
∴,即,
∴CG=1.5.
故选A.
点评:本题考查了旋转的性质:对应点到旋 ( http: / / www.21cnjy.com )转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和相似三角形的判定与性质.
5.【解析】先根据旋转的性质得到∠BA ( http: / / www.21cnjy.com )B′=∠CAC′=120°,AB=AB′,根据等腰三角形的性质易得∠AB′B=30°,再根据平行线的性质由AC′∥BB′得∠C′AB′=∠AB′B=30°,然后利用∠CAB′=∠CAC′﹣∠C′AB′进行计算.
解:∵将△ABC绕点A按逆时针方向旋转l20°得到△AB′C′,
∴∠BAB′=∠CAC′=120°,AB=AB′,
∴∠AB′B=(180°﹣120°)=30°,
∵AC′∥BB′,
∴∠C′AB′=∠AB′B=30°,
∴∠CAB′=∠CAC′﹣∠C′AB′=120°﹣30°=90°.
故选:D.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
6.【解析】根据旋转性质得出旋转后A到B,只要根据正方形的性质和三角形的内角和定理求出∠AOB即可.
解:将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF时,A和B重合,
即∠AOB是旋转角,
∵四边形ABCD是正方形,
∴∠BAO=∠ABO=45°,
∴∠AOB=180°﹣45°﹣45°=90°,
即旋转角是90°.
故选:D.
( http: / / www.21cnjy.com )
点评:本题考查了旋转的性质和正方形性质,主要考查学生的理解能力和推理能力,关键是找到旋转角.
7.【解析】设CD,B′C′相交于点M,DM=x,则∠MAD=30°,AM=2x,x2+(2)2=4x2,解得x=2,所以重叠部分的面积SADMB′=2S△ADM.
解:设CD,B′C′相交于点M,DM=x,则∠MAD=30° AM=2x,
∵x2++(2)2=4x2,
∴x=2,
∴S△ADM= AD DM=×2×2=2,
∴重叠部分的面积SADMB′=4.
故选:D.
( http: / / www.21cnjy.com )
点评:本题考查旋转的性质.旋转变化前后, ( http: / / www.21cnjy.com )对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
8.【解析】旋转中心为点A,C、C′为对应点 ( http: / / www.21cnjy.com ),可知AC=AC′,又因为∠CAC′=90°,根据三角形外角的性质求出∠C′B′A的度数,进而求出∠B的度数.
解:由旋转的性质可知,AC=AC′,
∵∠CAC′=90°,可知△CAC′为等腰直角三角形,则∠CC′A=45°.
∵∠CC′B′=32°,
∴∠C′B′A=∠C′CA+∠CC′B′=45°+32°=77°,
∵∠B=∠C′B′A,
∴∠B=77°,
故选:C.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应角相等,对应线段相等.也考查了等腰直角三角形的性质.
二、填空题
9.【解析】根据旋转的性质和图形的特点解答.
解:每个叶片的面积为4cm2,因而图形的面积是12cm2,
∵图案绕点O旋转120°后可以和自身重合,∠AOB为120°
∴图形中阴影部分的面积是图形的面积的,
因而图中阴影部分的面积之和为4cm2.
故答案为4.
点评:本题考查了图形的旋转与重合,理 ( http: / / www.21cnjy.com )解旋转对称图形的定义是解决本题的关键.注:旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
10.【解析】根据旋转前后相等的边是对应边,相等的角是对应角即可得到答案.
解:∵△ABC绕A点顺时针旋转一定角度,就得到△ADE,
∴△ABC≌△ADE,
∴对应边为:AB和AD,AC和AE,BC和DE,对应角为:∠BAC和∠EAD,∠B和∠D,∠C和∠E,
故答案为:AB和AD,AC和AE,BC和DE;∠BAC和∠EAD,∠B和∠D,∠C和∠E.
点评:本题主要考查旋转的性质,掌握旋转前后两个图形是全等形是解题的关键.
三、解答题
11.【解析】①根据网格结构找出平移与旋转变换后的对应点的位置,然后顺次连接即可;
②根据平面直角坐标系写出点A′和A″的坐标即可;
③根据勾股定理列式求出O′A′的长度,再根据弧长公式求出A′旋转的路径长,然后加上平移的距离即可得解.
解:①△A′B′O′和△A″B″O″如图所示;
②A′(2,3)、A″(7,2);
③根据勾股定理,O′A′=,
所以,弧A′A″的长度=,
又∵△ABC沿x轴的正方向平移4单位得到△A′B′O′,
∴点A在变换过程中所经过的路径长=4+π.
( http: / / www.21cnjy.com )
点评:本题考查了利用旋转变换作图,利用平移变换作图,以及弧长的计算,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
12.【解析】由已知:△DEC按顺时针方向旋转一个角度后成△DGA,观察对应边可得,旋转中心是D点,旋转角为90°;
根据旋转的性质可以得到△DEC≌△DGA,则∠GDA=∠EDC,据此即可求得∠GDF的度数.
解:(1)D点是旋转中心,旋转角是90°.
(2)对应线段是DE和DG,DC和DA,CE和AG.
对应角是∠CDE和∠ADG,∠C和∠DAG,∠DEC和∠G.
(3)∵∠FDE=45°,∠ADC=90°,
∴∠ADF+∠EDC=90°﹣45°=45°,
∵∠GDF=∠GDA+∠ADF,∠GDA=∠EDC,
∴∠GDF=∠EDC+∠ADF=45°.
点评:本题考查旋转的性质﹣﹣旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
二、知识回顾 1.旋转的定义:在同一个平面内,把一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转。2.旋转的三要素: 旋转中心、旋转方向、旋转角度 .旋转角是 对应点 与 旋转中心 所连线段的夹角。
三、新知讲解 1.旋转的性质①对应点到旋转中心的距离 相等 。② 对应点与旋转中心所连线段的夹角 等于旋转角。③旋转前、后的图形 全等 ,所以对应边相等,对应角相等.2.旋转作图图形在旋转作图时,部分与整体是同步的,在旋转作图时,关键是作出图形上的关键点旋转后的对应点。(1)旋转作图的依据:旋转图形的旋转角都相等,对应点到旋转中心的距离相等。(2)旋转作图的一般步骤:①分析题目要求,找出旋转中心、旋转方向和旋转角。②分析所要旋转的图形,找出构成图形的关键点。③按一定的方向和一定的角度,通过截取线段的方法,旋转各关键点,作出各关键点的对应点。④顺次连接所得到的各点,并标上相应的字母。
四、典例探究 扫一扫,有惊喜哦!1.根据旋转的性质找相等的线段或角【例1】如图,若把△ABC绕点A旋转一定 ( http: / / www.21cnjy.com )角度就得到△ADE,那么AB=______,BC=______,∠CAB=______,∠B=_______. ( http: / / www.21cnjy.com )总结:1. 旋转的特征:(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前后的图形全等,所以对应边相等,对应角相等。2. 图形的旋转不改变图形的大小和形状。练1如图,点O是平行四边形ABCD的对角线 ( http: / / www.21cnjy.com )的交点,△AOB绕点O旋转180°,可以与△____重合,这说明△AOB≌△_____.这两个三角形的对应边是AO与_____,OB与_____,BA与____;对应角是∠AOB与_______,∠OBA与________,∠BAO与________. ( http: / / www.21cnjy.com )2.根据旋转的性质求角的度数【例2】(2015 天津)如图,已知 AB ( http: / / www.21cnjy.com )CD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( ) ( http: / / www.21cnjy.com )A.130° B.150° C.160° D.170°总结:当图形中出现图形旋转时,要利用旋转的性质解题.注意:旋转前后图形全等,所以对应边相等,对应角相等;旋转角都相等;对应点到旋转中心的距离相等.练2(2010春 姜堰市校级期中)如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°. ( http: / / www.21cnjy.com )(1)请说明∠EAB=∠FAC的理由;(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;(3)求∠AMB的度数.3.已知一个图形和旋转中心,画旋转图形【例3】在如图所示的方格纸 ( http: / / www.21cnjy.com )中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC绕点O逆时针旋转90°后的△A′B′C′. ( http: / / www.21cnjy.com )总结:旋转作图的基本步骤:(1)根据题意,确定旋转中心、旋转方向和旋转角;(2)找出原图形的关键点;(3)连接各关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到这些关键点的对应点,并标上相应的字母;(4)按原图形依次连接这些对应点,得到旋转后的图形。练3如图是由若干个边长为1的小正方形组 ( http: / / www.21cnjy.com )成的网格,请在图中作出将“蘑菇”ABCDE绕A点逆时针旋转90°再向右平移2个单位的图形(其中C、D为所在小正方形边的中点). ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2011秋 射洪县校级期末)下列关于图形旋转的特征说法不正确的是( )A.对应线段相等 B.对应角相等C.图形的大小与形状不变 D.旋转中心平移了一定距离2.(2014秋 夏津县校级期末) ( http: / / www.21cnjy.com )如图,△ABC是等边三角形,D是BC的中点,以点D为旋转中心,把△ABC顺时针旋转60°后所成的图形应是图中的( ) ( http: / / www.21cnjy.com )A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )3.(2014 雅安)如图,ABCD为正方形,O为对角线AC、BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA( ) ( http: / / www.21cnjy.com )A.顺时针旋转90° B.顺时针旋转45°C.逆时针旋转90° D.逆时针旋转45°4.(2014 盘锦)如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=,则CG的长是( ) ( http: / / www.21cnjy.com )A.1.5 B.1.6 C.1.8 D.25.(2015 香坊区一模)如图, ( http: / / www.21cnjy.com )△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( ) ( http: / / www.21cnjy.com )A.45° B.60° C.70° D.90°6.(2015 和平区二模)如图,E,F分别 ( http: / / www.21cnjy.com )是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( ) ( http: / / www.21cnjy.com )A.30° B.45° C.60° D.90°7.(2015 道里区一模)如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2cm,则图中阴影部分的面积为( ) ( http: / / www.21cnjy.com )A.6cm2 B.(12﹣6)cm2 C.3cm2 D.4cm28.(2015 哈尔滨)如 ( http: / / www.21cnjy.com )图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( ) ( http: / / www.21cnjy.com )A.32° B.64° C.77° D.87°二、填空题9.(2014秋 乌海期 ( http: / / www.21cnjy.com )末)如图,下面的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2,∠AOB为120°,则图中阴影部分的面积之和为_______cm2. ( http: / / www.21cnjy.com )10.(2014秋 盈江县校级期中)如 ( http: / / www.21cnjy.com )图,若把△ABC绕A点顺时针旋转一定角度,就得到△ADE,请写出图中所有的对应边是_____________,对应角是_______________. ( http: / / www.21cnjy.com )三、解答题11.(2012 仁寿县校级模拟)如图将△ABC沿x轴的正方向平移4单位得到△A′B′O′,再绕O′点按顺时针旋转90°得到△A″B″O″,若A的坐标为(﹣2,3),B点坐标为(﹣3,0). ( http: / / www.21cnjy.com )①在图中画△A′B′O′和△A″B″O″;②直接写出A′和A″点的坐标;③△ABO的顶点A在变换过程中所经过的路径长为多少?12.(2009秋 宜城市期末)在正方 ( http: / / www.21cnjy.com )形ABCD中,点E在BC上,点F在AB上,∠FDE=45°,△DEC按顺时针方向旋转一个角度后成△DGA,如下图所示.(1)哪一个点是旋转中心旋转角度等于多少?(2)指出图中的对应线段和对应角;(3)求∠GDF的度数. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据旋转的性质、结合图形得出即可.
解:∵把△ABC绕点A旋转一定角度就得到△ADE,
∴△ACB≌△AED,
∴AB=AD,BC=DE,∠CAB=∠EAD,∠B=∠D,
故答案为:AD,DE,∠EAD,∠D.
点评:本题考查了旋转的性质的应用,注意:旋转后得出的图形和原图形全等.
练1.【解析】在平行四边形ABCD ( http: / / www.21cnjy.com )中,点O为对角线的交点,所以△AOB绕O旋转180°,则与△COD重合,即△AOB≌△COD,进而可求解结论.
解:由题中条件可得△AOB≌△COD,
∴OA=OC,OB=OD,BA=CD,∠AOB=∠COD,∠OBA=∠ODC,∠BAO=∠OCD.
故此题答案为COD,COD,OC,OD,CD,∠COD,∠ODC,∠OCD.
点评:本题主要考查了全等三角形的判定及性质问题,能够熟练掌握.
【例2】【解析】根据平行四边形对角相等, ( http: / / www.21cnjy.com )得∠ABC=60°,再由平行线的性质求出∠DA′B=130°,最后根据旋转的性质得到∠BA′E′=∠BAE=30°,从而得到答案.
解:∵四边形ABCD是平行四边形,∠ADC=60°,
∴∠ABC=60°,
∵AD//BC,∠ADA′=50°,
∴∠DA′B=130°,
∵AE⊥BC于点E,
∴∠BAE=30°,
∵△BAE顺时针旋转,得到△BA′E′,
∴∠BA′E′=∠BAE=30°,
∴∠DA′E′=∠DA′B+∠BA′E′=160°.
故选:C.
点评:本题主要考查了平行四边形的性质,旋转的性质,此题难度不大,关键是能综合运用以上知识点求出∠DA′B和∠BA′E′.
练2.【解析】(1)先利用已知条件∠ ( http: / / www.21cnjy.com )B=∠E,AB=AE,BC=EF,利用SAS可证△ABC≌△AEF,那么就有∠C=∠F,∠BAC=∠EAF,那么∠BAC﹣∠PAF=∠EAF﹣∠PAF,即有∠BAE=∠CAF=25°;
(2)通过观察可知△ABC绕点A顺时针旋转25°,可以得到△AEF;
(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=25°,而∠AMB是△ACM的外角,根据三角形外角的性质可求∠AMB.
解:(1)∵∠B=∠E,AB=AE,BC=EF,
∴△ABC≌△AEF,
∴∠C=∠F,∠BAC=∠EAF,
∴∠BAC﹣∠PAF=∠EAF﹣∠PAF,
∴∠BAE=∠CAF=25°;
(2)通过观察可知△ABC绕点A顺时针旋转25°,可以得到△AEF;
(3)由(1)知∠C=∠F=57°,∠BAE=∠CAF=25°,
∴∠AMB=∠C+∠CAF=57°+25°=82°.
点评:本题利用了全等三角形的判定、性质,三角形外角的性质,等式的性质等.
【例3】【解析】本题是在网格中将△AB ( http: / / www.21cnjy.com )C绕点O逆时针旋转90°,画图时,除了把握好旋转方向外,还要确保OA=OA′,OA⊥OA′,OB=OB′,OB⊥OB′,OC=OC′,OC⊥OC′.
解: ( http: / / www.21cnjy.com )
点评:本题难度中等,考查网格中 ( http: / / www.21cnjy.com )的旋转作图,作图时,抓住网格的特点,根据旋转的性质,借助于直角三角板中的直角,就能顺利作出图形,解题时要注意是顺时针方向还是逆时针方向.
练3.【解析】本题主要是根据旋转的性质画图.即对应点旋转的角度相行,线段相等,然后再平移2个单元格即可
解:
( http: / / www.21cnjy.com )
点评:本题考查旋转变换作图,做这类题的关键是掌握平移旋转的性质。
课后小测答案:
一、选择题
1.【解析】根据旋转的定义和性质进行判断.
解:旋转前后两图形全等,则对应线段相等 ( http: / / www.21cnjy.com ),对应角相等;对应点到旋转中心的距离相等;旋转中心为固定的点,所以A、B、C的说法正确,D的说法错误.
故选:D.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
2.【解析】根据等边三角形的性质得∠B=∠ ( http: / / www.21cnjy.com )ACB=60°,再利用旋转的性质得∠A′B′C′=60°,∠BDB′=60°,DB=DB′,△BDB′为等边三角形,点B′在AB上,同理可得点C在A′C′上,则可画出图形,然后进行判断.
解:∵△ABC是等边三角形,
∴∠B=∠ACB=60°,
∵以点D为旋转中心,把△ABC顺时针旋转60°得到△A′B′C′,而D是BC的中点,
∴∠A′B′C′=60°,∠BDB′=60°,DB=DB′,
∴点B′在AB上,
同理可得点C在A′C′上,如图.
故选:C.
( http: / / www.21cnjy.com )
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
3.【解析】因为四边形ABC ( http: / / www.21cnjy.com )D为正方形,所以∠COD=∠DOA=90°,OC=OD=OA,则△COD绕点O逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,据此可得答案.
解:∵四边形ABCD为正方形,
∴∠COD=∠DOA=90°,OC=OD=OA,
∴△COD绕点O逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,
故选:C.
点评:本题考查了旋转的性质,旋转要找出旋转中心、旋转方向、旋转角.
4.【解析】先根据正方形的性质得AB=AD=CD=3,再根据旋转的性质得AF=AE=,则可根据勾股定理计算出DF=2,所以CF=CD﹣DF=1,然后证明△CGF∽△DAF,再利用相似比可计算出CG.
解:∵四边形ABCD是正方形,
∴AB=AD=CD=3,
∵△ABE绕点A逆时针旋转90°,得到△ADF,
∴AF=AE=,
在Rt△ADF中,∵AD=3,AF=,
∴DF=,
∴CF=CD﹣DF=3﹣2=1,
∵AD∥CG,
∴△CGF∽△DAF,
∴,即,
∴CG=1.5.
故选A.
点评:本题考查了旋转的性质:对应点到旋 ( http: / / www.21cnjy.com )转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和相似三角形的判定与性质.
5.【解析】先根据旋转的性质得到∠BA ( http: / / www.21cnjy.com )B′=∠CAC′=120°,AB=AB′,根据等腰三角形的性质易得∠AB′B=30°,再根据平行线的性质由AC′∥BB′得∠C′AB′=∠AB′B=30°,然后利用∠CAB′=∠CAC′﹣∠C′AB′进行计算.
解:∵将△ABC绕点A按逆时针方向旋转l20°得到△AB′C′,
∴∠BAB′=∠CAC′=120°,AB=AB′,
∴∠AB′B=(180°﹣120°)=30°,
∵AC′∥BB′,
∴∠C′AB′=∠AB′B=30°,
∴∠CAB′=∠CAC′﹣∠C′AB′=120°﹣30°=90°.
故选:D.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
6.【解析】根据旋转性质得出旋转后A到B,只要根据正方形的性质和三角形的内角和定理求出∠AOB即可.
解:将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF时,A和B重合,
即∠AOB是旋转角,
∵四边形ABCD是正方形,
∴∠BAO=∠ABO=45°,
∴∠AOB=180°﹣45°﹣45°=90°,
即旋转角是90°.
故选:D.
( http: / / www.21cnjy.com )
点评:本题考查了旋转的性质和正方形性质,主要考查学生的理解能力和推理能力,关键是找到旋转角.
7.【解析】设CD,B′C′相交于点M,DM=x,则∠MAD=30°,AM=2x,x2+(2)2=4x2,解得x=2,所以重叠部分的面积SADMB′=2S△ADM.
解:设CD,B′C′相交于点M,DM=x,则∠MAD=30° AM=2x,
∵x2++(2)2=4x2,
∴x=2,
∴S△ADM= AD DM=×2×2=2,
∴重叠部分的面积SADMB′=4.
故选:D.
( http: / / www.21cnjy.com )
点评:本题考查旋转的性质.旋转变化前后, ( http: / / www.21cnjy.com )对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
8.【解析】旋转中心为点A,C、C′为对应点 ( http: / / www.21cnjy.com ),可知AC=AC′,又因为∠CAC′=90°,根据三角形外角的性质求出∠C′B′A的度数,进而求出∠B的度数.
解:由旋转的性质可知,AC=AC′,
∵∠CAC′=90°,可知△CAC′为等腰直角三角形,则∠CC′A=45°.
∵∠CC′B′=32°,
∴∠C′B′A=∠C′CA+∠CC′B′=45°+32°=77°,
∵∠B=∠C′B′A,
∴∠B=77°,
故选:C.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应角相等,对应线段相等.也考查了等腰直角三角形的性质.
二、填空题
9.【解析】根据旋转的性质和图形的特点解答.
解:每个叶片的面积为4cm2,因而图形的面积是12cm2,
∵图案绕点O旋转120°后可以和自身重合,∠AOB为120°
∴图形中阴影部分的面积是图形的面积的,
因而图中阴影部分的面积之和为4cm2.
故答案为4.
点评:本题考查了图形的旋转与重合,理 ( http: / / www.21cnjy.com )解旋转对称图形的定义是解决本题的关键.注:旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
10.【解析】根据旋转前后相等的边是对应边,相等的角是对应角即可得到答案.
解:∵△ABC绕A点顺时针旋转一定角度,就得到△ADE,
∴△ABC≌△ADE,
∴对应边为:AB和AD,AC和AE,BC和DE,对应角为:∠BAC和∠EAD,∠B和∠D,∠C和∠E,
故答案为:AB和AD,AC和AE,BC和DE;∠BAC和∠EAD,∠B和∠D,∠C和∠E.
点评:本题主要考查旋转的性质,掌握旋转前后两个图形是全等形是解题的关键.
三、解答题
11.【解析】①根据网格结构找出平移与旋转变换后的对应点的位置,然后顺次连接即可;
②根据平面直角坐标系写出点A′和A″的坐标即可;
③根据勾股定理列式求出O′A′的长度,再根据弧长公式求出A′旋转的路径长,然后加上平移的距离即可得解.
解:①△A′B′O′和△A″B″O″如图所示;
②A′(2,3)、A″(7,2);
③根据勾股定理,O′A′=,
所以,弧A′A″的长度=,
又∵△ABC沿x轴的正方向平移4单位得到△A′B′O′,
∴点A在变换过程中所经过的路径长=4+π.
( http: / / www.21cnjy.com )
点评:本题考查了利用旋转变换作图,利用平移变换作图,以及弧长的计算,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
12.【解析】由已知:△DEC按顺时针方向旋转一个角度后成△DGA,观察对应边可得,旋转中心是D点,旋转角为90°;
根据旋转的性质可以得到△DEC≌△DGA,则∠GDA=∠EDC,据此即可求得∠GDF的度数.
解:(1)D点是旋转中心,旋转角是90°.
(2)对应线段是DE和DG,DC和DA,CE和AG.
对应角是∠CDE和∠ADG,∠C和∠DAG,∠DEC和∠G.
(3)∵∠FDE=45°,∠ADC=90°,
∴∠ADF+∠EDC=90°﹣45°=45°,
∵∠GDF=∠GDA+∠ADF,∠GDA=∠EDC,
∴∠GDF=∠EDC+∠ADF=45°.
点评:本题考查旋转的性质﹣﹣旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
同课章节目录
