【多媒体导学案】人教版数学九年级上册第23章第4课时《中心对称及其性质》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第23章第4课时《中心对称及其性质》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 377.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-14 16:44:56 | ||
图片预览


文档简介
一、学习目标 认识两个图形关于某个点中心对称的本质;理解中心对称的性质,并可以判断两个图形是否成中心对称;会画某图形关于某点对称的图形,会确定对称中心;会利用中心对称的性质求长度、角度和面积.
二、知识回顾 1.什么是两个图形成轴对称?成轴对称的两个图形有哪些性质?把一个图形沿着某一条直线折叠能与另一个图形完全重合,那么就说这两个图形关于这条直线对称或成轴对称.性质:成轴对称的两个图形是全等形,对称轴是对称点连线的垂直平分线.2.什么是旋转?旋转的特征是什么?在平面内,将一个图形绕一个定点旋转一定角度,这样的图形变换称为图形的旋转.性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前后的图形全等,对应线段相等,对应角相等.
三、新知讲解 中心对称把一个图形绕着某一个点旋转180°,如果 ( http: / / www.21cnjy.com )它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这个两个图形中的对应点叫做关于对称中心的对称点.中心对称的性质(1)中心对称的两个图形是全等形,对应角相等,对应线段平行(或在同一直线上)且相等;(2)中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分;中心对称的识别方法一:利用定义识别.方法二:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点中心对称.
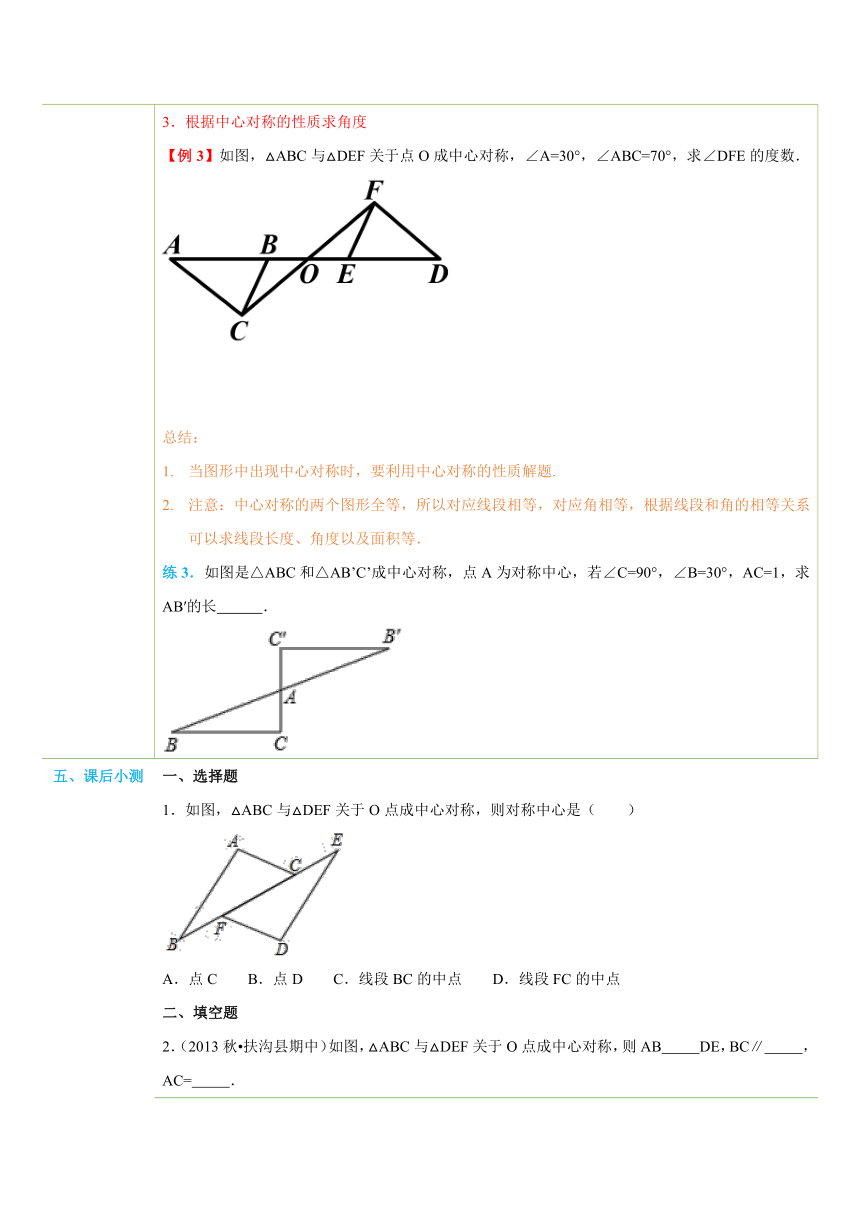
四、典例探究 扫一扫,有惊喜哦!1.已知一个图形和对称中心点O,画关于点O对称的图形【例1】画出△ABC关于点O中心对称的图形. ( http: / / www.21cnjy.com )总结:画一个点关于某点(对称中心)的对称点的画法是:先连接这个点与对称中心,再延长一倍即可.画一个图形关于某点的对称图形的画法是:先画 ( http: / / www.21cnjy.com )出图形中的几个特殊点(如多边形的顶点、线段的端点、圆的圆心等)关于某点的对称点,然后再顺次连结各对称点即可.练1.画出如图所示的两个半圆关于点B成中心对称的图形. ( http: / / www.21cnjy.com )2.已知中心对称的两个图形,画出对称中心【例2】如图所示,已知两个三角形成中心对称.请画出对称中心. ( http: / / www.21cnjy.com )总结:确定对称中心的两种方法:(1)找出一对对应点,连线的中点即为对称中心;(2)找出两对对应点,连线的交点即为对称中心.练2.如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由. ( http: / / www.21cnjy.com )3.根据中心对称的性质求角度【例3】如图,△ABC与△DEF关于点O成中心对称,∠A=30°,∠ABC=70°,求∠DFE的度数. ( http: / / www.21cnjy.com )总结:当图形中出现中心对称时,要利用中心对称的性质解题.注意:中心对称的两个图形全等,所以对应线段相等,对应角相等,根据线段和角的相等关系可以求线段长度、角度以及面积等.练3.如图是△ABC和△AB’C’成中心对称,点A为对称中心,若∠C=90°,∠B=30°,AC=1,求AB′的长 . ( http: / / www.21cnjy.com )
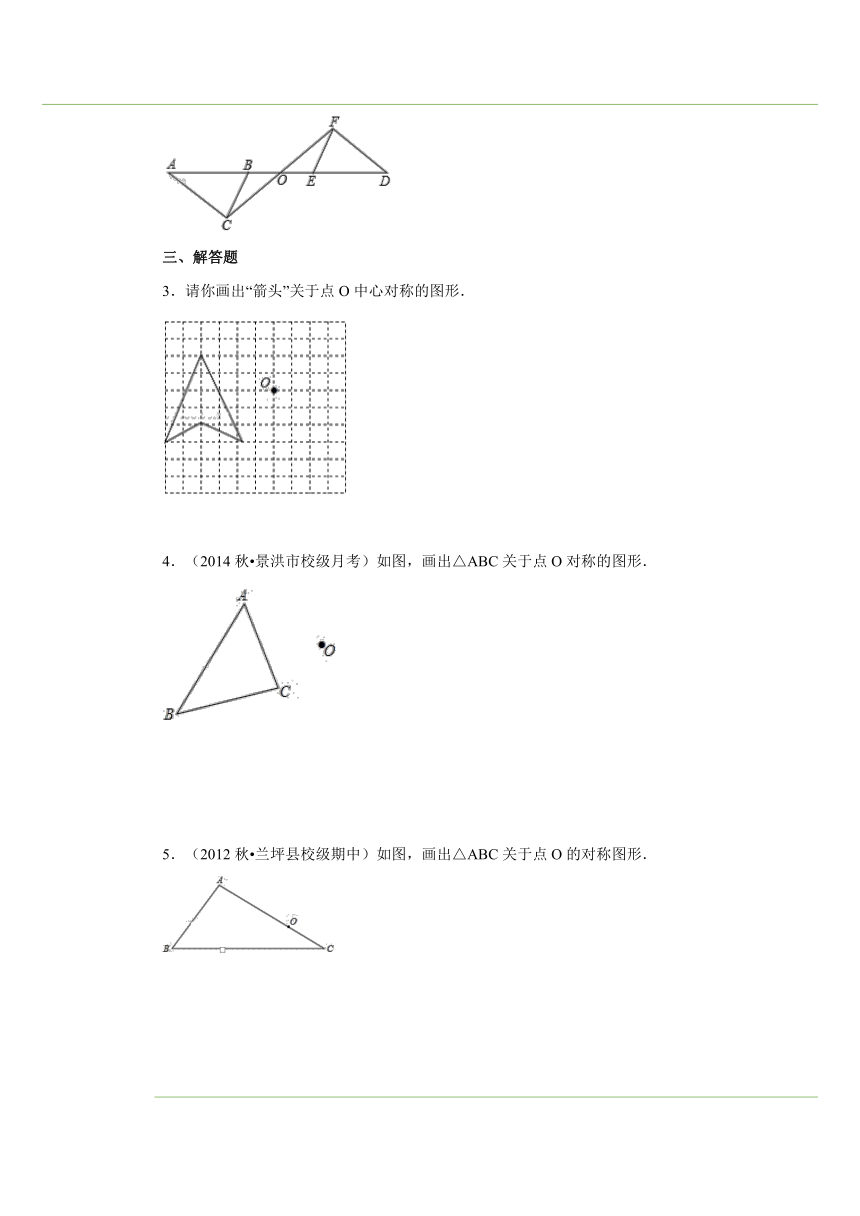
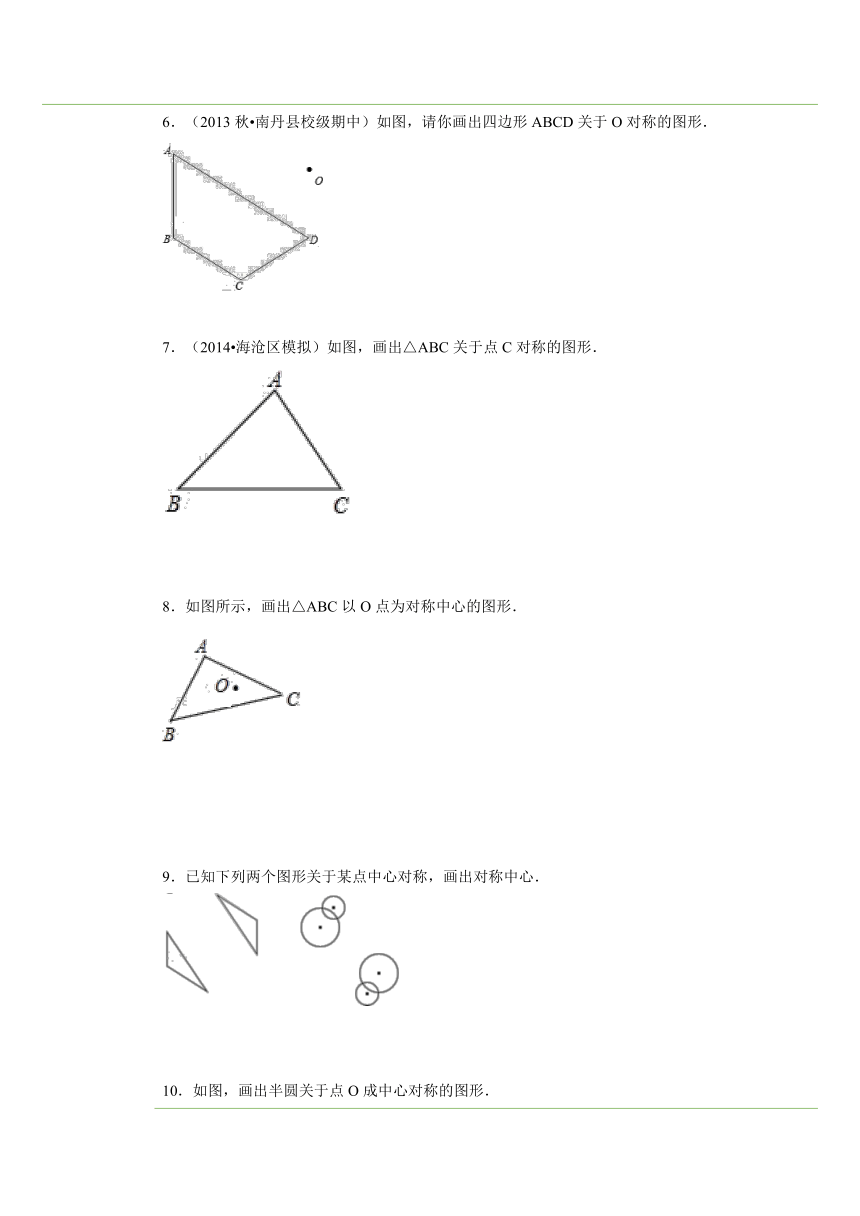
五、课后小测 一、选择题1.如图,△ABC与△DEF关于O点成中心对称,则对称中心是( ) ( http: / / www.21cnjy.com )A.点C B.点D C.线段BC的中点 D.线段FC的中点二、填空题2.(2013秋 扶沟县期中)如图,△ABC与△DEF关于O点成中心对称,则AB DE,BC∥ ,AC= . ( http: / / www.21cnjy.com )三、解答题3.请你画出“箭头”关于点O中心对称的图形. ( http: / / www.21cnjy.com )4.(2014秋 景洪市校级月考)如图,画出△ABC关于点O对称的图形. ( http: / / www.21cnjy.com )5.(2012秋 兰坪县校级期中)如图,画出△ABC关于点O的对称图形. ( http: / / www.21cnjy.com )6.(2013秋 南丹县校级期中)如图,请你画出四边形ABCD关于O对称的图形. ( http: / / www.21cnjy.com )7.(2014 海沧区模拟)如图,画出△ABC关于点C对称的图形. ( http: / / www.21cnjy.com )8.如图所示,画出△ABC以O点为对称中心的图形. ( http: / / www.21cnjy.com )9.已知下列两个图形关于某点中心对称,画出对称中心. ( http: / / www.21cnjy.com )10.如图,画出半圆关于点O成中心对称的图形. ( http: / / www.21cnjy.com )11.如图,两个半圆分别以P、Q为圆心,它 ( http: / / www.21cnjy.com )们的半径相等,A1、P、B1、B2、Q、A2在同一条直线上.这个图形中的两个半圆是否成中心对称?如果是,请找出对称中心O. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】分析:根据对称中心平分对应点连线,可得出各点的对应点,顺次连接即可得出△ABC关于点O中心对称的图形.
解答:解:所作图形如下:
( http: / / www.21cnjy.com )
点评:本题考查了旋转作图的知识,解答本题的关键是根据对称中心平分对应点连线得到各点的对称点,难度一般.
练1.分析:分别找到A、C、D三点关于点B的中心对称点,继而确定两半圆的直径,作半圆即可.
解答:解:如图所示:
( http: / / www.21cnjy.com ).
点评:本题考查了旋转作图的知识,解答本题的关键是根据中心对称的性质找到各点的对应点.
【例2】分析:对应点连线的交点即是对称中心.
解答:解:如图所示:点O即是两三角形的对称中心.
( http: / / www.21cnjy.com )
点评:本题考查了旋转作图的知识,若两个图形成中心对称关系,则对应点连线交于一点,这一点即是对称中心.
练2.分析:根据中心对称的性质,连接任意两对对应点,交点即为对称中心.
解答:解:如图所示,点O即为对称中心.
理由如下:∵四边形ABCD与四边形EFGH成中心对称,
∴BF过对称中心,CG过对称中心,
∴BF、CG的交点即为对称中心.
( http: / / www.21cnjy.com )
点评:本题考查了利用旋转变换作图,中心对称图形的性质,是基础题,比较简单,熟记性质是解题的关键.
【例3】分析:利用关于某点对称的图形全等,这样可以得出対应边与对应角之间的关系,进而解决.
解答:解:∵△ABC与△DEF关于O点成中心对称,
∴△ABC≌△DEF,
∴∠DEF=∠ABC=70°,∠D=∠A=30°,
∴∠DFE=180°-∠DEF-∠D=80°.
点评:此题主要考查中心对称的性质,难度不大,比较典型.
练3.分析:利用中心对称图形关于A为对称中心,得出两图形全等,即可解决.
解答:解:∵此图是中心对称图形,A为对称中心,
∴△BAC≌△B′AC′,
∴∠B=∠B′,∠C=∠C′,AC=AC′
∵∠C=90°,∠B=30°,AC=1,
∴AB′=2AC′=2.
故答案为:2.
点评:此题主要考查了中心对称图形的性质,以及在直角三角形中30°,所对的直角边是斜边的一半.
课后小测答案:
一、选择题
1.解:∵此图形是中心对称图形,
∴对称中心是线段FC的中点.
故选:D.
二、填空题
2.解:∵△ABC与△DEF关于O点成中心对称,
∴△ABC≌△DEF,AB=DE,AC=DF.
又∵BO=OE,CO=OF,∠BOC=∠FOE,
∴△BOC≌△EOF,
∴∠BCO=∠OFE,BC∥EF.
故填:=,EF,DF.
三、解答题
3.解:如图所示:即为所求.
( http: / / www.21cnjy.com )
4.解:如图所示:△A′B′C′即为所求.
( http: / / www.21cnjy.com )
5.解:如图,△A′B′C′即为所求图形.
( http: / / www.21cnjy.com )
6.解:根据题意画出图形,如图所示:
( http: / / www.21cnjy.com )
∴四边形A′B′C′D′为所求作的四边形.
7.解:△ABC关于点C对称的图形△A′B′C如图所示.
( http: / / www.21cnjy.com )
8.解:
( http: / / www.21cnjy.com )
9.解:如图所示:点O,W即为图形的对称中心.
( http: / / www.21cnjy.com )
10.解:作半圆的直径的两外端与点O的连线并延长相同长度,确定旋转后的直径,然后画半圆.
( http: / / www.21cnjy.com ).
11.解:是中心对称图形,对称中心如图.
( http: / / www.21cnjy.com )
二、知识回顾 1.什么是两个图形成轴对称?成轴对称的两个图形有哪些性质?把一个图形沿着某一条直线折叠能与另一个图形完全重合,那么就说这两个图形关于这条直线对称或成轴对称.性质:成轴对称的两个图形是全等形,对称轴是对称点连线的垂直平分线.2.什么是旋转?旋转的特征是什么?在平面内,将一个图形绕一个定点旋转一定角度,这样的图形变换称为图形的旋转.性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前后的图形全等,对应线段相等,对应角相等.
三、新知讲解 中心对称把一个图形绕着某一个点旋转180°,如果 ( http: / / www.21cnjy.com )它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这个两个图形中的对应点叫做关于对称中心的对称点.中心对称的性质(1)中心对称的两个图形是全等形,对应角相等,对应线段平行(或在同一直线上)且相等;(2)中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分;中心对称的识别方法一:利用定义识别.方法二:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点中心对称.
四、典例探究 扫一扫,有惊喜哦!1.已知一个图形和对称中心点O,画关于点O对称的图形【例1】画出△ABC关于点O中心对称的图形. ( http: / / www.21cnjy.com )总结:画一个点关于某点(对称中心)的对称点的画法是:先连接这个点与对称中心,再延长一倍即可.画一个图形关于某点的对称图形的画法是:先画 ( http: / / www.21cnjy.com )出图形中的几个特殊点(如多边形的顶点、线段的端点、圆的圆心等)关于某点的对称点,然后再顺次连结各对称点即可.练1.画出如图所示的两个半圆关于点B成中心对称的图形. ( http: / / www.21cnjy.com )2.已知中心对称的两个图形,画出对称中心【例2】如图所示,已知两个三角形成中心对称.请画出对称中心. ( http: / / www.21cnjy.com )总结:确定对称中心的两种方法:(1)找出一对对应点,连线的中点即为对称中心;(2)找出两对对应点,连线的交点即为对称中心.练2.如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由. ( http: / / www.21cnjy.com )3.根据中心对称的性质求角度【例3】如图,△ABC与△DEF关于点O成中心对称,∠A=30°,∠ABC=70°,求∠DFE的度数. ( http: / / www.21cnjy.com )总结:当图形中出现中心对称时,要利用中心对称的性质解题.注意:中心对称的两个图形全等,所以对应线段相等,对应角相等,根据线段和角的相等关系可以求线段长度、角度以及面积等.练3.如图是△ABC和△AB’C’成中心对称,点A为对称中心,若∠C=90°,∠B=30°,AC=1,求AB′的长 . ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.如图,△ABC与△DEF关于O点成中心对称,则对称中心是( ) ( http: / / www.21cnjy.com )A.点C B.点D C.线段BC的中点 D.线段FC的中点二、填空题2.(2013秋 扶沟县期中)如图,△ABC与△DEF关于O点成中心对称,则AB DE,BC∥ ,AC= . ( http: / / www.21cnjy.com )三、解答题3.请你画出“箭头”关于点O中心对称的图形. ( http: / / www.21cnjy.com )4.(2014秋 景洪市校级月考)如图,画出△ABC关于点O对称的图形. ( http: / / www.21cnjy.com )5.(2012秋 兰坪县校级期中)如图,画出△ABC关于点O的对称图形. ( http: / / www.21cnjy.com )6.(2013秋 南丹县校级期中)如图,请你画出四边形ABCD关于O对称的图形. ( http: / / www.21cnjy.com )7.(2014 海沧区模拟)如图,画出△ABC关于点C对称的图形. ( http: / / www.21cnjy.com )8.如图所示,画出△ABC以O点为对称中心的图形. ( http: / / www.21cnjy.com )9.已知下列两个图形关于某点中心对称,画出对称中心. ( http: / / www.21cnjy.com )10.如图,画出半圆关于点O成中心对称的图形. ( http: / / www.21cnjy.com )11.如图,两个半圆分别以P、Q为圆心,它 ( http: / / www.21cnjy.com )们的半径相等,A1、P、B1、B2、Q、A2在同一条直线上.这个图形中的两个半圆是否成中心对称?如果是,请找出对称中心O. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】分析:根据对称中心平分对应点连线,可得出各点的对应点,顺次连接即可得出△ABC关于点O中心对称的图形.
解答:解:所作图形如下:
( http: / / www.21cnjy.com )
点评:本题考查了旋转作图的知识,解答本题的关键是根据对称中心平分对应点连线得到各点的对称点,难度一般.
练1.分析:分别找到A、C、D三点关于点B的中心对称点,继而确定两半圆的直径,作半圆即可.
解答:解:如图所示:
( http: / / www.21cnjy.com ).
点评:本题考查了旋转作图的知识,解答本题的关键是根据中心对称的性质找到各点的对应点.
【例2】分析:对应点连线的交点即是对称中心.
解答:解:如图所示:点O即是两三角形的对称中心.
( http: / / www.21cnjy.com )
点评:本题考查了旋转作图的知识,若两个图形成中心对称关系,则对应点连线交于一点,这一点即是对称中心.
练2.分析:根据中心对称的性质,连接任意两对对应点,交点即为对称中心.
解答:解:如图所示,点O即为对称中心.
理由如下:∵四边形ABCD与四边形EFGH成中心对称,
∴BF过对称中心,CG过对称中心,
∴BF、CG的交点即为对称中心.
( http: / / www.21cnjy.com )
点评:本题考查了利用旋转变换作图,中心对称图形的性质,是基础题,比较简单,熟记性质是解题的关键.
【例3】分析:利用关于某点对称的图形全等,这样可以得出対应边与对应角之间的关系,进而解决.
解答:解:∵△ABC与△DEF关于O点成中心对称,
∴△ABC≌△DEF,
∴∠DEF=∠ABC=70°,∠D=∠A=30°,
∴∠DFE=180°-∠DEF-∠D=80°.
点评:此题主要考查中心对称的性质,难度不大,比较典型.
练3.分析:利用中心对称图形关于A为对称中心,得出两图形全等,即可解决.
解答:解:∵此图是中心对称图形,A为对称中心,
∴△BAC≌△B′AC′,
∴∠B=∠B′,∠C=∠C′,AC=AC′
∵∠C=90°,∠B=30°,AC=1,
∴AB′=2AC′=2.
故答案为:2.
点评:此题主要考查了中心对称图形的性质,以及在直角三角形中30°,所对的直角边是斜边的一半.
课后小测答案:
一、选择题
1.解:∵此图形是中心对称图形,
∴对称中心是线段FC的中点.
故选:D.
二、填空题
2.解:∵△ABC与△DEF关于O点成中心对称,
∴△ABC≌△DEF,AB=DE,AC=DF.
又∵BO=OE,CO=OF,∠BOC=∠FOE,
∴△BOC≌△EOF,
∴∠BCO=∠OFE,BC∥EF.
故填:=,EF,DF.
三、解答题
3.解:如图所示:即为所求.
( http: / / www.21cnjy.com )
4.解:如图所示:△A′B′C′即为所求.
( http: / / www.21cnjy.com )
5.解:如图,△A′B′C′即为所求图形.
( http: / / www.21cnjy.com )
6.解:根据题意画出图形,如图所示:
( http: / / www.21cnjy.com )
∴四边形A′B′C′D′为所求作的四边形.
7.解:△ABC关于点C对称的图形△A′B′C如图所示.
( http: / / www.21cnjy.com )
8.解:
( http: / / www.21cnjy.com )
9.解:如图所示:点O,W即为图形的对称中心.
( http: / / www.21cnjy.com )
10.解:作半圆的直径的两外端与点O的连线并延长相同长度,确定旋转后的直径,然后画半圆.
( http: / / www.21cnjy.com ).
11.解:是中心对称图形,对称中心如图.
( http: / / www.21cnjy.com )
同课章节目录
