19.1多边形内角和(2) 课件(共21张PPT)
文档属性
| 名称 | 19.1多边形内角和(2) 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 643.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
19.1多边形内角和(2)
教学目标:
1.理解多边形的外角的概念;
2.掌握多边形外角和的结论;
教学重点:探索多边形的外角和的结论
教学难点:
如何把多边形转化成三角形,用分割
多边形法推导多边形的外角和.
A
B
C
D
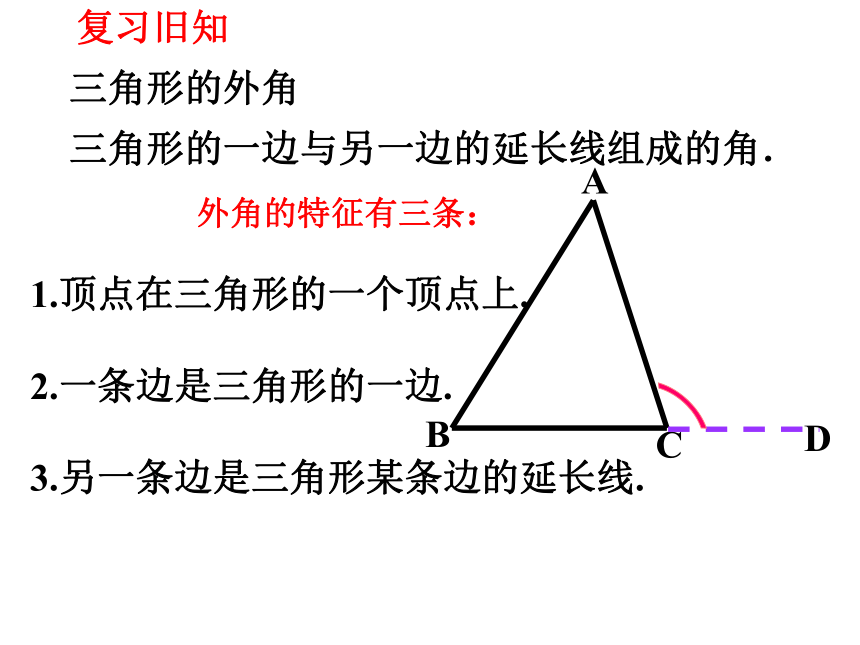
三角形的外角
三角形的一边与另一边的延长线组成的角.
外角的特征有三条:
1.顶点在三角形的一个顶点上.
2.一条边是三角形的一边.
3.另一条边是三角形某条边的延长线.
复习旧知
A
B
C
1
2
3
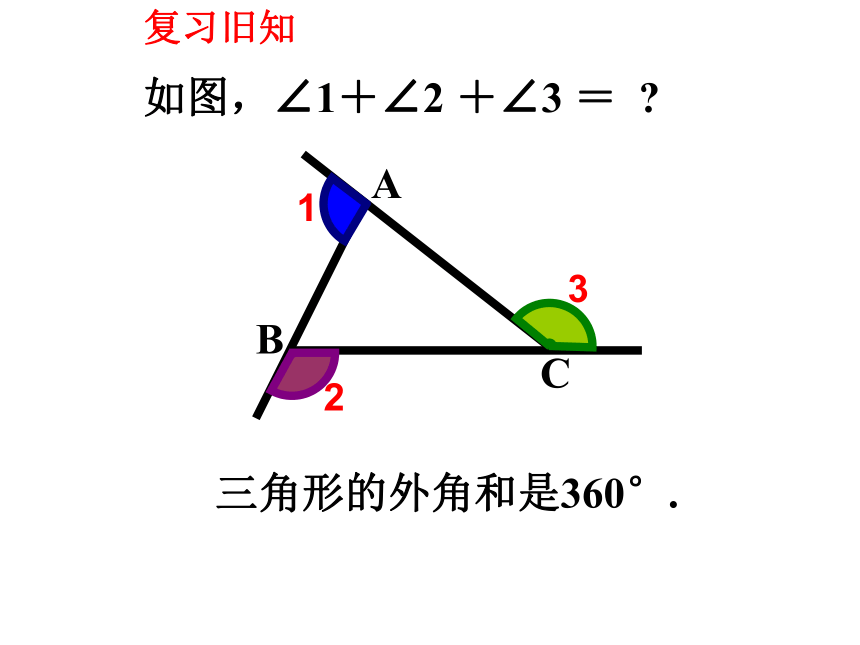
如图,∠1+∠2 +∠3 =
三角形的外角和是360°.
复习旧知
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.
4
2
6
5
1
3
D
E
B
F
C
A
六边形的外角和等于多少
探究新知
∠1+∠2+∠3+∠4+∠5+∠6=
∵六边形的外角与相邻内角互补,
4
2
6
5
1
3
D
E
B
F
C
A
n边形的外角和会是多少?
=6个平角
- 6边形内角和
=6×180°
-(6-2)×180°
=360 °
结论:六边形的外角和等于360°.
∴六边形的外角和
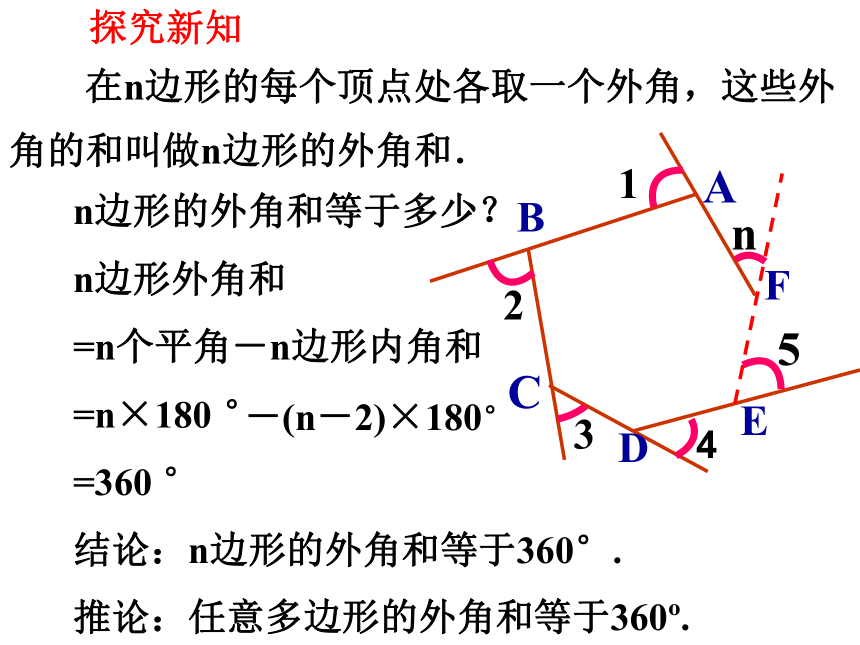
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2)×180°
=360 °
A
1
E
B
C
D
2
3
5
F
n
=n个平角-n边形内角和
=n×180 °
4
n边形的外角和等于多少?
任意多边形的外角和等于360 .
推论:
探究新知
例题:一个多边形的每一个内角都是150°,你知道它是几边形吗?
解:设这个多边形为n边形,根据题意得:
(n-2) 180°=
解得 n=12
答:这个多边形是十二边形.
150° n
例题解析
解:∵多边形外角和等于360°,
∴这个正多边形的每个外角为
∴这个正多边形的边数为
360°÷30°=12.
180°-150°=30°,
例题:一个多边形的每一个内角都是150°,你知道它是几边形吗?
1.一个多边形每个外角都是60°,这个多边形是 边形,内角和是 度, 外角和是 度;
2.多边形边数每增加一条,它的内角和会增加 ,外角和增加 .
六
720
360
180°
0°
练习巩固
认一认:
多边形中,如果各条边都相等,各个内角都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
例 已知一个多边形,它的内角和等于
外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n,
∵它的内角和等于 (n-2) 180°,
它的外角和等于360 ,
∴ (n-2) 180°= .
解得: n=6
∴这个多边形的边数为6.
× 2
360
例题解析
例 求正六边形每个内角的度数.
解:∵正六边形内角和为,
(6-2) 180°= .
∴每个内角的度数为.
=120°.
720
720°÷6
例题解析
(2)已知一个多边形的内角和为900° ,则这个多边形是_____边形.
七
(1)十边形的内角和为_____,外角和为_____.
1440°
360°
练习巩固
(3)已知一个多边形的每一个外角都是72°,则这个多边形的边数为____.
5
(4)在五边形ABCDE中,若∠A=∠D=90°,且∠B:∠C:∠E=3:2:4,则∠C的度数为_____.
80°
练习巩固
四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
(1)本节课我们学习了哪些知识?
(2)多边形的外角和的结论是什么?
(3)如何将多边形分割成三角形?
课堂小结
1.四边形ABCD中,四个内角度数之比是
1:2:3:4,求出四个内角的度数.
解:∵四边形内角和为360°,
∴每个内角的度数为:
360°×
1
10
=36°,
360°×
2
10
=72°,
360°×
3
10
=108°,
360°×
4
10
=144°.
巩固提高
2.一个多边形的内角和是1440°,求
这个多边形的边数.
解: 设多边形的边数为n,
∵它的内角和等于 (n-2) 180°,
∴ (n-2) 180°= .
解得: n=10
∴这个多边形的边数为10.
1440
3.正多边形每个内角度数可能是:
(1)75°;(2)90°;(3)120°?说明理由.
解:(1)不可能 .
∵与75°相邻的外角度数为105°,
而105°的整数倍不可能等于360°.
(2)、(3)可能 .
今天作业
课本P74页第2、3、4 题
19.1多边形内角和(2)
教学目标:
1.理解多边形的外角的概念;
2.掌握多边形外角和的结论;
教学重点:探索多边形的外角和的结论
教学难点:
如何把多边形转化成三角形,用分割
多边形法推导多边形的外角和.
A
B
C
D
三角形的外角
三角形的一边与另一边的延长线组成的角.
外角的特征有三条:
1.顶点在三角形的一个顶点上.
2.一条边是三角形的一边.
3.另一条边是三角形某条边的延长线.
复习旧知
A
B
C
1
2
3
如图,∠1+∠2 +∠3 =
三角形的外角和是360°.
复习旧知
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.
4
2
6
5
1
3
D
E
B
F
C
A
六边形的外角和等于多少
探究新知
∠1+∠2+∠3+∠4+∠5+∠6=
∵六边形的外角与相邻内角互补,
4
2
6
5
1
3
D
E
B
F
C
A
n边形的外角和会是多少?
=6个平角
- 6边形内角和
=6×180°
-(6-2)×180°
=360 °
结论:六边形的外角和等于360°.
∴六边形的外角和
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2)×180°
=360 °
A
1
E
B
C
D
2
3
5
F
n
=n个平角-n边形内角和
=n×180 °
4
n边形的外角和等于多少?
任意多边形的外角和等于360 .
推论:
探究新知
例题:一个多边形的每一个内角都是150°,你知道它是几边形吗?
解:设这个多边形为n边形,根据题意得:
(n-2) 180°=
解得 n=12
答:这个多边形是十二边形.
150° n
例题解析
解:∵多边形外角和等于360°,
∴这个正多边形的每个外角为
∴这个正多边形的边数为
360°÷30°=12.
180°-150°=30°,
例题:一个多边形的每一个内角都是150°,你知道它是几边形吗?
1.一个多边形每个外角都是60°,这个多边形是 边形,内角和是 度, 外角和是 度;
2.多边形边数每增加一条,它的内角和会增加 ,外角和增加 .
六
720
360
180°
0°
练习巩固
认一认:
多边形中,如果各条边都相等,各个内角都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
例 已知一个多边形,它的内角和等于
外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n,
∵它的内角和等于 (n-2) 180°,
它的外角和等于360 ,
∴ (n-2) 180°= .
解得: n=6
∴这个多边形的边数为6.
× 2
360
例题解析
例 求正六边形每个内角的度数.
解:∵正六边形内角和为,
(6-2) 180°= .
∴每个内角的度数为.
=120°.
720
720°÷6
例题解析
(2)已知一个多边形的内角和为900° ,则这个多边形是_____边形.
七
(1)十边形的内角和为_____,外角和为_____.
1440°
360°
练习巩固
(3)已知一个多边形的每一个外角都是72°,则这个多边形的边数为____.
5
(4)在五边形ABCDE中,若∠A=∠D=90°,且∠B:∠C:∠E=3:2:4,则∠C的度数为_____.
80°
练习巩固
四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
(1)本节课我们学习了哪些知识?
(2)多边形的外角和的结论是什么?
(3)如何将多边形分割成三角形?
课堂小结
1.四边形ABCD中,四个内角度数之比是
1:2:3:4,求出四个内角的度数.
解:∵四边形内角和为360°,
∴每个内角的度数为:
360°×
1
10
=36°,
360°×
2
10
=72°,
360°×
3
10
=108°,
360°×
4
10
=144°.
巩固提高
2.一个多边形的内角和是1440°,求
这个多边形的边数.
解: 设多边形的边数为n,
∵它的内角和等于 (n-2) 180°,
∴ (n-2) 180°= .
解得: n=10
∴这个多边形的边数为10.
1440
3.正多边形每个内角度数可能是:
(1)75°;(2)90°;(3)120°?说明理由.
解:(1)不可能 .
∵与75°相邻的外角度数为105°,
而105°的整数倍不可能等于360°.
(2)、(3)可能 .
今天作业
课本P74页第2、3、4 题
