初中数学人教版七年级下册 5.4 平移-教学设计(表格式)
文档属性
| 名称 | 初中数学人教版七年级下册 5.4 平移-教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 1023.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 10:11:30 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 七年级 学期 春季
课题 5.4平移
教学目标
了解平移的特征,能发现特殊图案的共同点,并能根据这个特点绘制图形。 能发现、归纳图形平移的特征,体会从数学的角度理解问题。 3.感受数学活动充满了探索性与创造性,促进学生乐于探究。
教学内容
教学重点: 理解平移的概念及性质;
2. 对平移的认识和性质的探索. 教学难点: 1. 理解平移的性质2的探索;
2.对平移性质的运用.
教学过程
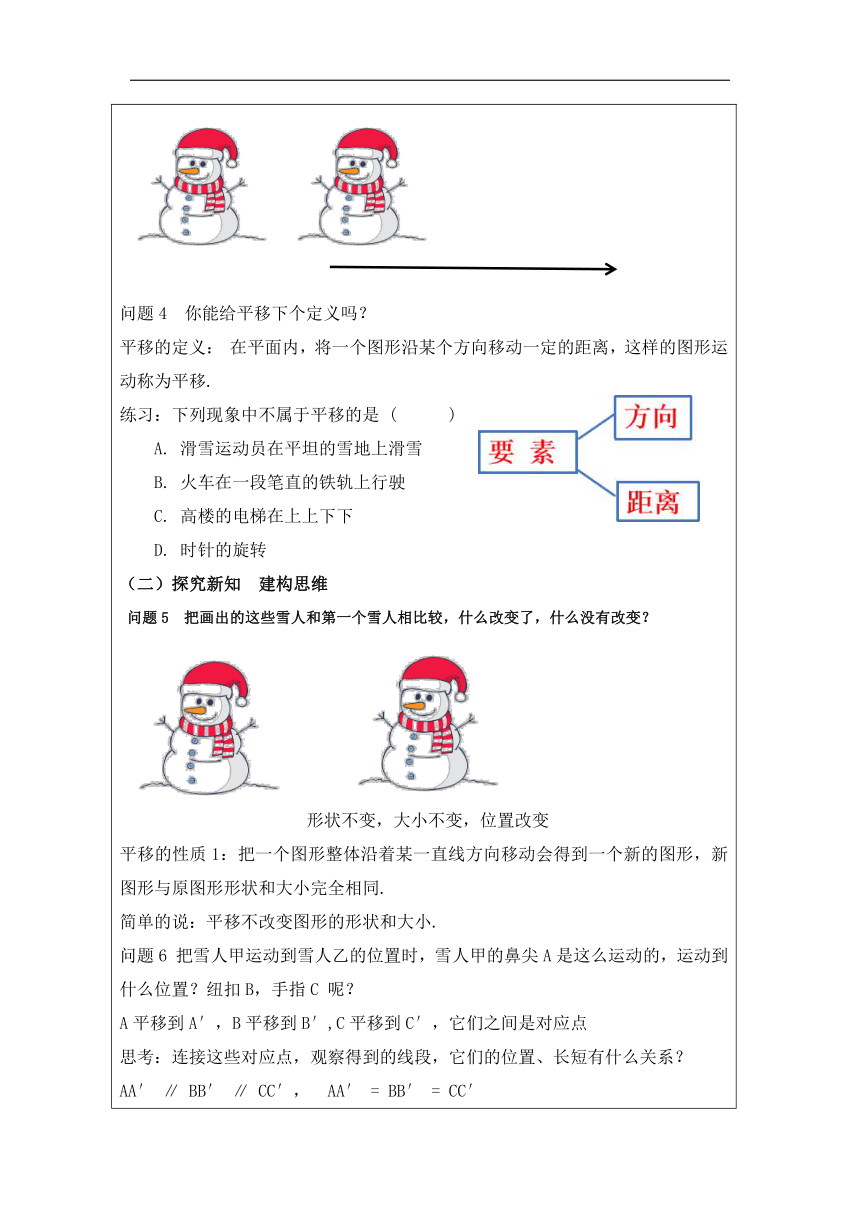
(一)问题驱动 激活思维 问题1:仔细观察这些美丽的图案,它们有什么共同的特点? 问题2 这些图案能否根据其中一部分绘制整个图案? 问题3 如何在一张半透明的纸上,画出一排形状和大小如图所示雪人呢? 问题4 你能给平移下个定义吗? 平移的定义: 在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移. 练习:下列现象中不属于平移的是 ( ) A. 滑雪运动员在平坦的雪地上滑雪 B. 火车在一段笔直的铁轨上行驶 C. 高楼的电梯在上上下下 D. 时针的旋转 探究新知 建构思维 问题5 把画出的这些雪人和第一个雪人相比较,什么改变了,什么没有改变? 形状不变,大小不变,位置改变 平移的性质1:把一个图形整体沿着某一直线方向移动会得到一个新的图形,新图形与原图形形状和大小完全相同. 简单的说:平移不改变图形的形状和大小. 问题6 把雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是这么运动的,运动到什么位置?纽扣B,手指C 呢? A平移到A′,B平移到B′,C平移到C′,它们之间是对应点 思考:连接这些对应点,观察得到的线段,它们的位置、长短有什么关系? AA′ ∥ BB′ ∥ CC′, AA′ = BB′ = CC′ 平移的性质2 :连接各组对应点的线段平行(或都在同一条直线上)且相等. 思考:平移的方向不同,结论是否仍然成立? 简单的说:对应点连线平行(或在同一条直线上)且相等. 应用迁移 拓展思维 例1 将线段AB平移,使点A与点D 对应. 1.连结AD 2.过点B作AD的平行线m 3.在平行线m上截取线段BC,使BC=AD 4.连结CD 变式 如图,平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′. 思考1 画出三角形A′B′C′,关键是确定什么? 确定三个顶点:A'、B'、C' 思考2 图形平移后对应点有什么特征? 连接各组对应点的线段平行且相等 总结归纳:如图进行平移作图 (1)确定图形的关键点(例如:三角形的三个顶点); (2)利用平移的性质作出关键点对应点; (3)顺次连结对应点. 练习1 如下图,图中哪条线段可以由线段 b 经过平移得到?如何进行平移? 练习2 如图,将三角形 ABC 沿着 BC 方向平移至三角形 DEF 处.若 EC = 2BE = 4,则 CF 的长为 . 思路点拨 根据平移的性质解题. 拓展 如图是一块长方形的草地,长为 21 m,宽为 15 m. 在草地上有一条宽为 1 m 的小道,长方形的草地上除小道外长满青草. 问长草部分的面积为多少 思路点拨 平移构成规则图形. 解:长草部分的面积为 (21 - 1)×15 = 300 (m ) 梳理小结 深化思维
课程基本信息
学科 数学 年级 七年级 学期 春季
课题 5.4平移
教学目标
了解平移的特征,能发现特殊图案的共同点,并能根据这个特点绘制图形。 能发现、归纳图形平移的特征,体会从数学的角度理解问题。 3.感受数学活动充满了探索性与创造性,促进学生乐于探究。
教学内容
教学重点: 理解平移的概念及性质;
2. 对平移的认识和性质的探索. 教学难点: 1. 理解平移的性质2的探索;
2.对平移性质的运用.
教学过程
(一)问题驱动 激活思维 问题1:仔细观察这些美丽的图案,它们有什么共同的特点? 问题2 这些图案能否根据其中一部分绘制整个图案? 问题3 如何在一张半透明的纸上,画出一排形状和大小如图所示雪人呢? 问题4 你能给平移下个定义吗? 平移的定义: 在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移. 练习:下列现象中不属于平移的是 ( ) A. 滑雪运动员在平坦的雪地上滑雪 B. 火车在一段笔直的铁轨上行驶 C. 高楼的电梯在上上下下 D. 时针的旋转 探究新知 建构思维 问题5 把画出的这些雪人和第一个雪人相比较,什么改变了,什么没有改变? 形状不变,大小不变,位置改变 平移的性质1:把一个图形整体沿着某一直线方向移动会得到一个新的图形,新图形与原图形形状和大小完全相同. 简单的说:平移不改变图形的形状和大小. 问题6 把雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是这么运动的,运动到什么位置?纽扣B,手指C 呢? A平移到A′,B平移到B′,C平移到C′,它们之间是对应点 思考:连接这些对应点,观察得到的线段,它们的位置、长短有什么关系? AA′ ∥ BB′ ∥ CC′, AA′ = BB′ = CC′ 平移的性质2 :连接各组对应点的线段平行(或都在同一条直线上)且相等. 思考:平移的方向不同,结论是否仍然成立? 简单的说:对应点连线平行(或在同一条直线上)且相等. 应用迁移 拓展思维 例1 将线段AB平移,使点A与点D 对应. 1.连结AD 2.过点B作AD的平行线m 3.在平行线m上截取线段BC,使BC=AD 4.连结CD 变式 如图,平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′. 思考1 画出三角形A′B′C′,关键是确定什么? 确定三个顶点:A'、B'、C' 思考2 图形平移后对应点有什么特征? 连接各组对应点的线段平行且相等 总结归纳:如图进行平移作图 (1)确定图形的关键点(例如:三角形的三个顶点); (2)利用平移的性质作出关键点对应点; (3)顺次连结对应点. 练习1 如下图,图中哪条线段可以由线段 b 经过平移得到?如何进行平移? 练习2 如图,将三角形 ABC 沿着 BC 方向平移至三角形 DEF 处.若 EC = 2BE = 4,则 CF 的长为 . 思路点拨 根据平移的性质解题. 拓展 如图是一块长方形的草地,长为 21 m,宽为 15 m. 在草地上有一条宽为 1 m 的小道,长方形的草地上除小道外长满青草. 问长草部分的面积为多少 思路点拨 平移构成规则图形. 解:长草部分的面积为 (21 - 1)×15 = 300 (m ) 梳理小结 深化思维
