人教版数学七年级下册6.1 平方根(第二课时) 教案
文档属性
| 名称 | 人教版数学七年级下册6.1 平方根(第二课时) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 538.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 初中数学 年级 七年级 学期 春季
课题 6.1平方根(第二课时)
教学目标
1.了解夹逼法求一个数的算术平方根的近似值. 2.会用计算器求一个数的算术平方根;理解被开方数扩大(或缩小)与它的算术平方根扩大(或缩小)的规律.
教学内容
教学重点: 1.了解无限不循环小数在生活中是存在的,体验用夹逼法求一个数的算术平方根的近似值。
2.用计算器求一个数的算术平方根。
教学难点: 1.夹逼法及估计一个(无理)数的大小的思想。
教学过程
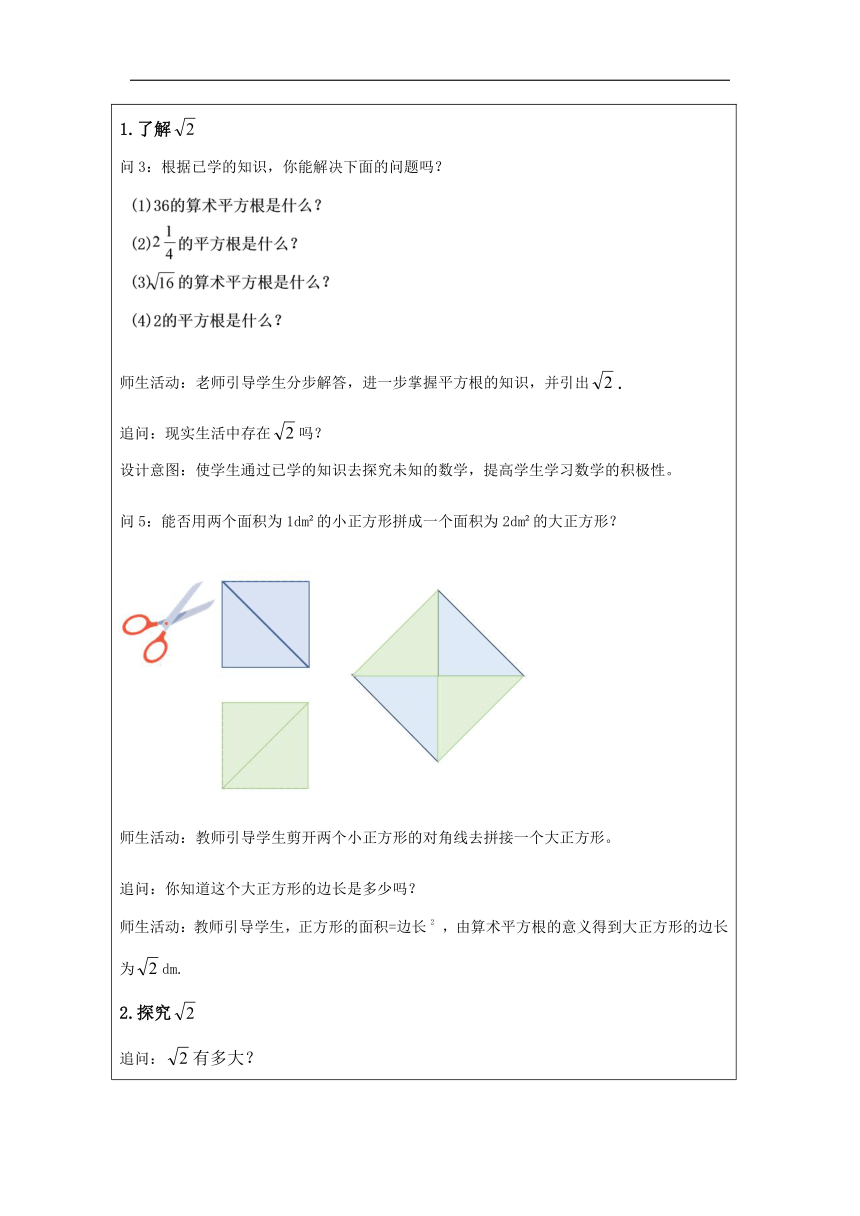
一、复习回顾,激活思维 问:什么是平方根? 师生活动:如果一个数的平方等于a,那么这个数叫做a的平方根。教师引导学生用数学语言表述:,. 问2:平方根怎么表示? 师生活动:教师引导 设计意图:复习回顾平方根和算术平方根的概念及表示方法,为接下来的学习内容做铺垫. 二、探究新知,构建思维 1.了解 问3:根据已学的知识,你能解决下面的问题吗? 师生活动:老师引导学生分步解答,进一步掌握平方根的知识,并引出. 追问:现实生活中存在吗? 设计意图:使学生通过已学的知识去探究未知的数学,提高学生学习数学的积极性。 问5:能否用两个面积为1dm 的小正方形拼成一个面积为2dm 的大正方形? 师生活动:教师引导学生剪开两个小正方形的对角线去拼接一个大正方形。 追问:你知道这个大正方形的边长是多少吗? 师生活动:教师引导学生,正方形的面积=边长2 ,由算术平方根的意义得到大正方形的边长为dm. 2.探究 追问:有多大? 师生活动:教师引导学生体验夹逼法估算的近似值,了解无限不循环小数的概念,观看数学史短片《带来的第一次数学危机》,并指出许多正有理数的算术平方根如、等都是无限不循环小数. 设计意图:通过体验夹逼法估算和观看数学史短片,让学生体会数学来源于生活,进一步提高学生学习数学的兴趣. 3.使用计算器 问8:如何计算这类无限不循环小数? 师生活动:教师引导学生利用计算器计算,并得出被开方数越大,对应的算术平方根也越大. 设计意图:会使用计算器求平方根是本章的一个教学要求,为接下来的探究问题做好准备. 师生活动:学生利用计算器计算填表.对照表格,教师引导学生得出规律:被开方数的小数点向右或向左移动2位,它的算术平方根的小数点就相应地向右或向左移动1位,并引导学生利用规律解决问题. 三、应用迁移,拓展思维 在生活中,我们经常遇到估计一个数的大小的问题. 小丽想用一块面积为400cm 为的正方形纸片,沿着边的方向剪出一块面积为300cm 的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗? 思考:裁出符合要求的纸片应满足什么条件? 师生活动:教师引导学生得出满足的条件为正方形纸片的边长>长方形纸片的长.然后学生计算、规范解答。 设计意图:使学生感受到估算能力是生活中需要的一种能力. 四、梳理小结,升华思维 设计意图:教师引导学生归纳本节课的知识要点,使学生对这样的非完全平方数的算术平方根有一个较为整体、全面的认识.
课程基本信息
学科 初中数学 年级 七年级 学期 春季
课题 6.1平方根(第二课时)
教学目标
1.了解夹逼法求一个数的算术平方根的近似值. 2.会用计算器求一个数的算术平方根;理解被开方数扩大(或缩小)与它的算术平方根扩大(或缩小)的规律.
教学内容
教学重点: 1.了解无限不循环小数在生活中是存在的,体验用夹逼法求一个数的算术平方根的近似值。
2.用计算器求一个数的算术平方根。
教学难点: 1.夹逼法及估计一个(无理)数的大小的思想。
教学过程
一、复习回顾,激活思维 问:什么是平方根? 师生活动:如果一个数的平方等于a,那么这个数叫做a的平方根。教师引导学生用数学语言表述:,. 问2:平方根怎么表示? 师生活动:教师引导 设计意图:复习回顾平方根和算术平方根的概念及表示方法,为接下来的学习内容做铺垫. 二、探究新知,构建思维 1.了解 问3:根据已学的知识,你能解决下面的问题吗? 师生活动:老师引导学生分步解答,进一步掌握平方根的知识,并引出. 追问:现实生活中存在吗? 设计意图:使学生通过已学的知识去探究未知的数学,提高学生学习数学的积极性。 问5:能否用两个面积为1dm 的小正方形拼成一个面积为2dm 的大正方形? 师生活动:教师引导学生剪开两个小正方形的对角线去拼接一个大正方形。 追问:你知道这个大正方形的边长是多少吗? 师生活动:教师引导学生,正方形的面积=边长2 ,由算术平方根的意义得到大正方形的边长为dm. 2.探究 追问:有多大? 师生活动:教师引导学生体验夹逼法估算的近似值,了解无限不循环小数的概念,观看数学史短片《带来的第一次数学危机》,并指出许多正有理数的算术平方根如、等都是无限不循环小数. 设计意图:通过体验夹逼法估算和观看数学史短片,让学生体会数学来源于生活,进一步提高学生学习数学的兴趣. 3.使用计算器 问8:如何计算这类无限不循环小数? 师生活动:教师引导学生利用计算器计算,并得出被开方数越大,对应的算术平方根也越大. 设计意图:会使用计算器求平方根是本章的一个教学要求,为接下来的探究问题做好准备. 师生活动:学生利用计算器计算填表.对照表格,教师引导学生得出规律:被开方数的小数点向右或向左移动2位,它的算术平方根的小数点就相应地向右或向左移动1位,并引导学生利用规律解决问题. 三、应用迁移,拓展思维 在生活中,我们经常遇到估计一个数的大小的问题. 小丽想用一块面积为400cm 为的正方形纸片,沿着边的方向剪出一块面积为300cm 的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗? 思考:裁出符合要求的纸片应满足什么条件? 师生活动:教师引导学生得出满足的条件为正方形纸片的边长>长方形纸片的长.然后学生计算、规范解答。 设计意图:使学生感受到估算能力是生活中需要的一种能力. 四、梳理小结,升华思维 设计意图:教师引导学生归纳本节课的知识要点,使学生对这样的非完全平方数的算术平方根有一个较为整体、全面的认识.
