人教版数学七年级下册6.3 实数 教案(表格式)
文档属性
| 名称 | 人教版数学七年级下册6.3 实数 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 288.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 11:01:06 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 七年级 学期 春季
课题 6.3实数
教学目标
1. 理解无理数的概念,会判断一个数是否为无理数;会把实数进行分类;理解实数与数轴的关系,并进行相关运用;了解实数范围内的相反数、绝对值的意义;能对实数进行简单的加减运算. 2. 类比有理数,确定无理数及实数的研究思路,领会“数”的学习通法. 3. 在类比有理数的学习过程中,体会分类、数形结合、对应等数学思想,并发展抽象能力、推理能力、运算能力等核心素养.
教学内容
教学重点: 1.正确认识无理数、实数的概念,会对实数按照一定的标准进行分类; 2.了解实数范围内的相反数、绝对值的意义. 3.能对实数进行简单的运算. 教学难点: 1. 理解对无理数概念的探究过程.
2.对实数概念、运算等的运用.
教学过程
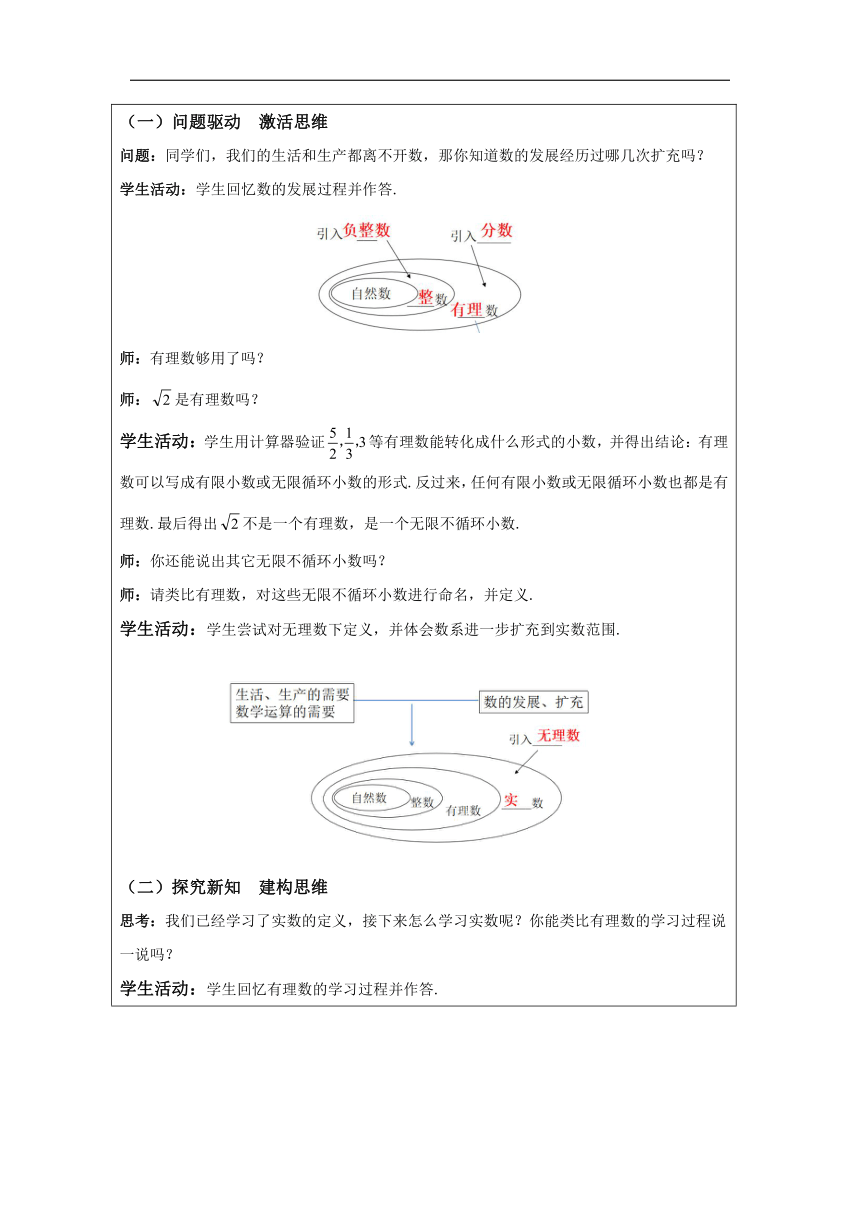
(一)问题驱动 激活思维 问题:同学们,我们的生活和生产都离不开数,那你知道数的发展经历过哪几次扩充吗? 学生活动:学生回忆数的发展过程并作答. 师:有理数够用了吗? 师:是有理数吗? 学生活动:学生用计算器验证等有理数能转化成什么形式的小数,并得出结论:有理数可以写成有限小数或无限循环小数的形式.反过来,任何有限小数或无限循环小数也都是有理数.最后得出不是一个有理数,是一个无限不循环小数. 师:你还能说出其它无限不循环小数吗? 师:请类比有理数,对这些无限不循环小数进行命名,并定义. 学生活动:学生尝试对无理数下定义,并体会数系进一步扩充到实数范围. 探究新知 建构思维 思考:我们已经学习了实数的定义,接下来怎么学习实数呢?你能类比有理数的学习过程说一说吗? 学生活动:学生回忆有理数的学习过程并作答.
师:类比有理数的分类,请同学们尝试对实数进行分类. 学生活动:学生按照不同的分类标准对实数进行分类,体会用类比有理数的方法对实数展开学习. 师:每个有理数都可以用数轴上的点来表示,那无理数能否用数轴上的点来表示呢?你能在数轴上找到表示π的点吗? 师:请同学们自主探究用数轴上的点表示. 师:结合数轴我们可以研究实数之间的关系,比如大小关系,你能快速比较出刚才表示的这几个数的大小吗? 师:除了大小关系外,你从数轴上还发现了什么关系? 学生活动:学生体会实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.有理数的大小比较法则、相反数、绝对值的意义在实数范围内同样适用. 应用迁移 拓展思维 例题演练 例:(1)分别写出的相反数; (2)指出分别是什么数的相反数; (3)求的绝对值; (4)已知一个数的绝对值,求这个数. 学生活动:学生思考求相反数、绝对值的方法,规范书写,并进一步体会到相反数、绝对值的意义同样合适于实数. 例: 计算下列各式的值: (1); (2). 学生活动:学生体会在进行实数的加减运算时,有理数的运算法则、运算性质等同样适用. 生长拓学: 如图,一根细线上端固定,下端系一个小重物,让这个小重物来回自由摆动,来回摆动一次所用的时间t(单位:s)与细线的长度l(单位:m)之间满足关系.当细线的长度为0.2 m时,小重物来回摆动一次所用的时间是多少(结果保留小数点后一位)? 学生活动:学生体会用实数的运算解决实际问题,进一步增强应用数学的意识. 梳理小结 深化思维
课程基本信息
学科 数学 年级 七年级 学期 春季
课题 6.3实数
教学目标
1. 理解无理数的概念,会判断一个数是否为无理数;会把实数进行分类;理解实数与数轴的关系,并进行相关运用;了解实数范围内的相反数、绝对值的意义;能对实数进行简单的加减运算. 2. 类比有理数,确定无理数及实数的研究思路,领会“数”的学习通法. 3. 在类比有理数的学习过程中,体会分类、数形结合、对应等数学思想,并发展抽象能力、推理能力、运算能力等核心素养.
教学内容
教学重点: 1.正确认识无理数、实数的概念,会对实数按照一定的标准进行分类; 2.了解实数范围内的相反数、绝对值的意义. 3.能对实数进行简单的运算. 教学难点: 1. 理解对无理数概念的探究过程.
2.对实数概念、运算等的运用.
教学过程
(一)问题驱动 激活思维 问题:同学们,我们的生活和生产都离不开数,那你知道数的发展经历过哪几次扩充吗? 学生活动:学生回忆数的发展过程并作答. 师:有理数够用了吗? 师:是有理数吗? 学生活动:学生用计算器验证等有理数能转化成什么形式的小数,并得出结论:有理数可以写成有限小数或无限循环小数的形式.反过来,任何有限小数或无限循环小数也都是有理数.最后得出不是一个有理数,是一个无限不循环小数. 师:你还能说出其它无限不循环小数吗? 师:请类比有理数,对这些无限不循环小数进行命名,并定义. 学生活动:学生尝试对无理数下定义,并体会数系进一步扩充到实数范围. 探究新知 建构思维 思考:我们已经学习了实数的定义,接下来怎么学习实数呢?你能类比有理数的学习过程说一说吗? 学生活动:学生回忆有理数的学习过程并作答.
师:类比有理数的分类,请同学们尝试对实数进行分类. 学生活动:学生按照不同的分类标准对实数进行分类,体会用类比有理数的方法对实数展开学习. 师:每个有理数都可以用数轴上的点来表示,那无理数能否用数轴上的点来表示呢?你能在数轴上找到表示π的点吗? 师:请同学们自主探究用数轴上的点表示. 师:结合数轴我们可以研究实数之间的关系,比如大小关系,你能快速比较出刚才表示的这几个数的大小吗? 师:除了大小关系外,你从数轴上还发现了什么关系? 学生活动:学生体会实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.有理数的大小比较法则、相反数、绝对值的意义在实数范围内同样适用. 应用迁移 拓展思维 例题演练 例:(1)分别写出的相反数; (2)指出分别是什么数的相反数; (3)求的绝对值; (4)已知一个数的绝对值,求这个数. 学生活动:学生思考求相反数、绝对值的方法,规范书写,并进一步体会到相反数、绝对值的意义同样合适于实数. 例: 计算下列各式的值: (1); (2). 学生活动:学生体会在进行实数的加减运算时,有理数的运算法则、运算性质等同样适用. 生长拓学: 如图,一根细线上端固定,下端系一个小重物,让这个小重物来回自由摆动,来回摆动一次所用的时间t(单位:s)与细线的长度l(单位:m)之间满足关系.当细线的长度为0.2 m时,小重物来回摆动一次所用的时间是多少(结果保留小数点后一位)? 学生活动:学生体会用实数的运算解决实际问题,进一步增强应用数学的意识. 梳理小结 深化思维
