高考数学专题六解析几何 微专题38 圆锥曲线中二级结论的应用 课件(共56张PPT)
文档属性
| 名称 | 高考数学专题六解析几何 微专题38 圆锥曲线中二级结论的应用 课件(共56张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览











文档简介
(共56张PPT)
专题六 解析几何
微专题38
圆锥曲线中二级结论的应用
圆锥曲线是高中数学的重要内容之一,知识的综合性较强,因而解题时需要运用多种基础知识,采用多种数学手段,熟记各种定义、基本公式.法则固然很重要,但要做到迅速、准确地解题,还要掌握一些常用结论,正确灵活地运用这些结论,一些复杂的问题便能迎刃而解.
考情分析
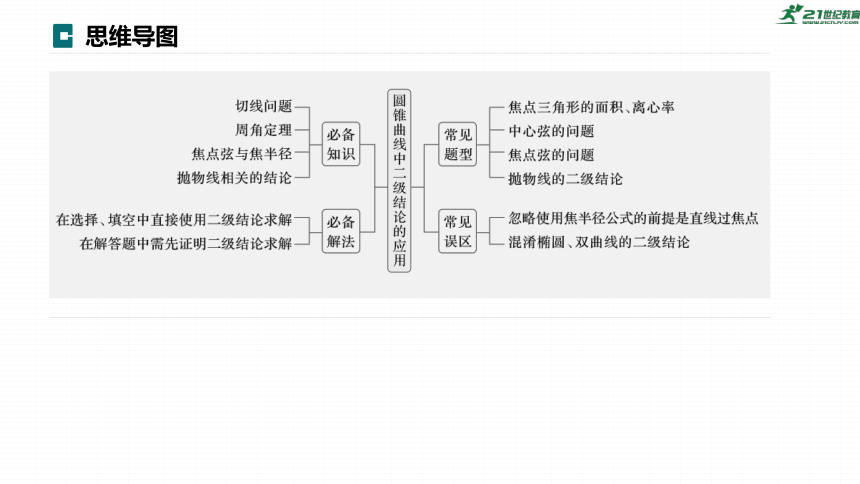
思维导图
内容索引
典型例题
热点突破
考点一 椭圆、双曲线的二级结论
(4)焦半径公式:设点P的坐标为(x0,y0),椭圆焦点在x轴上,则|PF1|=a+ex0,|PF2|=a-ex0.
(4)焦半径公式:设点P的坐标为(x0,y0),双曲线焦点在x轴上,则|PF1|=|a+ex0|,|PF2|=|a-ex0|.
典例1
跟踪训练1 (1)已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则点P到x轴的距离为
√
设P到x轴的距离为yP,
√
考点二 周角定理
典例2
√
√
椭圆的面积S=πab=6π,即ab=6, ①
因为点P为椭圆C的上顶点,所以P(0,b),
①②联立解得a=3,b=2.
所以椭圆C的短轴长为2b=4.
跟踪训练2
√
设P(x0,y0),Q(-x0,-y0)且x0≠±a,
1.焦点弦AB的长度表示(见图1)
(1)用A(x1,y1),B(x2,y2)的坐标表示:
对于抛物线y2=2px(p>0)而言:|AB|=x1+x2+p=2x0+p(其中x0为线段AB中点的横坐标).
对于抛物线x2=2py(p>0)而言:|AB|=y1+y2+p=2y0+p(其中y0为线段AB中点的纵坐标).
考点三 抛物线的二级结论
(2)用直线AB的倾斜角θ表示(见图2)
对于抛物线y2=2px(p>0)而言:
|AF|=|AC|=|GF|+|FH|=p+|AF|cos θ,
2.AB是抛物线y2=2px(p>0)过焦点F的弦,AC⊥l,BD⊥l,M是CD的中点.A(x1,y1),B(x2,y2),则有:(见图3)
(3)MF⊥AB.
(4)MA⊥MB.
(5)A,O,D三点共线.
(6)以AB为直径的圆与l相切.
3.M为抛物线y2=2px(p>0)的准线l上一点,MA,MB均与抛物线相切,A,B为切点,则有:(见图4)
(1)AB过焦点F.
(2)2yM=yA+yB.
(3)MA⊥MB.
(4)MF⊥AB.
典例3
√
(2)已知F是抛物线y2=2px(p>0)的焦点,过F作两条互相垂直的直线l1,l2,直线l1交抛物线于A,B两点,直线l2交抛物线于C,D两点,且|AB|·|CD|的最小值是64,则抛物线的方程为_________.
y2=4x
因为0所以当θ=45°时,|AB|·|CD|取得最小值16p2,
所以16p2=64,所以p=2,所以抛物线方程为y2=4x.
跟踪训练3 (1)抛物线y2=2px(p>0)的焦点为F,过焦点F且倾斜角为 的直线与抛物线相交于A,B两点,若|AB|=8,则抛物线的方程为
A.y2=4x B.y2=8x
C.y2=2x D.y2=6x
√
√
方法一 抛物线y2=4x的焦点为F(1,0),
设直线AB的方程为x=ty+1,A(x1,y1),B(x2,y2),
Δ=16t2+16>0恒成立,
方法二 因为AB过抛物线的焦点,
设A(x1,y1),B(x2,y2),
圆锥曲线有许多形式结构相当漂亮的结论,记住圆锥曲线中一些二级结论,能快速解决圆锥曲线压轴小题,常用结论包括椭圆与双曲线中的焦点三角形面积公式、焦半径、切线方程、离心率等,周角定理以及抛物线焦点弦二级结论的综合应用.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
设|PF1|=m,|PF2|=n,由椭圆定义知m+n=2a,
在△F1PF2中,由余弦定理得4c2=m2+n2-2mncos∠F1PF2=(m+n)2-3mn=4a2-3mn,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
2.已知双曲线E的中心为原点,F(1,0)是E的焦点,过F的直线l与E相交于A,B两点且AB的中点为N(-4,-5),则双曲线E的渐近线的方程为
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
设B为短轴端点,则 =b2tan 45°=b2≤ =bc,
∵a>b>0,∴b≤c,即b2≤c2,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
不妨设直线l1的倾斜角小于直线l2的倾斜角,
1
2
3
4
5
6
7
8
9
10
11
12
所以0≤sin 2θ≤1,所以8≤8+sin22θ≤9,
1
2
3
4
5
6
7
8
9
10
11
12
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
对于B,△F1PF2的周长为|PF1|+|PF2|+|F1F2|=2a+2c=18,故B正确;
1
2
3
4
5
6
7
8
9
10
11
12
8.(多选)已知抛物线E:y2=4x的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,则下列结论正确的是
A.若直线AB的倾斜角为45°,则|AB|=8
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
若直线AB的倾斜角为45°,
设直线AB的倾斜角为θ,
1
2
3
4
5
6
7
8
9
10
11
12
设A(x1,y1),B(x2,y2),则C(-1,y1),
故B,O,C三点共线,故C正确;
设C(-1,y1),D(-1,y2),F(1,0),
故CF⊥DF,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
10.设F为抛物线C:y2=16x的焦点,过点F且倾斜角为 的直线交C于A,B两点,O为坐标原点,则△AOB的面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
64
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
12.已知抛物线C:y2=16x的焦点为F,直线x-my-4=0(m∈R)与抛物线C交于A,B两点,则|AF|+4|BF|的最小值是______.
36
方法一 设A(x1,y1),B(x2,y2),由抛物线的定义,知
|AF|=x1+4,|BF|=x2+4,
化简得x2-(16m2+8)x+16=0,
由根与系数的关系得x1x2=16,
当且仅当x1=4x2,即x1=8,x2=2时等号成立,
∴|AF|+4|BF|的最小值为36.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
方法二 抛物线的焦点F(4,0)在直线x-my-4=0上,
1
2
3
4
5
6
7
8
9
10
11
12
即|AF|=12,|BF|=6时等号成立,
∴(|AF|+4|BF|)min=36.
专题六 解析几何
微专题38
圆锥曲线中二级结论的应用
圆锥曲线是高中数学的重要内容之一,知识的综合性较强,因而解题时需要运用多种基础知识,采用多种数学手段,熟记各种定义、基本公式.法则固然很重要,但要做到迅速、准确地解题,还要掌握一些常用结论,正确灵活地运用这些结论,一些复杂的问题便能迎刃而解.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 椭圆、双曲线的二级结论
(4)焦半径公式:设点P的坐标为(x0,y0),椭圆焦点在x轴上,则|PF1|=a+ex0,|PF2|=a-ex0.
(4)焦半径公式:设点P的坐标为(x0,y0),双曲线焦点在x轴上,则|PF1|=|a+ex0|,|PF2|=|a-ex0|.
典例1
跟踪训练1 (1)已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则点P到x轴的距离为
√
设P到x轴的距离为yP,
√
考点二 周角定理
典例2
√
√
椭圆的面积S=πab=6π,即ab=6, ①
因为点P为椭圆C的上顶点,所以P(0,b),
①②联立解得a=3,b=2.
所以椭圆C的短轴长为2b=4.
跟踪训练2
√
设P(x0,y0),Q(-x0,-y0)且x0≠±a,
1.焦点弦AB的长度表示(见图1)
(1)用A(x1,y1),B(x2,y2)的坐标表示:
对于抛物线y2=2px(p>0)而言:|AB|=x1+x2+p=2x0+p(其中x0为线段AB中点的横坐标).
对于抛物线x2=2py(p>0)而言:|AB|=y1+y2+p=2y0+p(其中y0为线段AB中点的纵坐标).
考点三 抛物线的二级结论
(2)用直线AB的倾斜角θ表示(见图2)
对于抛物线y2=2px(p>0)而言:
|AF|=|AC|=|GF|+|FH|=p+|AF|cos θ,
2.AB是抛物线y2=2px(p>0)过焦点F的弦,AC⊥l,BD⊥l,M是CD的中点.A(x1,y1),B(x2,y2),则有:(见图3)
(3)MF⊥AB.
(4)MA⊥MB.
(5)A,O,D三点共线.
(6)以AB为直径的圆与l相切.
3.M为抛物线y2=2px(p>0)的准线l上一点,MA,MB均与抛物线相切,A,B为切点,则有:(见图4)
(1)AB过焦点F.
(2)2yM=yA+yB.
(3)MA⊥MB.
(4)MF⊥AB.
典例3
√
(2)已知F是抛物线y2=2px(p>0)的焦点,过F作两条互相垂直的直线l1,l2,直线l1交抛物线于A,B两点,直线l2交抛物线于C,D两点,且|AB|·|CD|的最小值是64,则抛物线的方程为_________.
y2=4x
因为0
所以16p2=64,所以p=2,所以抛物线方程为y2=4x.
跟踪训练3 (1)抛物线y2=2px(p>0)的焦点为F,过焦点F且倾斜角为 的直线与抛物线相交于A,B两点,若|AB|=8,则抛物线的方程为
A.y2=4x B.y2=8x
C.y2=2x D.y2=6x
√
√
方法一 抛物线y2=4x的焦点为F(1,0),
设直线AB的方程为x=ty+1,A(x1,y1),B(x2,y2),
Δ=16t2+16>0恒成立,
方法二 因为AB过抛物线的焦点,
设A(x1,y1),B(x2,y2),
圆锥曲线有许多形式结构相当漂亮的结论,记住圆锥曲线中一些二级结论,能快速解决圆锥曲线压轴小题,常用结论包括椭圆与双曲线中的焦点三角形面积公式、焦半径、切线方程、离心率等,周角定理以及抛物线焦点弦二级结论的综合应用.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
设|PF1|=m,|PF2|=n,由椭圆定义知m+n=2a,
在△F1PF2中,由余弦定理得4c2=m2+n2-2mncos∠F1PF2=(m+n)2-3mn=4a2-3mn,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
2.已知双曲线E的中心为原点,F(1,0)是E的焦点,过F的直线l与E相交于A,B两点且AB的中点为N(-4,-5),则双曲线E的渐近线的方程为
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
设B为短轴端点,则 =b2tan 45°=b2≤ =bc,
∵a>b>0,∴b≤c,即b2≤c2,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
不妨设直线l1的倾斜角小于直线l2的倾斜角,
1
2
3
4
5
6
7
8
9
10
11
12
所以0≤sin 2θ≤1,所以8≤8+sin22θ≤9,
1
2
3
4
5
6
7
8
9
10
11
12
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
对于B,△F1PF2的周长为|PF1|+|PF2|+|F1F2|=2a+2c=18,故B正确;
1
2
3
4
5
6
7
8
9
10
11
12
8.(多选)已知抛物线E:y2=4x的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,则下列结论正确的是
A.若直线AB的倾斜角为45°,则|AB|=8
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
若直线AB的倾斜角为45°,
设直线AB的倾斜角为θ,
1
2
3
4
5
6
7
8
9
10
11
12
设A(x1,y1),B(x2,y2),则C(-1,y1),
故B,O,C三点共线,故C正确;
设C(-1,y1),D(-1,y2),F(1,0),
故CF⊥DF,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
10.设F为抛物线C:y2=16x的焦点,过点F且倾斜角为 的直线交C于A,B两点,O为坐标原点,则△AOB的面积为______.
1
2
3
4
5
6
7
8
9
10
11
12
64
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
12.已知抛物线C:y2=16x的焦点为F,直线x-my-4=0(m∈R)与抛物线C交于A,B两点,则|AF|+4|BF|的最小值是______.
36
方法一 设A(x1,y1),B(x2,y2),由抛物线的定义,知
|AF|=x1+4,|BF|=x2+4,
化简得x2-(16m2+8)x+16=0,
由根与系数的关系得x1x2=16,
当且仅当x1=4x2,即x1=8,x2=2时等号成立,
∴|AF|+4|BF|的最小值为36.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
方法二 抛物线的焦点F(4,0)在直线x-my-4=0上,
1
2
3
4
5
6
7
8
9
10
11
12
即|AF|=12,|BF|=6时等号成立,
∴(|AF|+4|BF|)min=36.
同课章节目录
