高考数学专题六解析几何 微专题37 离心率的范围问题 课件(共62张PPT)
文档属性
| 名称 | 高考数学专题六解析几何 微专题37 离心率的范围问题 课件(共62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 23:59:00 | ||
图片预览









文档简介
(共62张PPT)
专题六 解析几何
微专题37
离心率的范围问题
圆锥曲线离心率的范围问题是高考的热点题型,对圆锥曲线中已知特征关系的转化是解决此类问题的关键,相关平面几何关系的挖掘应用也可使问题求解更简洁.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1
考点一 利用圆锥曲线的定义求离心率
√
假设|MF1|>|MF2|,
所以由椭圆、双曲线定义得
所以在△MF1F2中,|F1F2|=2c,由余弦定理得
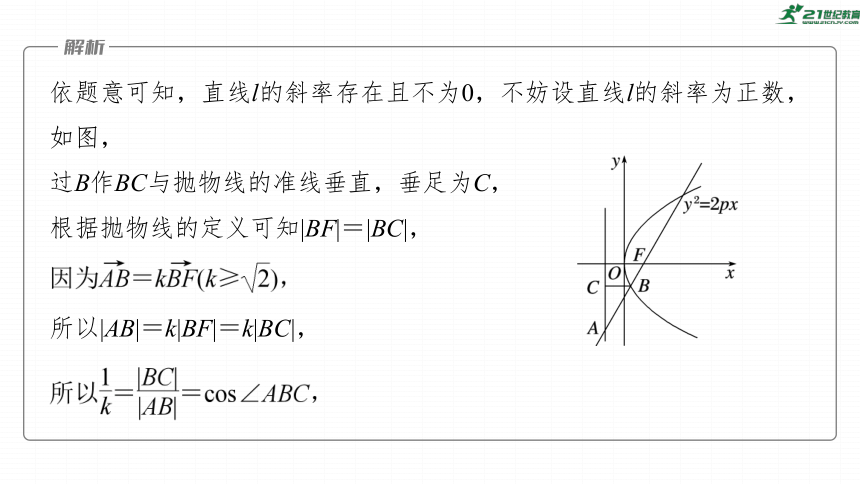
依题意可知,直线l的斜率存在且不为0,不妨设直线l的斜率为正数,如图,
过B作BC与抛物线的准线垂直,垂足为C,
根据抛物线的定义可知|BF|=|BC|,
所以|AB|=k|BF|=k|BC|,
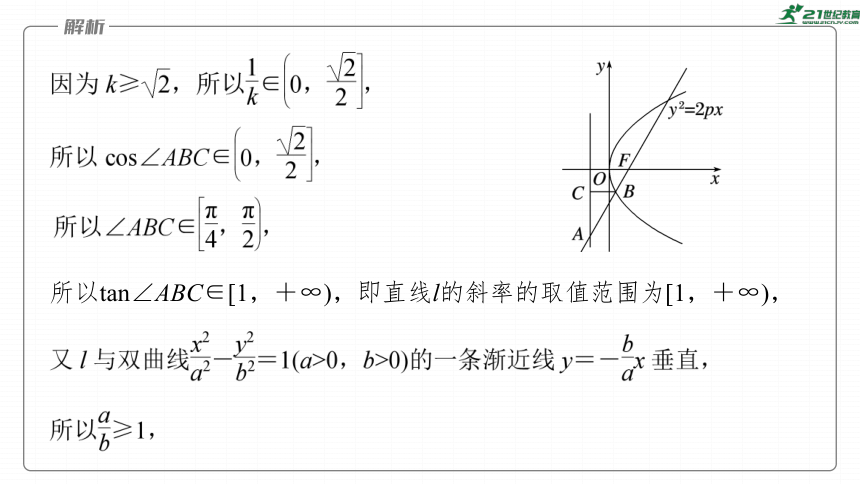
所以tan∠ABC∈[1,+∞),即直线l的斜率的取值范围为[1,+∞),
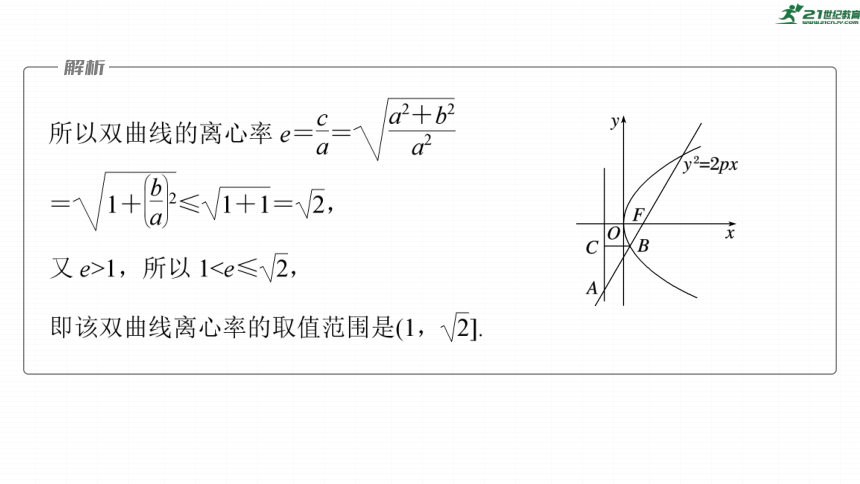
跟踪训练1
√
√
由已知可得|MF2|-|MF1|=2a,若|MF2|+|MN|>4b,
即|MF1|+|MN|+2a>4b,左支上的点M均满足|MF2|+|MN|>4b,
如图所示,当点M位于H点时,|MF1|+|MN|最小,
∴3b2-8ab+4a2>0,
∴(2a-b)(2a-3b)>0,
∴2a>3b或2a∴4a2>9b2或4a2典例2 (1)已知双曲线 (a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则双曲线的离心率的取值范围是___________.
考点二 利用圆锥曲线的性质求离心率范围
[2,+∞)
依题意,不妨设P点为双曲线的右支上的一点,F1为左焦点,F2为右焦点,
整理得c2-2ac-a2<0,
跟踪训练2
√
不妨设P(3,t)(t>0),F1(-c,0),F2(c,0),
设直线PF1倾斜角为α,直线PF2倾斜角为β,
考点三 利用几何图形的性质求离心率范围
典例3 (1)(2023·重庆模拟)已知P为圆C:x2+y2-6y=40上一点,椭圆M:
(a>b>0)的焦距为6,点P关于直线x-y=0的对称点在椭圆M上,
则椭圆离心率的取值范围为________.
圆C:x2+(y-3)2=49关于直线x-y=0对称的圆为(x-3)2+y2=49,
又椭圆的右焦点(3,0)是圆的圆心,
所以a+c≥7,且a-c≤7,
又c=3,
√
设以F2(c,0)圆心,a为半径的圆与双曲线的一条渐近线bx-ay=0交于A,B两点,
可得4a2-4b2>c2=a2+b2,
即3a2>5b2=5c2-5a2,可得5c2<8a2,
跟踪训练3 (1)已知椭圆C: (a>b>0)的左焦点为F,经过原点的直线与C交于A,B两点,若∠AFB≥150°,则C的离心率的取值范围为
________________.
如图,设椭圆的右焦点为F′,连接AF′,BF′,
∵AB,FF′互相平分,
∴四边形AF′BF为平行四边形,
∴∠AFB+∠FBF′=180°,
∵∠AFB≥150°,∴∠FBF′≤30°,
由条件知,当B在短轴端点(不妨取上端点B1)时,∠FBF′最大,
此时在Rt△B1OF′中,∠OB1F′=15°,
(2)已知F1,F2分别为双曲线的左、右焦点,O为坐标原点,以原点为圆心,|OF1|为半径的圆与双曲线左支的一个交点为P,若PF1与双曲线右支有交点,则双曲线的离心率的取值范围为_____________.
设直线PF1的方程为y=k(x+c),即kx-y+kc=0,
化简可得b>2a,即有b2>4a2,
关于圆锥曲线离心率(范围)问题处理的主体思想是:建立一个关于a,b,c的方程(或不等式).一般建立方程有两种方法:(1)利用圆锥曲线的定义解决;(2)利用题中的几何关系来解决问题.另外,不能忽略了圆锥曲线离心率的自身限制条件.
总结提升
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
2.如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2为椭圆的顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PB2为钝角,则该椭圆的离心率的取值范围是
√
1
2
3
4
5
6
7
8
设B1(0,-b),B2(0,b),F2(c,0),A2(a,0).
即a2-c2-ac>0.
两边同时除以a2并化简得e2+e-1<0,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
5.(2023·咸宁模拟)已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=24,椭圆与双曲线的离心率分别为e1,e2,则3e1e2的取值范围是
√
1
2
3
4
5
6
7
8
设椭圆与双曲线的半焦距为c,椭圆长半轴长为a1,双曲线实半轴长为a2,|PF1|=r1=24,|PF2|=r2,
∵△PF1F2是以PF1为底边的等腰三角形,点P在第一象限内,
∴|PF2|=|F1F2|,|PF1|>|PF2|,|PF2|+|F1F2|>|PF1|,
即r2=2c,r1>r2,2r2>r1,
∴2c<24,4c>24,解得6在双曲线中,|PF1|-|PF2|=2a2,
1
2
3
4
5
6
7
8
在椭圆中,|PF1|+|PF2|=2a1,
∵6∴3e1e2的取值范围为(1,+∞).
1
2
3
4
5
6
7
8
√
√
1
2
3
4
5
6
7
8
如图,设|MF1|=m,|MF2|=n,焦距为2c,
由椭圆定义可得m+n=2a,
由双曲线定义可得m-n=2a1,
解得m=a+a1,n=a-a1,
当|F1F2|=2|MO|时,则∠F1MF2=90°,
所以m2+n2=4c2,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
记双曲线C的右焦点为F2,∴|F2B|=2a+λb,
∵△OF1A为直角三角形,
1
2
3
4
5
6
7
8
∴a21
2
3
4
5
6
7
8
8.如图所示,底面半径为3,高为8的圆柱内放有一个半径为3的球,球与圆柱下底面相切,作不与圆柱底面平行的平面α与球相切于点F,若平面α与圆柱侧面相交所得曲线为封闭曲线C,且C是以F为一个焦点的椭圆,则C的离心率的
最大值为_____.
1
2
3
4
5
6
7
8
当α与底面趋于平行时,椭圆C几乎成为一个圆,
因此离心率可以充分接近0.
当α与底面的夹角最大时,椭圆C的离心率达到最大,
下面求解这一最大值.
如图,A,B为长轴,F为焦点时,e最大.
a+c=|BF|=|BG|=8-3=5,易知b=3,
又a2-c2=9,
1
2
3
4
5
6
7
8
专题六 解析几何
微专题37
离心率的范围问题
圆锥曲线离心率的范围问题是高考的热点题型,对圆锥曲线中已知特征关系的转化是解决此类问题的关键,相关平面几何关系的挖掘应用也可使问题求解更简洁.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1
考点一 利用圆锥曲线的定义求离心率
√
假设|MF1|>|MF2|,
所以由椭圆、双曲线定义得
所以在△MF1F2中,|F1F2|=2c,由余弦定理得
依题意可知,直线l的斜率存在且不为0,不妨设直线l的斜率为正数,如图,
过B作BC与抛物线的准线垂直,垂足为C,
根据抛物线的定义可知|BF|=|BC|,
所以|AB|=k|BF|=k|BC|,
所以tan∠ABC∈[1,+∞),即直线l的斜率的取值范围为[1,+∞),
跟踪训练1
√
√
由已知可得|MF2|-|MF1|=2a,若|MF2|+|MN|>4b,
即|MF1|+|MN|+2a>4b,左支上的点M均满足|MF2|+|MN|>4b,
如图所示,当点M位于H点时,|MF1|+|MN|最小,
∴3b2-8ab+4a2>0,
∴(2a-b)(2a-3b)>0,
∴2a>3b或2a
考点二 利用圆锥曲线的性质求离心率范围
[2,+∞)
依题意,不妨设P点为双曲线的右支上的一点,F1为左焦点,F2为右焦点,
整理得c2-2ac-a2<0,
跟踪训练2
√
不妨设P(3,t)(t>0),F1(-c,0),F2(c,0),
设直线PF1倾斜角为α,直线PF2倾斜角为β,
考点三 利用几何图形的性质求离心率范围
典例3 (1)(2023·重庆模拟)已知P为圆C:x2+y2-6y=40上一点,椭圆M:
(a>b>0)的焦距为6,点P关于直线x-y=0的对称点在椭圆M上,
则椭圆离心率的取值范围为________.
圆C:x2+(y-3)2=49关于直线x-y=0对称的圆为(x-3)2+y2=49,
又椭圆的右焦点(3,0)是圆的圆心,
所以a+c≥7,且a-c≤7,
又c=3,
√
设以F2(c,0)圆心,a为半径的圆与双曲线的一条渐近线bx-ay=0交于A,B两点,
可得4a2-4b2>c2=a2+b2,
即3a2>5b2=5c2-5a2,可得5c2<8a2,
跟踪训练3 (1)已知椭圆C: (a>b>0)的左焦点为F,经过原点的直线与C交于A,B两点,若∠AFB≥150°,则C的离心率的取值范围为
________________.
如图,设椭圆的右焦点为F′,连接AF′,BF′,
∵AB,FF′互相平分,
∴四边形AF′BF为平行四边形,
∴∠AFB+∠FBF′=180°,
∵∠AFB≥150°,∴∠FBF′≤30°,
由条件知,当B在短轴端点(不妨取上端点B1)时,∠FBF′最大,
此时在Rt△B1OF′中,∠OB1F′=15°,
(2)已知F1,F2分别为双曲线的左、右焦点,O为坐标原点,以原点为圆心,|OF1|为半径的圆与双曲线左支的一个交点为P,若PF1与双曲线右支有交点,则双曲线的离心率的取值范围为_____________.
设直线PF1的方程为y=k(x+c),即kx-y+kc=0,
化简可得b>2a,即有b2>4a2,
关于圆锥曲线离心率(范围)问题处理的主体思想是:建立一个关于a,b,c的方程(或不等式).一般建立方程有两种方法:(1)利用圆锥曲线的定义解决;(2)利用题中的几何关系来解决问题.另外,不能忽略了圆锥曲线离心率的自身限制条件.
总结提升
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
2.如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2为椭圆的顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PB2为钝角,则该椭圆的离心率的取值范围是
√
1
2
3
4
5
6
7
8
设B1(0,-b),B2(0,b),F2(c,0),A2(a,0).
即a2-c2-ac>0.
两边同时除以a2并化简得e2+e-1<0,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
5.(2023·咸宁模拟)已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=24,椭圆与双曲线的离心率分别为e1,e2,则3e1e2的取值范围是
√
1
2
3
4
5
6
7
8
设椭圆与双曲线的半焦距为c,椭圆长半轴长为a1,双曲线实半轴长为a2,|PF1|=r1=24,|PF2|=r2,
∵△PF1F2是以PF1为底边的等腰三角形,点P在第一象限内,
∴|PF2|=|F1F2|,|PF1|>|PF2|,|PF2|+|F1F2|>|PF1|,
即r2=2c,r1>r2,2r2>r1,
∴2c<24,4c>24,解得6
1
2
3
4
5
6
7
8
在椭圆中,|PF1|+|PF2|=2a1,
∵6
1
2
3
4
5
6
7
8
√
√
1
2
3
4
5
6
7
8
如图,设|MF1|=m,|MF2|=n,焦距为2c,
由椭圆定义可得m+n=2a,
由双曲线定义可得m-n=2a1,
解得m=a+a1,n=a-a1,
当|F1F2|=2|MO|时,则∠F1MF2=90°,
所以m2+n2=4c2,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
记双曲线C的右焦点为F2,∴|F2B|=2a+λb,
∵△OF1A为直角三角形,
1
2
3
4
5
6
7
8
∴a2
2
3
4
5
6
7
8
8.如图所示,底面半径为3,高为8的圆柱内放有一个半径为3的球,球与圆柱下底面相切,作不与圆柱底面平行的平面α与球相切于点F,若平面α与圆柱侧面相交所得曲线为封闭曲线C,且C是以F为一个焦点的椭圆,则C的离心率的
最大值为_____.
1
2
3
4
5
6
7
8
当α与底面趋于平行时,椭圆C几乎成为一个圆,
因此离心率可以充分接近0.
当α与底面的夹角最大时,椭圆C的离心率达到最大,
下面求解这一最大值.
如图,A,B为长轴,F为焦点时,e最大.
a+c=|BF|=|BG|=8-3=5,易知b=3,
又a2-c2=9,
1
2
3
4
5
6
7
8
同课章节目录
