高考数学专题六解析几何 微专题42 证明性、探究性问题 课件(共60张PPT)
文档属性
| 名称 | 高考数学专题六解析几何 微专题42 证明性、探究性问题 课件(共60张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览




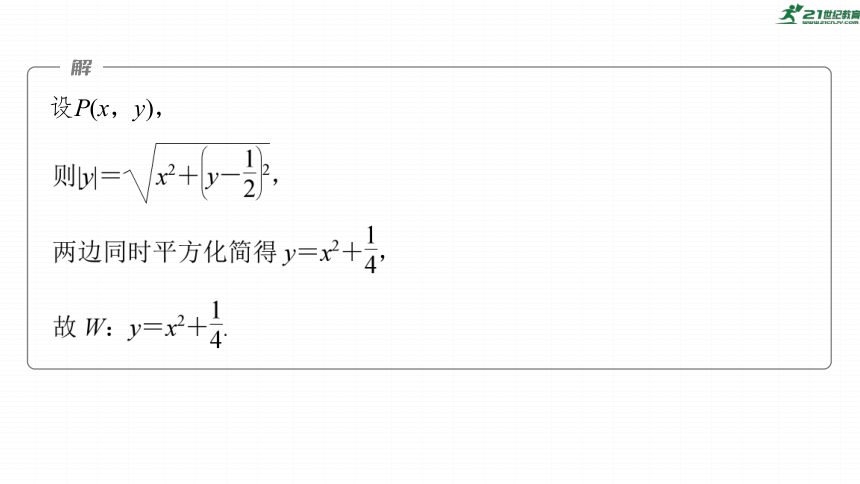





文档简介
(共60张PPT)
专题六 解析几何
微专题42
证明性、探究性问题
圆锥曲线的综合问题是高考考查的重点内容,证明性、探索性问题是常见的热点题型,常以解答题的形式压轴出现,难度较大.
考情分析
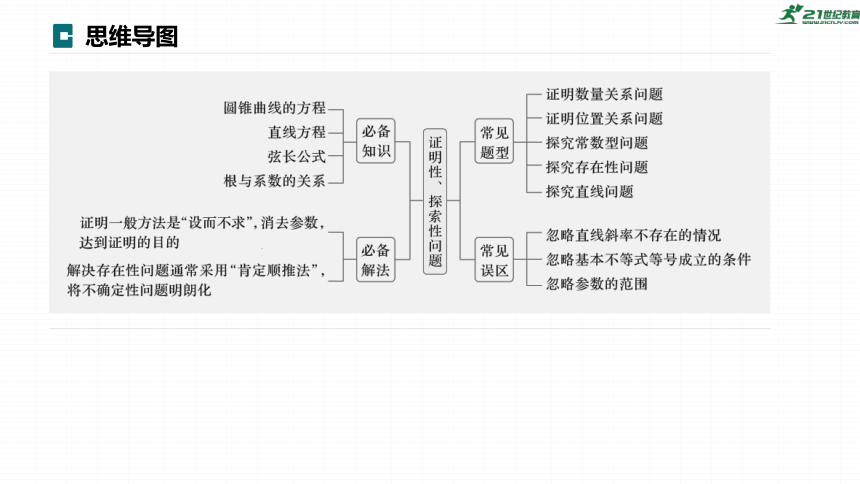
思维导图
内容索引
典型例题
热点突破
典例1 (2023·新高考全国Ⅰ)在直角坐标系Oxy中,点P到x轴的距离等于点P到点 的距离,记动点P的轨迹为W.
(1)求W的方程;
考点一 圆锥曲线的证明性问题
设P(x,y),
易知矩形四条边所在直线的斜率均存在,且不为0,
则kAB·kBC=-1,a+b同理令kBC=b+c=n>0,且mn=-1,
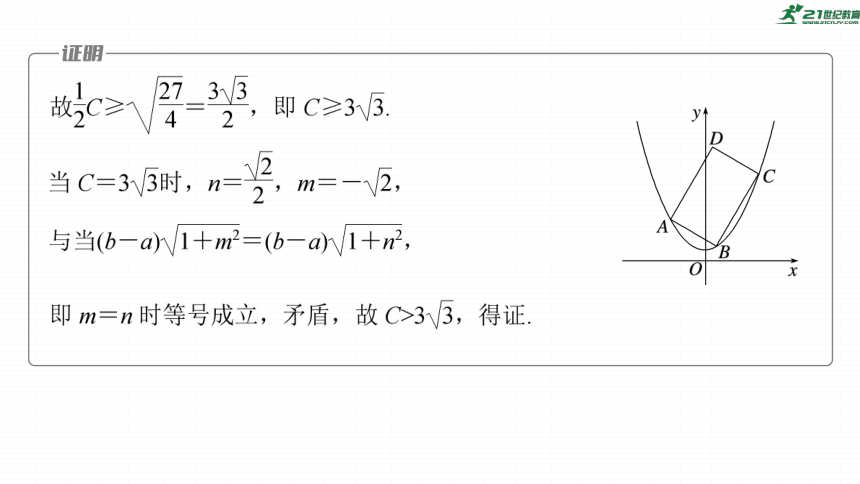
设矩形周长为C,由对称性不妨设|m|≥|n|,
方法二 不妨设A,B,D在W上,且BA⊥DA,
易知直线BA,DA的斜率均存在且不为0,
得x2-kx+ka-a2=0,
Δ=k2-4(ka-a2)=(k-2a)2>0,则k≠2a,
令k2=m,则m∈(0,1],
矩形ABCD变换为矩形A′B′C′D′,
则kA′B′=t1+t0,kB′C′=t2+t0,
由于A′B′⊥B′C′,
则(t1+t0)(t2+t0)=-1.
令t2+t0=tan θ,
则t2=tan θ-t0,t1=-cot θ-t0,从而
由于t1从而-cot θ-t0又t0≥0,
跟踪训练1
所以双曲线C的方程为x2-y2=a2,
因为l1与双曲线C仅有一个公共点,
所以Δ=162-4(a2+48)=0,解得a2=16,
(2)设双曲线C的左顶点为A,直线l2平行于l1,且交双曲线C于M,N两点,求证:△AMN的垂心在双曲线C上.
消去y得3x2+4mx+m2+16=0,
如图所示,过A引MN的垂线交C于另一点H,
即AH⊥MN,连接MH,
所以MH⊥AN,故H为△AMN的垂心,得证.
典例2
考点二 圆锥曲线的探究性问题
由椭圆的定义可得△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a=8,
存在.由题意可知,直线n的斜率不为0,其方程可设为x=my+1,
设M(x1,y1),N(x2,y2),则P(4,y1),Q(4,y2),
可得(m2+4)y2+2my-3=0,Δ=4m2+12(m2+4)=16(m2+3)>0,
跟踪训练2 (2023·日照模拟)已知抛物线C:x2=2py(p>0)的焦点为F,E为C上的动点,EQ垂直于动直线y=t(t<0),垂足为Q,当△EQF为等边三角形时,其面积为 .
(1)求C的方程;
∴C的方程为x2=4y.
(2)设O为原点,过点E的直线l与C相切,且与椭圆 交于A,B两点,直线OQ与AB交于点M,试问是否存在t,使得|AM|=|BM|?若存在,求t的值;若不存在,请说明理由.
假设存在t,使得|AM|=|BM|,则M为线段AB的中点,
综上,存在t,使得|AM|=|BM|,此时t的值为-1.
证明性问题主要根据直线与圆锥曲线的性质、直线与圆锥曲线的位置关系等,通过相关性质的应用、代数式的恒等变形以及必要的数值计算等进行证明.
存在性问题通常采用“肯定顺推法”,将不确定的问题明朗化.其步骤为假设满足条件的元素(点、直线、曲线或参数)存在并设出,列出关于待定系数的方程(组),若方程(组)有实数解,则元素(点、直线、曲线或参数)存在;否则,元素(点、直线、曲线或参数)不存在.注意:当结论或条件不唯一时,要分类讨论.
总结提升
1
2
3
1.(2023·湖南师大附中模拟)如图,椭圆C:
(a>2),圆O:x2+y2=a2+4,椭圆C的左、右焦点分别为F1,F2.
(1)过椭圆上一点P和原点O作直线l交圆O于M,N两点,若|PF1|·|PF2|=6,求|PM|·|PN|的值;
1
2
3
设P(x0,y0),由于|PF1|+|PF2|=2a |PF1|2+|PF2|2+2|PF1|·|PF2|=4a2,
而|PF1|·|PF2|=6,
=a2+4-(a2-2)=6.
1
2
3
(2)过圆O上任意点R引椭圆C的两条切线,求证:两条切线互相垂直.
1
2
3
设R(m,n),则m2+n2=a2+4,即n2-4=a2-m2,
设过点R的圆O的切线斜率都存在时的方程为
y=k(x-m)+n(m2≠a2),代入椭圆方程得
整理得(4+a2k2)x2-2ka2(km-n)x+a2(km-n)2-4a2=0,
即(km-n)2-a2k2-4=0 (m2-a2)k2-2mnk+n2-4=0,
1
2
3
即两条切线的斜率都存在时,有两条切线互相垂直;
而当过R的切线斜率不存在时,易知R点的坐标为
(±a,±2),
此时显然两条切线互相垂直,
综上,过圆O上任意点R引椭圆C的两条切线,则两条切线互相垂直.
1
2
3
1
2
3
1
2
3
(2)设点O(0,0),M(0,2),动直线l:y=kx+m与C的右支相交于不同两点A,B,且∠AFM=∠BFM,过点O作OH⊥l,H为垂足,证明:动点H在定圆上,并求该圆的方程.
1
2
3
由∠AFM=∠BFM,
得cos∠AFM=cos∠BFM,
1
2
3
整理得(2m+k+3)(x1-x2)=0,
因为x1≠x2,所以2m+k+3=0,
1
2
3
又因为OH⊥l,垂足为H,所以动点H在以ON为直径的圆上,
1
2
3
1
2
3
1
2
3
(2)设MN与x轴交于点T,是否存在点P使得xP=4xT(其中xP,xT分别为点P,T的横坐标)?若存在,求出点P的坐标;若不存在,请说明理由.
1
2
3
方法一 设P(x0,t),M(x1,y1),N(x2,y2),A(-2,0),B(2,0),
令xT=n(-21
2
3
易得Δ>0,
1
2
3
若存在xP=4xT,即x0=4n,
又P在第一象限,所以n=1,P(4,3).
1
2
3
方法二 设P(x0,y0),M(x1,y1),N(x2,y2),A(-2,0),B(2,0),
1
2
3
1
2
3
而P在第一象限,所以x0=4,即P(4,3).
专题六 解析几何
微专题42
证明性、探究性问题
圆锥曲线的综合问题是高考考查的重点内容,证明性、探索性问题是常见的热点题型,常以解答题的形式压轴出现,难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (2023·新高考全国Ⅰ)在直角坐标系Oxy中,点P到x轴的距离等于点P到点 的距离,记动点P的轨迹为W.
(1)求W的方程;
考点一 圆锥曲线的证明性问题
设P(x,y),
易知矩形四条边所在直线的斜率均存在,且不为0,
则kAB·kBC=-1,a+b
设矩形周长为C,由对称性不妨设|m|≥|n|,
方法二 不妨设A,B,D在W上,且BA⊥DA,
易知直线BA,DA的斜率均存在且不为0,
得x2-kx+ka-a2=0,
Δ=k2-4(ka-a2)=(k-2a)2>0,则k≠2a,
令k2=m,则m∈(0,1],
矩形ABCD变换为矩形A′B′C′D′,
则kA′B′=t1+t0,kB′C′=t2+t0,
由于A′B′⊥B′C′,
则(t1+t0)(t2+t0)=-1.
令t2+t0=tan θ,
则t2=tan θ-t0,t1=-cot θ-t0,从而
由于t1
跟踪训练1
所以双曲线C的方程为x2-y2=a2,
因为l1与双曲线C仅有一个公共点,
所以Δ=162-4(a2+48)=0,解得a2=16,
(2)设双曲线C的左顶点为A,直线l2平行于l1,且交双曲线C于M,N两点,求证:△AMN的垂心在双曲线C上.
消去y得3x2+4mx+m2+16=0,
如图所示,过A引MN的垂线交C于另一点H,
即AH⊥MN,连接MH,
所以MH⊥AN,故H为△AMN的垂心,得证.
典例2
考点二 圆锥曲线的探究性问题
由椭圆的定义可得△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a=8,
存在.由题意可知,直线n的斜率不为0,其方程可设为x=my+1,
设M(x1,y1),N(x2,y2),则P(4,y1),Q(4,y2),
可得(m2+4)y2+2my-3=0,Δ=4m2+12(m2+4)=16(m2+3)>0,
跟踪训练2 (2023·日照模拟)已知抛物线C:x2=2py(p>0)的焦点为F,E为C上的动点,EQ垂直于动直线y=t(t<0),垂足为Q,当△EQF为等边三角形时,其面积为 .
(1)求C的方程;
∴C的方程为x2=4y.
(2)设O为原点,过点E的直线l与C相切,且与椭圆 交于A,B两点,直线OQ与AB交于点M,试问是否存在t,使得|AM|=|BM|?若存在,求t的值;若不存在,请说明理由.
假设存在t,使得|AM|=|BM|,则M为线段AB的中点,
综上,存在t,使得|AM|=|BM|,此时t的值为-1.
证明性问题主要根据直线与圆锥曲线的性质、直线与圆锥曲线的位置关系等,通过相关性质的应用、代数式的恒等变形以及必要的数值计算等进行证明.
存在性问题通常采用“肯定顺推法”,将不确定的问题明朗化.其步骤为假设满足条件的元素(点、直线、曲线或参数)存在并设出,列出关于待定系数的方程(组),若方程(组)有实数解,则元素(点、直线、曲线或参数)存在;否则,元素(点、直线、曲线或参数)不存在.注意:当结论或条件不唯一时,要分类讨论.
总结提升
1
2
3
1.(2023·湖南师大附中模拟)如图,椭圆C:
(a>2),圆O:x2+y2=a2+4,椭圆C的左、右焦点分别为F1,F2.
(1)过椭圆上一点P和原点O作直线l交圆O于M,N两点,若|PF1|·|PF2|=6,求|PM|·|PN|的值;
1
2
3
设P(x0,y0),由于|PF1|+|PF2|=2a |PF1|2+|PF2|2+2|PF1|·|PF2|=4a2,
而|PF1|·|PF2|=6,
=a2+4-(a2-2)=6.
1
2
3
(2)过圆O上任意点R引椭圆C的两条切线,求证:两条切线互相垂直.
1
2
3
设R(m,n),则m2+n2=a2+4,即n2-4=a2-m2,
设过点R的圆O的切线斜率都存在时的方程为
y=k(x-m)+n(m2≠a2),代入椭圆方程得
整理得(4+a2k2)x2-2ka2(km-n)x+a2(km-n)2-4a2=0,
即(km-n)2-a2k2-4=0 (m2-a2)k2-2mnk+n2-4=0,
1
2
3
即两条切线的斜率都存在时,有两条切线互相垂直;
而当过R的切线斜率不存在时,易知R点的坐标为
(±a,±2),
此时显然两条切线互相垂直,
综上,过圆O上任意点R引椭圆C的两条切线,则两条切线互相垂直.
1
2
3
1
2
3
1
2
3
(2)设点O(0,0),M(0,2),动直线l:y=kx+m与C的右支相交于不同两点A,B,且∠AFM=∠BFM,过点O作OH⊥l,H为垂足,证明:动点H在定圆上,并求该圆的方程.
1
2
3
由∠AFM=∠BFM,
得cos∠AFM=cos∠BFM,
1
2
3
整理得(2m+k+3)(x1-x2)=0,
因为x1≠x2,所以2m+k+3=0,
1
2
3
又因为OH⊥l,垂足为H,所以动点H在以ON为直径的圆上,
1
2
3
1
2
3
1
2
3
(2)设MN与x轴交于点T,是否存在点P使得xP=4xT(其中xP,xT分别为点P,T的横坐标)?若存在,求出点P的坐标;若不存在,请说明理由.
1
2
3
方法一 设P(x0,t),M(x1,y1),N(x2,y2),A(-2,0),B(2,0),
令xT=n(-2
2
3
易得Δ>0,
1
2
3
若存在xP=4xT,即x0=4n,
又P在第一象限,所以n=1,P(4,3).
1
2
3
方法二 设P(x0,y0),M(x1,y1),N(x2,y2),A(-2,0),B(2,0),
1
2
3
1
2
3
而P在第一象限,所以x0=4,即P(4,3).
同课章节目录
