高考数学专题三数列 微专题21 等差数列、等比数列 课件(共58张PPT)
文档属性
| 名称 | 高考数学专题三数列 微专题21 等差数列、等比数列 课件(共58张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览




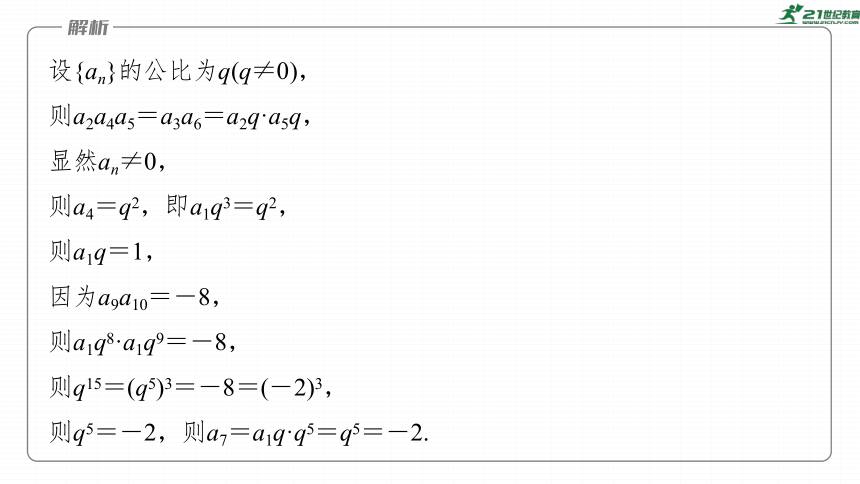



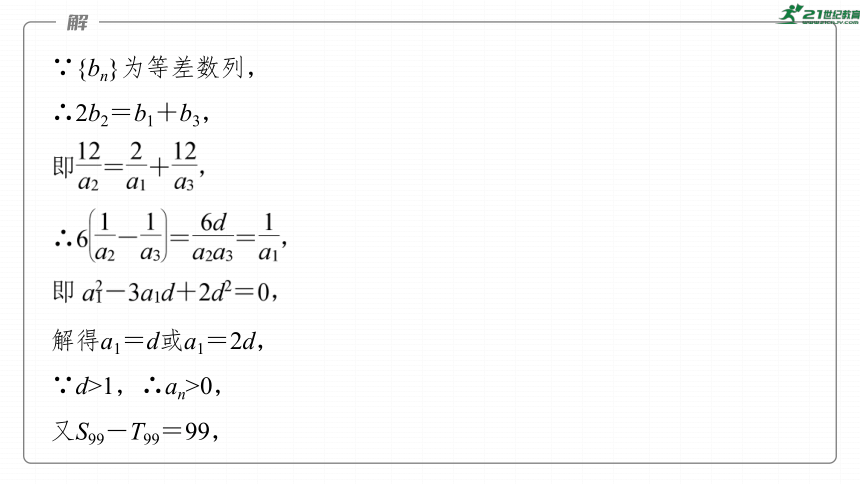


文档简介
(共58张PPT)
专题三 数 列
微专题21
等差数列、等比数列
高考必考内容,主要考查等差数列与等比数列的通项公式与前n项和公式以及性质的应用,等差数列、等比数列的判断与证明,常以选择题、填空题或综合解答题的形式考查,属于中档题目.
考情分析
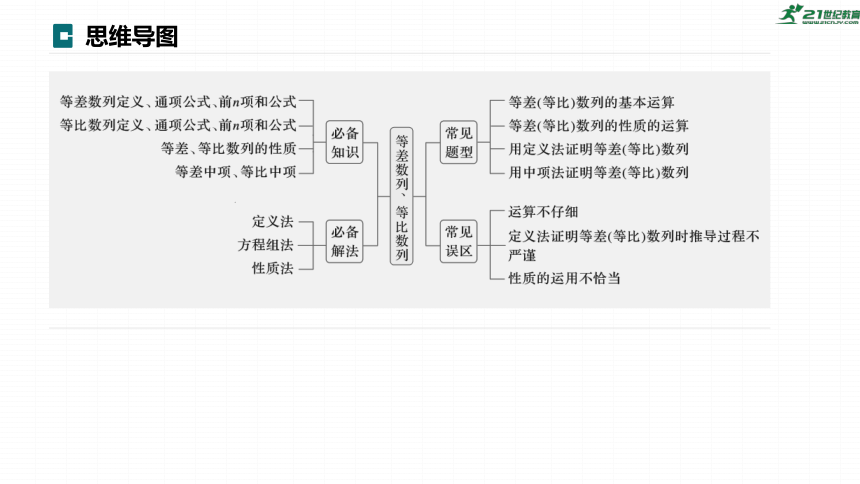
思维导图
内容索引
典型例题
热点突破
考点一 等差、等比数列的基本运算
典例1 (1)(2023·全国乙卷)已知{an}为等比数列,a2a4a5=a3a6,a9a10=
-8,则a7=________.
-2
设{an}的公比为q(q≠0),
则a2a4a5=a3a6=a2q·a5q,
显然an≠0,
则a4=q2,即a1q3=q2,
则a1q=1,
因为a9a10=-8,
则a1q8·a1q9=-8,
则q15=(q5)3=-8=(-2)3,
则q5=-2,则a7=a1q·q5=q5=-2.
∵3a2=3a1+a3,
∴3d=a1+2d,解得a1=d,
∴S3=3a2=3(a1+d)=6d,
an=a1+(n-1)d=nd,
即2d2-7d+3=0,
∴an=nd=3n.
②若{bn}为等差数列,且S99-T99=99,求d.
∵{bn}为等差数列,
∴2b2=b1+b3,
解得a1=d或a1=2d,
∵d>1,∴an>0,
又S99-T99=99,
由等差数列的性质知,
99a50-99b50=99,
即a50-b50=1,
解得a50=51或a50=-50(舍去).
当a1=2d时,a50=a1+49d=51d=51,
解得d=1,与d>1矛盾,无解;
当a1=d时,a50=a1+49d=50d=51,
跟踪训练1 (1)(2023·全国甲卷)记Sn为等比数列{an}的前n项和.若8S6=
7S3,则{an}的公比为________.
若q=1,
则由8S6=7S3得8·6a1=7·3a1,
则a1=0,不符合题意.
所以q≠1.
当q≠1时,因为8S6=7S3,
即8(1-q6)=7(1-q3),
即8(1+q3)(1-q3)=7(1-q3),
538
设等差数列{an}的公差为d,等比数列{bn}的公比为q,且q>0,
因为b5=b=16,则b1q4=(b1q)4=16,可得q=2,b1=1,
因为cn=an+bn,
所以T9=c1+c2+…+c9=(a1+a2+…+a9)+(b1+b2+…+b9)
典例2 (1)已知等差数列{an}的前n项和为Sn,若a1=2,且S3=S19,则S21等于
A.2 B.3 C.4 D.6
考点二 等差、等比数列的性质
√
因为S3=S19,
所以a1+a2+a3=a1+a2+a3+a4+a5+…+a19,
所以a4+a5+…+a19=8(a4+a19)=0,
即a4+a19=0,
S21=a1+a2+a3+a4+a5+…+a19+a20+a21
=a1+a2+a3+a20+a21
=a1+2(a4+a19)=a1=2.
(2)(2023·新高考全国Ⅱ)记Sn为等比数列{an}的前n项和,若S4=-5,S6=21S2,则S8等于
A.120 B.85 C.-85 D.-120
√
方法一 设等比数列{an}的公比为q,首项为a1,
若q=1,则S6=6a1=3×2a1=3S2,不符合题意,
所以q≠1.
由S4=-5,S6=21S2,
由①可得,1+q2+q4=21,解得q2=4,
方法二 设等比数列{an}的公比为q,
因为S4=-5,S6=21S2,
所以q≠-1,否则S4=0,
从而S2,S4-S2,S6-S4,S8-S6成等比数列,
所以(-5-S2)2=S2(21S2+5),
当S2=-1时,S2,S4-S2,S6-S4,S8-S6,
即为-1,-4,-16,S8+21,
易知S8+21=-64,即S8=-85;
S4=a1+a2+a3+a4=(a1+a2)(1+q2)=(1+q2)S2>0,
与S4=-5矛盾,舍去.
综上,S8=-85.
跟踪训练2
√
由题意得an>0,
∵正项等比数列{an}满足a10=1,根据等比数列的性质得a1·a19=a2·a18=…=a9·a11=1,
根据f(x)+f(-x)=1得
考点三 等差、等比数列的判断与证明
典例3 已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-bn+4,4bn+1=3bn-an-4.
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列;
由题设得4(an+1+bn+1)=2(an+bn),
由题设得4(an+1-bn+1)=4(an-bn)+8,即an+1-bn+1=an-bn+2.
又因为a1-b1=1,所以{an-bn}是首项为1,公差为2的等差数列.
(2)求{an}和{bn}的通项公式.
跟踪训练3 (2022·全国甲卷)记Sn为数列{an}的前n项和.已知 +n=2an+1.
(1)证明:{an}是等差数列;
得2Sn+n2=2an·n+n, ①
所以2Sn+1+(n+1)2=2an+1·(n+1)+(n+1), ②
②-①,得
2an+1+2n+1=2an+1·(n+1)-2an·n+1,
化简得an+1-an=1,
所以数列{an}是公差为1的等差数列.
(2)若a4,a7,a9成等比数列,求Sn的最小值.
由(1)知数列{an}的公差为1.
由a4,a7,a9成等比数列,得a=a4a9,即
(a1+6)2=(a1+3)(a1+8),
解得a1=-12.
所以当n=12或13时,Sn取得最小值,最小值为-78.
总结提升
1.证明数列{an}是等差数列的两种基本方法
(1)利用定义,证明an+1-an(n∈N*)为常数;
(2)利用等差中项,即证明2an=an-1+an+1(n≥2,n∈N*).
2.证明数列{an}是等比数列的两种基本方法
1
2
3
4
5
6
7
8
9
10
1.(2023·聊城模拟)已知等差数列{an}的前n项和为Sn,且a5=5,a1+S11=67,则a3a10是{an}中的
A.第30项 B.第36项
C.第48项 D.第60项
√
1
2
3
4
5
6
7
8
9
10
设等差数列{an}的公差为d,由a5=5,得a1+4d=5; ①
由①②解得a1=1,d=1,所以an=n,
于是a3a10=3×10=30,而a30=30,故a3a10是{an}中的第30项.
1
2
3
4
5
6
7
8
9
10
2.(2023·武汉模拟)已知等比数列{an}满足a6=2,且a7,a5,a9成等差数列,则a4等于
A.-2 B.-1 C.1 D.2
√
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
方法一 设等比数列{an}的公比为q,
由a5-a3=a1q4-a1q2=12a1=12,得a1=1.
1
2
3
4
5
6
7
8
9
10
方法二 设等比数列{an}的公比为q,
将q=2代入①,解得a3=4.
1
2
3
4
5
6
7
8
9
10
4.(2023·南京模拟)已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,如图所示,在宝塔形数表中位于第i行,第j列的数记为ai,j,比如a3,2=9,a4,2=15,a5,4=23,若ai,j=2 017,则i+j等于
A.64 B.65 C.71 D.72
√
1
2
3
4
5
6
7
8
9
10
数列1,3,5,…是首项为1,公差为2的等差数列,
记其通项公式为bn=2n-1,
令bn1=2n1-1=2 017,解得n1=1 009.
宝塔形数自上而下,每行的项数是1,2,3,…,
即首项是1,公差是1的等差数列,
记其通项公式为cn=n,
所以n1=1 009是第45行的数,即i=45.
1
2
3
4
5
6
7
8
9
10
第45行是奇数行,是从右边开始向左边递增,
即从b991=2×991-1=1 981,
即{bn}的第991项,递增到第1 009项,也即从右往左第19项.
故从左往右是第45-19+1=27项,所以j=27.所以i+j=45+27=72.
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·湛江模拟)一百零八塔始建于西夏时期,是中国现存最大且排列最整齐的塔群之一,塔群随山势凿石分阶而建,自上而下一共12层,第1层有1座塔,从第2层开始每层的塔数均不少于上一层的塔数,总计108座塔.已知包括第1层在内的其中10层的塔数可以构成等差数列{an},剩下2层的塔数分别与上一层的塔数相等,第1层与第2层的塔数不同,则
A.第3层的塔数为3
B.第6层的塔数为9
C.第4层与第5层的塔数相等
D.等差数列{an}的公差为2
√
√
√
1
2
3
4
5
6
7
8
9
10
设等差数列{an}的公差为d,
则最多有55+10+10=75(座)塔,不符合题意;
塔数依次是1,3,5,7,9,11,13,15,17,19,依题意知剩下2层的塔数为3与5,所以这12层塔的塔数分别为1,3,3,5,5,7,9,11,13,15,17,19,因此A,C,D正确,B错误.
1
2
3
4
5
6
7
8
9
10
6.(多选)(2023·常德模拟)数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词源于希腊文,它的原意是“旋卷”或“缠卷”.小明对螺旋线有着浓厚的兴趣,连接嵌套的各个正方形的顶点就得到了近似于螺旋线的美丽图案,其具体作法是:在边长为1的正方形ABCD中,作它的内接正方形EFGH,且使得∠BEF=15°;再作正方形EFGH的内接正方形MNPQ,且使得∠FMN=15°;与之类似,依次进行,就形成了阴影部分的
图案,如图所示.设第n个正方形的边长为an(其中第1个正方形ABCD的边长为a1=AB,第2个正方形EFGH的边长为a2=EF,…),第n个直角三角形(阴影部分)的面积为Sn(其中第1个直角三角形AEH的面积为S1,第2个直角三角形EQM的面积为S2,…),则
1
2
3
4
5
6
7
8
9
10
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
4
1
2
3
4
5
6
7
8
9
10
设等差数列{an}的公差为d,由a2=3a1,
得a1+d=3a1,即d=2a1,
1
2
3
4
5
6
7
8
9
10
23
16.9
1
2
3
4
5
6
7
8
9
10
16.9
1
2
3
4
5
6
7
8
9
10
而a1=2满足上式,因此an=
由an=am-n得
即n2-23n+20=(m-n)2-23(m-n)+20,
整理得m(2n-m)=23(2n-m),又n为小于m的任意正整数,所以m=23.
1
2
3
4
5
6
7
8
9
10
将n=1代入得,a2=4a1=4.
将n=2代入得,a3=3a2=12.
所以b1=1,b2=2,b3=4.
1
2
3
4
5
6
7
8
9
10
(2)判断数列{bn}是不是等比数列,并说明理由;
{bn}是首项为1,公比为2的等比数列.理由如下:
又b1=1,所以{bn}是首项为1,公比为2的等比数列.
1
2
3
4
5
6
7
8
9
10
(3)求{an}的通项公式.
所以an=n·2n-1(n∈N*).
1
2
3
4
5
6
7
8
9
10
10.(2022·新高考全国Ⅱ)已知{an}是等差数列,{bn}是公比为2的等比数列,且a2-b2=a3-b3=b4-a4.
(1)证明:a1=b1;
设等差数列{an}的公差为d,
由a2-b2=a3-b3,得a1+d-2b1=a1+2d-4b1,即d=2b1,
由a2-b2=b4-a4,得a1+d-2b1=8b1-(a1+3d),即a1=5b1-2d,
将d=2b1代入,得a1=5b1-2×2b1=b1,
即a1=b1.
1
2
3
4
5
6
7
8
9
10
(2)求集合{k|bk=am+a1,1≤m≤500}中元素的个数.
由(1)知,an=a1+(n-1)d=a1+(n-1)×2b1=(2n-1)a1,bn=b1·2n-1,
由bk=am+a1,得b1·2k-1=(2m-1)a1+a1,
由a1=b1≠0得2k-1=2m,
由题知1≤m≤500,所以2≤2m≤1 000,所以k=2,3,4,…,10,共9个数,即集合{k|bk=am+a1,1≤m≤500}={2,3,4,…,10}中元素的个数为9.
专题三 数 列
微专题21
等差数列、等比数列
高考必考内容,主要考查等差数列与等比数列的通项公式与前n项和公式以及性质的应用,等差数列、等比数列的判断与证明,常以选择题、填空题或综合解答题的形式考查,属于中档题目.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 等差、等比数列的基本运算
典例1 (1)(2023·全国乙卷)已知{an}为等比数列,a2a4a5=a3a6,a9a10=
-8,则a7=________.
-2
设{an}的公比为q(q≠0),
则a2a4a5=a3a6=a2q·a5q,
显然an≠0,
则a4=q2,即a1q3=q2,
则a1q=1,
因为a9a10=-8,
则a1q8·a1q9=-8,
则q15=(q5)3=-8=(-2)3,
则q5=-2,则a7=a1q·q5=q5=-2.
∵3a2=3a1+a3,
∴3d=a1+2d,解得a1=d,
∴S3=3a2=3(a1+d)=6d,
an=a1+(n-1)d=nd,
即2d2-7d+3=0,
∴an=nd=3n.
②若{bn}为等差数列,且S99-T99=99,求d.
∵{bn}为等差数列,
∴2b2=b1+b3,
解得a1=d或a1=2d,
∵d>1,∴an>0,
又S99-T99=99,
由等差数列的性质知,
99a50-99b50=99,
即a50-b50=1,
解得a50=51或a50=-50(舍去).
当a1=2d时,a50=a1+49d=51d=51,
解得d=1,与d>1矛盾,无解;
当a1=d时,a50=a1+49d=50d=51,
跟踪训练1 (1)(2023·全国甲卷)记Sn为等比数列{an}的前n项和.若8S6=
7S3,则{an}的公比为________.
若q=1,
则由8S6=7S3得8·6a1=7·3a1,
则a1=0,不符合题意.
所以q≠1.
当q≠1时,因为8S6=7S3,
即8(1-q6)=7(1-q3),
即8(1+q3)(1-q3)=7(1-q3),
538
设等差数列{an}的公差为d,等比数列{bn}的公比为q,且q>0,
因为b5=b=16,则b1q4=(b1q)4=16,可得q=2,b1=1,
因为cn=an+bn,
所以T9=c1+c2+…+c9=(a1+a2+…+a9)+(b1+b2+…+b9)
典例2 (1)已知等差数列{an}的前n项和为Sn,若a1=2,且S3=S19,则S21等于
A.2 B.3 C.4 D.6
考点二 等差、等比数列的性质
√
因为S3=S19,
所以a1+a2+a3=a1+a2+a3+a4+a5+…+a19,
所以a4+a5+…+a19=8(a4+a19)=0,
即a4+a19=0,
S21=a1+a2+a3+a4+a5+…+a19+a20+a21
=a1+a2+a3+a20+a21
=a1+2(a4+a19)=a1=2.
(2)(2023·新高考全国Ⅱ)记Sn为等比数列{an}的前n项和,若S4=-5,S6=21S2,则S8等于
A.120 B.85 C.-85 D.-120
√
方法一 设等比数列{an}的公比为q,首项为a1,
若q=1,则S6=6a1=3×2a1=3S2,不符合题意,
所以q≠1.
由S4=-5,S6=21S2,
由①可得,1+q2+q4=21,解得q2=4,
方法二 设等比数列{an}的公比为q,
因为S4=-5,S6=21S2,
所以q≠-1,否则S4=0,
从而S2,S4-S2,S6-S4,S8-S6成等比数列,
所以(-5-S2)2=S2(21S2+5),
当S2=-1时,S2,S4-S2,S6-S4,S8-S6,
即为-1,-4,-16,S8+21,
易知S8+21=-64,即S8=-85;
S4=a1+a2+a3+a4=(a1+a2)(1+q2)=(1+q2)S2>0,
与S4=-5矛盾,舍去.
综上,S8=-85.
跟踪训练2
√
由题意得an>0,
∵正项等比数列{an}满足a10=1,根据等比数列的性质得a1·a19=a2·a18=…=a9·a11=1,
根据f(x)+f(-x)=1得
考点三 等差、等比数列的判断与证明
典例3 已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-bn+4,4bn+1=3bn-an-4.
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列;
由题设得4(an+1+bn+1)=2(an+bn),
由题设得4(an+1-bn+1)=4(an-bn)+8,即an+1-bn+1=an-bn+2.
又因为a1-b1=1,所以{an-bn}是首项为1,公差为2的等差数列.
(2)求{an}和{bn}的通项公式.
跟踪训练3 (2022·全国甲卷)记Sn为数列{an}的前n项和.已知 +n=2an+1.
(1)证明:{an}是等差数列;
得2Sn+n2=2an·n+n, ①
所以2Sn+1+(n+1)2=2an+1·(n+1)+(n+1), ②
②-①,得
2an+1+2n+1=2an+1·(n+1)-2an·n+1,
化简得an+1-an=1,
所以数列{an}是公差为1的等差数列.
(2)若a4,a7,a9成等比数列,求Sn的最小值.
由(1)知数列{an}的公差为1.
由a4,a7,a9成等比数列,得a=a4a9,即
(a1+6)2=(a1+3)(a1+8),
解得a1=-12.
所以当n=12或13时,Sn取得最小值,最小值为-78.
总结提升
1.证明数列{an}是等差数列的两种基本方法
(1)利用定义,证明an+1-an(n∈N*)为常数;
(2)利用等差中项,即证明2an=an-1+an+1(n≥2,n∈N*).
2.证明数列{an}是等比数列的两种基本方法
1
2
3
4
5
6
7
8
9
10
1.(2023·聊城模拟)已知等差数列{an}的前n项和为Sn,且a5=5,a1+S11=67,则a3a10是{an}中的
A.第30项 B.第36项
C.第48项 D.第60项
√
1
2
3
4
5
6
7
8
9
10
设等差数列{an}的公差为d,由a5=5,得a1+4d=5; ①
由①②解得a1=1,d=1,所以an=n,
于是a3a10=3×10=30,而a30=30,故a3a10是{an}中的第30项.
1
2
3
4
5
6
7
8
9
10
2.(2023·武汉模拟)已知等比数列{an}满足a6=2,且a7,a5,a9成等差数列,则a4等于
A.-2 B.-1 C.1 D.2
√
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
方法一 设等比数列{an}的公比为q,
由a5-a3=a1q4-a1q2=12a1=12,得a1=1.
1
2
3
4
5
6
7
8
9
10
方法二 设等比数列{an}的公比为q,
将q=2代入①,解得a3=4.
1
2
3
4
5
6
7
8
9
10
4.(2023·南京模拟)已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,如图所示,在宝塔形数表中位于第i行,第j列的数记为ai,j,比如a3,2=9,a4,2=15,a5,4=23,若ai,j=2 017,则i+j等于
A.64 B.65 C.71 D.72
√
1
2
3
4
5
6
7
8
9
10
数列1,3,5,…是首项为1,公差为2的等差数列,
记其通项公式为bn=2n-1,
令bn1=2n1-1=2 017,解得n1=1 009.
宝塔形数自上而下,每行的项数是1,2,3,…,
即首项是1,公差是1的等差数列,
记其通项公式为cn=n,
所以n1=1 009是第45行的数,即i=45.
1
2
3
4
5
6
7
8
9
10
第45行是奇数行,是从右边开始向左边递增,
即从b991=2×991-1=1 981,
即{bn}的第991项,递增到第1 009项,也即从右往左第19项.
故从左往右是第45-19+1=27项,所以j=27.所以i+j=45+27=72.
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·湛江模拟)一百零八塔始建于西夏时期,是中国现存最大且排列最整齐的塔群之一,塔群随山势凿石分阶而建,自上而下一共12层,第1层有1座塔,从第2层开始每层的塔数均不少于上一层的塔数,总计108座塔.已知包括第1层在内的其中10层的塔数可以构成等差数列{an},剩下2层的塔数分别与上一层的塔数相等,第1层与第2层的塔数不同,则
A.第3层的塔数为3
B.第6层的塔数为9
C.第4层与第5层的塔数相等
D.等差数列{an}的公差为2
√
√
√
1
2
3
4
5
6
7
8
9
10
设等差数列{an}的公差为d,
则最多有55+10+10=75(座)塔,不符合题意;
塔数依次是1,3,5,7,9,11,13,15,17,19,依题意知剩下2层的塔数为3与5,所以这12层塔的塔数分别为1,3,3,5,5,7,9,11,13,15,17,19,因此A,C,D正确,B错误.
1
2
3
4
5
6
7
8
9
10
6.(多选)(2023·常德模拟)数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词源于希腊文,它的原意是“旋卷”或“缠卷”.小明对螺旋线有着浓厚的兴趣,连接嵌套的各个正方形的顶点就得到了近似于螺旋线的美丽图案,其具体作法是:在边长为1的正方形ABCD中,作它的内接正方形EFGH,且使得∠BEF=15°;再作正方形EFGH的内接正方形MNPQ,且使得∠FMN=15°;与之类似,依次进行,就形成了阴影部分的
图案,如图所示.设第n个正方形的边长为an(其中第1个正方形ABCD的边长为a1=AB,第2个正方形EFGH的边长为a2=EF,…),第n个直角三角形(阴影部分)的面积为Sn(其中第1个直角三角形AEH的面积为S1,第2个直角三角形EQM的面积为S2,…),则
1
2
3
4
5
6
7
8
9
10
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
4
1
2
3
4
5
6
7
8
9
10
设等差数列{an}的公差为d,由a2=3a1,
得a1+d=3a1,即d=2a1,
1
2
3
4
5
6
7
8
9
10
23
16.9
1
2
3
4
5
6
7
8
9
10
16.9
1
2
3
4
5
6
7
8
9
10
而a1=2满足上式,因此an=
由an=am-n得
即n2-23n+20=(m-n)2-23(m-n)+20,
整理得m(2n-m)=23(2n-m),又n为小于m的任意正整数,所以m=23.
1
2
3
4
5
6
7
8
9
10
将n=1代入得,a2=4a1=4.
将n=2代入得,a3=3a2=12.
所以b1=1,b2=2,b3=4.
1
2
3
4
5
6
7
8
9
10
(2)判断数列{bn}是不是等比数列,并说明理由;
{bn}是首项为1,公比为2的等比数列.理由如下:
又b1=1,所以{bn}是首项为1,公比为2的等比数列.
1
2
3
4
5
6
7
8
9
10
(3)求{an}的通项公式.
所以an=n·2n-1(n∈N*).
1
2
3
4
5
6
7
8
9
10
10.(2022·新高考全国Ⅱ)已知{an}是等差数列,{bn}是公比为2的等比数列,且a2-b2=a3-b3=b4-a4.
(1)证明:a1=b1;
设等差数列{an}的公差为d,
由a2-b2=a3-b3,得a1+d-2b1=a1+2d-4b1,即d=2b1,
由a2-b2=b4-a4,得a1+d-2b1=8b1-(a1+3d),即a1=5b1-2d,
将d=2b1代入,得a1=5b1-2×2b1=b1,
即a1=b1.
1
2
3
4
5
6
7
8
9
10
(2)求集合{k|bk=am+a1,1≤m≤500}中元素的个数.
由(1)知,an=a1+(n-1)d=a1+(n-1)×2b1=(2n-1)a1,bn=b1·2n-1,
由bk=am+a1,得b1·2k-1=(2m-1)a1+a1,
由a1=b1≠0得2k-1=2m,
由题知1≤m≤500,所以2≤2m≤1 000,所以k=2,3,4,…,10,共9个数,即集合{k|bk=am+a1,1≤m≤500}={2,3,4,…,10}中元素的个数为9.
同课章节目录
