高考数学专题四立体几何 微专题25 空间几何体 课件(共75张PPT)
文档属性
| 名称 | 高考数学专题四立体几何 微专题25 空间几何体 课件(共75张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览










文档简介
(共75张PPT)
专题四 立体几何
微专题25
空间几何体
空间几何体的结构特征是立体几何的基础,空间几何体的表面积和体积是高考的重点与热点,多以选择题、填空题的形式考查,难度中等或偏上.
考情分析
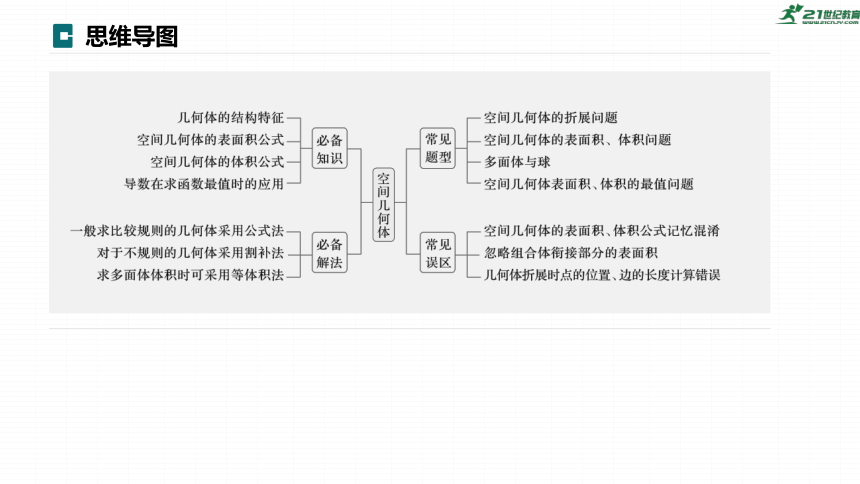
思维导图
内容索引
典型例题
热点突破
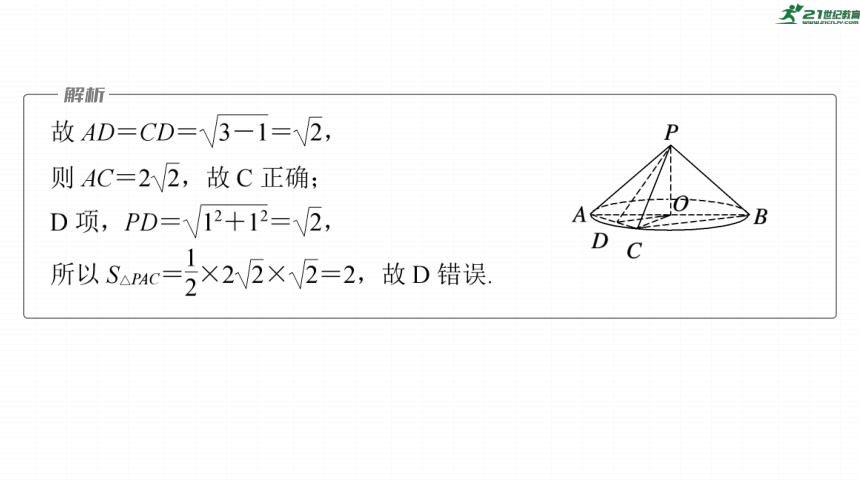
典例1 (1)(多选)(2023·新高考全国Ⅱ)已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,PA=2,点C在底面圆周上,且二面角P-AC-O为45°,则
√
考点一 表面积与体积
√
依题意,∠APB=120°,PA=2,
C项,取AC的中点D,连接OD,PD,如图所示,
则AC⊥OD,AC⊥PD,所以∠PDO是二面角
P-AC-O的平面角,
则∠PDO=45°,所以OP=OD=1,
(2)(2023·新高考全国Ⅰ)在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=
1,AA1= 则该棱台的体积为_____.
如图,过A1作A1M⊥AC,垂足为M,
易知A1M为四棱台ABCD-A1B1C1D1的高,
跟踪训练1 (1)(2023·广州模拟)已知一个圆锥和圆柱的底面半径和高分别相等,若圆锥的轴截面是等边三角形,则这个圆锥和圆柱的侧面积之比为
√
设圆锥和圆柱的底面半径为r,
因为圆锥的轴截面是等边三角形,所以圆锥的母线长l=2r,
所以圆锥的侧面积S1=πrl=2πr2,
(2)(多选)(2022·新高考全国Ⅱ)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB.记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则
A.V3=2V2
B.V3=V1
C.V3=V1+V2
D.2V3=3V1
√
√
如图,连接BD交AC于O,连接OE,OF.
设AB=ED=2FB=2,
则AB=BC=CD=AD=2,FB=1.
因为ED⊥平面ABCD,FB∥ED,
所以FB⊥平面ABCD,
因为ED⊥平面ABCD,AC 平面ABCD,
所以ED⊥AC,
又AC⊥BD,
且ED∩BD=D,ED,BD 平面BDEF,
所以AC⊥平面BDEF.
因为OE,OF 平面BDEF,
所以AC⊥OE,AC⊥OF.
所以EF2=OE2+OF2,所以OF⊥OE.
又OE∩AC=O,OE,AC 平面ACE,
所以OF⊥平面ACE,
所以V3≠2V2,V1≠V3,V3=V1+V2,2V3=3V1,
所以选项A,B不正确,选项C,D正确.
典例2 (1)“莫言下岭便无难,赚得行人空喜欢.”出自南宋诗人杨万里的作品《过松源晨炊漆公店》.如图是一座山的示意图,山大致呈圆锥形,山脚呈圆形,半径为40 km,山高为 B是山坡SA上一点,且AB=40 km.为了发展旅游业,要建设一条从A到B的环山观光
公路,这条公路从A出发后先上坡,后下坡,当公路长度
最短时,下坡路段长为
A.60 km B.
C.72 km D.
√
考点二 空间几何体的折展问题
如图为圆锥的侧面展开图,连接A′B,
由两点之间线段最短,知观光公路为图中的A′B,
过点S作A′B的垂线,垂足为H,
记点P为A′B上任意一点,连接PS,当上坡时,P到山顶S的距离PS越来越小,当下坡时,P到山顶S的距离PS越来越大,
则下坡路段为图中的HB,
由Rt△SA′B∽Rt△HSB,
(2)(2023·黄山模拟)如图1,将一块边长为20的正方形纸片ABCD剪去四个全等的等腰△PEE1,△PFF1,△PGG1,△PHH1,再将剩下的部分沿虚线折成一个正四棱锥P-EFGH,使E与E1重合,F与F1重合,G与G1重合,H与H1重合,点A,B,C,D重合于点O,如图2.则正四棱锥P-EFGH体积的最大值为
√
根据题意,PG是侧棱,底面正方形EFGH的对角线的一半是GC,
设GC=x,0底面正方形EFGH的面积S=4S△OFG=2x2,
∴四棱锥P-EFGH的体积
∴当t2=40 时,V取最大值,
跟踪训练2 (1)(2023·广东大湾区联考)如图为三棱锥A-BCD的平面展开图,其中AC=CD=CB=2,AE⊥BD,垂足为C,则该三棱锥的体
积为____.
由三棱锥A-BCD的平面展开图可得其直观图,如图所示.
其中AC⊥CD,AC⊥CB,CD⊥CB,AC=CD=CB=2,
又BC∩CD=C,BC,CD 平面BCD,所以AC⊥平面BCD,
(2)如图所示是一个底面半径和高分别为1和4的圆柱形开口容器(下表面密封),P是母线BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一米粒,若这只蚂蚁要先爬到上口边缘再爬到点P处取得米粒,则它所需经过的最短路程为
√
依题意可得圆柱的底面半径r=1,高h=4,
将圆柱的侧面(一半)展开后得矩形ABCD,其中AB=π,
AD=4,
问题转化为在CD上找一点Q,使AQ+PQ最短,
作P关于CD的对称点E,连接AE,AE与CD交于点Q,
则得AQ+PQ的最小值就是
典例3 (1)(2022·新高考全国Ⅰ)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为36π,且3≤l≤ 则该正四棱锥体积的
取值范围是
考点三 多面体与球
√
方法一 如图,设该球的球心为O,半径为R,正四棱锥的底面边长为a,高为h,
依题意,得36π=
解得R=3.
方法二 如图,设该球的球心为O,半径为R,正四棱锥的底面边长为a,高为h,
依题意,得36π=
解得R=3.
方法三 如图,设该球的半径为R,球心为O,正四棱锥的底面边长为a,高为h,正四棱锥的侧棱与高所成的角为θ,
依题意,得36π=
解得R=3,
所以正四棱锥的底面边长a=
高h=lcos θ.
在△OPC中,作OE⊥PC,垂足为E,
所以l=6cos θ,
所以正四棱锥的体积
则y=sin θcos2θ=t(1-t2)=t-t3,
(2)(2023·南昌模拟)如图,在正四棱锥P-ABCD框架内放一个球O,球O与侧棱PA,PB,PC,PD均相切.若∠APB= 且OP=2,则球O的表面积为_____.
8π
在正四棱锥P-ABCD中,∠APB=
则△PAB是正三角形,
于是AC2=AB2+BC2=PA2+PC2,所以∠APC=
因为球O与侧棱PA,PB,PC,PD均相切,
则由对称性知,平面PAC截正四棱锥得等腰直角三角形,
截球O得球O的大圆,且圆O与直角边PA,PC都相切,如图,
显然OP平分∠APC,因此球O的半径R=
所以球O的表面积为4πR2=8π.
跟踪训练3 (1)(2022·全国乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为
√
该四棱锥的体积最大即以底面截球的圆面和顶点O组成的圆锥体积最大.
设圆锥的高为h(0√
如图所示,
因为CC1⊥AC,AA1⊥BC CC1⊥BC,AC∩BC=C,AC,BC 平面ABC,
所以CC1⊥平面ABC,
又因为平面A1BC⊥平面AA1B,
平面A1BC∩平面AA1B=A1B,
过点A作AE⊥A1B,
则AE⊥平面A1BC,
则AE⊥BC,
又因为AA1⊥BC,AA1∩AE=A,AA1,AE 平面ABB1A1,
所以BC⊥平面ABB1A1,
又AB 平面ABB1A1,
所以AB⊥BC.
设AB=c,AC=b,BC=a,
则b2=a2+c2,
又因为三棱柱内切球的体积为
设内切球的半径为R,
解得ac=12,因为棱柱的高等于内切球直径2,
故三棱锥A-A1BC的体积为4.
空间几何体在高考题中主要考查表面积、体积问题,常见题型求解思路有两种,一是对于规则的几何体直接使用公式法求解,二是将不规则的几何体分解成基本的柱、锥、台体,先求这些柱、锥、台体的表面积或体积,再通过求和或作差得不规则几何体的表面积或体积.
提醒:组合体的表面积问题注意衔接部分的处理.旋转体的表面积问题注意其侧面展开图的应用.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
1.(2023·深圳模拟)圆锥侧面展开图扇形的圆心角为60°,底面圆的半径为8,则圆锥的侧面积为
A.384π B.392π C.398π D.404π
√
设圆锥的半径为r,母线长为l,则r=8,
由题意知,2πr=
解得l=48,
所以圆锥的侧面积为πrl=8×48π=384π.
1
2
3
4
5
6
7
8
9
10
11
12
2.(2023·惠州模拟)如图1,在高为h的直三棱柱容器ABC-A1B1C1中,AB=AC=2,AB⊥AC.现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为△A1B1C(如图2),则容器的高h为
A. B.3 C.4 D.6
√
1
2
3
4
5
6
7
8
9
10
11
12
由图2知 ,
其中h表示三棱柱的高,
故
,
因此,无水部分体积与有水部分体积之比为1∶2,所以图1中高度之比为1∶2,则h=3.
1
2
3
4
5
6
7
8
9
10
11
12
3.(2023·日照模拟)红灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼,营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上、下两部分是两个相同的圆柱的侧面,中间是球面除去上、下两个相同球冠剩下的部分.如图2,球冠是由球面被平面截得的一部分,垂直于截面的直径被截得的部分叫做球冠的高,若球冠所在球面的半径为R,球冠的高为h,则球冠的面积S=2πRh.如图1,已知该灯笼的高为58 cm,圆柱的高为5 cm,圆柱的底面圆直径为
14 cm,则围成该灯笼中间球面部分所
需布料的面积为
A.1 940π cm2 B.2 350π cm2
C.2 400π cm2 D.2 540π cm2
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
所以两个球冠的面积为2S=2×2πRh
=2×2×π×25×1=100π(cm2),
则围成该灯笼中间球面部分所需布料
的面积为4πR2-2S=4×π×252-100π=2 400π(cm2).
1
2
3
4
5
6
7
8
9
10
11
12
4.(2023·娄底模拟) 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=CA=AA1,点D是棱AA1上的点,AD= AA1,若截面BDC1分这个棱柱为两部分,则这两部分的体积比为
A.1∶2 B.4∶5
C.4∶9 D.5∶7
√
1
2
3
4
5
6
7
8
9
10
11
12
不妨令AB=BC=CA=AA1=4,且上、下底面为等边三角形,
又AA1⊥底面ABC,易知三棱柱ABC-A1B1C1为直三棱柱,所以侧面为正方形,
所以三棱柱ABC-A1B1C1的体积V=AA1·S△ABC=
而AD=1,CC1=4,故 = AC·(AD+CC1)=10,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
5.(2023·佛山模拟)科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,极目一号(如图1)是中国科学院空天信息研究院自主研发的系留浮空器.截至2022年5月,“极目一号”Ⅲ型浮空艇成功完成10次升空大气科学观测,最高升空至9 050 m,超过珠穆朗玛峰,创造了浮空艇原位大气科学观测海拔最高的世界纪录,彰显了中国的实力.“极目一号”Ⅲ型浮空艇长55 m,高19 m,若将它近似看作一个半球、一个圆柱和一个圆台的组合体,正视图如图2所示,则“极目一号”Ⅲ型浮空艇的体积约为(参考数据:9.52≈90,9.53≈857,315×1 005≈
316 600,π≈3.14)
A.9 064 m3 B.9 004 m3
C.8 944 m3 D.8 884 m3
√
1
2
3
4
5
6
7
8
9
10
11
12
V圆柱=π×9.52×14≈1 260π(m3),
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
由题可知矩形ABCD所在截面圆的半径r即为矩形ABCD的对角线长度的一半,
√
√
1
2
3
4
5
6
7
8
9
10
11
12
7.(多选)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台O1O2,在轴截面ABCD中,AB=AD=BC=2 cm,且CD=2AB,则
A.该圆台的高为1 cm
D.一只小虫从点C沿着该圆台的侧面爬行到AD的中点,所经过的最短路
程为5 cm
√
1
2
3
4
5
6
7
8
9
10
11
12
由圆台补成圆锥,可得大圆锥的母线长为4 cm,底面半径为2 cm,侧
面展开图的圆心角θ= =π,
1
2
3
4
5
6
7
8
9
10
11
12
设P为AD的中点,连接CP,如图2,可得∠COD= OC=4 cm,OP=3 cm,
则CP= =5(cm),从点C沿着该圆台的侧面爬行到AD的中点,所经过的最短路程为5 cm,故D正确.
8.(多选)(2023·新高考全国Ⅰ)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有
A.直径为0.99 m的球体
B.所有棱长均为1.4 m的四面体
C.底面直径为0.01 m,高为1.8 m的圆柱体
D.底面直径为1.2 m,高为0.01 m的圆柱体
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
对于A,因为0.99 m<1 m,即球体的直径小于正方体的棱长,
所以能够被整体放入正方体内,故A正确;
1
2
3
4
5
6
7
8
9
10
11
12
所以能够被整体放入正方体内,故B正确;
所以不能够被整体放入正方体内,故C错误;
对于D,
因为1.2 m>1 m,可知底面正方形不能包含圆
柱的底面圆,如图,
过AC1的中点O作OE⊥AC1,
设OE∩AC=E,
1
2
3
4
5
6
7
8
9
10
11
12
所以以AC1为轴可能对称放置底面直径为1.2 m的圆柱,
若底面直径为1.2 m的圆柱与正方体的上下底面均相切,
设圆柱的底面圆心为O1,与正方体下底面的切点为M,
可知AC1⊥O1M,O1M=0.6,
1
2
3
4
5
6
7
8
9
10
11
12
根据对称性可知圆柱的高为
所以能够被整体放入正方体内,所以D正确.
9.(2023·辽阳模拟)将3个6 cm×6 cm的正方形都沿其中的一对邻边的中点剪开,每个正方形均分成两个部分,如图(1)所示,将这6个部分接入一个边长为 的正六边形上,如图(2)所示.若该平面图沿着正六边形
的边折起,围成一个七面体,则该七面体的体积为_____ cm3.
108
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
将平面图形折叠并补形得到如图所示的正方体,
该七面体为正方体沿着图中的六边形截面截去一部分后剩下的另一部分,由对称性知其体积为正方体体积的一半,即 ×63=108(cm3).
10.棱长为2的正方体ABCD-A1B1C1D1中,M,N分别为棱BB1,AB的中点,则三棱锥A1-D1MN的体积为____.
1
1
2
3
4
5
6
7
8
9
10
11
12
如图,由正方体棱长为2,
1
2
3
4
5
6
7
8
9
10
11
12
又易知D1A1为三棱锥D1-A1MN的高,且D1A1=2,
∴
11.如图,在多面体ABCEF中,D为AB的中点,四边形CDFE为矩形,且DF⊥AB,AC=BC=2,∠ACB=120°,当AE⊥BE时,多面体ABCEF
的体积为_____.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
在△ABC中,因为AC=BC且D为AB的中点,所以CD⊥AB,
又因为DF⊥AB,且DF∩CD=D,DF,CD 平面CDFE,所以AB⊥平面CDFE,
在△ABC中,因为AC=BC=2且∠ACB=120°,CD⊥AB,
因为四边形CDFE为矩形,可得DF⊥CD,
又因为DF⊥AB,AB∩CD=D,AB,CD 平面ABC,所以DF⊥平面ABC,
1
2
3
4
5
6
7
8
9
10
11
12
因为CE∥DF,所以CE⊥平面ABC,
又因为AC,BC 平面ABC,所以CE⊥AC,CE⊥BC,
设CE=m,在Rt△ACE中,可得AE2=AC2+m2=4+m2,
在Rt△BCE中,可得BE2=BC2+m2=4+m2,
因为AE⊥BE,所以AB2=AE2+BE2,即12=4+m2+4+m2,解得m=
所以多面体ABCEF的体积
1
2
3
4
5
6
7
8
9
10
11
12
12.(2023·济宁模拟)l,l′为两条直线,α,β为两个平面,满足:l∩l′=O,l与l′的夹角为 α∥β,l⊥α,α与β之间的距离为2.以l为轴将l′旋
转一周,并用α,β截取得到两个同顶点O(点O在平面α与β之间)的圆锥.设
这两个圆锥的体积分别为V1,V2,则V1+V2的最小值为_____.
两个圆锥的轴截面如图所示,O1,O2分别为两圆锥的底面圆的圆心,
设半径分别为r1,r2,
O1O2⊥DE,O1O2⊥BC,
设OO1=h,因为α与β之间的距离为2,所以OO2=2-h,
1
2
3
4
5
6
7
8
9
10
11
12
由圆锥的性质知,OB=OC,OD=OE,
所以△ODE,△OBC为等边三角形,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
所以当h∈(0,1)时,f′(h)<0;
当h∈(1,2)时,f′(h)>0,
所以f(h)在(0,1)上单调递减,在(1,2)单调递增,
专题四 立体几何
微专题25
空间几何体
空间几何体的结构特征是立体几何的基础,空间几何体的表面积和体积是高考的重点与热点,多以选择题、填空题的形式考查,难度中等或偏上.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)(多选)(2023·新高考全国Ⅱ)已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,PA=2,点C在底面圆周上,且二面角P-AC-O为45°,则
√
考点一 表面积与体积
√
依题意,∠APB=120°,PA=2,
C项,取AC的中点D,连接OD,PD,如图所示,
则AC⊥OD,AC⊥PD,所以∠PDO是二面角
P-AC-O的平面角,
则∠PDO=45°,所以OP=OD=1,
(2)(2023·新高考全国Ⅰ)在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=
1,AA1= 则该棱台的体积为_____.
如图,过A1作A1M⊥AC,垂足为M,
易知A1M为四棱台ABCD-A1B1C1D1的高,
跟踪训练1 (1)(2023·广州模拟)已知一个圆锥和圆柱的底面半径和高分别相等,若圆锥的轴截面是等边三角形,则这个圆锥和圆柱的侧面积之比为
√
设圆锥和圆柱的底面半径为r,
因为圆锥的轴截面是等边三角形,所以圆锥的母线长l=2r,
所以圆锥的侧面积S1=πrl=2πr2,
(2)(多选)(2022·新高考全国Ⅱ)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB.记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则
A.V3=2V2
B.V3=V1
C.V3=V1+V2
D.2V3=3V1
√
√
如图,连接BD交AC于O,连接OE,OF.
设AB=ED=2FB=2,
则AB=BC=CD=AD=2,FB=1.
因为ED⊥平面ABCD,FB∥ED,
所以FB⊥平面ABCD,
因为ED⊥平面ABCD,AC 平面ABCD,
所以ED⊥AC,
又AC⊥BD,
且ED∩BD=D,ED,BD 平面BDEF,
所以AC⊥平面BDEF.
因为OE,OF 平面BDEF,
所以AC⊥OE,AC⊥OF.
所以EF2=OE2+OF2,所以OF⊥OE.
又OE∩AC=O,OE,AC 平面ACE,
所以OF⊥平面ACE,
所以V3≠2V2,V1≠V3,V3=V1+V2,2V3=3V1,
所以选项A,B不正确,选项C,D正确.
典例2 (1)“莫言下岭便无难,赚得行人空喜欢.”出自南宋诗人杨万里的作品《过松源晨炊漆公店》.如图是一座山的示意图,山大致呈圆锥形,山脚呈圆形,半径为40 km,山高为 B是山坡SA上一点,且AB=40 km.为了发展旅游业,要建设一条从A到B的环山观光
公路,这条公路从A出发后先上坡,后下坡,当公路长度
最短时,下坡路段长为
A.60 km B.
C.72 km D.
√
考点二 空间几何体的折展问题
如图为圆锥的侧面展开图,连接A′B,
由两点之间线段最短,知观光公路为图中的A′B,
过点S作A′B的垂线,垂足为H,
记点P为A′B上任意一点,连接PS,当上坡时,P到山顶S的距离PS越来越小,当下坡时,P到山顶S的距离PS越来越大,
则下坡路段为图中的HB,
由Rt△SA′B∽Rt△HSB,
(2)(2023·黄山模拟)如图1,将一块边长为20的正方形纸片ABCD剪去四个全等的等腰△PEE1,△PFF1,△PGG1,△PHH1,再将剩下的部分沿虚线折成一个正四棱锥P-EFGH,使E与E1重合,F与F1重合,G与G1重合,H与H1重合,点A,B,C,D重合于点O,如图2.则正四棱锥P-EFGH体积的最大值为
√
根据题意,PG是侧棱,底面正方形EFGH的对角线的一半是GC,
设GC=x,0
∴四棱锥P-EFGH的体积
∴当t2=40 时,V取最大值,
跟踪训练2 (1)(2023·广东大湾区联考)如图为三棱锥A-BCD的平面展开图,其中AC=CD=CB=2,AE⊥BD,垂足为C,则该三棱锥的体
积为____.
由三棱锥A-BCD的平面展开图可得其直观图,如图所示.
其中AC⊥CD,AC⊥CB,CD⊥CB,AC=CD=CB=2,
又BC∩CD=C,BC,CD 平面BCD,所以AC⊥平面BCD,
(2)如图所示是一个底面半径和高分别为1和4的圆柱形开口容器(下表面密封),P是母线BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一米粒,若这只蚂蚁要先爬到上口边缘再爬到点P处取得米粒,则它所需经过的最短路程为
√
依题意可得圆柱的底面半径r=1,高h=4,
将圆柱的侧面(一半)展开后得矩形ABCD,其中AB=π,
AD=4,
问题转化为在CD上找一点Q,使AQ+PQ最短,
作P关于CD的对称点E,连接AE,AE与CD交于点Q,
则得AQ+PQ的最小值就是
典例3 (1)(2022·新高考全国Ⅰ)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为36π,且3≤l≤ 则该正四棱锥体积的
取值范围是
考点三 多面体与球
√
方法一 如图,设该球的球心为O,半径为R,正四棱锥的底面边长为a,高为h,
依题意,得36π=
解得R=3.
方法二 如图,设该球的球心为O,半径为R,正四棱锥的底面边长为a,高为h,
依题意,得36π=
解得R=3.
方法三 如图,设该球的半径为R,球心为O,正四棱锥的底面边长为a,高为h,正四棱锥的侧棱与高所成的角为θ,
依题意,得36π=
解得R=3,
所以正四棱锥的底面边长a=
高h=lcos θ.
在△OPC中,作OE⊥PC,垂足为E,
所以l=6cos θ,
所以正四棱锥的体积
则y=sin θcos2θ=t(1-t2)=t-t3,
(2)(2023·南昌模拟)如图,在正四棱锥P-ABCD框架内放一个球O,球O与侧棱PA,PB,PC,PD均相切.若∠APB= 且OP=2,则球O的表面积为_____.
8π
在正四棱锥P-ABCD中,∠APB=
则△PAB是正三角形,
于是AC2=AB2+BC2=PA2+PC2,所以∠APC=
因为球O与侧棱PA,PB,PC,PD均相切,
则由对称性知,平面PAC截正四棱锥得等腰直角三角形,
截球O得球O的大圆,且圆O与直角边PA,PC都相切,如图,
显然OP平分∠APC,因此球O的半径R=
所以球O的表面积为4πR2=8π.
跟踪训练3 (1)(2022·全国乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为
√
该四棱锥的体积最大即以底面截球的圆面和顶点O组成的圆锥体积最大.
设圆锥的高为h(0
如图所示,
因为CC1⊥AC,AA1⊥BC CC1⊥BC,AC∩BC=C,AC,BC 平面ABC,
所以CC1⊥平面ABC,
又因为平面A1BC⊥平面AA1B,
平面A1BC∩平面AA1B=A1B,
过点A作AE⊥A1B,
则AE⊥平面A1BC,
则AE⊥BC,
又因为AA1⊥BC,AA1∩AE=A,AA1,AE 平面ABB1A1,
所以BC⊥平面ABB1A1,
又AB 平面ABB1A1,
所以AB⊥BC.
设AB=c,AC=b,BC=a,
则b2=a2+c2,
又因为三棱柱内切球的体积为
设内切球的半径为R,
解得ac=12,因为棱柱的高等于内切球直径2,
故三棱锥A-A1BC的体积为4.
空间几何体在高考题中主要考查表面积、体积问题,常见题型求解思路有两种,一是对于规则的几何体直接使用公式法求解,二是将不规则的几何体分解成基本的柱、锥、台体,先求这些柱、锥、台体的表面积或体积,再通过求和或作差得不规则几何体的表面积或体积.
提醒:组合体的表面积问题注意衔接部分的处理.旋转体的表面积问题注意其侧面展开图的应用.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
1.(2023·深圳模拟)圆锥侧面展开图扇形的圆心角为60°,底面圆的半径为8,则圆锥的侧面积为
A.384π B.392π C.398π D.404π
√
设圆锥的半径为r,母线长为l,则r=8,
由题意知,2πr=
解得l=48,
所以圆锥的侧面积为πrl=8×48π=384π.
1
2
3
4
5
6
7
8
9
10
11
12
2.(2023·惠州模拟)如图1,在高为h的直三棱柱容器ABC-A1B1C1中,AB=AC=2,AB⊥AC.现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为△A1B1C(如图2),则容器的高h为
A. B.3 C.4 D.6
√
1
2
3
4
5
6
7
8
9
10
11
12
由图2知 ,
其中h表示三棱柱的高,
故
,
因此,无水部分体积与有水部分体积之比为1∶2,所以图1中高度之比为1∶2,则h=3.
1
2
3
4
5
6
7
8
9
10
11
12
3.(2023·日照模拟)红灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼,营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上、下两部分是两个相同的圆柱的侧面,中间是球面除去上、下两个相同球冠剩下的部分.如图2,球冠是由球面被平面截得的一部分,垂直于截面的直径被截得的部分叫做球冠的高,若球冠所在球面的半径为R,球冠的高为h,则球冠的面积S=2πRh.如图1,已知该灯笼的高为58 cm,圆柱的高为5 cm,圆柱的底面圆直径为
14 cm,则围成该灯笼中间球面部分所
需布料的面积为
A.1 940π cm2 B.2 350π cm2
C.2 400π cm2 D.2 540π cm2
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
所以两个球冠的面积为2S=2×2πRh
=2×2×π×25×1=100π(cm2),
则围成该灯笼中间球面部分所需布料
的面积为4πR2-2S=4×π×252-100π=2 400π(cm2).
1
2
3
4
5
6
7
8
9
10
11
12
4.(2023·娄底模拟) 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=CA=AA1,点D是棱AA1上的点,AD= AA1,若截面BDC1分这个棱柱为两部分,则这两部分的体积比为
A.1∶2 B.4∶5
C.4∶9 D.5∶7
√
1
2
3
4
5
6
7
8
9
10
11
12
不妨令AB=BC=CA=AA1=4,且上、下底面为等边三角形,
又AA1⊥底面ABC,易知三棱柱ABC-A1B1C1为直三棱柱,所以侧面为正方形,
所以三棱柱ABC-A1B1C1的体积V=AA1·S△ABC=
而AD=1,CC1=4,故 = AC·(AD+CC1)=10,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
5.(2023·佛山模拟)科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,极目一号(如图1)是中国科学院空天信息研究院自主研发的系留浮空器.截至2022年5月,“极目一号”Ⅲ型浮空艇成功完成10次升空大气科学观测,最高升空至9 050 m,超过珠穆朗玛峰,创造了浮空艇原位大气科学观测海拔最高的世界纪录,彰显了中国的实力.“极目一号”Ⅲ型浮空艇长55 m,高19 m,若将它近似看作一个半球、一个圆柱和一个圆台的组合体,正视图如图2所示,则“极目一号”Ⅲ型浮空艇的体积约为(参考数据:9.52≈90,9.53≈857,315×1 005≈
316 600,π≈3.14)
A.9 064 m3 B.9 004 m3
C.8 944 m3 D.8 884 m3
√
1
2
3
4
5
6
7
8
9
10
11
12
V圆柱=π×9.52×14≈1 260π(m3),
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
由题可知矩形ABCD所在截面圆的半径r即为矩形ABCD的对角线长度的一半,
√
√
1
2
3
4
5
6
7
8
9
10
11
12
7.(多选)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台O1O2,在轴截面ABCD中,AB=AD=BC=2 cm,且CD=2AB,则
A.该圆台的高为1 cm
D.一只小虫从点C沿着该圆台的侧面爬行到AD的中点,所经过的最短路
程为5 cm
√
1
2
3
4
5
6
7
8
9
10
11
12
由圆台补成圆锥,可得大圆锥的母线长为4 cm,底面半径为2 cm,侧
面展开图的圆心角θ= =π,
1
2
3
4
5
6
7
8
9
10
11
12
设P为AD的中点,连接CP,如图2,可得∠COD= OC=4 cm,OP=3 cm,
则CP= =5(cm),从点C沿着该圆台的侧面爬行到AD的中点,所经过的最短路程为5 cm,故D正确.
8.(多选)(2023·新高考全国Ⅰ)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有
A.直径为0.99 m的球体
B.所有棱长均为1.4 m的四面体
C.底面直径为0.01 m,高为1.8 m的圆柱体
D.底面直径为1.2 m,高为0.01 m的圆柱体
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
对于A,因为0.99 m<1 m,即球体的直径小于正方体的棱长,
所以能够被整体放入正方体内,故A正确;
1
2
3
4
5
6
7
8
9
10
11
12
所以能够被整体放入正方体内,故B正确;
所以不能够被整体放入正方体内,故C错误;
对于D,
因为1.2 m>1 m,可知底面正方形不能包含圆
柱的底面圆,如图,
过AC1的中点O作OE⊥AC1,
设OE∩AC=E,
1
2
3
4
5
6
7
8
9
10
11
12
所以以AC1为轴可能对称放置底面直径为1.2 m的圆柱,
若底面直径为1.2 m的圆柱与正方体的上下底面均相切,
设圆柱的底面圆心为O1,与正方体下底面的切点为M,
可知AC1⊥O1M,O1M=0.6,
1
2
3
4
5
6
7
8
9
10
11
12
根据对称性可知圆柱的高为
所以能够被整体放入正方体内,所以D正确.
9.(2023·辽阳模拟)将3个6 cm×6 cm的正方形都沿其中的一对邻边的中点剪开,每个正方形均分成两个部分,如图(1)所示,将这6个部分接入一个边长为 的正六边形上,如图(2)所示.若该平面图沿着正六边形
的边折起,围成一个七面体,则该七面体的体积为_____ cm3.
108
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
将平面图形折叠并补形得到如图所示的正方体,
该七面体为正方体沿着图中的六边形截面截去一部分后剩下的另一部分,由对称性知其体积为正方体体积的一半,即 ×63=108(cm3).
10.棱长为2的正方体ABCD-A1B1C1D1中,M,N分别为棱BB1,AB的中点,则三棱锥A1-D1MN的体积为____.
1
1
2
3
4
5
6
7
8
9
10
11
12
如图,由正方体棱长为2,
1
2
3
4
5
6
7
8
9
10
11
12
又易知D1A1为三棱锥D1-A1MN的高,且D1A1=2,
∴
11.如图,在多面体ABCEF中,D为AB的中点,四边形CDFE为矩形,且DF⊥AB,AC=BC=2,∠ACB=120°,当AE⊥BE时,多面体ABCEF
的体积为_____.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
在△ABC中,因为AC=BC且D为AB的中点,所以CD⊥AB,
又因为DF⊥AB,且DF∩CD=D,DF,CD 平面CDFE,所以AB⊥平面CDFE,
在△ABC中,因为AC=BC=2且∠ACB=120°,CD⊥AB,
因为四边形CDFE为矩形,可得DF⊥CD,
又因为DF⊥AB,AB∩CD=D,AB,CD 平面ABC,所以DF⊥平面ABC,
1
2
3
4
5
6
7
8
9
10
11
12
因为CE∥DF,所以CE⊥平面ABC,
又因为AC,BC 平面ABC,所以CE⊥AC,CE⊥BC,
设CE=m,在Rt△ACE中,可得AE2=AC2+m2=4+m2,
在Rt△BCE中,可得BE2=BC2+m2=4+m2,
因为AE⊥BE,所以AB2=AE2+BE2,即12=4+m2+4+m2,解得m=
所以多面体ABCEF的体积
1
2
3
4
5
6
7
8
9
10
11
12
12.(2023·济宁模拟)l,l′为两条直线,α,β为两个平面,满足:l∩l′=O,l与l′的夹角为 α∥β,l⊥α,α与β之间的距离为2.以l为轴将l′旋
转一周,并用α,β截取得到两个同顶点O(点O在平面α与β之间)的圆锥.设
这两个圆锥的体积分别为V1,V2,则V1+V2的最小值为_____.
两个圆锥的轴截面如图所示,O1,O2分别为两圆锥的底面圆的圆心,
设半径分别为r1,r2,
O1O2⊥DE,O1O2⊥BC,
设OO1=h,因为α与β之间的距离为2,所以OO2=2-h,
1
2
3
4
5
6
7
8
9
10
11
12
由圆锥的性质知,OB=OC,OD=OE,
所以△ODE,△OBC为等边三角形,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
所以当h∈(0,1)时,f′(h)<0;
当h∈(1,2)时,f′(h)>0,
所以f(h)在(0,1)上单调递减,在(1,2)单调递增,
同课章节目录
