高考数学专题四立体几何 微专题27 空间角的计算 课件(共84张PPT)
文档属性
| 名称 | 高考数学专题四立体几何 微专题27 空间角的计算 课件(共84张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览









文档简介
(共84张PPT)
专题四 立体几何
微专题27
空间角的计算
以空间几何体为载体考查空间角是高考命题的重点.空间向量是将空间几何问题坐标化的工具,利用空间向量求平面与平面的夹角或线面角是高考热点,通常以解答题的形式出现,难度中等.
考情分析
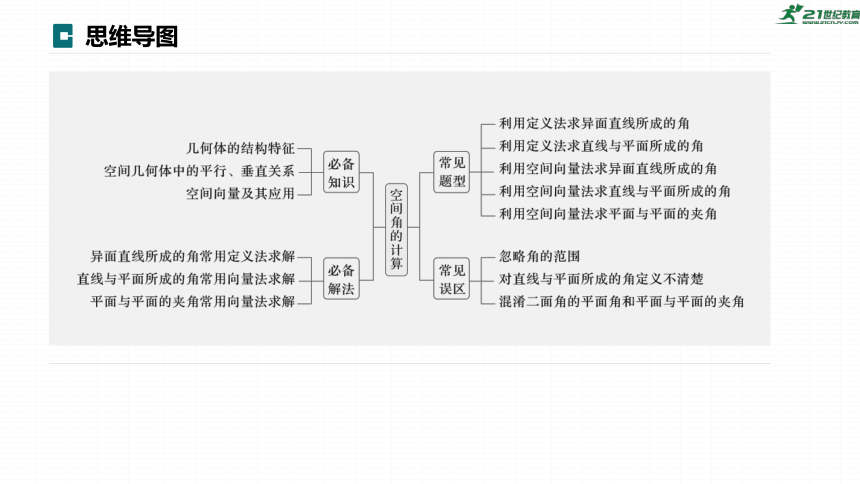
思维导图
内容索引
典型例题
热点突破
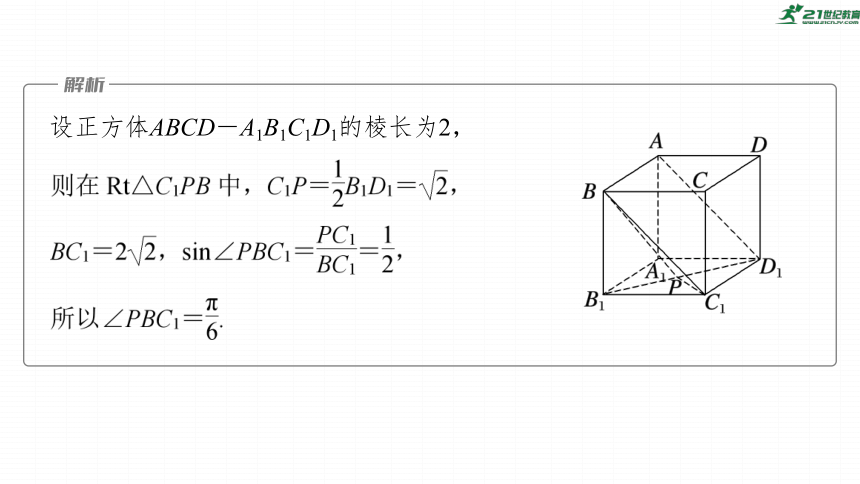
典例1 (2021·全国乙卷)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为
考点一 异面直线所成的角
√
方法一 如图,连接C1P,因为ABCD-A1B1C1D1是正方体,且P为B1D1的中点,所以C1P⊥B1D1,
又C1P⊥BB1,
B1D1∩BB1=B1,
所以C1P⊥平面B1BP.
又BP 平面B1BP,所以C1P⊥BP.
连接BC1,则AD1∥BC1,
所以∠PBC1为直线PB与AD1所成的角.
设正方体ABCD-A1B1C1D1的棱长为2,
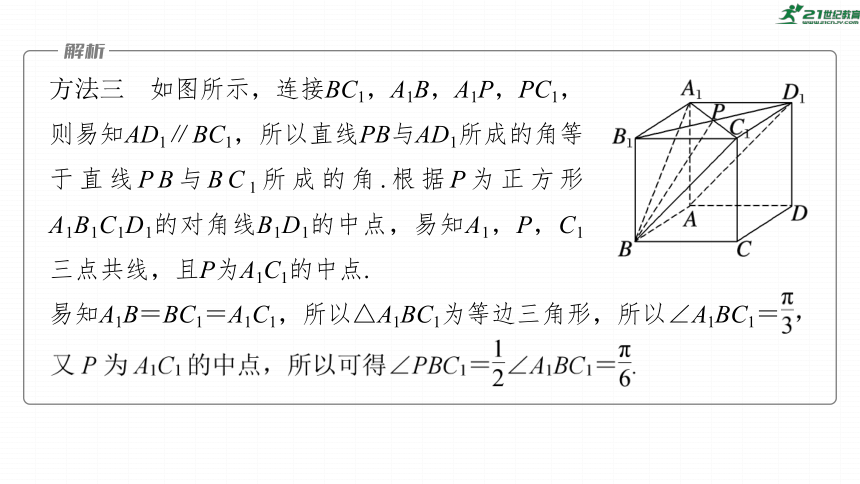
方法三 如图所示,连接BC1,A1B,A1P,PC1,则易知AD1∥BC1,所以直线PB与AD1所成的角等于直线PB与BC1所成的角.根据P为正方形A1B1C1D1的对角线B1D1的中点,易知A1,P,C1三点共线,且P为A1C1的中点.
易知A1B=BC1=A1C1,所以△A1BC1为等边三角形,所以∠A1BC1=
跟踪训练1 (2023·许昌模拟)已知三棱锥P-ABC中,PA⊥平面ABC,AB=4,AC=4,BC= PA=6,D为PB的中点,则异面直线AD与PC所
成角的余弦值为
√
如图所示,取BC的中点E,连接AE,DE,
则DE∥PC,∠ADE(或其补角)即为异面直线AD与PC所成的角.
由AB=4,AC=4,BC= 得AB2+AC2=BC2,所以AB⊥AC,
又E为BC的中点,则AE= PA⊥平面ABC,
在△ADE中,根据余弦定理可得
典例2 (2023·潍坊模拟)如图,圆台O1O2的上底面半径为1,下底面半径为 AB为圆台下底面的一条直径,圆O2上点C满足AC=BC,PO1是圆台上底面的一条半径,点P,C在平面ABO1的同侧,且PO1∥BC.
(1)证明:O1O2∥平面PAC;
考点二 直线与平面所成的角
取AC的中点M,连接O2M,PM,如图,
故PO1∥O2M,PO1=O2M,
所以四边形PO1O2M为平行四边形,
则PM∥O1O2,又PM 平面PAC,O1O2 平面PAC,
故O1O2∥平面PAC.
(2)从条件①、条件②中选择一个作为已知,求直线AO1与平面PBC所成角的正弦值.
条件①:三棱锥O1-ABC的体积为
条件②:AO1与圆台底面所成角的正切值为
注:如果选择条件①和条件②分别解答,按第一个解答计分.
又O1O2⊥平面ABC,
所以O1O2=2.
以O2为坐标原点,O2B,O2C,O2O1所在直线为坐标轴建立如图所示的空间直角坐标系.
设平面PBC的法向量为n=(x,y,z),
设所求角的大小为θ,
选条件②:因为O1O2⊥平面ABC,
所以∠O1AO2为AO1与圆台底面所成的角,
下同条件①.
跟踪训练2 (2022·全国乙卷)4如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
因为AD=CD,E为AC的中点,所以AC⊥DE.
在△ADB和△CDB中,
因为AD=CD,∠ADB=∠CDB,DB=DB,
所以△ADB≌△CDB,所以AB=BC.
因为E为AC的中点,所以AC⊥BE.
又BE∩DE=E,BE,DE 平面BED,
所以AC⊥平面BED,
又AC 平面ACD,
所以平面BED⊥平面ACD.
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
由(1)可知AB=BC,
又∠ACB=60°,AB=2,
所以△ABC为边长为2的正三角形,
则AC=2,BE= AE=1.
因为AD=CD,AD⊥CD,
所以△ADC为等腰直角三角形,
所以DE=1.
所以DE2+BE2=BD2,则DE⊥BE.
由(1)可知,AC⊥平面BED.
连接EF,因为EF 平面BED,
所以AC⊥EF,
当△AFC的面积最小时,点F到直线AC的距离最小,
即EF的长度最小.
在Rt△BED中,当EF的长度最小时,
方法一 由(1)可知,DE⊥AC,BE⊥AC,
所以EA,EB,ED两两垂直,
以E为坐标原点,EA,EB,ED所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系,则A(1,0,0),B(0, 0),D(0,0,1),C(-1,0,0),
设平面ABD的法向量为n=(x1,y1,z1),
记CF与平面ABD所成的角为α,
方法二 因为E为AC的中点,所以点C到平面ABD的距离等于点E到平面ABD的距离的2倍.
因为DE⊥AC,DE⊥BE,AC∩BE=E,AC,BE 平面ABC,
所以DE⊥平面ABC.
因为VD-AEB=VE-ADB,
因为AC⊥平面BED,EF 平面BED,
所以AC⊥EF,
记CF与平面ABD所成的角为α,
方法三 如图,过点E作EM⊥AB交AB于点M,连接DM,过点E作EG⊥DM交DM于点G.
因为DE⊥AC,DE⊥BE,AC∩BE=E,
AC,BE 平面ABC,
所以DE⊥平面ABC,又AB 平面ABC,
所以DE⊥AB,
又EM∩DE=E,EM,DE 平面DEM,所以AB⊥平面DEM,
又EG 平面DEM,所以AB⊥EG,
又AB∩DM=M,AB,DM 平面ABD,
所以EG⊥平面ABD,则EG的长度等于点E到平面ABD的距离.
因为E为AC的中点,所以EG的长度等于点C到平面ABD的距离的
记CF与平面ABD所成的角为α,
典例3 (2023·新高考全国Ⅰ)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.
(1)证明:B2C2∥A2D2;
考点三 平面与平面的夹角
以C为坐标原点,CD,CB,CC1所在直线分别为x,y,z轴建立空间直角坐标系,如图,
则C(0,0,0),C2(0,0,3),B2(0,2,2),D2(2,0,2),A2(2,2,1),
又B2C2,A2D2不在同一条直线上,∴B2C2∥A2D2.
(2)点P在棱BB1上,当二面角P-A2C2-D2为150°时,求B2P.
设P(0,2,λ)(0≤λ≤4),
设平面PA2C2的法向量为n=(x,y,z),
令 z=2,得y=3-λ,x=λ-1,
∴n=(λ-1,3-λ,2),
设平面A2C2D2的法向量为m=(a,b,c),
令a=1,得b=1,c=2,
∴m=(1,1,2),
化简可得,λ2-4λ+3=0,解得λ=1或λ=3,
∴P(0,2,3)或P(0,2,1),∴B2P=1.
跟踪训练3 (2023·唐山模拟)如图,在三棱柱ABC-A1B1C1中,侧面A1B1BA和侧面A1ACC1均为正方形,D为棱BC的中点.
(1)证明:平面ADC1⊥平面B1BCC1;
因为侧面A1B1BA和侧面A1ACC1均为正方形,
所以A1A⊥AB,A1A⊥AC,又AB∩AC=A,AB,
AC 平面ABC,
所以A1A⊥平面ABC,又A1A∥C1C,所以C1C⊥
平面ABC,
又AD 平面ABC,所以C1C⊥AD.
由AB=AC,D为棱BC的中点,所以AD⊥BC,
又BC∩CC1=C,BC,CC1 平面B1BCC1,
因此AD⊥平面B1BCC1,又AD 平面ADC1,
故平面ADC1⊥平面B1BCC1.
(2)若直线AC1与平面B1BCC1所成角为30°,求平面A1B1BA与平面ADC1夹角的余弦值.
由(1)得∠AC1D是AC1与平面B1BCC1所成角,即∠AC1D=30°,
则∠DAC=45°,∠BAC=90°.
以A为原点,以 的方向分别为x轴,
y轴,z轴的正方向,建立如图所示的空间直角坐标系,
设m=(x,y,z)是平面ADC1的法向量,
易知n=(0,1,0)是平面A1B1BA的一个法向量,
总结提升
1.(2023·丹东质检)设C′与C分别为圆柱上、下底面圆周上的点,且位于该圆柱轴截面ABB′A′同侧,下底面圆心O在AB上,若 = ,
,cos∠C′CO= 则直线CC′与AB所成角的余弦值为
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
设圆柱的底面半径为r,高为h,过C′作C′D∥B′B,连接C′O,OD,CD,
由题设弧长的数量关系知,△OCD为边长为r的正三角形且CD∥AB,C′D垂直于圆柱底面,
1
2
3
4
5
6
7
8
9
10
因为CD∥AB,所以∠C′CD即为异面直线CC′
与AB所成的角(或其补角).
2.(2023·合肥模拟)米斗是称量粮食的量器,是古代官仓、粮栈、米行及地主家里必备的用具,如图为一倒正四棱台形米斗,高为40 cm.已知该正四棱台的所有顶点都在一个半径为50 cm的球O的球面上,且一个底面的中心与球O的球心重合,则该正四棱台的侧棱与底面所成角的正弦值为
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
由题意,作出正四棱台的对角面,如图,
AD为正四棱台上底面正方形对角线,BC为正四
棱台下底面正方形对角线,
O为外接球球心,为线段BC的中点,则OD=OA=OB=OC=50,
过点D作DE⊥BC,垂足为E,则∠DCE即为所求角.
因为OD=50,DE=40,所以OE=30,EC=20,
3.在三棱锥P-ABC中,△ABC和△PBC均为等边三角形,且二面角P-BC-A的大小为120°,则异面直线PB和AC所成角的余弦值为
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
方法一 如图,取BC的中点O,连接OP,OA.
因为△ABC和△PBC均为等边三角形,
所以AO⊥BC,PO⊥BC,
所以BC⊥平面PAO,即平面PAO⊥平面ABC.
所以∠POA就是二面角P-BC-A的平面角,即∠POA=120°,
建立空间直角坐标系,如图所示.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
方法二 如图所示,取BC的中点O,连接OP,OA.
因为△ABC和△PBC是全等的等边三角形,
所以AO⊥BC,PO⊥BC,
所以∠POA就是二面角的平面角.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
4.(2023·莆田模拟)在正方体ABCD-A1B1C1D1中,点M,N分别是A1C,BD上的动点,当线段MN的长最小时,直线MN与平面BCC1B1所成角的正弦值为
√
1
2
3
4
5
6
7
8
9
10
以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
因为AA1⊥平面ABCD,BD 平面ABCD,
所以AA1⊥BD,
因为在正方形ABCD中,AC ⊥ BD,且AC∩AA1
=A,AC,AA1 平面A1AC,
所以BD⊥平面A1AC,
因为点M,N分别是A1C,BD上的动点,
当点N为AC,BD的交点时,MN⊥BD,过点N作NM⊥ A1C于点M,
1
2
3
4
5
6
7
8
9
10
此时MN为A1C,BD的公垂线,即线段MN的长最小,
1
2
3
4
5
6
7
8
9
10
设MN与平面BCC1B1所成角的大小为θ,
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·潍坊模拟)如图所示的几何体,是将棱长为3的正四面体沿棱的三等分点,作平行于底面的截面所得,且其所有棱长均为1,则
√
√
1
2
3
4
5
6
7
8
9
10
将该几何体还原为原正四面体Q-MNS,棱长为3,
设△MNS的中心为O,连接OQ,ON,
1
2
3
4
5
6
7
8
9
10
对于C,该几何体的体积为大正四面体的体积减去4个棱长为1的小正四面体的体积,易得小正
四面体的体积为
对于D,二面角A-BC-D的平面角与A-BC-Q的平面角互补,显然二面角A-BC-Q为锐角,所以二面角A-BC-D一定为钝角,其余弦值为负数,故D错误.
1
2
3
4
5
6
7
8
9
10
√
√
1
2
3
4
5
6
7
8
9
10
以O为原点,分别以OA,OS所在直线为x,z轴,
建立如图所示的空间直角坐标系,
则S(0,0, ),A(1,0,0),
设B(m,n,0),且m2+n2=3,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
得m2=9>3,不符合题意,故B错误;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
则p·q=0,
又m2+n2=3,得m=3,m2=9>3,不符合题意,故D错误.
1
2
3
4
5
6
7
8
9
10
7.过正方形ABCD的顶点A作PA⊥平面ABCD,若AB=PA,则平面PAB与平面PCD夹角的大小为________.
45°
1
2
3
4
5
6
7
8
9
10
如图,建立空间直角坐标系,
设AB=PA=1,
则A(0,0,0),D(0,1,0),P(0,0,1),
由题意,AD⊥平面PAB,设E为PD的中点,
连接AE,则AE⊥PD,
又CD⊥平面PAD,
∴CD⊥AE,又PD∩CD=D,从而AE⊥平面PCD.
1
2
3
4
5
6
7
8
9
10
故平面PAB与平面PCD夹角的大小为45°.
8.(2023·湖北黄冈中学模拟)在空间四面体ABCD中,∠ACD=60°,二面角A-CD-B的大小为45°,在平面ABC内过点B作AC的垂线l,则l与平
面BCD所成的最大角的正弦值为______.
1
2
3
4
5
6
7
8
9
10
如图,记过点B作AC的垂线l,垂足为E,
过点E作BC的垂线EH,垂足为H,
过点H作CD的垂线HG,垂足为G,连接EG.
过点E作垂直于直线CE的平面α,α交平面BCD于直线BF,F在CD上,
则当BF⊥平面ABC时,l与平面BCD所成的角最大,且与∠ECH互余.
因为BF⊥平面ABC,EH 平面ABC,
所以BF⊥EH,
又EH⊥BC,BC∩BF=B,BC,BF 平面BCD,
所以EH⊥平面BCD,
1
2
3
4
5
6
7
8
9
10
所以l与平面BCD所成的角即为∠EBH.
因为CD⊥GH,CD⊥EH,GH∩EH=H,GH,EH 平面EHG,
所以CD⊥平面EHG,
又EG 平面EHG,
所以CD⊥EG,
所以∠EGH即为二面角A-CD-B的平面角,即∠EGH=45°,
设GH=m,
1
2
3
4
5
6
7
8
9
10
又∠ACG=60°,
1
2
3
4
5
6
7
8
9
10
记此时l与平面BCD所成角为θ,
9.(2023·宣城模拟)如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA=PD,PB=PC=BC=2,二面角P-BC-A的大小为30°.
(1)证明:平面PAD⊥平面PBC;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
设AD,BC的中点分别为E,F,连接EF,PE,PF,
因为底面ABCD是正方形,PB=PC,
所以EF⊥BC,PF⊥BC,
又EF∩PF=F,EF,PF 平面PEF,
所以BC⊥平面PEF,
又PE 平面PEF,
所以BC⊥PE.
由题意知∠PFE是二面角P-BC-A的平面角,
1
2
3
4
5
6
7
8
9
10
所以PE2+PF2=EF2,
所以PF⊥PE,
又PF∩BC=F,PF,BC 平面PBC,
所以PE⊥平面PBC,
因为PE 平面PAD,
所以平面PAD⊥平面PBC.
(2)求PC与平面PAB所成角的正弦值.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
由(1)知平面PEF⊥平面PAD,以E为坐标原点,EA所在直线为x轴,EF所在直线为y轴,建立空间直角坐标系,如图所示,
则A(1,0,0),B(1,2,0),C(-1,2,0),
设平面PAB的法向量为n=(x,y,z),则
1
2
3
4
5
6
7
8
9
10
设PC与平面PAB所成的角为θ,则
10.(2023·武汉调研) 如图,在三棱柱ABC-A1B1C1中,AC= AB=1,E,F分别为A1C,BB1的中点,且EF⊥平面AA1C1C.
(1)求棱BC的长度;
1
2
3
4
5
6
7
8
9
10
如图,取AC的中点D,连接ED,BD,
∵D,E分别为AC,A1C的中点,则DE∥AA1且
DE=
又∵F为BB1的中点,则BF∥AA1且BF=
可得DE∥BF且DE=BF,即四边形DEFB为平行四边形,故EF∥DB,
∵EF⊥平面AA1C1C,∴DB⊥平面AA1C1C,
又AC 平面AA1C1C,可得DB⊥AC,
又∵D为AC的中点,则△ABC为等腰三角形,
∴BC=AB=1.
1
2
3
4
5
6
7
8
9
10
(2)若BB1⊥A1B1,且△A1FC的面积 =
求二面角B1-A1F-C的正弦值.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
由(1)可知,BC=AB=1,且AC=
即AB2+BC2=AC2,
∴AB⊥BC,
∵EF⊥平面AA1C1C,A1C 平面AA1C1C,则EF⊥A1C,
由(1)知DB⊥平面AA1C1C,AA1 平面AA1C1C,则DB⊥AA1,
又∵AA1∥BB1,则DB⊥BB1,
1
2
3
4
5
6
7
8
9
10
∵BB1⊥A1B1,AB∥A1B1,则BB1⊥AB,
又AB∩DB=B,AB,DB 平面ABC,
∴BB1⊥平面ABC,
AC 平面ABC,则BB1⊥AC,
∵AA1∥BB1,∴AA1⊥AC,
∴△AA1C为直角三角形,
1
2
3
4
5
6
7
8
9
10
设平面A1FC的法向量为n1=(x,y,z),
由题意知,平面B1A1F的一个法向量为n2=(1,0,0),
1
2
3
4
5
6
7
8
9
10
设二面角B1-A1F-C的平面角为θ∈(0,π),
专题四 立体几何
微专题27
空间角的计算
以空间几何体为载体考查空间角是高考命题的重点.空间向量是将空间几何问题坐标化的工具,利用空间向量求平面与平面的夹角或线面角是高考热点,通常以解答题的形式出现,难度中等.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (2021·全国乙卷)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为
考点一 异面直线所成的角
√
方法一 如图,连接C1P,因为ABCD-A1B1C1D1是正方体,且P为B1D1的中点,所以C1P⊥B1D1,
又C1P⊥BB1,
B1D1∩BB1=B1,
所以C1P⊥平面B1BP.
又BP 平面B1BP,所以C1P⊥BP.
连接BC1,则AD1∥BC1,
所以∠PBC1为直线PB与AD1所成的角.
设正方体ABCD-A1B1C1D1的棱长为2,
方法三 如图所示,连接BC1,A1B,A1P,PC1,则易知AD1∥BC1,所以直线PB与AD1所成的角等于直线PB与BC1所成的角.根据P为正方形A1B1C1D1的对角线B1D1的中点,易知A1,P,C1三点共线,且P为A1C1的中点.
易知A1B=BC1=A1C1,所以△A1BC1为等边三角形,所以∠A1BC1=
跟踪训练1 (2023·许昌模拟)已知三棱锥P-ABC中,PA⊥平面ABC,AB=4,AC=4,BC= PA=6,D为PB的中点,则异面直线AD与PC所
成角的余弦值为
√
如图所示,取BC的中点E,连接AE,DE,
则DE∥PC,∠ADE(或其补角)即为异面直线AD与PC所成的角.
由AB=4,AC=4,BC= 得AB2+AC2=BC2,所以AB⊥AC,
又E为BC的中点,则AE= PA⊥平面ABC,
在△ADE中,根据余弦定理可得
典例2 (2023·潍坊模拟)如图,圆台O1O2的上底面半径为1,下底面半径为 AB为圆台下底面的一条直径,圆O2上点C满足AC=BC,PO1是圆台上底面的一条半径,点P,C在平面ABO1的同侧,且PO1∥BC.
(1)证明:O1O2∥平面PAC;
考点二 直线与平面所成的角
取AC的中点M,连接O2M,PM,如图,
故PO1∥O2M,PO1=O2M,
所以四边形PO1O2M为平行四边形,
则PM∥O1O2,又PM 平面PAC,O1O2 平面PAC,
故O1O2∥平面PAC.
(2)从条件①、条件②中选择一个作为已知,求直线AO1与平面PBC所成角的正弦值.
条件①:三棱锥O1-ABC的体积为
条件②:AO1与圆台底面所成角的正切值为
注:如果选择条件①和条件②分别解答,按第一个解答计分.
又O1O2⊥平面ABC,
所以O1O2=2.
以O2为坐标原点,O2B,O2C,O2O1所在直线为坐标轴建立如图所示的空间直角坐标系.
设平面PBC的法向量为n=(x,y,z),
设所求角的大小为θ,
选条件②:因为O1O2⊥平面ABC,
所以∠O1AO2为AO1与圆台底面所成的角,
下同条件①.
跟踪训练2 (2022·全国乙卷)4如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
因为AD=CD,E为AC的中点,所以AC⊥DE.
在△ADB和△CDB中,
因为AD=CD,∠ADB=∠CDB,DB=DB,
所以△ADB≌△CDB,所以AB=BC.
因为E为AC的中点,所以AC⊥BE.
又BE∩DE=E,BE,DE 平面BED,
所以AC⊥平面BED,
又AC 平面ACD,
所以平面BED⊥平面ACD.
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
由(1)可知AB=BC,
又∠ACB=60°,AB=2,
所以△ABC为边长为2的正三角形,
则AC=2,BE= AE=1.
因为AD=CD,AD⊥CD,
所以△ADC为等腰直角三角形,
所以DE=1.
所以DE2+BE2=BD2,则DE⊥BE.
由(1)可知,AC⊥平面BED.
连接EF,因为EF 平面BED,
所以AC⊥EF,
当△AFC的面积最小时,点F到直线AC的距离最小,
即EF的长度最小.
在Rt△BED中,当EF的长度最小时,
方法一 由(1)可知,DE⊥AC,BE⊥AC,
所以EA,EB,ED两两垂直,
以E为坐标原点,EA,EB,ED所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系,则A(1,0,0),B(0, 0),D(0,0,1),C(-1,0,0),
设平面ABD的法向量为n=(x1,y1,z1),
记CF与平面ABD所成的角为α,
方法二 因为E为AC的中点,所以点C到平面ABD的距离等于点E到平面ABD的距离的2倍.
因为DE⊥AC,DE⊥BE,AC∩BE=E,AC,BE 平面ABC,
所以DE⊥平面ABC.
因为VD-AEB=VE-ADB,
因为AC⊥平面BED,EF 平面BED,
所以AC⊥EF,
记CF与平面ABD所成的角为α,
方法三 如图,过点E作EM⊥AB交AB于点M,连接DM,过点E作EG⊥DM交DM于点G.
因为DE⊥AC,DE⊥BE,AC∩BE=E,
AC,BE 平面ABC,
所以DE⊥平面ABC,又AB 平面ABC,
所以DE⊥AB,
又EM∩DE=E,EM,DE 平面DEM,所以AB⊥平面DEM,
又EG 平面DEM,所以AB⊥EG,
又AB∩DM=M,AB,DM 平面ABD,
所以EG⊥平面ABD,则EG的长度等于点E到平面ABD的距离.
因为E为AC的中点,所以EG的长度等于点C到平面ABD的距离的
记CF与平面ABD所成的角为α,
典例3 (2023·新高考全国Ⅰ)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.
(1)证明:B2C2∥A2D2;
考点三 平面与平面的夹角
以C为坐标原点,CD,CB,CC1所在直线分别为x,y,z轴建立空间直角坐标系,如图,
则C(0,0,0),C2(0,0,3),B2(0,2,2),D2(2,0,2),A2(2,2,1),
又B2C2,A2D2不在同一条直线上,∴B2C2∥A2D2.
(2)点P在棱BB1上,当二面角P-A2C2-D2为150°时,求B2P.
设P(0,2,λ)(0≤λ≤4),
设平面PA2C2的法向量为n=(x,y,z),
令 z=2,得y=3-λ,x=λ-1,
∴n=(λ-1,3-λ,2),
设平面A2C2D2的法向量为m=(a,b,c),
令a=1,得b=1,c=2,
∴m=(1,1,2),
化简可得,λ2-4λ+3=0,解得λ=1或λ=3,
∴P(0,2,3)或P(0,2,1),∴B2P=1.
跟踪训练3 (2023·唐山模拟)如图,在三棱柱ABC-A1B1C1中,侧面A1B1BA和侧面A1ACC1均为正方形,D为棱BC的中点.
(1)证明:平面ADC1⊥平面B1BCC1;
因为侧面A1B1BA和侧面A1ACC1均为正方形,
所以A1A⊥AB,A1A⊥AC,又AB∩AC=A,AB,
AC 平面ABC,
所以A1A⊥平面ABC,又A1A∥C1C,所以C1C⊥
平面ABC,
又AD 平面ABC,所以C1C⊥AD.
由AB=AC,D为棱BC的中点,所以AD⊥BC,
又BC∩CC1=C,BC,CC1 平面B1BCC1,
因此AD⊥平面B1BCC1,又AD 平面ADC1,
故平面ADC1⊥平面B1BCC1.
(2)若直线AC1与平面B1BCC1所成角为30°,求平面A1B1BA与平面ADC1夹角的余弦值.
由(1)得∠AC1D是AC1与平面B1BCC1所成角,即∠AC1D=30°,
则∠DAC=45°,∠BAC=90°.
以A为原点,以 的方向分别为x轴,
y轴,z轴的正方向,建立如图所示的空间直角坐标系,
设m=(x,y,z)是平面ADC1的法向量,
易知n=(0,1,0)是平面A1B1BA的一个法向量,
总结提升
1.(2023·丹东质检)设C′与C分别为圆柱上、下底面圆周上的点,且位于该圆柱轴截面ABB′A′同侧,下底面圆心O在AB上,若 = ,
,cos∠C′CO= 则直线CC′与AB所成角的余弦值为
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
设圆柱的底面半径为r,高为h,过C′作C′D∥B′B,连接C′O,OD,CD,
由题设弧长的数量关系知,△OCD为边长为r的正三角形且CD∥AB,C′D垂直于圆柱底面,
1
2
3
4
5
6
7
8
9
10
因为CD∥AB,所以∠C′CD即为异面直线CC′
与AB所成的角(或其补角).
2.(2023·合肥模拟)米斗是称量粮食的量器,是古代官仓、粮栈、米行及地主家里必备的用具,如图为一倒正四棱台形米斗,高为40 cm.已知该正四棱台的所有顶点都在一个半径为50 cm的球O的球面上,且一个底面的中心与球O的球心重合,则该正四棱台的侧棱与底面所成角的正弦值为
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
由题意,作出正四棱台的对角面,如图,
AD为正四棱台上底面正方形对角线,BC为正四
棱台下底面正方形对角线,
O为外接球球心,为线段BC的中点,则OD=OA=OB=OC=50,
过点D作DE⊥BC,垂足为E,则∠DCE即为所求角.
因为OD=50,DE=40,所以OE=30,EC=20,
3.在三棱锥P-ABC中,△ABC和△PBC均为等边三角形,且二面角P-BC-A的大小为120°,则异面直线PB和AC所成角的余弦值为
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
方法一 如图,取BC的中点O,连接OP,OA.
因为△ABC和△PBC均为等边三角形,
所以AO⊥BC,PO⊥BC,
所以BC⊥平面PAO,即平面PAO⊥平面ABC.
所以∠POA就是二面角P-BC-A的平面角,即∠POA=120°,
建立空间直角坐标系,如图所示.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
方法二 如图所示,取BC的中点O,连接OP,OA.
因为△ABC和△PBC是全等的等边三角形,
所以AO⊥BC,PO⊥BC,
所以∠POA就是二面角的平面角.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
4.(2023·莆田模拟)在正方体ABCD-A1B1C1D1中,点M,N分别是A1C,BD上的动点,当线段MN的长最小时,直线MN与平面BCC1B1所成角的正弦值为
√
1
2
3
4
5
6
7
8
9
10
以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
因为AA1⊥平面ABCD,BD 平面ABCD,
所以AA1⊥BD,
因为在正方形ABCD中,AC ⊥ BD,且AC∩AA1
=A,AC,AA1 平面A1AC,
所以BD⊥平面A1AC,
因为点M,N分别是A1C,BD上的动点,
当点N为AC,BD的交点时,MN⊥BD,过点N作NM⊥ A1C于点M,
1
2
3
4
5
6
7
8
9
10
此时MN为A1C,BD的公垂线,即线段MN的长最小,
1
2
3
4
5
6
7
8
9
10
设MN与平面BCC1B1所成角的大小为θ,
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·潍坊模拟)如图所示的几何体,是将棱长为3的正四面体沿棱的三等分点,作平行于底面的截面所得,且其所有棱长均为1,则
√
√
1
2
3
4
5
6
7
8
9
10
将该几何体还原为原正四面体Q-MNS,棱长为3,
设△MNS的中心为O,连接OQ,ON,
1
2
3
4
5
6
7
8
9
10
对于C,该几何体的体积为大正四面体的体积减去4个棱长为1的小正四面体的体积,易得小正
四面体的体积为
对于D,二面角A-BC-D的平面角与A-BC-Q的平面角互补,显然二面角A-BC-Q为锐角,所以二面角A-BC-D一定为钝角,其余弦值为负数,故D错误.
1
2
3
4
5
6
7
8
9
10
√
√
1
2
3
4
5
6
7
8
9
10
以O为原点,分别以OA,OS所在直线为x,z轴,
建立如图所示的空间直角坐标系,
则S(0,0, ),A(1,0,0),
设B(m,n,0),且m2+n2=3,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
得m2=9>3,不符合题意,故B错误;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
则p·q=0,
又m2+n2=3,得m=3,m2=9>3,不符合题意,故D错误.
1
2
3
4
5
6
7
8
9
10
7.过正方形ABCD的顶点A作PA⊥平面ABCD,若AB=PA,则平面PAB与平面PCD夹角的大小为________.
45°
1
2
3
4
5
6
7
8
9
10
如图,建立空间直角坐标系,
设AB=PA=1,
则A(0,0,0),D(0,1,0),P(0,0,1),
由题意,AD⊥平面PAB,设E为PD的中点,
连接AE,则AE⊥PD,
又CD⊥平面PAD,
∴CD⊥AE,又PD∩CD=D,从而AE⊥平面PCD.
1
2
3
4
5
6
7
8
9
10
故平面PAB与平面PCD夹角的大小为45°.
8.(2023·湖北黄冈中学模拟)在空间四面体ABCD中,∠ACD=60°,二面角A-CD-B的大小为45°,在平面ABC内过点B作AC的垂线l,则l与平
面BCD所成的最大角的正弦值为______.
1
2
3
4
5
6
7
8
9
10
如图,记过点B作AC的垂线l,垂足为E,
过点E作BC的垂线EH,垂足为H,
过点H作CD的垂线HG,垂足为G,连接EG.
过点E作垂直于直线CE的平面α,α交平面BCD于直线BF,F在CD上,
则当BF⊥平面ABC时,l与平面BCD所成的角最大,且与∠ECH互余.
因为BF⊥平面ABC,EH 平面ABC,
所以BF⊥EH,
又EH⊥BC,BC∩BF=B,BC,BF 平面BCD,
所以EH⊥平面BCD,
1
2
3
4
5
6
7
8
9
10
所以l与平面BCD所成的角即为∠EBH.
因为CD⊥GH,CD⊥EH,GH∩EH=H,GH,EH 平面EHG,
所以CD⊥平面EHG,
又EG 平面EHG,
所以CD⊥EG,
所以∠EGH即为二面角A-CD-B的平面角,即∠EGH=45°,
设GH=m,
1
2
3
4
5
6
7
8
9
10
又∠ACG=60°,
1
2
3
4
5
6
7
8
9
10
记此时l与平面BCD所成角为θ,
9.(2023·宣城模拟)如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA=PD,PB=PC=BC=2,二面角P-BC-A的大小为30°.
(1)证明:平面PAD⊥平面PBC;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
设AD,BC的中点分别为E,F,连接EF,PE,PF,
因为底面ABCD是正方形,PB=PC,
所以EF⊥BC,PF⊥BC,
又EF∩PF=F,EF,PF 平面PEF,
所以BC⊥平面PEF,
又PE 平面PEF,
所以BC⊥PE.
由题意知∠PFE是二面角P-BC-A的平面角,
1
2
3
4
5
6
7
8
9
10
所以PE2+PF2=EF2,
所以PF⊥PE,
又PF∩BC=F,PF,BC 平面PBC,
所以PE⊥平面PBC,
因为PE 平面PAD,
所以平面PAD⊥平面PBC.
(2)求PC与平面PAB所成角的正弦值.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
由(1)知平面PEF⊥平面PAD,以E为坐标原点,EA所在直线为x轴,EF所在直线为y轴,建立空间直角坐标系,如图所示,
则A(1,0,0),B(1,2,0),C(-1,2,0),
设平面PAB的法向量为n=(x,y,z),则
1
2
3
4
5
6
7
8
9
10
设PC与平面PAB所成的角为θ,则
10.(2023·武汉调研) 如图,在三棱柱ABC-A1B1C1中,AC= AB=1,E,F分别为A1C,BB1的中点,且EF⊥平面AA1C1C.
(1)求棱BC的长度;
1
2
3
4
5
6
7
8
9
10
如图,取AC的中点D,连接ED,BD,
∵D,E分别为AC,A1C的中点,则DE∥AA1且
DE=
又∵F为BB1的中点,则BF∥AA1且BF=
可得DE∥BF且DE=BF,即四边形DEFB为平行四边形,故EF∥DB,
∵EF⊥平面AA1C1C,∴DB⊥平面AA1C1C,
又AC 平面AA1C1C,可得DB⊥AC,
又∵D为AC的中点,则△ABC为等腰三角形,
∴BC=AB=1.
1
2
3
4
5
6
7
8
9
10
(2)若BB1⊥A1B1,且△A1FC的面积 =
求二面角B1-A1F-C的正弦值.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
由(1)可知,BC=AB=1,且AC=
即AB2+BC2=AC2,
∴AB⊥BC,
∵EF⊥平面AA1C1C,A1C 平面AA1C1C,则EF⊥A1C,
由(1)知DB⊥平面AA1C1C,AA1 平面AA1C1C,则DB⊥AA1,
又∵AA1∥BB1,则DB⊥BB1,
1
2
3
4
5
6
7
8
9
10
∵BB1⊥A1B1,AB∥A1B1,则BB1⊥AB,
又AB∩DB=B,AB,DB 平面ABC,
∴BB1⊥平面ABC,
AC 平面ABC,则BB1⊥AC,
∵AA1∥BB1,∴AA1⊥AC,
∴△AA1C为直角三角形,
1
2
3
4
5
6
7
8
9
10
设平面A1FC的法向量为n1=(x,y,z),
由题意知,平面B1A1F的一个法向量为n2=(1,0,0),
1
2
3
4
5
6
7
8
9
10
设二面角B1-A1F-C的平面角为θ∈(0,π),
同课章节目录
