高考数学专题五概率与统计 微专题31 计数原理与概率 课件(共54张PPT)
文档属性
| 名称 | 高考数学专题五概率与统计 微专题31 计数原理与概率 课件(共54张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:05:11 | ||
图片预览











文档简介
(共54张PPT)
专题五 概率与统计
微专题31
计数原理与概率
主要考查两个计数原理、排列、组合的简单应用,时常与概率相结合,以选择题、填空题为主.二项式定理主要考查通项公式、二项式系数等知识,近几年也与函数、不等式、数列交汇考查.概率重点考查古典概型、条件概率的基本应用.
考情分析
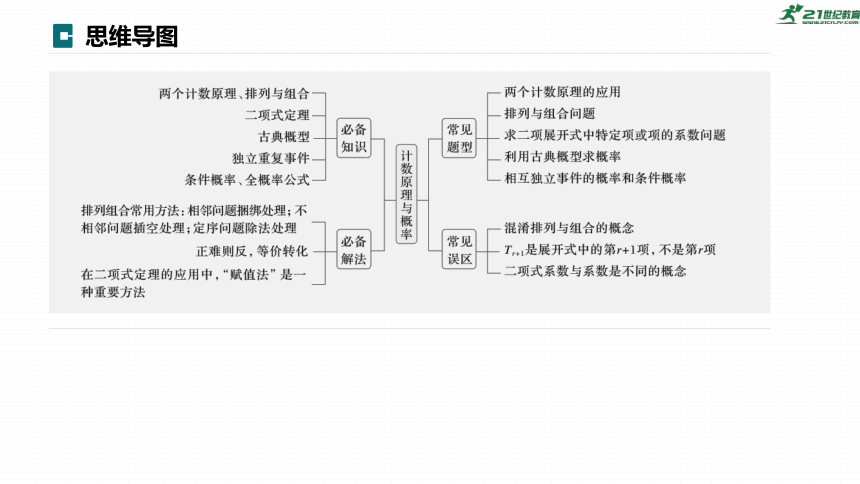
思维导图
内容索引
典型例题
热点突破
典例1 (1)(2023·新高考全国Ⅰ)某学校开设了4门体育类选修课和4门艺术类选修课,学生需从这8门课中选修2门或3门课,并且每类选修课至少选修1门,则不同的选课方案共有_____种(用数字作答).
考点一 排列、组合
64
(2)当从8门课中选修3门时,
综上所述,不同的选课方案共有16+24+24=64(种).
(2)(2023·南昌模拟)中国灯笼又统称为灯彩,是一种古老的汉族传统工艺品.灯笼综合了绘画、剪纸、纸扎、刺缝等工艺,与中国人的生活息息相连.灯笼成了中国人喜庆的象征.经过历代灯彩艺人的继承和发展,形成了丰富多彩的品种和高超的工艺水平,从种类上主要有宫灯、纱灯、吊灯等类型,现将红木宫灯、檀木宫灯、楠木纱灯、花梨木纱灯、恭喜发财吊灯、吉祥如意吊灯各一个随机挂成一排,则有且仅有一种类型的灯笼相邻的概率为
√
设红木宫灯、檀木宫灯为a1,a2;楠木纱灯、花梨木纱灯为b1,b2;恭喜发财吊灯、吉祥如意吊灯为c1,c2.
先求仅a1a2相邻的种数,把a1a2看作一个元素,此时有五个位置可选,
故仅a1a2相邻共有N1+N2+N3=96(种)排法,
同理得仅b1b2相邻,仅c1c2相邻的情况,也都有96种排法,
跟踪训练1 (1)(2023·茂名模拟)从1,2,3,4,5中任选3个不同的数字组成一个三位数,则该三位数能被3整除的概率为
√
要使该三位数能被3整除,只需3个数字和能被3整除即可,
(2)(2023·齐齐哈尔模拟)中国古代儒家要求学生掌握六种基本才能(六艺):礼、乐、射、御、书、数.某校国学社团周末开展“六艺”课程讲座活动,一天连排六节,每艺一节,则“射”与“数”之间最多间隔一艺的不同排课方法种数为
A.432 B.486
C.504 D.540
√
典例2 (1)(2022·新高考全国Ⅰ) (x+y)8的展开式中x2y6的系数为_____(用数字作答).
考点二 二项式定理
-28
(2)(多选)已知(2-x)2 024=a0+a1x+a2x2+…+a2 024x2 024,则
A.a0=1
B.a1+a2+a3+…+a2 024=22 024
C.a2 018=
D.|a1|+|a2|+|a3|+…+|a2 024|=32 024-22 024
√
√
令x=0,得22 024=a0,故A错误;
令x=1,得(2-1)2 024=a0+a1+a2+…+a2 024,
即a0+a1+a2+a3+…+a2 024=1,
所以a1+a2+a3+…+a2 024=1-22 024,故B错误;
由(2-x)2 024的展开式的通项及题意,
得|a1|+|a2|+|a3|+…+|a2 024|=-a1+a2-a3+…+a2 024,
令x=-1,得a0-a1+a2-a3+…+a2 024=(2+1)2 024=32 024,
则-a1+a2-a3+…+a2 024=32 024-22 024,故D正确.
跟踪训练2 (1)(2023·汕头模拟)在 的展开式中,xy7的系数为
_______.
-720
(2)(多选)已知 (a>0)的展开式的各项系数之和为1 024,则展开
式中
A.奇数项的二项式系数和为256
B.第6项的系数最大
C.存在常数项
D.有理项共有6项
√
√
√
令x=1,得(a+1)10=1 024,则a=1或a=-3(舍去).
对于B,由题意知展开式共11项,第6项的系数最大,故B正确;
对于D,当r=0,2,4,6,8,10时,Tr+1为有理项,故有理项共有6项,故D正确.
典例3 (1)(多选)(2023·新高考全国Ⅱ)在信道内传输0,1信号,信号的传输相互独立.发送0时,收到1的概率为α(0<α<1),收到0的概率为1-α;发送1时,收到0的概率为β(0<β<1),收到1的概率为1-β.考虑两种传输方案:单次传输和三次传输.单次传输是指每个信号只发送1次;三次传输是指每个信号重复发送3次.收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1).
考点三 概率
A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为(1-
α)(1-β)2
B.采用三次传输方案,若发送1,则依次收到1,0,1的概率为β(1-β)2
C.采用三次传输方案,若发送1,则译码为1的概率为β(1-β)2+(1-β)3
D.当0<α<0.5时,若发送0,则采用三次传输方案译码为0的概率大于采用
单次传输方案译码为0的概率
√
√
√
对于A,依次发送1,0,1,则依次收到1,0,1的事件是发送1接收1、发送0接收0、发送1接收1这3个事件的积,
它们相互独立,所以所求概率为(1-β)(1-α)(1-β)=(1-α)(1-β)2,故A正确;
对于B,三次传输,发送1,相当于依次发送1,1,1,则依次收到1,0,1的事件是发送1接收1、发送1接收0、发送1接收1这3个事件的积,
它们相互独立,所以所求概率为(1-β)β(1-β)=β(1-β)2,故B正确;
对于C,三次传输,发送1,则译码为1的事件是依次收到1,1,0;1,0,1;0,1,1和1,1,1这4个事件的和,
对于D,三次传输,发送0,则译码为0的概率P=(1-α)2(1+2α),
单次传输发送0,则译码为0的概率P′=1-α,而0<α<0.5,
因此P-P′=(1-α)2(1+2α)-(1-α)=α(1-α)(1-2α)>0,即P>P′,故D正确.
(2)(2023·莆田模拟)某医用口罩生产厂家生产医用普通口罩、医用外科口罩、医用防护口罩三种产品,三种产品的生产比例如图所示,且三种产品中绑带式口罩的比例分别为90%,50%,40%.若从该厂生产的口罩中任选一个,则选到绑带式口罩的概率为
A.0.23 B.0.47
C.0.53 D.0.77
√
由题图可知医用普通口罩、医用外科口罩、医用防护口罩的占比分别为70%,20%,10%,
记事件A1,A2,A3分别表示选到医用普
通口罩、医用外科口罩、医用防护口罩,
则Ω=A1∪A2∪A3,且A1,A2,A3两两互斥,
所以P(A1)=0.7,P(A2)=0.2,P(A3)=0.1,
又三种产品中绑带式口罩的比例分别为90%,50%,40%,
记事件B为“选到绑带式口罩”,则P(B|A1)=0.9,P(B|A2)=0.5,P(B|A3)=0.4,
所以由全概率公式可得选到绑带式口罩
的概率为P(B)=0.7×0.9+0.2×0.5+0.1×0.4=0.77.
跟踪训练3 (1)(多选)(2023·益阳质检)给定事件A,B,C,且P(C)>0,则下列选项正确的是
A.P(A∪B|C)≤P(A|C)+P(B|C)
B.若P(A)>0,P(B)>0且A,B互斥,则A,B不可能相互独立
C.若P(A|C)+P(B|C)=1,则A,B互为对立事件
D.若P(ABC)=P(A)P(B)P(C),则A,B,C两两相互独立
√
√
对于A,①当A,B互斥时,P(A∪B|C)=P(A|C)+P(B|C),
②当A,B不互斥时,P(A∪B|C)对于B,若P(A)>0,P(B)>0且A,B互斥,那么P(AB)=0≠P(A)P(B),故A,B不可能相互独立,故B正确;
对于C,由P(A|C)+P(B|C)=1得在C事件发生的前提下A和B事件发生的概率为1,并不能得出A与B是对立事件,故C错误;
对于D,若P(ABC)=P(A)P(B)P(C),只能说明其中两个事件的积事件与另一事件相互独立,但推导不出三个事件两两相互独立,故D错误.
√
(2)(2023·广东大湾区联考)一堆苹果中大果数与小果数的比例为9∶1,现用一台水果分选机进行筛选.已知这台分选机把大果筛选为小果的概率为5%,把小果筛选为大果的概率为2%.经过一轮筛选后,现在从这台分选机筛选出来的“大果”里面随机抽取一个,则这个“大果”是真的大果的概率为
记事件A1为放入水果分选机的苹果为大果,事件A2为放入水果分选机的苹果为小果,
记事件B为水果分选机筛选的苹果为“大果”,
主要考查计数原理与概率,以选择题和填空题为主,其中要注意排列组合问题的求解方法与技巧,二项式(a+b)n的通项公式以及条件概率的求法和全概率公式的使用.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
1.(2023·湖南名校教研联盟)用红、黄、蓝三种颜色给下图着色,要求有公共边的两块不着同色.在所有着色方案中,①③⑤着色相同的有
A.96种 B.24种
C.48种 D.12种
√
2.(2023·全国甲卷)某地的中学生中有60%的同学爱好滑冰,50%的同学爱好滑雪,70%的同学爱好滑冰或爱好滑雪.在该地的中学生中随机调查一位同学,若该同学爱好滑雪,则该同学也爱好滑冰的概率为
A.0.8 B.0.6 C.0.5 D.0.4
√
1
2
3
4
5
6
7
8
9
10
11
12
方法一 如图,左圆表示爱好滑冰的学生所占比例,右圆表示爱好滑雪的学生所占比例,A表示爱好滑冰且不爱好滑雪的学生所占比例,B表示既爱好滑冰又爱好滑雪的学生所占比例,C表示爱好滑雪且不爱好滑冰的学生所占比例,
则0.6+0.5-B=0.7,
所以B=0.4,C=0.5-0.4=0.1.
1
2
3
4
5
6
7
8
9
10
11
12
方法二 令事件A,B分别表示该学生爱好滑冰、该学生爱好滑雪,
则P(A)=0.6,P(B)=0.5,P(AB)=P(A)+P(B)-0.7=0.4,
1
2
3
4
5
6
7
8
9
10
11
12
3.(2023·汕头模拟)现将A,B,C,D,E,F六个字母排成一排,若要求A,B相邻,且B,C不相邻,则不同的排列方式的种数为
A.192 B.240 C.120 D.28
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
4. 的展开式中常数项为
A.-6 B.-20 C.0 D.20
√
1
2
3
4
5
6
7
8
9
10
11
12
5.(2023·湖南新高考教学教研联盟联考)某高校计划在今年暑假安排编号为A,B,C,D,E,F的6名教师到4个不同的学校进行宣讲,每个学校至少安排1人,其中B,D必须安排在同一个学校.则不同的安排方法共有
A.96种 B.144种 C.240种 D.384种
√
1
2
3
4
5
6
7
8
9
10
11
12
6.(2023·岳阳模拟)某学校为落实“双减”政策,在课后服务时间开设了“球类”“棋类”“书法”“绘画”“舞蹈”五项活动.若甲同学准备从这五项活动中随机选三项,则“书法”和“绘画”这两项活动至多有一项被选中的概率为
A.0.9 B.0.7 C.0.6 D.0.3
√
1
2
3
4
5
6
7
8
9
10
11
12
“书法”和“绘画”这两项活动至多有一项被选中分两种情况:
7.(多选)已知(2-x)8=a0+a1x+a2x2+…+a8x8,则
A.a0=28
B.a1+a2+…+a8=1
C.|a1|+|a2|+|a3|+…+|a8|=38
D.a1+2a2+3a3+…+8a8=-8
√
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
取x=0,可得a0=28,故A正确;
取x=1,把a0=28代入可得a1+a2+…+a8=1-28,故B不正确;
取x=-1,可得|a1|+|a2|+|a3|+…+|a8|=-a1+a2-…+a8=38-28,故C不正确;
已知等式两边对x求导数可得-8(2-x)7=a1+2a2x+…+8a8x7,
取x=1,可得a1+2a2+3a3+…+8a8=-8,故D正确.
8.(多选)(2023·杭州模拟)一口袋中有除颜色外完全相同的3个红球和2个白球,从中无放回地随机取两次,每次取1个球,记事件A1为“第一次取出的是红球”;事件A2为“第一次取出的是白球”;事件B为“取出的两球同色”;事件C为“取出的两球中至少有一个红球”,则
A.事件A1,A2为互斥事件
B.事件B,C相互独立
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
第一次取出的球是红球还是白球两个事件不可能同时发生,它们是互斥的,故A正确;
由于红球有3个,白球有2个,事件B发生时,两球同为白色或同为红色,
1
2
3
4
5
6
7
8
9
10
11
12
则P(BC)≠P(B)P(C),所以事件B,C不相互独立,故B错误;
1
2
3
4
5
6
7
8
9
10
11
12
9.(2023·德阳质检)已知(1-ax)5(1+3x)4的展开式中x的系数为2,则实数a的值为_____.
2
1
2
3
4
5
6
7
8
9
10
11
12
解得a=2.
1
2
3
4
5
6
7
8
9
10
11
12
由题意可得,乙在第一局负的情况下获胜,则乙还需要胜四局比赛.
1
2
3
4
5
6
7
8
9
10
11
12
11.(2023·华南师大附中模拟)我们称n(n∈N*)元有序实数组(x1,x2,…,xn)为n维向量,|x1|+|x2|+…+|xn|为该向量的范数.已知n维向量a=(x1,x2,…,xn),其中xi∈{-1,0,1},i=1,2,…,n,记范数为奇数的a的个
数为An,则An=__________.(用含n的式子表示,n∈N*)
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
当n为偶数时,范数为奇数,则xi=0的个数为奇数,即0的个数为1,3,5,…,n-1,
1
2
3
4
5
6
7
8
9
10
11
12
当n为奇数时,范数为奇数,则xi=0的个数为偶数,即0的个数为0,2,4,6,…,n-1,
1
2
3
4
5
6
7
8
9
10
11
12
12.(2023·佛山模拟)有n个编号分别为1,2,…,n的盒子,第1个盒子中有2个白球、1个黑球,其余盒子中均为1个白球、1个黑球,现从第1个盒子中任取一球放入第2个盒子,再从第2个盒子中任取一球放入第3个盒
子,以此类推,则从第2个盒子中取到白球的概率是____,从第n个盒子
中取到白球的概率是___________.
记事件Ai表示从第i(i=1,2,…,n)个盒子里取出白球,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
专题五 概率与统计
微专题31
计数原理与概率
主要考查两个计数原理、排列、组合的简单应用,时常与概率相结合,以选择题、填空题为主.二项式定理主要考查通项公式、二项式系数等知识,近几年也与函数、不等式、数列交汇考查.概率重点考查古典概型、条件概率的基本应用.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)(2023·新高考全国Ⅰ)某学校开设了4门体育类选修课和4门艺术类选修课,学生需从这8门课中选修2门或3门课,并且每类选修课至少选修1门,则不同的选课方案共有_____种(用数字作答).
考点一 排列、组合
64
(2)当从8门课中选修3门时,
综上所述,不同的选课方案共有16+24+24=64(种).
(2)(2023·南昌模拟)中国灯笼又统称为灯彩,是一种古老的汉族传统工艺品.灯笼综合了绘画、剪纸、纸扎、刺缝等工艺,与中国人的生活息息相连.灯笼成了中国人喜庆的象征.经过历代灯彩艺人的继承和发展,形成了丰富多彩的品种和高超的工艺水平,从种类上主要有宫灯、纱灯、吊灯等类型,现将红木宫灯、檀木宫灯、楠木纱灯、花梨木纱灯、恭喜发财吊灯、吉祥如意吊灯各一个随机挂成一排,则有且仅有一种类型的灯笼相邻的概率为
√
设红木宫灯、檀木宫灯为a1,a2;楠木纱灯、花梨木纱灯为b1,b2;恭喜发财吊灯、吉祥如意吊灯为c1,c2.
先求仅a1a2相邻的种数,把a1a2看作一个元素,此时有五个位置可选,
故仅a1a2相邻共有N1+N2+N3=96(种)排法,
同理得仅b1b2相邻,仅c1c2相邻的情况,也都有96种排法,
跟踪训练1 (1)(2023·茂名模拟)从1,2,3,4,5中任选3个不同的数字组成一个三位数,则该三位数能被3整除的概率为
√
要使该三位数能被3整除,只需3个数字和能被3整除即可,
(2)(2023·齐齐哈尔模拟)中国古代儒家要求学生掌握六种基本才能(六艺):礼、乐、射、御、书、数.某校国学社团周末开展“六艺”课程讲座活动,一天连排六节,每艺一节,则“射”与“数”之间最多间隔一艺的不同排课方法种数为
A.432 B.486
C.504 D.540
√
典例2 (1)(2022·新高考全国Ⅰ) (x+y)8的展开式中x2y6的系数为_____(用数字作答).
考点二 二项式定理
-28
(2)(多选)已知(2-x)2 024=a0+a1x+a2x2+…+a2 024x2 024,则
A.a0=1
B.a1+a2+a3+…+a2 024=22 024
C.a2 018=
D.|a1|+|a2|+|a3|+…+|a2 024|=32 024-22 024
√
√
令x=0,得22 024=a0,故A错误;
令x=1,得(2-1)2 024=a0+a1+a2+…+a2 024,
即a0+a1+a2+a3+…+a2 024=1,
所以a1+a2+a3+…+a2 024=1-22 024,故B错误;
由(2-x)2 024的展开式的通项及题意,
得|a1|+|a2|+|a3|+…+|a2 024|=-a1+a2-a3+…+a2 024,
令x=-1,得a0-a1+a2-a3+…+a2 024=(2+1)2 024=32 024,
则-a1+a2-a3+…+a2 024=32 024-22 024,故D正确.
跟踪训练2 (1)(2023·汕头模拟)在 的展开式中,xy7的系数为
_______.
-720
(2)(多选)已知 (a>0)的展开式的各项系数之和为1 024,则展开
式中
A.奇数项的二项式系数和为256
B.第6项的系数最大
C.存在常数项
D.有理项共有6项
√
√
√
令x=1,得(a+1)10=1 024,则a=1或a=-3(舍去).
对于B,由题意知展开式共11项,第6项的系数最大,故B正确;
对于D,当r=0,2,4,6,8,10时,Tr+1为有理项,故有理项共有6项,故D正确.
典例3 (1)(多选)(2023·新高考全国Ⅱ)在信道内传输0,1信号,信号的传输相互独立.发送0时,收到1的概率为α(0<α<1),收到0的概率为1-α;发送1时,收到0的概率为β(0<β<1),收到1的概率为1-β.考虑两种传输方案:单次传输和三次传输.单次传输是指每个信号只发送1次;三次传输是指每个信号重复发送3次.收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1).
考点三 概率
A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为(1-
α)(1-β)2
B.采用三次传输方案,若发送1,则依次收到1,0,1的概率为β(1-β)2
C.采用三次传输方案,若发送1,则译码为1的概率为β(1-β)2+(1-β)3
D.当0<α<0.5时,若发送0,则采用三次传输方案译码为0的概率大于采用
单次传输方案译码为0的概率
√
√
√
对于A,依次发送1,0,1,则依次收到1,0,1的事件是发送1接收1、发送0接收0、发送1接收1这3个事件的积,
它们相互独立,所以所求概率为(1-β)(1-α)(1-β)=(1-α)(1-β)2,故A正确;
对于B,三次传输,发送1,相当于依次发送1,1,1,则依次收到1,0,1的事件是发送1接收1、发送1接收0、发送1接收1这3个事件的积,
它们相互独立,所以所求概率为(1-β)β(1-β)=β(1-β)2,故B正确;
对于C,三次传输,发送1,则译码为1的事件是依次收到1,1,0;1,0,1;0,1,1和1,1,1这4个事件的和,
对于D,三次传输,发送0,则译码为0的概率P=(1-α)2(1+2α),
单次传输发送0,则译码为0的概率P′=1-α,而0<α<0.5,
因此P-P′=(1-α)2(1+2α)-(1-α)=α(1-α)(1-2α)>0,即P>P′,故D正确.
(2)(2023·莆田模拟)某医用口罩生产厂家生产医用普通口罩、医用外科口罩、医用防护口罩三种产品,三种产品的生产比例如图所示,且三种产品中绑带式口罩的比例分别为90%,50%,40%.若从该厂生产的口罩中任选一个,则选到绑带式口罩的概率为
A.0.23 B.0.47
C.0.53 D.0.77
√
由题图可知医用普通口罩、医用外科口罩、医用防护口罩的占比分别为70%,20%,10%,
记事件A1,A2,A3分别表示选到医用普
通口罩、医用外科口罩、医用防护口罩,
则Ω=A1∪A2∪A3,且A1,A2,A3两两互斥,
所以P(A1)=0.7,P(A2)=0.2,P(A3)=0.1,
又三种产品中绑带式口罩的比例分别为90%,50%,40%,
记事件B为“选到绑带式口罩”,则P(B|A1)=0.9,P(B|A2)=0.5,P(B|A3)=0.4,
所以由全概率公式可得选到绑带式口罩
的概率为P(B)=0.7×0.9+0.2×0.5+0.1×0.4=0.77.
跟踪训练3 (1)(多选)(2023·益阳质检)给定事件A,B,C,且P(C)>0,则下列选项正确的是
A.P(A∪B|C)≤P(A|C)+P(B|C)
B.若P(A)>0,P(B)>0且A,B互斥,则A,B不可能相互独立
C.若P(A|C)+P(B|C)=1,则A,B互为对立事件
D.若P(ABC)=P(A)P(B)P(C),则A,B,C两两相互独立
√
√
对于A,①当A,B互斥时,P(A∪B|C)=P(A|C)+P(B|C),
②当A,B不互斥时,P(A∪B|C)
对于C,由P(A|C)+P(B|C)=1得在C事件发生的前提下A和B事件发生的概率为1,并不能得出A与B是对立事件,故C错误;
对于D,若P(ABC)=P(A)P(B)P(C),只能说明其中两个事件的积事件与另一事件相互独立,但推导不出三个事件两两相互独立,故D错误.
√
(2)(2023·广东大湾区联考)一堆苹果中大果数与小果数的比例为9∶1,现用一台水果分选机进行筛选.已知这台分选机把大果筛选为小果的概率为5%,把小果筛选为大果的概率为2%.经过一轮筛选后,现在从这台分选机筛选出来的“大果”里面随机抽取一个,则这个“大果”是真的大果的概率为
记事件A1为放入水果分选机的苹果为大果,事件A2为放入水果分选机的苹果为小果,
记事件B为水果分选机筛选的苹果为“大果”,
主要考查计数原理与概率,以选择题和填空题为主,其中要注意排列组合问题的求解方法与技巧,二项式(a+b)n的通项公式以及条件概率的求法和全概率公式的使用.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
1.(2023·湖南名校教研联盟)用红、黄、蓝三种颜色给下图着色,要求有公共边的两块不着同色.在所有着色方案中,①③⑤着色相同的有
A.96种 B.24种
C.48种 D.12种
√
2.(2023·全国甲卷)某地的中学生中有60%的同学爱好滑冰,50%的同学爱好滑雪,70%的同学爱好滑冰或爱好滑雪.在该地的中学生中随机调查一位同学,若该同学爱好滑雪,则该同学也爱好滑冰的概率为
A.0.8 B.0.6 C.0.5 D.0.4
√
1
2
3
4
5
6
7
8
9
10
11
12
方法一 如图,左圆表示爱好滑冰的学生所占比例,右圆表示爱好滑雪的学生所占比例,A表示爱好滑冰且不爱好滑雪的学生所占比例,B表示既爱好滑冰又爱好滑雪的学生所占比例,C表示爱好滑雪且不爱好滑冰的学生所占比例,
则0.6+0.5-B=0.7,
所以B=0.4,C=0.5-0.4=0.1.
1
2
3
4
5
6
7
8
9
10
11
12
方法二 令事件A,B分别表示该学生爱好滑冰、该学生爱好滑雪,
则P(A)=0.6,P(B)=0.5,P(AB)=P(A)+P(B)-0.7=0.4,
1
2
3
4
5
6
7
8
9
10
11
12
3.(2023·汕头模拟)现将A,B,C,D,E,F六个字母排成一排,若要求A,B相邻,且B,C不相邻,则不同的排列方式的种数为
A.192 B.240 C.120 D.28
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
4. 的展开式中常数项为
A.-6 B.-20 C.0 D.20
√
1
2
3
4
5
6
7
8
9
10
11
12
5.(2023·湖南新高考教学教研联盟联考)某高校计划在今年暑假安排编号为A,B,C,D,E,F的6名教师到4个不同的学校进行宣讲,每个学校至少安排1人,其中B,D必须安排在同一个学校.则不同的安排方法共有
A.96种 B.144种 C.240种 D.384种
√
1
2
3
4
5
6
7
8
9
10
11
12
6.(2023·岳阳模拟)某学校为落实“双减”政策,在课后服务时间开设了“球类”“棋类”“书法”“绘画”“舞蹈”五项活动.若甲同学准备从这五项活动中随机选三项,则“书法”和“绘画”这两项活动至多有一项被选中的概率为
A.0.9 B.0.7 C.0.6 D.0.3
√
1
2
3
4
5
6
7
8
9
10
11
12
“书法”和“绘画”这两项活动至多有一项被选中分两种情况:
7.(多选)已知(2-x)8=a0+a1x+a2x2+…+a8x8,则
A.a0=28
B.a1+a2+…+a8=1
C.|a1|+|a2|+|a3|+…+|a8|=38
D.a1+2a2+3a3+…+8a8=-8
√
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
取x=0,可得a0=28,故A正确;
取x=1,把a0=28代入可得a1+a2+…+a8=1-28,故B不正确;
取x=-1,可得|a1|+|a2|+|a3|+…+|a8|=-a1+a2-…+a8=38-28,故C不正确;
已知等式两边对x求导数可得-8(2-x)7=a1+2a2x+…+8a8x7,
取x=1,可得a1+2a2+3a3+…+8a8=-8,故D正确.
8.(多选)(2023·杭州模拟)一口袋中有除颜色外完全相同的3个红球和2个白球,从中无放回地随机取两次,每次取1个球,记事件A1为“第一次取出的是红球”;事件A2为“第一次取出的是白球”;事件B为“取出的两球同色”;事件C为“取出的两球中至少有一个红球”,则
A.事件A1,A2为互斥事件
B.事件B,C相互独立
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
第一次取出的球是红球还是白球两个事件不可能同时发生,它们是互斥的,故A正确;
由于红球有3个,白球有2个,事件B发生时,两球同为白色或同为红色,
1
2
3
4
5
6
7
8
9
10
11
12
则P(BC)≠P(B)P(C),所以事件B,C不相互独立,故B错误;
1
2
3
4
5
6
7
8
9
10
11
12
9.(2023·德阳质检)已知(1-ax)5(1+3x)4的展开式中x的系数为2,则实数a的值为_____.
2
1
2
3
4
5
6
7
8
9
10
11
12
解得a=2.
1
2
3
4
5
6
7
8
9
10
11
12
由题意可得,乙在第一局负的情况下获胜,则乙还需要胜四局比赛.
1
2
3
4
5
6
7
8
9
10
11
12
11.(2023·华南师大附中模拟)我们称n(n∈N*)元有序实数组(x1,x2,…,xn)为n维向量,|x1|+|x2|+…+|xn|为该向量的范数.已知n维向量a=(x1,x2,…,xn),其中xi∈{-1,0,1},i=1,2,…,n,记范数为奇数的a的个
数为An,则An=__________.(用含n的式子表示,n∈N*)
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
当n为偶数时,范数为奇数,则xi=0的个数为奇数,即0的个数为1,3,5,…,n-1,
1
2
3
4
5
6
7
8
9
10
11
12
当n为奇数时,范数为奇数,则xi=0的个数为偶数,即0的个数为0,2,4,6,…,n-1,
1
2
3
4
5
6
7
8
9
10
11
12
12.(2023·佛山模拟)有n个编号分别为1,2,…,n的盒子,第1个盒子中有2个白球、1个黑球,其余盒子中均为1个白球、1个黑球,现从第1个盒子中任取一球放入第2个盒子,再从第2个盒子中任取一球放入第3个盒
子,以此类推,则从第2个盒子中取到白球的概率是____,从第n个盒子
中取到白球的概率是___________.
记事件Ai表示从第i(i=1,2,…,n)个盒子里取出白球,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
同课章节目录
