高考数学专题四立体几何 微专题30 截面、交线问题 课件(共60张PPT)
文档属性
| 名称 | 高考数学专题四立体几何 微专题30 截面、交线问题 课件(共60张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览









文档简介
(共60张PPT)
专题四 立体几何
微专题30
截面、交线问题
“截面、交线”问题是高考立体几何问题最具创新意识的题型,它渗透了一些动态的线、面等元素,给静态的立体几何题赋予了活力.求截面、交线问题,一是与解三角形、多边形面积、扇形弧长等相结合求解,二是利用空间向量的坐标运算求解.
考情分析
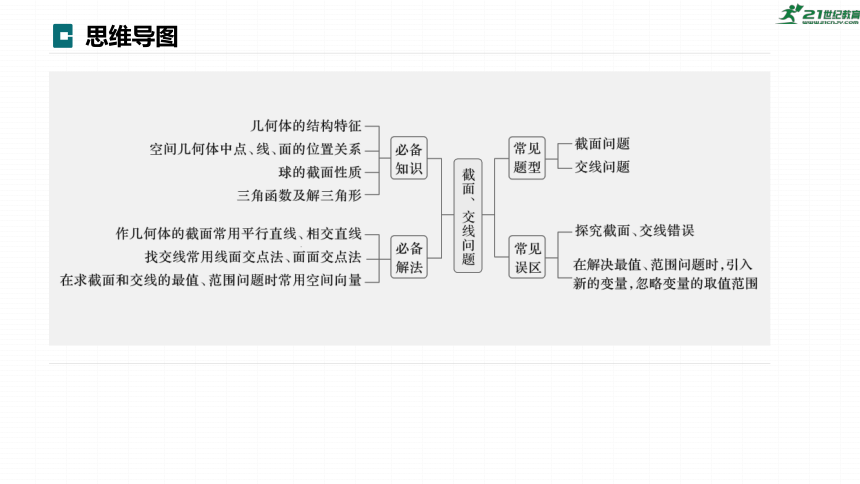
思维导图
内容索引
典型例题
热点突破
典例1 (1)在正方体ABCD-A1B1C1D1中,点Q是棱DD1上的动点,则过A,Q,B1三点的截面图形是
A.等边三角形 B.矩形
C.等腰梯形 D.以上都有可能
考点一 截面问题
√
当点Q与D1重合时,过A,Q,B1三点的截面是等边三角形AB1D1;
当点Q与D重合时,过A,Q,B1三点的截面是矩形AB1C1D;
当点Q与DD1的中点重合时,取C1D1的中点M,由于QM∥DC1,AB1∥DC1,所以QM∥AB1,
又AQ=MB1,故过A,Q,B1三点的截面是等腰梯
形AB1MQ,如图所示.
所以过A,Q,B1三点的截面图形可能是等边三角形、
矩形或等腰梯形.
(2)(2023·秦皇岛模拟)2023年12月7日为该年第21个节气“大雪”.“大雪”标志着仲冬时节正式开始,该节气的特点是气温显著下降,降水量增多,天气变得更加寒冷.“大雪”节气的民俗活动有打雪仗、赏雪景等.东北某学生小张滚了一个半径为2分米的雪球,准备对它进行切割,制作一个正六棱柱模型ABCDEF-A1B1C1D1E1F1,设M为B1E1的中点,当削去的雪最少时,平面ACM截该正六棱柱所得的截面面积为_____平方分米.
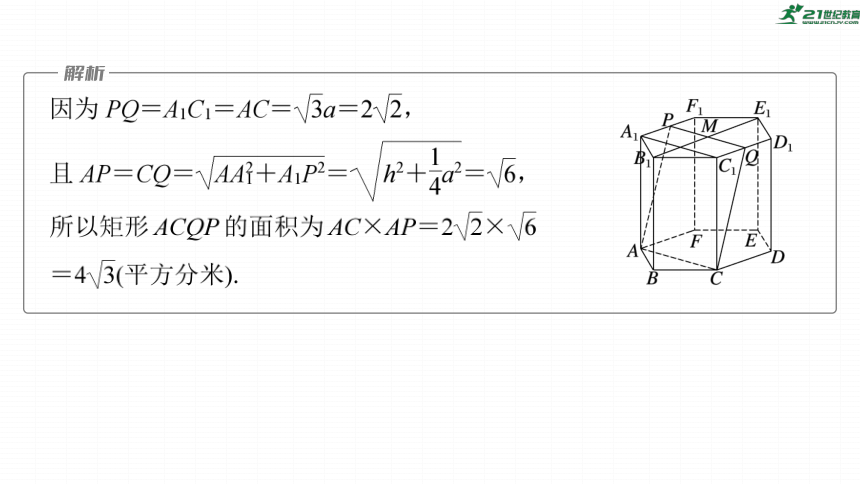
设正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为a,高为h.
若要使该正六棱柱的体积最大,正六棱柱应为球的内接正六棱柱中体积最大者,
如图,过M作PQ∥A1C1,交A1F1于点P,交C1D1于
点Q,则P,Q分别是A1F1,C1D1的中点,
又A1C1∥AC,所以PQ∥AC,易知四边形ACQP为矩形,
则矩形ACQP即为平面ACM截该正六棱柱所得的截面.
跟踪训练1 (1)(多选)已知正方体ABCD-A1B1C1D1,若AC1⊥平面α,则关于平面α截此正方体所得截面的判断正确的是
A.截面形状可能为正三角形
B.截面形状可能为正方形
C.截面形状可能为正六边形
D.截面形状可能为五边形
√
√
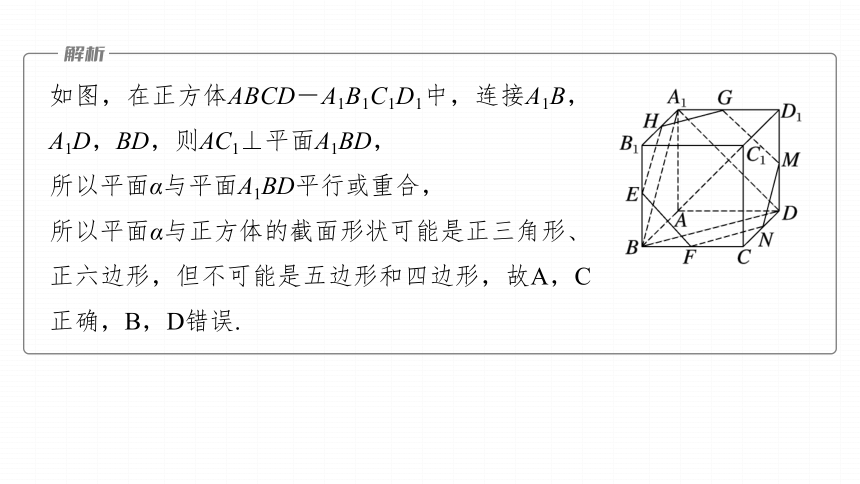
如图,在正方体ABCD-A1B1C1D1中,连接A1B,A1D,BD,则AC1⊥平面A1BD,
所以平面α与平面A1BD平行或重合,
所以平面α与正方体的截面形状可能是正三角形、正六边形,但不可能是五边形和四边形,故A,C正确,B,D错误.
(2)(2023·河北联考)如图,在直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠ACB=90°,AB=AA1=4,平面ABC1截三棱柱ABC-A1B1C1的外接球所得截面的面积为
√
由于△ABC为等腰直角三角形,所以△ABC的外心是AB的中点,设为O2,
设A1B1的中点为O1,连接O1O2,设O1O2的中点为O,
则O是直三棱柱ABC-A1B1C1的外接球的球心,
连接OC1,OA,OB,OA1,O1C1,如图所示,
设外接球的半径为R,
由于C1A1=C1B1,所以C1O1⊥A1B1,根据直棱柱的性质可知C1O1⊥AA1,
由于AA1∩A1B1=A1,AA1,A1B1 平面ABB1A1,
典例2 (1)(2023·茂名模拟)如图所示,正三棱锥P-ABC,底面边长为2,点P到平面ABC的距离为2,点M在平面PAC内,且点M到平面ABC的距离是点P到平面ABC距离的 过点M作一个平面,使其平行于直线PB和AC,则这个平面与三棱锥表面交线的总长为
考点二 交线问题
√
因为三棱锥P-ABC为正三棱锥,所以△ABC为等边三角形并且边长为2,
即AB=AC=BC=2.
又因为P-ABC为正三棱锥,如图,过点P作
底面ABC的垂线,垂足为O,连接AO,则点
O为△ABC的中心.
过点B作AC的垂线交AC于点H,连接PH.
在Rt△AHO中,
又因为PO=2,在Rt△AOP中,
因为三棱锥P-ABC为正三棱锥,因此△APC,
△APB,△BPC均为等腰三角形.
又点M到平面ABC的距离为点P到平面ABC距离的
过PH的三等分点(靠近点P)作Q1Q2∥AC交PC于点Q1,
交PA于点Q2,
则M位于线段Q1Q2上.
过点Q1作Q1Q4∥BP交BC于点Q4,过点Q4作Q3Q4∥AC交AB于点Q3,连接Q2Q3.
所以Q1Q2∥AC∥Q3Q4,则Q1,Q2,Q3,Q4四点共面.
因为Q1Q4∥BP,Q1Q4 平面Q1Q2Q3Q4,
BP 平面Q1Q2Q3Q4,
所以BP∥平面Q1Q2Q3Q4.
同理可得AC∥平面Q1Q2Q3Q4,
所以平面Q1Q2Q3Q4即为过点M且平行于直线PB和AC的平面.
(2)(多选)(2023·潍坊模拟)已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥平面ABCD,PA=AD=2,点M在平面ABCD上,且AM=λAD(0<λ<1),则
A.存在λ,使得直线PB与AM所成的角为
B.不存在λ,使得平面PAB⊥平面PBM
C.当λ为定值时,点P与点M轨迹上所有的点连线和平面ABCD围成的几何
体的外接球的表面积为4(λ2+1)2π
√
√
√
对于A,如图,
对于B,PA⊥平面ABCD,BC 平面ABCD,
所以BC⊥PA,又BC⊥AB,PA∩AB=A,PA,AB 平面PAB,
所以BC⊥平面PAB,所以点M要在直线BC上,
因为AM=λAD(0<λ<1),所以不存在λ,使得平面PAB⊥平面PBM,故B正确;
对于C,由题意知,几何体为圆锥,作圆锥及外接球的轴截面图,如图,
所以外接球的半径R满足R2=(2-R)2+(2λ)2,解得R=λ2+1,
所以外接球的表面积S=4(λ2+1)2π,故C正确;
将侧面展开,知球与侧面的交线为以点P为圆心, 为半径的圆与侧面展开图的交线,
设与AB交于点F,与AD交于点E,即图中 ,
又球与底面的交线是以点A为圆心, 为半径
的圆与底面ABCD的交线,
跟踪训练2 在正四棱锥P-ABCD中,已知PA=AB=2,O为底面ABCD的中心,以O为球心作一个半径为 的球,则该球的球面与侧面PCD的交线长度为
√
如图,取CD的中点E,则有OE⊥CD,PE⊥CD,
△PCD为正三角形,球心O在平面PCD上的投影M即
为△PCD的中心,
在Rt△OMF中,截面圆半径
所以∠FME=45°,
圆与三角形截得的三部分,由对称性可知,圆心角都
为90°,故该球的球面与侧面PCD的交线长度为截面圆周长的
总结提升
截面和交线问题在高考中一般为选择和填空题,难度较大.探究找截面一是几何法,常用直接连接、作平行线或作延长线找交点,找交线的方法常用线面交点法和面面交点法,二是利用空间向量法.
1.(2023·铅山一中模拟)将水平放置棱长为1的正方体容器(不计容器壁厚度)中注入一半的水,现将该正方体容器任意摆放,并保证水不溢出,则水面面积的最大值为
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图所示,
因为水的体积恰好是容器容积
的一半,
所以①水面可以是以 为边长
2.已知正方体ABCD-A1B1C1D1的棱长是2,E,F分别是棱B1C1和CC1的中点,点P在正方形BCC1B1(包括边界)内,当AP∥平面A1EF时,AP长度的最大值为a.以A为球心,a为半径的球面与底面A1B1C1D1的交线长为
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图所示,
分别取BB1,BC的中点M,N,连接MN,AM,AN,
所以EF∥MN,又MN 平面A1EF,EF 平面A1EF,
所以MN∥平面A1EF,
同理AN∥平面A1EF,又AN∩MN=N,
所以平面AMN∥平面A1EF,
因为点P在正方形BCC1B1(包括边界)内,且AP∥平面A1EF,
所以点P的轨迹是线段MN,
所以AP长度的最大值为
1
2
3
4
5
6
7
8
在平面A1B1C1D1内取一点G,使得A1G=1,
则AG=
所以以A为球心, 为半径的球面与底面A1B1C1D1
的交线为以A1为圆心,1为半径的 ,
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图,以CA,CC′所在直线分别为x轴、y轴建立平
面直角坐标系,则有C(0,0),O(1,0),
1
2
3
4
5
6
7
8
4.已知正方体ABCD-A1B1C1D1的棱长为4,E,F分别是棱AA1,BC的中点,则平面D1EF截该正方体所得的截面图形的周长为
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图,取CC1的中点G,连接BG,
则D1E∥BG,取CG的中点N,连接FN,
则FN∥BG,∴FN∥D1E,
则直线FN 平面D1EF,
延长D1E,DA交于点H,连接FH交AB于点M,
连接ME,则A为HD的中点,
则平面D1EF截该正方体所得的截面图形为D1EMFN,
由题意得A1E=AE=2,
则C1N=3,CN=1,
1
2
3
4
5
6
7
8
取AD的中点Q,连接QF,则AM∥FQ,
1
2
3
4
5
6
7
8
5.(多选)(2023·杭州模拟)如图,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,O2,O1分别为圆柱上、下底面的圆心,O为球心,EF为底面圆O1的一条直径,若球的半径r为2,则
A.球与圆柱的体积之比为2∶3
B.四面体CDEF体积的取值范围为(0,32]
C.平面DEF截得球的截面面积最小值为
D.若P为球面和圆柱侧面的交线上一点,则PE+PF
的取值范围为
1
2
3
4
5
6
7
8
√
√
1
2
3
4
5
6
7
8
对于A,球的体积V= 圆柱的体积V′=πr2×(2r)=16π,则球与圆柱的体积之比为2∶3,A正确;
对于B,设d为点E到平面BCD的距离,则01
2
3
4
5
6
7
8
对于C,如图,过点O作OH⊥DO1于点H,而O1O2
⊥DO2,则sin∠DO1O2=
1
2
3
4
5
6
7
8
对于D,令经过点P的圆柱的母线与下底面圆的公共点为Q,连接QE,QF,
当Q与E,F都不重合时,设∠QFE=θ,则QF=4cos θ,QE=4sin θ,当Q与E,F之一重合时,上式也成立,
1
2
3
4
5
6
7
8
即0≤sin 2θ≤1,
1
2
3
4
5
6
7
8
6.(多选)(2023·承德模拟)如图,正六棱柱ABCDEF-A1B1C1D1E1F1的各棱长均为1,下列选项正确的有
A.过A,C1,E1三点的平面α截该六棱柱的截
面面积为
B.过A,C1,E1三点的平面α将该六棱柱分割
成体积相等的两部分
C.以A为球心,1为半径的球面与该六棱柱的各面的交线总长为
D.以A为球心,2为半径的球面与该六棱柱的各面的交线总长为
√
√
√
1
2
3
4
5
6
7
8
对于A,过点A作GH∥C1E1,设GH∩BC=G,GH∩EF=H,
连接C1G,E1H,设C1G∩BB1=M,E1H∩FF1=N,连接AM,AN,
则过A,C1,E1三点的平面α截该六棱柱的截面即为AMC1E1N,
1
2
3
4
5
6
7
8
因为BB1⊥平面ABCDEF,GH 平面ABCDEF,
所以BB1⊥GH,
BC∩BB1=B,BC,BB1 平面BCC1B1,可得
GH⊥平面BCC1B1,C1G 平面BCC1B1,则GH⊥C1G,
由GH∥C1E1,则C1E1⊥C1G,
1
2
3
4
5
6
7
8
对于B,连接CE,B1F1,
因为BB1⊥平面ABCDEF,GB 平面ABCDEF,
所以BB1⊥GB,
BF⊥GB,BF∩BB1=B,BF,BB1 平面BFF1B1,
可得GB⊥平面BFF1B1,
则四棱锥A-BFNM的高为GB=
1
2
3
4
5
6
7
8
故平面α下半部分的体积V1=V四棱锥A-BFNM+
1
2
3
4
5
6
7
8
对于C,因为球的半径为1,则球只与侧面ABB1A1、侧面AFF1A1和底面ABCDEF相交,
对于D,因为球的半径为2,显然球不与侧面ABB1A1、侧面AFF1A1相交,
1
2
3
4
5
6
7
8
由选项A可知,GH⊥平面BCC1B1,即AG⊥平面BCC1B1,且
=2,
则球与侧面BCC1B1、侧面EFF1E1分别交于点C1,E1,
连接AC,则AC⊥CD,
因为CC1⊥平面ABCDEF,AC 平面ABCDEF,
所以CC1⊥AC,
又CD∩CC1=C,CD,CC1 平面CDD1C1,可得AC⊥平面CDD1C1,
1
2
3
4
5
6
7
8
同理可得,
又因为AA1⊥平面A1B1C1D1E1F1,且AA1=1,
又因为AD=2,则球与底面ABCDEF的交点为D,
口小肚大,代表着心胸开阔、和谐美满.如图,一个葫芦的果实可以近似看作两球相交所得的几何体Ω,其中Ω的下半部分是半径为3的球O1的一部分,Ω的上半部分是半径为 的球O2的一部分,且O1O2=6,则过直
线O1O2的平面截Ω所得截面的面积为___________.
1
2
3
4
5
6
7
8
7.(2023·湖北圆创联考)葫芦是一种爬藤植物,在我国传统文化中,其枝密集繁茂,象征着儿孙满堂、同气连枝;其音近于“福禄”,寓意着长寿多福、事业发达;其果
1
2
3
4
5
6
7
8
设N是两球面的一个公共点,且位于截面上,
8.(2023·江苏联考)在棱长为6的正四面体ABCD中,已知点O为该四面体的外接球的球心,则以O为球心, 为半径的球面与该四面体的表面形成的交线长为________.
1
2
3
4
5
6
7
8
如图1,取CD的中点M,△BCD的中心O1,
1
2
3
4
5
6
7
8
设球面与平面BCD形成的交线上的点为P,
如图2,设此圆与△BCD的边CD交于P1,P2,与边DB交于P3,P4,O1M⊥CD于点M,O1M1⊥BD于点M1,
1
2
3
4
5
6
7
8
同理∠P3O1M1=45°,
又∠MO1M1=120°,所以∠P2O1P3=30°,
所以球面与底面△BCD形成的交线是三段圆心角
为30°的圆弧, =
专题四 立体几何
微专题30
截面、交线问题
“截面、交线”问题是高考立体几何问题最具创新意识的题型,它渗透了一些动态的线、面等元素,给静态的立体几何题赋予了活力.求截面、交线问题,一是与解三角形、多边形面积、扇形弧长等相结合求解,二是利用空间向量的坐标运算求解.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)在正方体ABCD-A1B1C1D1中,点Q是棱DD1上的动点,则过A,Q,B1三点的截面图形是
A.等边三角形 B.矩形
C.等腰梯形 D.以上都有可能
考点一 截面问题
√
当点Q与D1重合时,过A,Q,B1三点的截面是等边三角形AB1D1;
当点Q与D重合时,过A,Q,B1三点的截面是矩形AB1C1D;
当点Q与DD1的中点重合时,取C1D1的中点M,由于QM∥DC1,AB1∥DC1,所以QM∥AB1,
又AQ=MB1,故过A,Q,B1三点的截面是等腰梯
形AB1MQ,如图所示.
所以过A,Q,B1三点的截面图形可能是等边三角形、
矩形或等腰梯形.
(2)(2023·秦皇岛模拟)2023年12月7日为该年第21个节气“大雪”.“大雪”标志着仲冬时节正式开始,该节气的特点是气温显著下降,降水量增多,天气变得更加寒冷.“大雪”节气的民俗活动有打雪仗、赏雪景等.东北某学生小张滚了一个半径为2分米的雪球,准备对它进行切割,制作一个正六棱柱模型ABCDEF-A1B1C1D1E1F1,设M为B1E1的中点,当削去的雪最少时,平面ACM截该正六棱柱所得的截面面积为_____平方分米.
设正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为a,高为h.
若要使该正六棱柱的体积最大,正六棱柱应为球的内接正六棱柱中体积最大者,
如图,过M作PQ∥A1C1,交A1F1于点P,交C1D1于
点Q,则P,Q分别是A1F1,C1D1的中点,
又A1C1∥AC,所以PQ∥AC,易知四边形ACQP为矩形,
则矩形ACQP即为平面ACM截该正六棱柱所得的截面.
跟踪训练1 (1)(多选)已知正方体ABCD-A1B1C1D1,若AC1⊥平面α,则关于平面α截此正方体所得截面的判断正确的是
A.截面形状可能为正三角形
B.截面形状可能为正方形
C.截面形状可能为正六边形
D.截面形状可能为五边形
√
√
如图,在正方体ABCD-A1B1C1D1中,连接A1B,A1D,BD,则AC1⊥平面A1BD,
所以平面α与平面A1BD平行或重合,
所以平面α与正方体的截面形状可能是正三角形、正六边形,但不可能是五边形和四边形,故A,C正确,B,D错误.
(2)(2023·河北联考)如图,在直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠ACB=90°,AB=AA1=4,平面ABC1截三棱柱ABC-A1B1C1的外接球所得截面的面积为
√
由于△ABC为等腰直角三角形,所以△ABC的外心是AB的中点,设为O2,
设A1B1的中点为O1,连接O1O2,设O1O2的中点为O,
则O是直三棱柱ABC-A1B1C1的外接球的球心,
连接OC1,OA,OB,OA1,O1C1,如图所示,
设外接球的半径为R,
由于C1A1=C1B1,所以C1O1⊥A1B1,根据直棱柱的性质可知C1O1⊥AA1,
由于AA1∩A1B1=A1,AA1,A1B1 平面ABB1A1,
典例2 (1)(2023·茂名模拟)如图所示,正三棱锥P-ABC,底面边长为2,点P到平面ABC的距离为2,点M在平面PAC内,且点M到平面ABC的距离是点P到平面ABC距离的 过点M作一个平面,使其平行于直线PB和AC,则这个平面与三棱锥表面交线的总长为
考点二 交线问题
√
因为三棱锥P-ABC为正三棱锥,所以△ABC为等边三角形并且边长为2,
即AB=AC=BC=2.
又因为P-ABC为正三棱锥,如图,过点P作
底面ABC的垂线,垂足为O,连接AO,则点
O为△ABC的中心.
过点B作AC的垂线交AC于点H,连接PH.
在Rt△AHO中,
又因为PO=2,在Rt△AOP中,
因为三棱锥P-ABC为正三棱锥,因此△APC,
△APB,△BPC均为等腰三角形.
又点M到平面ABC的距离为点P到平面ABC距离的
过PH的三等分点(靠近点P)作Q1Q2∥AC交PC于点Q1,
交PA于点Q2,
则M位于线段Q1Q2上.
过点Q1作Q1Q4∥BP交BC于点Q4,过点Q4作Q3Q4∥AC交AB于点Q3,连接Q2Q3.
所以Q1Q2∥AC∥Q3Q4,则Q1,Q2,Q3,Q4四点共面.
因为Q1Q4∥BP,Q1Q4 平面Q1Q2Q3Q4,
BP 平面Q1Q2Q3Q4,
所以BP∥平面Q1Q2Q3Q4.
同理可得AC∥平面Q1Q2Q3Q4,
所以平面Q1Q2Q3Q4即为过点M且平行于直线PB和AC的平面.
(2)(多选)(2023·潍坊模拟)已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥平面ABCD,PA=AD=2,点M在平面ABCD上,且AM=λAD(0<λ<1),则
A.存在λ,使得直线PB与AM所成的角为
B.不存在λ,使得平面PAB⊥平面PBM
C.当λ为定值时,点P与点M轨迹上所有的点连线和平面ABCD围成的几何
体的外接球的表面积为4(λ2+1)2π
√
√
√
对于A,如图,
对于B,PA⊥平面ABCD,BC 平面ABCD,
所以BC⊥PA,又BC⊥AB,PA∩AB=A,PA,AB 平面PAB,
所以BC⊥平面PAB,所以点M要在直线BC上,
因为AM=λAD(0<λ<1),所以不存在λ,使得平面PAB⊥平面PBM,故B正确;
对于C,由题意知,几何体为圆锥,作圆锥及外接球的轴截面图,如图,
所以外接球的半径R满足R2=(2-R)2+(2λ)2,解得R=λ2+1,
所以外接球的表面积S=4(λ2+1)2π,故C正确;
将侧面展开,知球与侧面的交线为以点P为圆心, 为半径的圆与侧面展开图的交线,
设与AB交于点F,与AD交于点E,即图中 ,
又球与底面的交线是以点A为圆心, 为半径
的圆与底面ABCD的交线,
跟踪训练2 在正四棱锥P-ABCD中,已知PA=AB=2,O为底面ABCD的中心,以O为球心作一个半径为 的球,则该球的球面与侧面PCD的交线长度为
√
如图,取CD的中点E,则有OE⊥CD,PE⊥CD,
△PCD为正三角形,球心O在平面PCD上的投影M即
为△PCD的中心,
在Rt△OMF中,截面圆半径
所以∠FME=45°,
圆与三角形截得的三部分,由对称性可知,圆心角都
为90°,故该球的球面与侧面PCD的交线长度为截面圆周长的
总结提升
截面和交线问题在高考中一般为选择和填空题,难度较大.探究找截面一是几何法,常用直接连接、作平行线或作延长线找交点,找交线的方法常用线面交点法和面面交点法,二是利用空间向量法.
1.(2023·铅山一中模拟)将水平放置棱长为1的正方体容器(不计容器壁厚度)中注入一半的水,现将该正方体容器任意摆放,并保证水不溢出,则水面面积的最大值为
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图所示,
因为水的体积恰好是容器容积
的一半,
所以①水面可以是以 为边长
2.已知正方体ABCD-A1B1C1D1的棱长是2,E,F分别是棱B1C1和CC1的中点,点P在正方形BCC1B1(包括边界)内,当AP∥平面A1EF时,AP长度的最大值为a.以A为球心,a为半径的球面与底面A1B1C1D1的交线长为
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图所示,
分别取BB1,BC的中点M,N,连接MN,AM,AN,
所以EF∥MN,又MN 平面A1EF,EF 平面A1EF,
所以MN∥平面A1EF,
同理AN∥平面A1EF,又AN∩MN=N,
所以平面AMN∥平面A1EF,
因为点P在正方形BCC1B1(包括边界)内,且AP∥平面A1EF,
所以点P的轨迹是线段MN,
所以AP长度的最大值为
1
2
3
4
5
6
7
8
在平面A1B1C1D1内取一点G,使得A1G=1,
则AG=
所以以A为球心, 为半径的球面与底面A1B1C1D1
的交线为以A1为圆心,1为半径的 ,
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图,以CA,CC′所在直线分别为x轴、y轴建立平
面直角坐标系,则有C(0,0),O(1,0),
1
2
3
4
5
6
7
8
4.已知正方体ABCD-A1B1C1D1的棱长为4,E,F分别是棱AA1,BC的中点,则平面D1EF截该正方体所得的截面图形的周长为
1
2
3
4
5
6
7
8
√
1
2
3
4
5
6
7
8
如图,取CC1的中点G,连接BG,
则D1E∥BG,取CG的中点N,连接FN,
则FN∥BG,∴FN∥D1E,
则直线FN 平面D1EF,
延长D1E,DA交于点H,连接FH交AB于点M,
连接ME,则A为HD的中点,
则平面D1EF截该正方体所得的截面图形为D1EMFN,
由题意得A1E=AE=2,
则C1N=3,CN=1,
1
2
3
4
5
6
7
8
取AD的中点Q,连接QF,则AM∥FQ,
1
2
3
4
5
6
7
8
5.(多选)(2023·杭州模拟)如图,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,O2,O1分别为圆柱上、下底面的圆心,O为球心,EF为底面圆O1的一条直径,若球的半径r为2,则
A.球与圆柱的体积之比为2∶3
B.四面体CDEF体积的取值范围为(0,32]
C.平面DEF截得球的截面面积最小值为
D.若P为球面和圆柱侧面的交线上一点,则PE+PF
的取值范围为
1
2
3
4
5
6
7
8
√
√
1
2
3
4
5
6
7
8
对于A,球的体积V= 圆柱的体积V′=πr2×(2r)=16π,则球与圆柱的体积之比为2∶3,A正确;
对于B,设d为点E到平面BCD的距离,则0
2
3
4
5
6
7
8
对于C,如图,过点O作OH⊥DO1于点H,而O1O2
⊥DO2,则sin∠DO1O2=
1
2
3
4
5
6
7
8
对于D,令经过点P的圆柱的母线与下底面圆的公共点为Q,连接QE,QF,
当Q与E,F都不重合时,设∠QFE=θ,则QF=4cos θ,QE=4sin θ,当Q与E,F之一重合时,上式也成立,
1
2
3
4
5
6
7
8
即0≤sin 2θ≤1,
1
2
3
4
5
6
7
8
6.(多选)(2023·承德模拟)如图,正六棱柱ABCDEF-A1B1C1D1E1F1的各棱长均为1,下列选项正确的有
A.过A,C1,E1三点的平面α截该六棱柱的截
面面积为
B.过A,C1,E1三点的平面α将该六棱柱分割
成体积相等的两部分
C.以A为球心,1为半径的球面与该六棱柱的各面的交线总长为
D.以A为球心,2为半径的球面与该六棱柱的各面的交线总长为
√
√
√
1
2
3
4
5
6
7
8
对于A,过点A作GH∥C1E1,设GH∩BC=G,GH∩EF=H,
连接C1G,E1H,设C1G∩BB1=M,E1H∩FF1=N,连接AM,AN,
则过A,C1,E1三点的平面α截该六棱柱的截面即为AMC1E1N,
1
2
3
4
5
6
7
8
因为BB1⊥平面ABCDEF,GH 平面ABCDEF,
所以BB1⊥GH,
BC∩BB1=B,BC,BB1 平面BCC1B1,可得
GH⊥平面BCC1B1,C1G 平面BCC1B1,则GH⊥C1G,
由GH∥C1E1,则C1E1⊥C1G,
1
2
3
4
5
6
7
8
对于B,连接CE,B1F1,
因为BB1⊥平面ABCDEF,GB 平面ABCDEF,
所以BB1⊥GB,
BF⊥GB,BF∩BB1=B,BF,BB1 平面BFF1B1,
可得GB⊥平面BFF1B1,
则四棱锥A-BFNM的高为GB=
1
2
3
4
5
6
7
8
故平面α下半部分的体积V1=V四棱锥A-BFNM+
1
2
3
4
5
6
7
8
对于C,因为球的半径为1,则球只与侧面ABB1A1、侧面AFF1A1和底面ABCDEF相交,
对于D,因为球的半径为2,显然球不与侧面ABB1A1、侧面AFF1A1相交,
1
2
3
4
5
6
7
8
由选项A可知,GH⊥平面BCC1B1,即AG⊥平面BCC1B1,且
=2,
则球与侧面BCC1B1、侧面EFF1E1分别交于点C1,E1,
连接AC,则AC⊥CD,
因为CC1⊥平面ABCDEF,AC 平面ABCDEF,
所以CC1⊥AC,
又CD∩CC1=C,CD,CC1 平面CDD1C1,可得AC⊥平面CDD1C1,
1
2
3
4
5
6
7
8
同理可得,
又因为AA1⊥平面A1B1C1D1E1F1,且AA1=1,
又因为AD=2,则球与底面ABCDEF的交点为D,
口小肚大,代表着心胸开阔、和谐美满.如图,一个葫芦的果实可以近似看作两球相交所得的几何体Ω,其中Ω的下半部分是半径为3的球O1的一部分,Ω的上半部分是半径为 的球O2的一部分,且O1O2=6,则过直
线O1O2的平面截Ω所得截面的面积为___________.
1
2
3
4
5
6
7
8
7.(2023·湖北圆创联考)葫芦是一种爬藤植物,在我国传统文化中,其枝密集繁茂,象征着儿孙满堂、同气连枝;其音近于“福禄”,寓意着长寿多福、事业发达;其果
1
2
3
4
5
6
7
8
设N是两球面的一个公共点,且位于截面上,
8.(2023·江苏联考)在棱长为6的正四面体ABCD中,已知点O为该四面体的外接球的球心,则以O为球心, 为半径的球面与该四面体的表面形成的交线长为________.
1
2
3
4
5
6
7
8
如图1,取CD的中点M,△BCD的中心O1,
1
2
3
4
5
6
7
8
设球面与平面BCD形成的交线上的点为P,
如图2,设此圆与△BCD的边CD交于P1,P2,与边DB交于P3,P4,O1M⊥CD于点M,O1M1⊥BD于点M1,
1
2
3
4
5
6
7
8
同理∠P3O1M1=45°,
又∠MO1M1=120°,所以∠P2O1P3=30°,
所以球面与底面△BCD形成的交线是三段圆心角
为30°的圆弧, =
同课章节目录
