高考数学专题五概率与统计 微专题33 统计与成对数据的统计分析 课件(共88张PPT)
文档属性
| 名称 | 高考数学专题五概率与统计 微专题33 统计与成对数据的统计分析 课件(共88张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览







文档简介
(共88张PPT)
微专题33
统计与成对数
据的统计分析
专题五 概率与统计
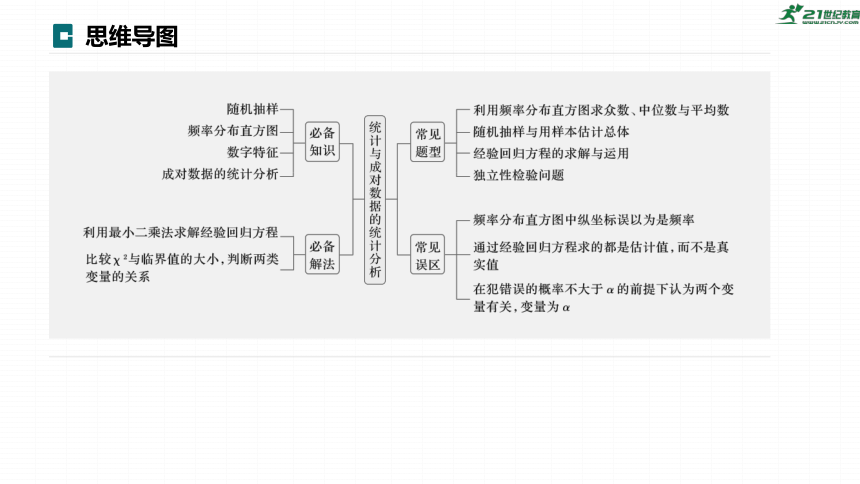
高考对本讲内容的考查往往以实际问题为背景,考查随机抽样与用样本估计总体、经验回归方程的求解与运用、独立性检验问题,常与概率综合考查,中等难度.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)(多选)(2023·南京模拟)新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车等.我国的新能源汽车发展开始于21世纪初,近年来发展迅速,连续8年产销量位居世界第一.
考点一 图表、数字特征
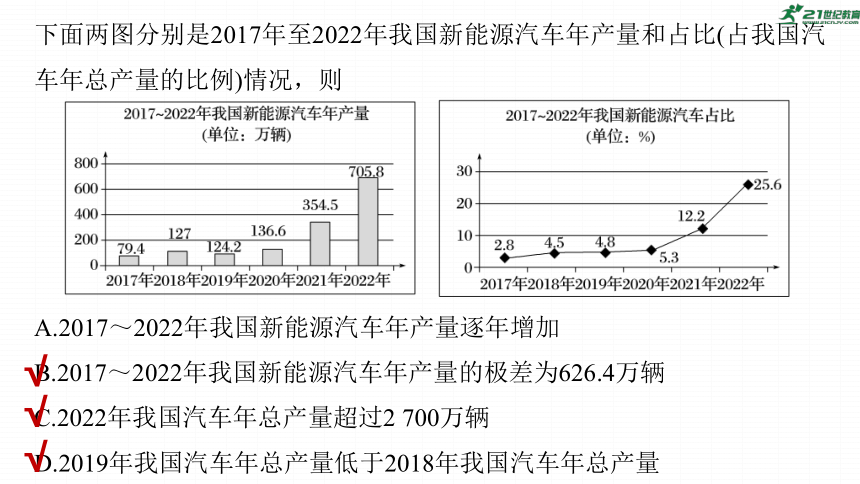
下面两图分别是2017年至2022年我国新能源汽车年产量和占比(占我国汽车年总产量的比例)情况,则
A.2017~2022年我国新能源汽车年产量逐年增加
B.2017~2022年我国新能源汽车年产量的极差为626.4万辆
C.2022年我国汽车年总产量超过2 700万辆
D.2019年我国汽车年总产量低于2018年我国汽车年总产量
√
√
√
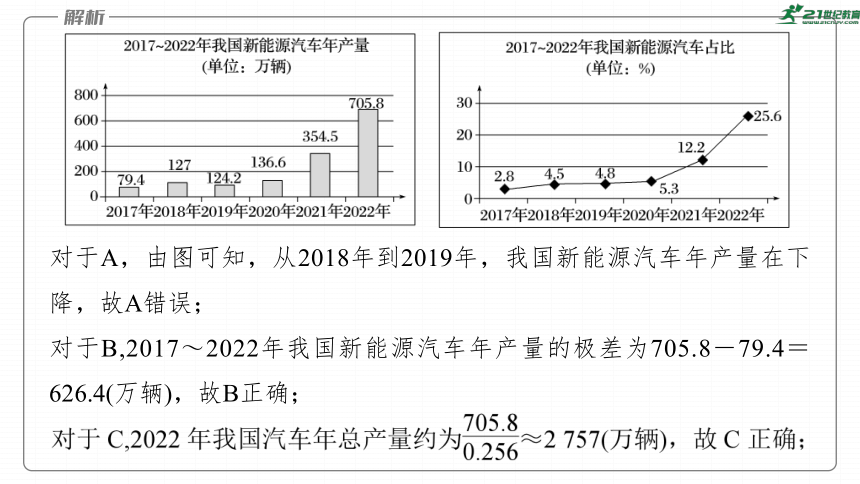
对于A,由图可知,从2018年到2019年,我国新能源汽车年产量在下降,故A错误;
对于B,2017~2022年我国新能源汽车年产量的极差为705.8-79.4=626.4(万辆),故B正确;
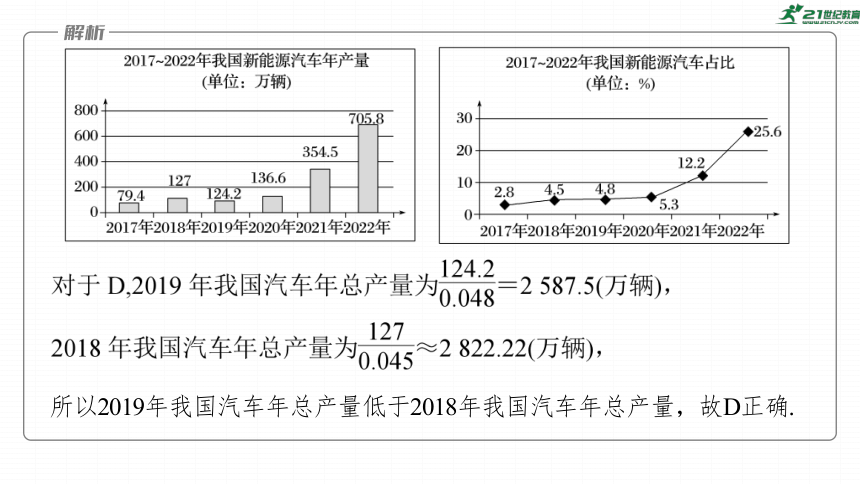
所以2019年我国汽车年总产量低于2018年我国汽车年总产量,故D正确.
(2)(多选)(2023·新高考全国Ⅰ)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
√
√
取x1=1,x2=x3=x4=x5=2,x6=9,
根据中位数的定义,将x1,x2,…,x6按从小到大的顺序进行排列,中位数是中间两个数的算术平均数,由于x1是最小值,x6是最大值,故x2,x3,x4,x5的中位数是将x2,x3,x4,x5按从小到大的顺序排列后中间两个数的算术平均数,与x1,x2,…,x6的中位数相等,故B正确;
根据极差的定义,知x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差,故D正确.
跟踪训练1 (1)(多选)(2023·菏泽模拟)在某次数学竞赛活动中,学生得分在 之间,满分100分,随机调查了200位学生的成绩,得到样本数据的频率分布直方图,则
A.图中x的值为0.029
B.参赛学生分数位于区间 上的概率
约为0.85
C.样本数据的75%分位数约为79
D.参赛学生的平均分数约为69.4
√
√
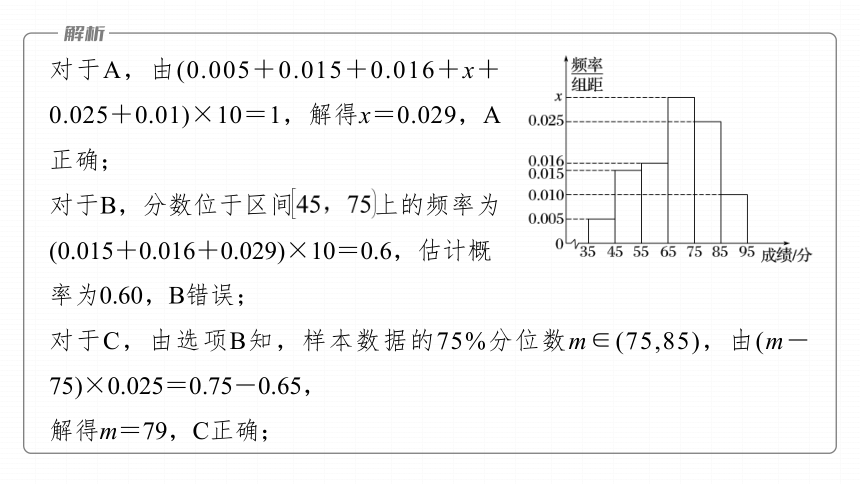
对于A,由(0.005+0.015+0.016+x+0.025+0.01)×10=1,解得x=0.029,A正确;
对于B,分数位于区间 上的频率为(0.015+0.016+0.029)×10=0.6,估计概
率为0.60,B错误;
对于C,由选项B知,样本数据的75%分位数m∈(75,85),由(m-75)×0.025=0.75-0.65,
解得m=79,C正确;
对于D,由频率分布直方图知,各小矩形面积从左到右依次为0.05,0.15,0.16,0.29,
0.25,0.1,
平均分数 =40×0.05+50×0.15+60×0.16+70×0.29+80×0.25+90×0.1=68.4,D错误.
(2)(多选)有一组样本甲的数据xi,一组样本乙的数据2xi+1,其中xi(i=1,2,3,4,5,6,7,8)为不完全相等的正数,则下列说法正确的是
A.样本甲的极差一定小于样本乙的极差
B.样本甲的方差一定大于样本乙的方差
C.若样本甲的中位数是m,则样本乙的中位数是2m+1
D.若样本甲的平均数是n,则样本乙的平均数是2n+1
√
√
√
不妨设样本甲的数据为0则样本乙的数据为2x1+1≤2x2+1≤…≤2x8+1,且2x1+1<2x8+1.
对于选项A,样本甲的极差为x8-x1>0,样本乙的极差为(2x8+1)-(2x1+1)=2(x8-x1),
因为2(x8-x1)-(x8-x1)=x8-x1>0,
即2(x8-x1)>x8-x1,
所以样本甲的极差一定小于样本乙的极差,故A正确;
所以样本甲的方差一定小于样本乙的方差,故B错误;
对于选项D,若样本甲的平均数是n,则样本乙的平均数是2n+1,故D正确.
典例2 (2023·辽阳模拟)2022年12月份以来,全国多个地区纷纷采取不同的形式发放多轮消费券,助力消费复苏.记发放的消费券额度为x(百万元),带动的消费为y(百万元).某省随机抽查的一些城市的数据如表所示.
考点二 回归分析
x 3 3 4 5 5 6 6 8
y 10 12 13 18 19 21 24 27
(1)根据表中的数据,请用样本相关系数说明y与x有很强的线性相关关系,并求出y关于x的经验回归方程;
(2)①若该省A城市在2023年2月份准备发放一轮额度为10百万元的消费券,利用(1)中求得的线性回归方程,预计可以带动多少消费?
当x=10时,=3.45×10+0.75=35.25,所以预计能带动的消费达35.25百万元.
②当实际值与估计值的差的绝对值与估计值的比值不超过10%时,认为发放的该轮消费券助力消费复苏是理想的.若该省A城市2023年2月份发放额度为10百万元的消费券后,经过一个月的统计,发现实际带动的消费为30百万元,请问发放的该轮消费券助力消费复苏是否理想?若不理想,请分析可能存在的原因.
因为 ≈15%>10%,所以发放的该轮消费券助力消费复苏不
是理想的.
发放消费券只是影响消费的其中一个因素,还有其他重要因素.
比如:A城市经济发展水平不高,居民的收入水平直接影响了居民的消费水平;
A城市人口数量有限、商品价格水平、消费者偏好、消费者年龄构成等因素一定程度上影响了消费总量.
跟踪训练2 (2023·承德模拟)某公司研制了一种对人畜无害的灭草剂,为了解其效果,通过实验,收集到其不同浓度x(mol/L)与灭死率y的数据,得下表:
浓度x (mol/L) 10-12 10-10 10-8 10-6 10-4
灭死率y 0.1 0.24 0.46 0.76 0.94
根据表格数据可知解释变量x呈指数增长,而响应变量y增长幅度不大,且相应的增加量大约相等,
浓度x (mol/L) 10-12 10-10 10-8 10-6 10-4
灭死率y 0.1 0.24 0.46 0.76 0.94
浓度x (mol/L) 10-12 10-10 10-8 10-6 10-4
灭死率y 0.1 0.24 0.46 0.76 0.94
(2)①根据(1)的选择结果及表中数据,求出所选经验回归方程;
所以可得如下数据:
u -12 -10 -8 -6 -4
y 0.1 0.24 0.46 0.76 0.94
u -12 -10 -8 -6 -4
y 0.1 0.24 0.46 0.76 0.94
②依据①中所求经验回归方程,要使灭死率不低于0.8,估计该灭草剂的浓度至少要达到多少mol/L
所以x≥ ,即要使灭死率不低于0.8,则该灭草剂的浓度至少要达
到 mol/L.
典例3 (2023·长春模拟)某学校号召学生参加“每天锻炼1小时”活动,为了了解学生参与活动的情况,随机调查了100名学生一个月(30天)完成锻炼活动的天数,制成如下频数分布表:
考点三 独立性检验
天数 [0,5) [5,10) [10,15) [15,20) [20,25) [25,30]
人数 4 15 33 31 11 6
(1)由频数分布表可以认为,学生参加体育锻炼天数X近似服从正态分布N(μ,σ2),其中μ近似为样本的平均数(每组数据取区间的中间值),且σ=6.1,若全校有3 000名学生,求参加“每天锻炼1小时”活动超过21天的人数(精确到1);
参考数据:若随机变量X服从正态分布N(μ,σ2),
则P(μ-σ≤X≤μ+σ)≈0.682 7;
P(μ-2σ≤X≤μ+2σ)≈0.954 5;
P(μ-3σ≤X≤μ+3σ)≈0.997 3.
由频数分布表知μ=
天数 [0,5) [5,10) [10,15) [15,20) [20,25) [25,30]
人数 4 15 33 31 11 6
=14.9,则X~N(14.9,6.12),
∵P(μ-σ≤X≤μ+σ)≈0.682 7,
∴3 000×0.158 65=475.95≈476,
∴参加“每天锻炼1小时”活动超过21天的人数约为476.
(2)调查数据表明,参加“每天锻炼1小时”活动的天数在[15,30]的学生中有30名男生,天数在[0,15)的学生中有20名男生,学校对当月参加“每天锻炼1小时”活动超过15天的学生授予“运动达人”称号.请填写下面列联表:
性别 活动天数 合计
[0,15) [15,30] 男生
女生
合计
并依据小概率值α=0.05的独立性检验,能否认为学生性别与获得“运动达人”称号有关联?如果有关联,请解释它们之间如何相互影响.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
由频数分布表知,锻炼活动的天数在[0,15)的人数为4+15+33=52,
∵参加“每天锻炼1小时”活动的天数在[0,15)的学生中有20名男生,
∴参加“每天锻炼1小时”活动的天数在[0,15)的学生中女生人数为52-20=32,
由频数分布表知,锻炼活动的天数在[15,30]的人数为31+11+6=48,
∵参加“每天锻炼1小时”活动的天数在[15,30]的学生中有30名男生,
∴参加“每天锻炼1小时”活动的天数在[15,30]的学生中女生人数为48-30=18.
天数 [0,5) [5,10) [10,15) [15,20) [20,25) [25,30]
人数 4 15 33 31 11 6
∴列联表为
性别 活动天数 合计
[0,15) [15,30] 男生 20 30 50
女生 32 18 50
合计 52 48 100
零假设为H0:学生性别与获得“运动达人”称号无关,
依据α=0.05的独立性检验,我们推断H0不成立,即可以认为学生性别与获得“运动达人”称号有关,而且此推断犯错误的概率不大于0.05.
跟踪训练3 (2023·福州模拟)国内某大学为了了解本校学生的运动状况,采用简单随机抽样的方法从全校学生中抽取2 000人,调查他们平均每天运动的时间(单位:小时),统计表明该校学生平均每天运动的时间范围是[0,3],记平均每天运动的时间不少于2小时的学生为“运动达人”,少于2小时的学生为“非运动达人”.整理分析数据得到下面的列联表:
性别 运动时间 合计
运动达人 非运动达人 男生 1 100 300 1 400
女生 400 200 600
合计 1 500 500 2 000
零假设为H0:运动时间与性别之间无关联.根据列联表中的数据,算得χ2≈31.746,根据小概率值α=0.001的χ2独立性检验,则认为运动时间与性别有关,此推断犯错误的概率不大于0.001.
(1)如果将表中所有数据都缩小为原来的 在相同的检验标准下,再用
独立性检验推断运动时间与性别之间的关联性,结论还一样吗?请用统计语言解释其中的原因;
性别 运动时间 合计
运动达人 非运动达人 男生 1 100 300 1 400
女生 400 200 600
合计 1 500 500 2 000
临界值表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
方法一 改变数据之后的列联表为
性别 运动时间 合计
运动达人 非运动达人 男生 110 30 140
女生 40 20 60
合计 150 50 200
方法二 调整后的
≈3.175<10.828=x0.001,
(2)采用按样本性别比例分配的分层随机抽样方法抽取20名同学,并统计每位同学的运动时间,统计数据为:男生运动时间的平均数为2.5,方差为1;女生运动时间的平均数为1.5,方差为0.5,求这20名同学运动时间的均值与方差.
性别 运动时间 合计
运动达人 非运动达人 男生 1 100 300 1 400
女生 400 200 600
合计 1 500 500 2 000
记样本方差为s2,则s2=
所以这20名同学运动时间的均值为2.2,方差为1.06.
总结提升
1.对于回归分析主要考查求经验回归方程(非线性经验回归方程)和对变量值预测,用最小二乘法来求解经验回归方程,对非线性经验回归方程选择恰当的拟合函数,作恰当的变换,将其转化为线性函数.
2.对变量的预测,若已知经验回归方程(方程中无参数),可以直接将数值代入求得特定要求下的预测值;若经验回归方程中有参数,则根据经验回归直线一定经过点 求出参数值,得到经验回归方程,进而完成预测.
1.(2023·桂林模拟)某学校组建了演讲、舞蹈、航模、合唱、机器人五个社团,全校3 000名学生每人都参加且只参加其中一个社团,校团委从这3 000名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图.
1
2
3
4
5
6
7
8
9
10
则选取的学生中参加机器人社团的学生人数为
A.50 B.75 C.100 D.125
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
由题意,本次调查的人数为50÷10%=500,
所以机器人所占的比例为1-10%-20%-15%-40%=15%,
所以选取的学生中参加机器人社团的学生人数为500×15%=75.
2.(2023·潍坊质检)甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(图1),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(图2)完好,则
A.甲的单场平均得分比乙低
B.乙的60%分位数为19
C.甲、乙的极差均为11
D.乙得分的中位数是16.5
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
对于B,由8×60%=4.8,故乙的60%分位数为17,故B错误;
对于C,甲的极差为28-9=19,乙的极差为20-9=11,故C错误;
3.(2023·杭州模拟)某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉D(10,2)后,下列说法正确的是
A.样本相关系数r变小
B.决定系数R2变小
C.残差平方和变大
D.解释变量x与响应变量y的相关性变强
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
对于B,决定系数R2越接近于1,模型的拟合效果越好,若去掉D(10,2)后,决定系数R2变大,故B错误;
从图中可以看出D(10,2)较其他点,偏离直线远,故去掉D(10,2)后,回归效果更好,
对于A,样本相关系数 越接近于1,模型的拟合效果越好,若去掉D(10,2)后,样本相关系数r变大,故A错误;
1
2
3
4
5
6
7
8
9
10
对于C,残差平方和越小,模型的拟合效果越好,若去掉D(10,2)后,残差平方和变小,故C错误;
对于D,若去掉D(10,2)后,解释变量x与响应变量y的相关性变强,且是正相关,故D正确.
1
2
3
4
5
6
7
8
9
10
4.(2023·杭州模拟)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据x1+k,x2+k,…,xn+k,k为非零常数.则下列说法不正确的是
A.两组样本数据的极差相同
B.两组样本数据的标准差相同
C.两组样本数据的方差相同
D.两组样本数据的平均数相同
√
1
2
3
4
5
6
7
8
9
10
对于A选项,不妨设x1≤x2≤…≤xn,则样本数据x1,x2,…,xn的极差为xn-x1,
对于样本数据x1+k,x2+k,…,xn+k(k为非零常数),
则x1+k≤x2+k≤…≤xn+k,
所以样本数据x1+k,x2+k,…,xn+k(k为非零常数)的极差为(xn+k)-(x1+k)=xn-x1,所以两组样本数据的极差相同,A正确;
1
2
3
4
5
6
7
8
9
10
所以两组样本数据的平均数不相同,D错误;
所以两组样本数据的方差相同,这两组数据的标准差也相同,B,C正确.
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·广州模拟)某校随机抽取了100名学生测量体重,经统计,这些学生的体重数据(单位:kg)全部介于45至70之间,将数据整理得到如图所示的频率分布直方图,则
A.频率分布直方图中a的值为0.07
B.这100名学生中体重低于60 kg的人数为60
C.据此可以估计该校学生体重的第78百分位
数约为62
D.据此可以估计该校学生体重的平均数约为62.5
√
√
1
2
3
4
5
6
7
8
9
10
对于A,因为5×(0.01+a+0.06+0.04+0.02)=1,解得a=0.07,故A正确;
对于B,(0.01+0.07+0.06)×5×100=70(人),故B错误;
对于C,因为0.01×5+0.07×5+0.06×5=0.7,
0.01×5+0.07×5+0.06×5+0.04×5=0.9,0.7<0.78<0.9,所以第78百分位数位于 之间,
1
2
3
4
5
6
7
8
9
10
设第78百分位数为x,则0.01×5+0.07×5+0.06×5+(x-60)×0.04=0.78,解得x=62,故C正确;
对于D,因为0.01×5×47.5+0.07×5×52.5+0.06×5×57.5+0.04×5×62.5+0.02×5
×67.5=57.25,
即估计该校学生体重的平均数约为57.25,故D错误.
据(x1,y1),(x2,y2),…,(xn,yn)(其中 绘制了如图
所示的散点图.小明选择了如下2个回归模型来拟合茶水温度y随时间x的变化情况,回归模型一:y=kx+b(k<0,x≥0);回归模型二:y=kax+b(k>0,01
2
3
4
5
6
7
8
9
10
6.(多选)(2023·华南师大附中模拟)中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.为了建立茶水温度y随时间x变化的回归模型,小明每隔1分钟测量一次茶水温度,得到若干组数
C.若选择回归模型二,利用最小二乘法求得y=kax+b的图象一定经过点
( , )
D.当x=5时,通过回归模型二计算得y=65.1,用温度计测得实际茶水温
度为65.2,则残差为-0.1
1
2
3
4
5
6
7
8
9
10
A.茶水温度与时间这两个变量负相关
B.由于水温开始降得快,后面降得慢,最后趋于
平缓,因此模型二能更好的拟合茶水温度随时
间的变化情况
√
√
1
2
3
4
5
6
7
8
9
10
由散点图可知随时间增加,温度逐渐降低,且变化趋势趋于平缓,故为负相关且模型二拟合效果更好,故A,B正确;
根据非线性回归模型的拟合方法,先令t=ax,则y=kt+b,此时拟合为一元线性回归模型,
残差为观测值减估计值,即为65.2-65.1=0.1,故D错误.
1
2
3
4
5
6
7
8
9
10
7.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,蟋蟀鸣叫的频率x(单位:次数/分钟)与气温y(单位:℃)有较强的线性相关关系.某同学在当地通过观测,得到如下数据,并利用最小二乘法建立了y关于x的经验回归方程
当蟋蟀每分钟鸣叫52次时,该地当时的气温预测值为___.
x(次数/分钟) 24 36 40 60
y(℃) 26 28.6 30 35.4
33
1
2
3
4
5
6
7
8
9
10
8.某学校有高中学生500人,其中男生320人,女生180人.为了获得全体高中生身高的信息,按照比例分配分层随机抽样原则抽取样本,男生样本量为32,女生样本量为18,通过计算得男生身高样本平均数为173.5 cm,方差为17,女生身高样本平均数为163.83 cm,方差为30.03,则所有数据的样本平均数为________ cm,方差为______.
1
2
3
4
5
6
7
8
9
10
170.02
43.24
9.(2023·滁州模拟)大气污染物PM2.5(大气中直径小于或等于2.5 μm的颗粒物)的浓度超过一定的限度会影响人的身体健康.为了研究PM2.5的浓度是否受到汽车流量等因素的影响,研究人员选择了20个社会经济发展水平相近的城市,在每个城市选择一个交通点建立监测点,统计每个监测点24 h内过往的汽车流量(单位:千辆),同时在低空相同的高度测定每个监测点空气中PM2.5的平均浓度(单位:μg/m3),得到的数据如下表:
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
城市编号 汽车流量 PM2.5浓度 城市编号 汽车流量 PM2.5浓度
1 1.30 66 11 1.82 135
2 1.44 76 12 1.43 99
3 0.78 21 13 0.92 35
4 1.65 170 14 1.44 58
5 1.75 156 15 1.10 29
6 1.75 120 16 1.84 140
7 1.20 72 17 1.11 43
8 1.51 120 18 1.65 69
9 1.20 100 19 1.53 87
10 1.47 129 20 0.91 45
(1)根据上表,若24 h内过往的汽车流量大于等于1 500辆属于车流量大,PM2.5大于等于75μg/m3属于空气污染.请结合表中的数据,依据小概率值α=0.05的独立性检验,能否认为车流量大小与空气污染有关联?
1
2
3
4
5
6
7
8
9
10
α 0.100 0.050 0.010
xα 2.706 3.841 6.635
1
2
3
4
5
6
7
8
9
10
由表格,可得如下列联表,
零假设为H0:车流量大小与空气污染无关,
车流量小 车流量大 合计
空气无污染 8 1 9
空气污染 4 7 11
合计 12 8 20
故依据小概率值α=0.05的独立性检验,我们推断H0不成立,即能认为车流量大小与空气污染有关联.
(2)设PM2.5浓度为y,汽车流量为x.根据这些数据建立PM2.5浓度关于汽车流量的线性回归模型,并求出对应的经验回归方程(系数精确到0.01).
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
根据以上数据绘制了散点图观察散点图,两个变量间关系考虑用反比例函数模型y=a+ 和指数函数模型y=cedx分别对两个变量的关系进行拟合.已求得用指数函数模型
拟合的非线性经验回归方程为 =48.376e-0.195x,ln y与x的样本相关系数r1=-0.929.
10.(2023·襄阳模拟)某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,经统计得到如下数据:
1
2
3
4
5
6
7
8
9
10
x 1 2 3 4 5 6 7 8
y 56.5 31 22.75 17.8 15.95 14.5 13 12.5
(1)用反比例函数模型求y关于x的非线性经验回归方程;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
(2)用样本相关系数判断上述两个模型哪一个拟合效果更好(精确到0.001),并用其估计产量为10千件时每件产品的非原料成本;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
所以产量为10千件时每件产品的非原料成本约为11元.
(3)根据企业长期研究表明,非原料成本y服从正态分布N(μ,σ2),用样本平均数 作为μ的估计值,用样本标准差s作为σ的估计值,若非原料成本y在(μ-σ,μ+σ)之外,说明该成本异常,并称落在(μ-σ,μ+σ)之外的成本为异样成本,此时需寻找出现异样成本的原因.利用估计值判断上述非原料成本数据是否需要寻找出现异样成本的原因?
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
所以非原料成本y服从正态分布N(23,13.92),
所以(μ-σ,μ+σ)=(23-13.9,23+13.9)=(9.1,36.9),
因为56.5在(μ-σ,μ+σ)之外,所以需要此非原料成本数据寻找出现异样成本的原因.
微专题33
统计与成对数
据的统计分析
专题五 概率与统计
高考对本讲内容的考查往往以实际问题为背景,考查随机抽样与用样本估计总体、经验回归方程的求解与运用、独立性检验问题,常与概率综合考查,中等难度.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)(多选)(2023·南京模拟)新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车等.我国的新能源汽车发展开始于21世纪初,近年来发展迅速,连续8年产销量位居世界第一.
考点一 图表、数字特征
下面两图分别是2017年至2022年我国新能源汽车年产量和占比(占我国汽车年总产量的比例)情况,则
A.2017~2022年我国新能源汽车年产量逐年增加
B.2017~2022年我国新能源汽车年产量的极差为626.4万辆
C.2022年我国汽车年总产量超过2 700万辆
D.2019年我国汽车年总产量低于2018年我国汽车年总产量
√
√
√
对于A,由图可知,从2018年到2019年,我国新能源汽车年产量在下降,故A错误;
对于B,2017~2022年我国新能源汽车年产量的极差为705.8-79.4=626.4(万辆),故B正确;
所以2019年我国汽车年总产量低于2018年我国汽车年总产量,故D正确.
(2)(多选)(2023·新高考全国Ⅰ)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
√
√
取x1=1,x2=x3=x4=x5=2,x6=9,
根据中位数的定义,将x1,x2,…,x6按从小到大的顺序进行排列,中位数是中间两个数的算术平均数,由于x1是最小值,x6是最大值,故x2,x3,x4,x5的中位数是将x2,x3,x4,x5按从小到大的顺序排列后中间两个数的算术平均数,与x1,x2,…,x6的中位数相等,故B正确;
根据极差的定义,知x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差,故D正确.
跟踪训练1 (1)(多选)(2023·菏泽模拟)在某次数学竞赛活动中,学生得分在 之间,满分100分,随机调查了200位学生的成绩,得到样本数据的频率分布直方图,则
A.图中x的值为0.029
B.参赛学生分数位于区间 上的概率
约为0.85
C.样本数据的75%分位数约为79
D.参赛学生的平均分数约为69.4
√
√
对于A,由(0.005+0.015+0.016+x+0.025+0.01)×10=1,解得x=0.029,A正确;
对于B,分数位于区间 上的频率为(0.015+0.016+0.029)×10=0.6,估计概
率为0.60,B错误;
对于C,由选项B知,样本数据的75%分位数m∈(75,85),由(m-75)×0.025=0.75-0.65,
解得m=79,C正确;
对于D,由频率分布直方图知,各小矩形面积从左到右依次为0.05,0.15,0.16,0.29,
0.25,0.1,
平均分数 =40×0.05+50×0.15+60×0.16+70×0.29+80×0.25+90×0.1=68.4,D错误.
(2)(多选)有一组样本甲的数据xi,一组样本乙的数据2xi+1,其中xi(i=1,2,3,4,5,6,7,8)为不完全相等的正数,则下列说法正确的是
A.样本甲的极差一定小于样本乙的极差
B.样本甲的方差一定大于样本乙的方差
C.若样本甲的中位数是m,则样本乙的中位数是2m+1
D.若样本甲的平均数是n,则样本乙的平均数是2n+1
√
√
√
不妨设样本甲的数据为0
对于选项A,样本甲的极差为x8-x1>0,样本乙的极差为(2x8+1)-(2x1+1)=2(x8-x1),
因为2(x8-x1)-(x8-x1)=x8-x1>0,
即2(x8-x1)>x8-x1,
所以样本甲的极差一定小于样本乙的极差,故A正确;
所以样本甲的方差一定小于样本乙的方差,故B错误;
对于选项D,若样本甲的平均数是n,则样本乙的平均数是2n+1,故D正确.
典例2 (2023·辽阳模拟)2022年12月份以来,全国多个地区纷纷采取不同的形式发放多轮消费券,助力消费复苏.记发放的消费券额度为x(百万元),带动的消费为y(百万元).某省随机抽查的一些城市的数据如表所示.
考点二 回归分析
x 3 3 4 5 5 6 6 8
y 10 12 13 18 19 21 24 27
(1)根据表中的数据,请用样本相关系数说明y与x有很强的线性相关关系,并求出y关于x的经验回归方程;
(2)①若该省A城市在2023年2月份准备发放一轮额度为10百万元的消费券,利用(1)中求得的线性回归方程,预计可以带动多少消费?
当x=10时,=3.45×10+0.75=35.25,所以预计能带动的消费达35.25百万元.
②当实际值与估计值的差的绝对值与估计值的比值不超过10%时,认为发放的该轮消费券助力消费复苏是理想的.若该省A城市2023年2月份发放额度为10百万元的消费券后,经过一个月的统计,发现实际带动的消费为30百万元,请问发放的该轮消费券助力消费复苏是否理想?若不理想,请分析可能存在的原因.
因为 ≈15%>10%,所以发放的该轮消费券助力消费复苏不
是理想的.
发放消费券只是影响消费的其中一个因素,还有其他重要因素.
比如:A城市经济发展水平不高,居民的收入水平直接影响了居民的消费水平;
A城市人口数量有限、商品价格水平、消费者偏好、消费者年龄构成等因素一定程度上影响了消费总量.
跟踪训练2 (2023·承德模拟)某公司研制了一种对人畜无害的灭草剂,为了解其效果,通过实验,收集到其不同浓度x(mol/L)与灭死率y的数据,得下表:
浓度x (mol/L) 10-12 10-10 10-8 10-6 10-4
灭死率y 0.1 0.24 0.46 0.76 0.94
根据表格数据可知解释变量x呈指数增长,而响应变量y增长幅度不大,且相应的增加量大约相等,
浓度x (mol/L) 10-12 10-10 10-8 10-6 10-4
灭死率y 0.1 0.24 0.46 0.76 0.94
浓度x (mol/L) 10-12 10-10 10-8 10-6 10-4
灭死率y 0.1 0.24 0.46 0.76 0.94
(2)①根据(1)的选择结果及表中数据,求出所选经验回归方程;
所以可得如下数据:
u -12 -10 -8 -6 -4
y 0.1 0.24 0.46 0.76 0.94
u -12 -10 -8 -6 -4
y 0.1 0.24 0.46 0.76 0.94
②依据①中所求经验回归方程,要使灭死率不低于0.8,估计该灭草剂的浓度至少要达到多少mol/L
所以x≥ ,即要使灭死率不低于0.8,则该灭草剂的浓度至少要达
到 mol/L.
典例3 (2023·长春模拟)某学校号召学生参加“每天锻炼1小时”活动,为了了解学生参与活动的情况,随机调查了100名学生一个月(30天)完成锻炼活动的天数,制成如下频数分布表:
考点三 独立性检验
天数 [0,5) [5,10) [10,15) [15,20) [20,25) [25,30]
人数 4 15 33 31 11 6
(1)由频数分布表可以认为,学生参加体育锻炼天数X近似服从正态分布N(μ,σ2),其中μ近似为样本的平均数(每组数据取区间的中间值),且σ=6.1,若全校有3 000名学生,求参加“每天锻炼1小时”活动超过21天的人数(精确到1);
参考数据:若随机变量X服从正态分布N(μ,σ2),
则P(μ-σ≤X≤μ+σ)≈0.682 7;
P(μ-2σ≤X≤μ+2σ)≈0.954 5;
P(μ-3σ≤X≤μ+3σ)≈0.997 3.
由频数分布表知μ=
天数 [0,5) [5,10) [10,15) [15,20) [20,25) [25,30]
人数 4 15 33 31 11 6
=14.9,则X~N(14.9,6.12),
∵P(μ-σ≤X≤μ+σ)≈0.682 7,
∴3 000×0.158 65=475.95≈476,
∴参加“每天锻炼1小时”活动超过21天的人数约为476.
(2)调查数据表明,参加“每天锻炼1小时”活动的天数在[15,30]的学生中有30名男生,天数在[0,15)的学生中有20名男生,学校对当月参加“每天锻炼1小时”活动超过15天的学生授予“运动达人”称号.请填写下面列联表:
性别 活动天数 合计
[0,15) [15,30] 男生
女生
合计
并依据小概率值α=0.05的独立性检验,能否认为学生性别与获得“运动达人”称号有关联?如果有关联,请解释它们之间如何相互影响.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
由频数分布表知,锻炼活动的天数在[0,15)的人数为4+15+33=52,
∵参加“每天锻炼1小时”活动的天数在[0,15)的学生中有20名男生,
∴参加“每天锻炼1小时”活动的天数在[0,15)的学生中女生人数为52-20=32,
由频数分布表知,锻炼活动的天数在[15,30]的人数为31+11+6=48,
∵参加“每天锻炼1小时”活动的天数在[15,30]的学生中有30名男生,
∴参加“每天锻炼1小时”活动的天数在[15,30]的学生中女生人数为48-30=18.
天数 [0,5) [5,10) [10,15) [15,20) [20,25) [25,30]
人数 4 15 33 31 11 6
∴列联表为
性别 活动天数 合计
[0,15) [15,30] 男生 20 30 50
女生 32 18 50
合计 52 48 100
零假设为H0:学生性别与获得“运动达人”称号无关,
依据α=0.05的独立性检验,我们推断H0不成立,即可以认为学生性别与获得“运动达人”称号有关,而且此推断犯错误的概率不大于0.05.
跟踪训练3 (2023·福州模拟)国内某大学为了了解本校学生的运动状况,采用简单随机抽样的方法从全校学生中抽取2 000人,调查他们平均每天运动的时间(单位:小时),统计表明该校学生平均每天运动的时间范围是[0,3],记平均每天运动的时间不少于2小时的学生为“运动达人”,少于2小时的学生为“非运动达人”.整理分析数据得到下面的列联表:
性别 运动时间 合计
运动达人 非运动达人 男生 1 100 300 1 400
女生 400 200 600
合计 1 500 500 2 000
零假设为H0:运动时间与性别之间无关联.根据列联表中的数据,算得χ2≈31.746,根据小概率值α=0.001的χ2独立性检验,则认为运动时间与性别有关,此推断犯错误的概率不大于0.001.
(1)如果将表中所有数据都缩小为原来的 在相同的检验标准下,再用
独立性检验推断运动时间与性别之间的关联性,结论还一样吗?请用统计语言解释其中的原因;
性别 运动时间 合计
运动达人 非运动达人 男生 1 100 300 1 400
女生 400 200 600
合计 1 500 500 2 000
临界值表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
方法一 改变数据之后的列联表为
性别 运动时间 合计
运动达人 非运动达人 男生 110 30 140
女生 40 20 60
合计 150 50 200
方法二 调整后的
≈3.175<10.828=x0.001,
(2)采用按样本性别比例分配的分层随机抽样方法抽取20名同学,并统计每位同学的运动时间,统计数据为:男生运动时间的平均数为2.5,方差为1;女生运动时间的平均数为1.5,方差为0.5,求这20名同学运动时间的均值与方差.
性别 运动时间 合计
运动达人 非运动达人 男生 1 100 300 1 400
女生 400 200 600
合计 1 500 500 2 000
记样本方差为s2,则s2=
所以这20名同学运动时间的均值为2.2,方差为1.06.
总结提升
1.对于回归分析主要考查求经验回归方程(非线性经验回归方程)和对变量值预测,用最小二乘法来求解经验回归方程,对非线性经验回归方程选择恰当的拟合函数,作恰当的变换,将其转化为线性函数.
2.对变量的预测,若已知经验回归方程(方程中无参数),可以直接将数值代入求得特定要求下的预测值;若经验回归方程中有参数,则根据经验回归直线一定经过点 求出参数值,得到经验回归方程,进而完成预测.
1.(2023·桂林模拟)某学校组建了演讲、舞蹈、航模、合唱、机器人五个社团,全校3 000名学生每人都参加且只参加其中一个社团,校团委从这3 000名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图.
1
2
3
4
5
6
7
8
9
10
则选取的学生中参加机器人社团的学生人数为
A.50 B.75 C.100 D.125
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
由题意,本次调查的人数为50÷10%=500,
所以机器人所占的比例为1-10%-20%-15%-40%=15%,
所以选取的学生中参加机器人社团的学生人数为500×15%=75.
2.(2023·潍坊质检)甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(图1),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(图2)完好,则
A.甲的单场平均得分比乙低
B.乙的60%分位数为19
C.甲、乙的极差均为11
D.乙得分的中位数是16.5
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
对于B,由8×60%=4.8,故乙的60%分位数为17,故B错误;
对于C,甲的极差为28-9=19,乙的极差为20-9=11,故C错误;
3.(2023·杭州模拟)某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉D(10,2)后,下列说法正确的是
A.样本相关系数r变小
B.决定系数R2变小
C.残差平方和变大
D.解释变量x与响应变量y的相关性变强
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
对于B,决定系数R2越接近于1,模型的拟合效果越好,若去掉D(10,2)后,决定系数R2变大,故B错误;
从图中可以看出D(10,2)较其他点,偏离直线远,故去掉D(10,2)后,回归效果更好,
对于A,样本相关系数 越接近于1,模型的拟合效果越好,若去掉D(10,2)后,样本相关系数r变大,故A错误;
1
2
3
4
5
6
7
8
9
10
对于C,残差平方和越小,模型的拟合效果越好,若去掉D(10,2)后,残差平方和变小,故C错误;
对于D,若去掉D(10,2)后,解释变量x与响应变量y的相关性变强,且是正相关,故D正确.
1
2
3
4
5
6
7
8
9
10
4.(2023·杭州模拟)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据x1+k,x2+k,…,xn+k,k为非零常数.则下列说法不正确的是
A.两组样本数据的极差相同
B.两组样本数据的标准差相同
C.两组样本数据的方差相同
D.两组样本数据的平均数相同
√
1
2
3
4
5
6
7
8
9
10
对于A选项,不妨设x1≤x2≤…≤xn,则样本数据x1,x2,…,xn的极差为xn-x1,
对于样本数据x1+k,x2+k,…,xn+k(k为非零常数),
则x1+k≤x2+k≤…≤xn+k,
所以样本数据x1+k,x2+k,…,xn+k(k为非零常数)的极差为(xn+k)-(x1+k)=xn-x1,所以两组样本数据的极差相同,A正确;
1
2
3
4
5
6
7
8
9
10
所以两组样本数据的平均数不相同,D错误;
所以两组样本数据的方差相同,这两组数据的标准差也相同,B,C正确.
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·广州模拟)某校随机抽取了100名学生测量体重,经统计,这些学生的体重数据(单位:kg)全部介于45至70之间,将数据整理得到如图所示的频率分布直方图,则
A.频率分布直方图中a的值为0.07
B.这100名学生中体重低于60 kg的人数为60
C.据此可以估计该校学生体重的第78百分位
数约为62
D.据此可以估计该校学生体重的平均数约为62.5
√
√
1
2
3
4
5
6
7
8
9
10
对于A,因为5×(0.01+a+0.06+0.04+0.02)=1,解得a=0.07,故A正确;
对于B,(0.01+0.07+0.06)×5×100=70(人),故B错误;
对于C,因为0.01×5+0.07×5+0.06×5=0.7,
0.01×5+0.07×5+0.06×5+0.04×5=0.9,0.7<0.78<0.9,所以第78百分位数位于 之间,
1
2
3
4
5
6
7
8
9
10
设第78百分位数为x,则0.01×5+0.07×5+0.06×5+(x-60)×0.04=0.78,解得x=62,故C正确;
对于D,因为0.01×5×47.5+0.07×5×52.5+0.06×5×57.5+0.04×5×62.5+0.02×5
×67.5=57.25,
即估计该校学生体重的平均数约为57.25,故D错误.
据(x1,y1),(x2,y2),…,(xn,yn)(其中 绘制了如图
所示的散点图.小明选择了如下2个回归模型来拟合茶水温度y随时间x的变化情况,回归模型一:y=kx+b(k<0,x≥0);回归模型二:y=kax+b(k>0,0
2
3
4
5
6
7
8
9
10
6.(多选)(2023·华南师大附中模拟)中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.为了建立茶水温度y随时间x变化的回归模型,小明每隔1分钟测量一次茶水温度,得到若干组数
C.若选择回归模型二,利用最小二乘法求得y=kax+b的图象一定经过点
( , )
D.当x=5时,通过回归模型二计算得y=65.1,用温度计测得实际茶水温
度为65.2,则残差为-0.1
1
2
3
4
5
6
7
8
9
10
A.茶水温度与时间这两个变量负相关
B.由于水温开始降得快,后面降得慢,最后趋于
平缓,因此模型二能更好的拟合茶水温度随时
间的变化情况
√
√
1
2
3
4
5
6
7
8
9
10
由散点图可知随时间增加,温度逐渐降低,且变化趋势趋于平缓,故为负相关且模型二拟合效果更好,故A,B正确;
根据非线性回归模型的拟合方法,先令t=ax,则y=kt+b,此时拟合为一元线性回归模型,
残差为观测值减估计值,即为65.2-65.1=0.1,故D错误.
1
2
3
4
5
6
7
8
9
10
7.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,蟋蟀鸣叫的频率x(单位:次数/分钟)与气温y(单位:℃)有较强的线性相关关系.某同学在当地通过观测,得到如下数据,并利用最小二乘法建立了y关于x的经验回归方程
当蟋蟀每分钟鸣叫52次时,该地当时的气温预测值为___.
x(次数/分钟) 24 36 40 60
y(℃) 26 28.6 30 35.4
33
1
2
3
4
5
6
7
8
9
10
8.某学校有高中学生500人,其中男生320人,女生180人.为了获得全体高中生身高的信息,按照比例分配分层随机抽样原则抽取样本,男生样本量为32,女生样本量为18,通过计算得男生身高样本平均数为173.5 cm,方差为17,女生身高样本平均数为163.83 cm,方差为30.03,则所有数据的样本平均数为________ cm,方差为______.
1
2
3
4
5
6
7
8
9
10
170.02
43.24
9.(2023·滁州模拟)大气污染物PM2.5(大气中直径小于或等于2.5 μm的颗粒物)的浓度超过一定的限度会影响人的身体健康.为了研究PM2.5的浓度是否受到汽车流量等因素的影响,研究人员选择了20个社会经济发展水平相近的城市,在每个城市选择一个交通点建立监测点,统计每个监测点24 h内过往的汽车流量(单位:千辆),同时在低空相同的高度测定每个监测点空气中PM2.5的平均浓度(单位:μg/m3),得到的数据如下表:
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
城市编号 汽车流量 PM2.5浓度 城市编号 汽车流量 PM2.5浓度
1 1.30 66 11 1.82 135
2 1.44 76 12 1.43 99
3 0.78 21 13 0.92 35
4 1.65 170 14 1.44 58
5 1.75 156 15 1.10 29
6 1.75 120 16 1.84 140
7 1.20 72 17 1.11 43
8 1.51 120 18 1.65 69
9 1.20 100 19 1.53 87
10 1.47 129 20 0.91 45
(1)根据上表,若24 h内过往的汽车流量大于等于1 500辆属于车流量大,PM2.5大于等于75μg/m3属于空气污染.请结合表中的数据,依据小概率值α=0.05的独立性检验,能否认为车流量大小与空气污染有关联?
1
2
3
4
5
6
7
8
9
10
α 0.100 0.050 0.010
xα 2.706 3.841 6.635
1
2
3
4
5
6
7
8
9
10
由表格,可得如下列联表,
零假设为H0:车流量大小与空气污染无关,
车流量小 车流量大 合计
空气无污染 8 1 9
空气污染 4 7 11
合计 12 8 20
故依据小概率值α=0.05的独立性检验,我们推断H0不成立,即能认为车流量大小与空气污染有关联.
(2)设PM2.5浓度为y,汽车流量为x.根据这些数据建立PM2.5浓度关于汽车流量的线性回归模型,并求出对应的经验回归方程(系数精确到0.01).
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
根据以上数据绘制了散点图观察散点图,两个变量间关系考虑用反比例函数模型y=a+ 和指数函数模型y=cedx分别对两个变量的关系进行拟合.已求得用指数函数模型
拟合的非线性经验回归方程为 =48.376e-0.195x,ln y与x的样本相关系数r1=-0.929.
10.(2023·襄阳模拟)某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,经统计得到如下数据:
1
2
3
4
5
6
7
8
9
10
x 1 2 3 4 5 6 7 8
y 56.5 31 22.75 17.8 15.95 14.5 13 12.5
(1)用反比例函数模型求y关于x的非线性经验回归方程;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
(2)用样本相关系数判断上述两个模型哪一个拟合效果更好(精确到0.001),并用其估计产量为10千件时每件产品的非原料成本;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
所以产量为10千件时每件产品的非原料成本约为11元.
(3)根据企业长期研究表明,非原料成本y服从正态分布N(μ,σ2),用样本平均数 作为μ的估计值,用样本标准差s作为σ的估计值,若非原料成本y在(μ-σ,μ+σ)之外,说明该成本异常,并称落在(μ-σ,μ+σ)之外的成本为异样成本,此时需寻找出现异样成本的原因.利用估计值判断上述非原料成本数据是否需要寻找出现异样成本的原因?
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
所以非原料成本y服从正态分布N(23,13.92),
所以(μ-σ,μ+σ)=(23-13.9,23+13.9)=(9.1,36.9),
因为56.5在(μ-σ,μ+σ)之外,所以需要此非原料成本数据寻找出现异样成本的原因.
同课章节目录
