7.3万有引力理论的成就 课件 (共24张PPT) —2023-2024学年人教版(2019)高中物理必修第二册
文档属性
| 名称 | 7.3万有引力理论的成就 课件 (共24张PPT) —2023-2024学年人教版(2019)高中物理必修第二册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 700.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
万有引力理论的成就
学习目标定位
1.掌握应用万有引力定律解决问题的基本思路
3.会根据条件计算天体的密度
2.掌握两种计算天体质量的方法
4.了解发现未知天体的基本思路
目录
一、“称量”地球的质量
二、计算天体的质量
三、发现未知天体
四、预言哈雷彗星回归
1、万有引力定律的内容是什么?
2、该定律的适用条件是什么?
3、比例系数G是怎样测量的?
复习回顾
一、“称量”地球的质量
阿基米德:“给我一个支点,我可以撬动地球”
那是否我们给他一个天平(杠杆)他就能测量地球的质量了呢?
No,地球的质量无法用天平测量
高中物理
问题一:
那么地球的质量酒精如何测量?为什么把卡文迪许测量万有引力常量G说成是“测量地球的质量”?
方法:若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的万有引力,即:
GM=gR2
黄金代换式
例1:设地面附近的重力加速度g=9.8 m/s2,地球半径R=6.4×106 m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量.
答案 ME=
忽略地球自转
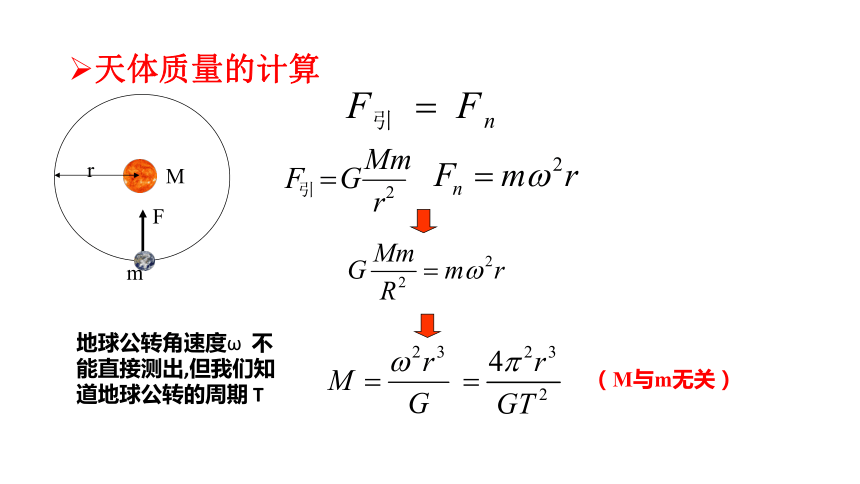
天体质量的计算
r
M
m
F
地球公转角速度ω 不能直接测出,但我们知道地球公转的周期 T
(M与m无关)
天体质量的计算
中心天体M
环绕天体m
求解思路:
环行天体的向心力由中心天体对其万有引力独家提供
具体方法:
注意:待求天体(M)的质量与环行天体(m)的质量无关
拓展:利用月球求地球质量
天体质量的计算
月球绕地球运行的周期T=27.3天,
月球与地球的平均距离r=3.84×108m
M地=5.98×1024kg
天体密度的计算
黄金替换
质量为m的物体在地球(星体)表面受到的万有引力等于其重力,即G=mg。可以得到:GM=gR2
由于G和M(地球质量)这两个参数往往不易记住,而g和R容易记住。所以粗略计算时,一般都采用上述代换,这就避开了万有引力常量G值和地球的质量M值
线速度v:
v=
角速度ω:
ω=
周期T:
向心加速度an:
三、发现未知天体
1、笔尖下发现的行星是哪一颗行星?
2、人们用类似的方法又发现了哪颗行星?
3、未知天体的发现有什么意义
1781年由英国物理学家威廉.赫歇尔发现了天王星,但人们观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差……
1:1845年英国人亚当斯和法国天文学家勒维耶各自独立用万有引力定律计算发现了“海王星”(第8个行星)。
2:1930年3月14日人们发现了从被称为太阳系第9个行星— 冥王星
3.1978年人们又发现了冥王星的卫星——卡戎
据我国航天专家介绍,自1957年10月4日前苏联发射世界上第一颗人造地球卫星以来(至2008.6),全世界发射的卫星总数已达5000余个,其中使用本国运载火箭发射本国制造的第一颗卫星的国家只有8个,按照卫星发射时间顺序为:前苏联、美国、法国、日本、中国、英国、印度和以色列。
资料库:
大利亚每日航天网2010年9月7日报道,欧洲咨询公司预测,未来十年全球将建造发射1220卫星。平均每年发射122颗卫星,这一数据比上一个十年年均发射77颗卫星的数据有显著提高,意味着政府管理者与商业运营商对卫星能力有更大的需求。
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
预言哈雷彗星回归
两
条
基
本
思
路
1、重力等于万有引力
2、万有引力提供向心力
课堂小结
应用万有引力定律计算天体运动的几个有关问题
1.解决天体问题的两条思路:
(1)万有引力提供向心力
(2)重力近似等于万有引力(m在M的表面附近,不考虑自转影响)
2.解决天体问题时应注意的问题
(1)在用万有引力等于向心力列式求天体的质量时,只能测出中心天体的质量,而环绕天体的质量在方程式中被消掉了.
(2)应用万有引力定律求解时还要注意挖掘题目中的隐含条件.如地球公转一周是365天,自转一周是24小时,其表面的重力加速度约为9.8 m/s2等.
(3)由 可以得到:GM=gR2.由于G和M(地球质量)这两个参数往往不易记住,而g和R容易记住.所以粗略计算时,一般都采用上述代换,这就避开了引力常量G值和地球的质量M值,方便多了.
万有引力理论的成就
学习目标定位
1.掌握应用万有引力定律解决问题的基本思路
3.会根据条件计算天体的密度
2.掌握两种计算天体质量的方法
4.了解发现未知天体的基本思路
目录
一、“称量”地球的质量
二、计算天体的质量
三、发现未知天体
四、预言哈雷彗星回归
1、万有引力定律的内容是什么?
2、该定律的适用条件是什么?
3、比例系数G是怎样测量的?
复习回顾
一、“称量”地球的质量
阿基米德:“给我一个支点,我可以撬动地球”
那是否我们给他一个天平(杠杆)他就能测量地球的质量了呢?
No,地球的质量无法用天平测量
高中物理
问题一:
那么地球的质量酒精如何测量?为什么把卡文迪许测量万有引力常量G说成是“测量地球的质量”?
方法:若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的万有引力,即:
GM=gR2
黄金代换式
例1:设地面附近的重力加速度g=9.8 m/s2,地球半径R=6.4×106 m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量.
答案 ME=
忽略地球自转
天体质量的计算
r
M
m
F
地球公转角速度ω 不能直接测出,但我们知道地球公转的周期 T
(M与m无关)
天体质量的计算
中心天体M
环绕天体m
求解思路:
环行天体的向心力由中心天体对其万有引力独家提供
具体方法:
注意:待求天体(M)的质量与环行天体(m)的质量无关
拓展:利用月球求地球质量
天体质量的计算
月球绕地球运行的周期T=27.3天,
月球与地球的平均距离r=3.84×108m
M地=5.98×1024kg
天体密度的计算
黄金替换
质量为m的物体在地球(星体)表面受到的万有引力等于其重力,即G=mg。可以得到:GM=gR2
由于G和M(地球质量)这两个参数往往不易记住,而g和R容易记住。所以粗略计算时,一般都采用上述代换,这就避开了万有引力常量G值和地球的质量M值
线速度v:
v=
角速度ω:
ω=
周期T:
向心加速度an:
三、发现未知天体
1、笔尖下发现的行星是哪一颗行星?
2、人们用类似的方法又发现了哪颗行星?
3、未知天体的发现有什么意义
1781年由英国物理学家威廉.赫歇尔发现了天王星,但人们观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差……
1:1845年英国人亚当斯和法国天文学家勒维耶各自独立用万有引力定律计算发现了“海王星”(第8个行星)。
2:1930年3月14日人们发现了从被称为太阳系第9个行星— 冥王星
3.1978年人们又发现了冥王星的卫星——卡戎
据我国航天专家介绍,自1957年10月4日前苏联发射世界上第一颗人造地球卫星以来(至2008.6),全世界发射的卫星总数已达5000余个,其中使用本国运载火箭发射本国制造的第一颗卫星的国家只有8个,按照卫星发射时间顺序为:前苏联、美国、法国、日本、中国、英国、印度和以色列。
资料库:
大利亚每日航天网2010年9月7日报道,欧洲咨询公司预测,未来十年全球将建造发射1220卫星。平均每年发射122颗卫星,这一数据比上一个十年年均发射77颗卫星的数据有显著提高,意味着政府管理者与商业运营商对卫星能力有更大的需求。
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
预言哈雷彗星回归
两
条
基
本
思
路
1、重力等于万有引力
2、万有引力提供向心力
课堂小结
应用万有引力定律计算天体运动的几个有关问题
1.解决天体问题的两条思路:
(1)万有引力提供向心力
(2)重力近似等于万有引力(m在M的表面附近,不考虑自转影响)
2.解决天体问题时应注意的问题
(1)在用万有引力等于向心力列式求天体的质量时,只能测出中心天体的质量,而环绕天体的质量在方程式中被消掉了.
(2)应用万有引力定律求解时还要注意挖掘题目中的隐含条件.如地球公转一周是365天,自转一周是24小时,其表面的重力加速度约为9.8 m/s2等.
(3)由 可以得到:GM=gR2.由于G和M(地球质量)这两个参数往往不易记住,而g和R容易记住.所以粗略计算时,一般都采用上述代换,这就避开了引力常量G值和地球的质量M值,方便多了.
