鲁教版(五四制)九年级数学下册第六章 对概率的进一步认识 专项测试试卷(含解析)
文档属性
| 名称 | 鲁教版(五四制)九年级数学下册第六章 对概率的进一步认识 专项测试试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 336.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 23:37:01 | ||
图片预览



文档简介
九年级数学下册第六章对概率的进一步认识专项测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、为解决“在甲、乙两个不透明口袋中随机摸球”的问题,小明画出如图1所示的树状图.已知这些球除颜色外无其他差别,根据树状图,小明从两个口袋中各随机取出一个球,其中取出的球是一个红球和一个白球的结果共有( )
A.种 B.种 C.种 D.种
2、从1,2,3中任取一个数作为十位上的数字,从4,5中任取一个数作为个位上的数字,组成的两位数是偶数的概率为( )
A. B. C. D.
3、为了深化落实“双减”工作,促进中小学生健康成长,教育部门加大了实地督查的力度,对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查,计划从“五项管理”中随机抽取两项进行问卷调查,则抽到“作业”和“手机”的概率为( )
A. B. C. D.
4、盒子中装有形状、大小完全相同的3个小球,球上分别标有数字﹣1,1,2,从中随机取出一个,其上的数字记为k1放回后再取一次,其上的数记为k2,则一次函数y=k1x+b与第一象限内y=的增减性一致的概率为( )
A. B. C. D.
5、一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了200次球,发现有140次摸到红球,由此估计这个口袋中红球的个数为( )
A.3个 B.4个 C.6个 D.7个
6、如图,有6张扑克牌,从中随机抽取一张,点数小于7的可能性大小是( )
A.3 B. C.1 D.
7、现有四张卡片依次写有“郑”“外”“加”“油”四个字(四张卡片除字不同外其他均相同),把四张卡片背面向上洗匀后,从中随机抽取两张,则抽到的汉字给好是“郑”和“外”的概率是( )
A. B. C. D.
8、一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,则估计红球的个数约为( )
A.35个 B.60个 C.70个 D.130个
9、连续抛掷两次骰子,它们的点都是奇数的概率是( )
A. B. C. D.
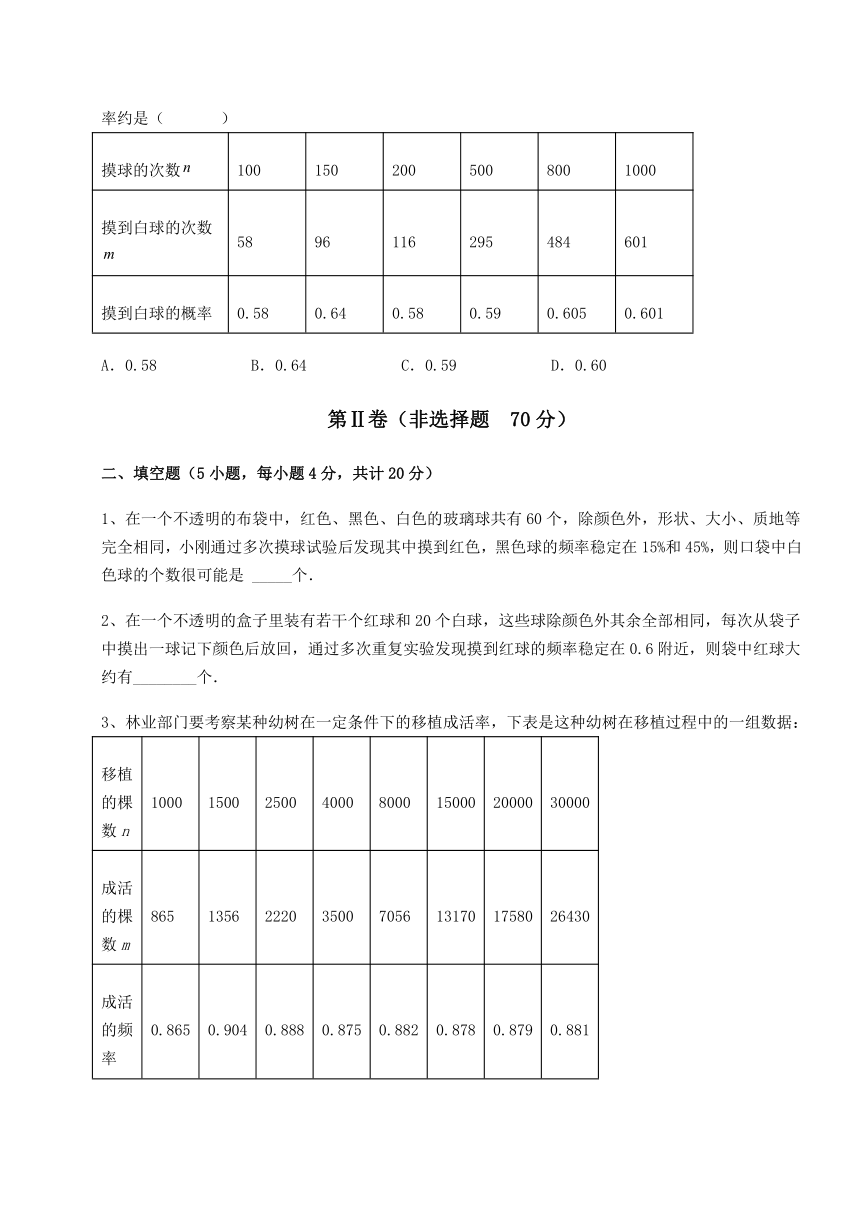
10、在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干只,某小组做摸球实验:将球搅匀后从中随机摸出一个,记下颜色,再放入袋中,不断重复,右表是活动中的一组数据,则摸到白球的概率约是( )
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 58 96 116 295 484 601
摸到白球的概率 0.58 0.64 0.58 0.59 0.605 0.601
A.0.58 B.0.64 C.0.59 D.0.60
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同,小刚通过多次摸球试验后发现其中摸到红色,黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 _____个.
2、在一个不透明的盒子里装有若干个红球和20个白球,这些球除颜色外其余全部相同,每次从袋子中摸出一球记下颜色后放回,通过多次重复实验发现摸到红球的频率稳定在0.6附近,则袋中红球大约有________个.
3、林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 865 1356 2220 3500 7056 13170 17580 26430
成活的频率 0.865 0.904 0.888 0.875 0.882 0.878 0.879 0.881
估计该种幼树在此条件下移植成活的概率为_______.
4、有6张除数字外无差别的卡片,上面分别写着1,2,3,4,5,6.随机抽取一张记作,放回并混合在一起,再随机抽一张记作,组成有序实数对,则点在直线上的概率为______
5、只有1和它本身两个因数且大于1的自然数叫做质数,我国数学家陈景润在有关质数的“哥德巴赫猜想”的研究中取得了世界领先的成果.从3,5,7,11,13,23这6个质数中随机抽取一个,则抽到个位数是3的可能性是________.
三、解答题(5小题,每小题10分,共计50分)
1、随着手机技术的迅猛发展,人们的沟通方式更便捷、多样.小强和他爸爸要在各自的手机里安装(微信、、钉钉)三种中的一种,用树状图或列表法求他俩选择同一种的概率.
2、为了继续宣传新冠疫苗接种的重要性,某小区物业部门准备在已经接种疫苗的居民中招募2名志愿宣传者,现有2名男性2名女性共4名居民报名.
(1)从4人中抽取1人为男性的概率是______;
(2)请用列表或画树状图的方法,求要从这4人中随机挑选2人,恰好抽到一名男性和一名女性的概率.
3、小颖为元旦联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果一个转盘转出了红色,另一个转盘转出了蓝色,那么游戏者获胜,因为红色和蓝色在一起配成了紫色.如果转盘的指针落在分割线上,则重新转动转盘.用列表或画树状图的方法,求游戏者获胜的概率.
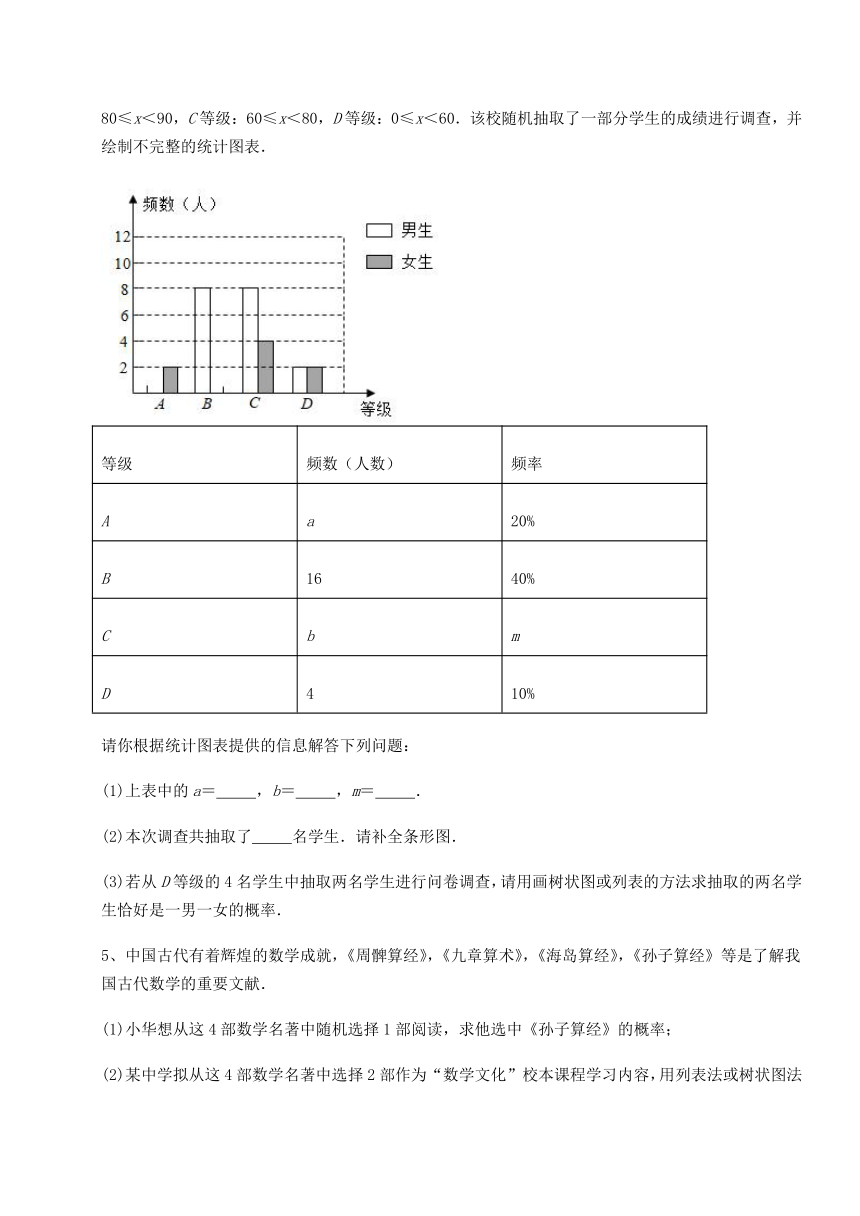
4、某校对八年级学生进行一次垃圾分类知识竞赛,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制不完整的统计图表.
等级 频数(人数) 频率
A a 20%
B 16 40%
C b m
D 4 10%
请你根据统计图表提供的信息解答下列问题:
(1)上表中的a= ,b= ,m= .
(2)本次调查共抽取了 名学生.请补全条形图.
(3)若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.
5、中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是了解我国古代数学的重要文献.
(1)小华想从这4部数学名著中随机选择1部阅读,求他选中《孙子算经》的概率;
(2)某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,用列表法或树状图法求出选中的2部名著中,其中1部是《周髀算经》的概率.
-参考答案-
一、单选题
1、B
【解析】
【分析】
根据树状图展示的所有结果,找出恰好一个红球和一个白球所占结果.
【详解】
由树状图得,从两个口袋中各随机取出一个球共有6种等可能结果,
其中恰好一个红球和一个白球有2种结果.
故选:B.
【点睛】
此题考查的是树状图的知识点,根据树状图展示的所有结果,找到符合条件的结果数是解题的关键.
2、A
【解析】
【分析】
根据题意列出树状图,进而问题可求解.
【详解】
解:由题意可得如下树状图:
∴组成的两位数是偶数的概率为;
故选A.
【点睛】
本题主要考查概率,熟练掌握利用树状图求解概率是解题的关键.
3、C
【解析】
【分析】
根据列表法或树状图法表示出来所有可能,然后找出满足条件的情况,即可得出概率.
【详解】
解:将作业、睡眠、手机、读物、体质“五项管理”简写为:业、睡、机、读、体,利用列表法可得:
业 睡 机 读 体
业 (业,睡) (业,机) (业,读) (业,体)
睡 (睡,业) (睡,机) (睡,读) (睡,体)
机 (机,业) (机,睡) (机,读) (机,体)
读 (读,业) (读,睡) (读,机) (读,体)
体 (体,业) (体,睡) (体,机) (体,读)
根据表格可得:共有20种可能,满足“作业”和“手机”的情况有两种,
∴ 抽到“作业”和“手机”的概率为:,
故选:C.
【点睛】
题目主要考查列表法或树状图法求概率,熟练掌握列表法或树状图法是解题关键.
4、B
【解析】
【分析】
分别计算所有情况数及满足条件的情况数,代入概率计算公式,可得答案.
【详解】
盒子中装有形状、大小完全相同的3个小球,球上分别标有数字-1,1,2,
从中随机取出一个,其上的数字记为,放回后再取一次,其上的数记为,
则共有9种情况,分别为:
(-1,-1),(-1,1),(-1,2),(1,-1),(1,1),(1,2),(2,-1),(2,1),(2,2),
一次函数y=k1x+b与第一象限内y=的增减性一致的有:
(-1,1),(-1,2),
一次函数y=k1x+b与第一象限内y=的增减性一致的概率为
故选B.
【点睛】
此题考查概率计算公式,判断一次函数与反比例函数的增减性,解题关键在于列出所有可能出现的情况.
5、D
【解析】
【分析】
估计利用频率估计概率可估计摸到红球的概率为0.7,然后根据概率公式计算这个口袋中红球的数量.
【详解】
解:因为共摸了200次球,发现有140次摸到红球,
所以估计摸到红球的概率为0.7,
所以估计这个口袋中红球的数量为10×0.7=7(个).
故选:D.
【点睛】
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
6、B
【解析】
【分析】
先用列举法得到所有的等可能的结果数,然后得到小于7的结果数,由此利用概率公式求解即可.
【详解】
解:由题意得:从这6张扑克牌,从中随机抽取一张,点数的可能为:3、4、5、7、8、10,一共6种结果,其中点数小于7的有3、4、5三种结果,
∴P点数小于7
故选B.
【点睛】
本题主要考查了用列举法求解概率,解题的关键在于能够熟练掌握用列举法求解概率.
7、C
【解析】
【分析】
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】
解:列表如下:
郑 外 加 油
郑 外,郑 加,郑 油,郑
外 郑,外 加,外 油,外
加 郑,加 外,加 油,加
油 郑,油 外,油 加,油
由表可知,共有12种等可能结果,其中抽到的汉字恰好是“郑”和“外”的有2种结果,
所以抽到的汉字恰好是“郑”和“外”的概率为.
故选:C.
【点睛】
本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.
8、C
【解析】
【分析】
根据大量重复试验后频率的稳定值即为概率,进行求解即可.
【详解】
解:∵一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,
∴红球的个数=200×35%=70个,
故选C.
【点睛】
本题主要考查了用频率估计概率,解题的关键在于能够熟练掌握大量重复试验下,频率的稳定值即为概率.
9、C
【解析】
【分析】
先列表,求解所有的等可能的结果数与符合条件的结果数,再利用概率公式进行计算即可.
【详解】
解:列表如下:
由表格信息可得:所有的等可能的结果数有个,符合条件的结果数有
故选C
【点睛】
本题考查的是利用列表法求解等可能事件的概率,掌握“列表法”是解本题的关键.
10、D
【解析】
【分析】
根据表格中的数据,随着实验次数的增大,频率逐渐稳定在0.60左右,即为摸出白球的概率.
【详解】
观察表格得:通过多次摸球实验后发现其中摸到白球的频率稳定在0.60左右,则摸到白球的概率约是0.60.
故选D
【点睛】
此题考查了利用频率估计概率,在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近.
二、填空题
1、24
【解析】
【分析】
在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,先求得白球的频率,再乘以总球数求解.
【详解】
解:小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在和,
口袋中白色球的个数很可能是个.
故答案为:24.
【点睛】
本题考查了利用用频率估计概率,解题的关键是要计算出口袋中白色球所占的比例,再计算其个数.
2、30
【解析】
【分析】
设袋中红球有x个,根据题意用红球数除以白球和红球的总数等于红球的频率列出方程即可求出红球数.
【详解】
解:设袋中红球有x个,根据题意,得:
,
解并检验得:x=30.
所以袋中红球有30个.
故答案为:30.
【点睛】
本题考查了利用频率估计概率,解决本题的关键是用频率的集中趋势来估计概率,这个固定的近似值
3、0.880
【解析】
【分析】
大量重复实验的情况下,当频率呈现一定的稳定性时,可以用这一稳定值估计事件发生的概率,据此可解.
【详解】
解:大量重复实验的情况下,当频率呈现一定的稳定性时,可以用这一稳定值估计事件发生的概率,
从上表可以看出,频率成活的频率,即稳定于0.880左右,
∴估计这种幼树移植成活率的概率约为0.88.
故答案为:0.880.
【点睛】
此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.
4、
【解析】
【分析】
画树状图表示所有等可能的结果,再计算点在直线上的概率.
【详解】
解:画树状图为:
共有36种机会均等的结果,其中组成有序实数对,则点在直线上的有4种,所以点在直线上的概率为,
故答案为:.
【点睛】
本题考查用树状图或列表法表示概率,是重要考点,难度较小,掌握相关知识是解题关键.
5、
【解析】
【分析】
先利用列举法求出个位数字是3的所有结果数,然后利用概率公式求解即可.
【详解】
解:从3,5,7,11,13,23这6个质数中随机抽取一个数一共有6种等可能性的结果数,其中抽到个位是3的有3,13,23三种结果数,
∴抽到个位数字是3的概率是,
故答案为:.
【点睛】
本题主要考查了概率的计算,熟练掌握列举法进行概率的计算是解决本题的关键.
三、解答题
1、他俩选择同一种的概率为.
【解析】
【分析】
列表得出所有结果,再由概率公式求解即可.
【详解】
解:根据题意列表如下:
共有9中等可能的结果,其中小强和爸爸选择同一种APP的情况有3种,
∴他俩选择同一种的概率为.
【点睛】
此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
2、 (1)
(2)
【解析】
【分析】
(1)找出从4人中抽取1人的等可能情况,再找出其中抽取1人为男性的情况,利用概率公式计算即可;
(2)列表或画树状图,列出所有等可能的结果,从中找出满足条件的等可能结果,再利用概率公式计算即可.
(1)
解:∵从4人中抽取1人的等可能情况有4种,其中抽取1人为男性的情况有2种,
∴从4人中抽取1人为男性的概率是,
故答案为;
(2)
解:由题可列下表:
由表可知,共有12种等可能的结果,而两个人选中一名男性和一名女性的结果有8种,
∴.
【点睛】
本题考查列举法求概率和列表或画树状图求概率,掌握列举法求概率的方法和列表或画树状图求概率方法与步骤,关键是从中找出满足条件的等可能结果,熟悉概率公式.
3、
【解析】
【分析】
先画出树状图,从而可得游戏的所有等可能的结果,再找出游戏者获胜的结果,然后利用概率公式进行计算即可得.
【详解】
解:设红色、蓝色和黄色分别用表示,画出树状图如下所示:
则这个游戏的所有等可能的结果共有6种,其中,游戏者获胜的结果有2种,
所以游戏者获胜的概率为,
答:游戏者获胜的概率为.
【点睛】
本题考查了利用列举法求概率,正确画出树状图是解题关键.
4、 (1)8,12,30%
(2)40,见解析
(3)
【解析】
【分析】
(1)根据D等级的人数和所占百分比列式计算求出本次调查共抽取的学生人数,即可解决问题;
(2)由(1)的结果求解即可;
(3)画树状图,共有12种等可能的结果,其中抽取的两名学生恰好是一男一女的结果有8种,再由概率公式求解即可.
(1)
解:本次调查共抽取的学生人数为:4÷10%=40(人),
∴a=40×20%=8,b=8+4=12,m=1﹣20%﹣40%﹣10%=30%;
故答案为:8,12,30%;
(2)
解:由(1)得:本次调查共抽取了40名学生,
故答案为:40,
补全条形图如图所示:
(3)
解:画树状图如图:
共有12种等可能的结果,其中抽取的两名学生恰好是一男一女的结果有8种,
∴抽取的两名学生恰好是一男一女的概率为=.
【点睛】
此题考查了树状图法与列表法求概率的知识以及直方图与统计表的知识.用到的知识点为:概率=所求情况数与总情况数之比.
5、 (1)他选中《孙子算经》的概率为
(2)其中1部是《周髀算经》的概率为
【解析】
(1)
小华想从这4部数学名著中随机选择1部阅读,
则他选中《孙子算经》的概率为.
(2)
将四部名著《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》分别记为A,B,C,D,
记其中1部是《周髀算经》为事件M.
用列表法列举出从4部名著中选择2部所能产生的全部结果:
第1部 第2部 A B C D
A
B
C
D
由表中可以看出,所有可能的结果有12种,并且它们出现的可能性相等.
其中事件M的结果有6种,即BA,CA,DA,AB,AC,AD,
.
【点睛】
本题考查了公式法求简单概率,列表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.熟练掌握求概率的方法是解题的关键.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、为解决“在甲、乙两个不透明口袋中随机摸球”的问题,小明画出如图1所示的树状图.已知这些球除颜色外无其他差别,根据树状图,小明从两个口袋中各随机取出一个球,其中取出的球是一个红球和一个白球的结果共有( )
A.种 B.种 C.种 D.种
2、从1,2,3中任取一个数作为十位上的数字,从4,5中任取一个数作为个位上的数字,组成的两位数是偶数的概率为( )
A. B. C. D.
3、为了深化落实“双减”工作,促进中小学生健康成长,教育部门加大了实地督查的力度,对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查,计划从“五项管理”中随机抽取两项进行问卷调查,则抽到“作业”和“手机”的概率为( )
A. B. C. D.
4、盒子中装有形状、大小完全相同的3个小球,球上分别标有数字﹣1,1,2,从中随机取出一个,其上的数字记为k1放回后再取一次,其上的数记为k2,则一次函数y=k1x+b与第一象限内y=的增减性一致的概率为( )
A. B. C. D.
5、一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了200次球,发现有140次摸到红球,由此估计这个口袋中红球的个数为( )
A.3个 B.4个 C.6个 D.7个
6、如图,有6张扑克牌,从中随机抽取一张,点数小于7的可能性大小是( )
A.3 B. C.1 D.
7、现有四张卡片依次写有“郑”“外”“加”“油”四个字(四张卡片除字不同外其他均相同),把四张卡片背面向上洗匀后,从中随机抽取两张,则抽到的汉字给好是“郑”和“外”的概率是( )
A. B. C. D.
8、一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,则估计红球的个数约为( )
A.35个 B.60个 C.70个 D.130个
9、连续抛掷两次骰子,它们的点都是奇数的概率是( )
A. B. C. D.
10、在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干只,某小组做摸球实验:将球搅匀后从中随机摸出一个,记下颜色,再放入袋中,不断重复,右表是活动中的一组数据,则摸到白球的概率约是( )
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 58 96 116 295 484 601
摸到白球的概率 0.58 0.64 0.58 0.59 0.605 0.601
A.0.58 B.0.64 C.0.59 D.0.60
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同,小刚通过多次摸球试验后发现其中摸到红色,黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 _____个.
2、在一个不透明的盒子里装有若干个红球和20个白球,这些球除颜色外其余全部相同,每次从袋子中摸出一球记下颜色后放回,通过多次重复实验发现摸到红球的频率稳定在0.6附近,则袋中红球大约有________个.
3、林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 865 1356 2220 3500 7056 13170 17580 26430
成活的频率 0.865 0.904 0.888 0.875 0.882 0.878 0.879 0.881
估计该种幼树在此条件下移植成活的概率为_______.
4、有6张除数字外无差别的卡片,上面分别写着1,2,3,4,5,6.随机抽取一张记作,放回并混合在一起,再随机抽一张记作,组成有序实数对,则点在直线上的概率为______
5、只有1和它本身两个因数且大于1的自然数叫做质数,我国数学家陈景润在有关质数的“哥德巴赫猜想”的研究中取得了世界领先的成果.从3,5,7,11,13,23这6个质数中随机抽取一个,则抽到个位数是3的可能性是________.
三、解答题(5小题,每小题10分,共计50分)
1、随着手机技术的迅猛发展,人们的沟通方式更便捷、多样.小强和他爸爸要在各自的手机里安装(微信、、钉钉)三种中的一种,用树状图或列表法求他俩选择同一种的概率.
2、为了继续宣传新冠疫苗接种的重要性,某小区物业部门准备在已经接种疫苗的居民中招募2名志愿宣传者,现有2名男性2名女性共4名居民报名.
(1)从4人中抽取1人为男性的概率是______;
(2)请用列表或画树状图的方法,求要从这4人中随机挑选2人,恰好抽到一名男性和一名女性的概率.
3、小颖为元旦联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果一个转盘转出了红色,另一个转盘转出了蓝色,那么游戏者获胜,因为红色和蓝色在一起配成了紫色.如果转盘的指针落在分割线上,则重新转动转盘.用列表或画树状图的方法,求游戏者获胜的概率.
4、某校对八年级学生进行一次垃圾分类知识竞赛,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制不完整的统计图表.
等级 频数(人数) 频率
A a 20%
B 16 40%
C b m
D 4 10%
请你根据统计图表提供的信息解答下列问题:
(1)上表中的a= ,b= ,m= .
(2)本次调查共抽取了 名学生.请补全条形图.
(3)若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.
5、中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是了解我国古代数学的重要文献.
(1)小华想从这4部数学名著中随机选择1部阅读,求他选中《孙子算经》的概率;
(2)某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,用列表法或树状图法求出选中的2部名著中,其中1部是《周髀算经》的概率.
-参考答案-
一、单选题
1、B
【解析】
【分析】
根据树状图展示的所有结果,找出恰好一个红球和一个白球所占结果.
【详解】
由树状图得,从两个口袋中各随机取出一个球共有6种等可能结果,
其中恰好一个红球和一个白球有2种结果.
故选:B.
【点睛】
此题考查的是树状图的知识点,根据树状图展示的所有结果,找到符合条件的结果数是解题的关键.
2、A
【解析】
【分析】
根据题意列出树状图,进而问题可求解.
【详解】
解:由题意可得如下树状图:
∴组成的两位数是偶数的概率为;
故选A.
【点睛】
本题主要考查概率,熟练掌握利用树状图求解概率是解题的关键.
3、C
【解析】
【分析】
根据列表法或树状图法表示出来所有可能,然后找出满足条件的情况,即可得出概率.
【详解】
解:将作业、睡眠、手机、读物、体质“五项管理”简写为:业、睡、机、读、体,利用列表法可得:
业 睡 机 读 体
业 (业,睡) (业,机) (业,读) (业,体)
睡 (睡,业) (睡,机) (睡,读) (睡,体)
机 (机,业) (机,睡) (机,读) (机,体)
读 (读,业) (读,睡) (读,机) (读,体)
体 (体,业) (体,睡) (体,机) (体,读)
根据表格可得:共有20种可能,满足“作业”和“手机”的情况有两种,
∴ 抽到“作业”和“手机”的概率为:,
故选:C.
【点睛】
题目主要考查列表法或树状图法求概率,熟练掌握列表法或树状图法是解题关键.
4、B
【解析】
【分析】
分别计算所有情况数及满足条件的情况数,代入概率计算公式,可得答案.
【详解】
盒子中装有形状、大小完全相同的3个小球,球上分别标有数字-1,1,2,
从中随机取出一个,其上的数字记为,放回后再取一次,其上的数记为,
则共有9种情况,分别为:
(-1,-1),(-1,1),(-1,2),(1,-1),(1,1),(1,2),(2,-1),(2,1),(2,2),
一次函数y=k1x+b与第一象限内y=的增减性一致的有:
(-1,1),(-1,2),
一次函数y=k1x+b与第一象限内y=的增减性一致的概率为
故选B.
【点睛】
此题考查概率计算公式,判断一次函数与反比例函数的增减性,解题关键在于列出所有可能出现的情况.
5、D
【解析】
【分析】
估计利用频率估计概率可估计摸到红球的概率为0.7,然后根据概率公式计算这个口袋中红球的数量.
【详解】
解:因为共摸了200次球,发现有140次摸到红球,
所以估计摸到红球的概率为0.7,
所以估计这个口袋中红球的数量为10×0.7=7(个).
故选:D.
【点睛】
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
6、B
【解析】
【分析】
先用列举法得到所有的等可能的结果数,然后得到小于7的结果数,由此利用概率公式求解即可.
【详解】
解:由题意得:从这6张扑克牌,从中随机抽取一张,点数的可能为:3、4、5、7、8、10,一共6种结果,其中点数小于7的有3、4、5三种结果,
∴P点数小于7
故选B.
【点睛】
本题主要考查了用列举法求解概率,解题的关键在于能够熟练掌握用列举法求解概率.
7、C
【解析】
【分析】
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】
解:列表如下:
郑 外 加 油
郑 外,郑 加,郑 油,郑
外 郑,外 加,外 油,外
加 郑,加 外,加 油,加
油 郑,油 外,油 加,油
由表可知,共有12种等可能结果,其中抽到的汉字恰好是“郑”和“外”的有2种结果,
所以抽到的汉字恰好是“郑”和“外”的概率为.
故选:C.
【点睛】
本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.
8、C
【解析】
【分析】
根据大量重复试验后频率的稳定值即为概率,进行求解即可.
【详解】
解:∵一个口袋中有红色、黄色、蓝色玻璃球共200个,小明通过大量摸球试验后,发现摸到红球的频率为35%,
∴红球的个数=200×35%=70个,
故选C.
【点睛】
本题主要考查了用频率估计概率,解题的关键在于能够熟练掌握大量重复试验下,频率的稳定值即为概率.
9、C
【解析】
【分析】
先列表,求解所有的等可能的结果数与符合条件的结果数,再利用概率公式进行计算即可.
【详解】
解:列表如下:
由表格信息可得:所有的等可能的结果数有个,符合条件的结果数有
故选C
【点睛】
本题考查的是利用列表法求解等可能事件的概率,掌握“列表法”是解本题的关键.
10、D
【解析】
【分析】
根据表格中的数据,随着实验次数的增大,频率逐渐稳定在0.60左右,即为摸出白球的概率.
【详解】
观察表格得:通过多次摸球实验后发现其中摸到白球的频率稳定在0.60左右,则摸到白球的概率约是0.60.
故选D
【点睛】
此题考查了利用频率估计概率,在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近.
二、填空题
1、24
【解析】
【分析】
在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,先求得白球的频率,再乘以总球数求解.
【详解】
解:小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在和,
口袋中白色球的个数很可能是个.
故答案为:24.
【点睛】
本题考查了利用用频率估计概率,解题的关键是要计算出口袋中白色球所占的比例,再计算其个数.
2、30
【解析】
【分析】
设袋中红球有x个,根据题意用红球数除以白球和红球的总数等于红球的频率列出方程即可求出红球数.
【详解】
解:设袋中红球有x个,根据题意,得:
,
解并检验得:x=30.
所以袋中红球有30个.
故答案为:30.
【点睛】
本题考查了利用频率估计概率,解决本题的关键是用频率的集中趋势来估计概率,这个固定的近似值
3、0.880
【解析】
【分析】
大量重复实验的情况下,当频率呈现一定的稳定性时,可以用这一稳定值估计事件发生的概率,据此可解.
【详解】
解:大量重复实验的情况下,当频率呈现一定的稳定性时,可以用这一稳定值估计事件发生的概率,
从上表可以看出,频率成活的频率,即稳定于0.880左右,
∴估计这种幼树移植成活率的概率约为0.88.
故答案为:0.880.
【点睛】
此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.
4、
【解析】
【分析】
画树状图表示所有等可能的结果,再计算点在直线上的概率.
【详解】
解:画树状图为:
共有36种机会均等的结果,其中组成有序实数对,则点在直线上的有4种,所以点在直线上的概率为,
故答案为:.
【点睛】
本题考查用树状图或列表法表示概率,是重要考点,难度较小,掌握相关知识是解题关键.
5、
【解析】
【分析】
先利用列举法求出个位数字是3的所有结果数,然后利用概率公式求解即可.
【详解】
解:从3,5,7,11,13,23这6个质数中随机抽取一个数一共有6种等可能性的结果数,其中抽到个位是3的有3,13,23三种结果数,
∴抽到个位数字是3的概率是,
故答案为:.
【点睛】
本题主要考查了概率的计算,熟练掌握列举法进行概率的计算是解决本题的关键.
三、解答题
1、他俩选择同一种的概率为.
【解析】
【分析】
列表得出所有结果,再由概率公式求解即可.
【详解】
解:根据题意列表如下:
共有9中等可能的结果,其中小强和爸爸选择同一种APP的情况有3种,
∴他俩选择同一种的概率为.
【点睛】
此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
2、 (1)
(2)
【解析】
【分析】
(1)找出从4人中抽取1人的等可能情况,再找出其中抽取1人为男性的情况,利用概率公式计算即可;
(2)列表或画树状图,列出所有等可能的结果,从中找出满足条件的等可能结果,再利用概率公式计算即可.
(1)
解:∵从4人中抽取1人的等可能情况有4种,其中抽取1人为男性的情况有2种,
∴从4人中抽取1人为男性的概率是,
故答案为;
(2)
解:由题可列下表:
由表可知,共有12种等可能的结果,而两个人选中一名男性和一名女性的结果有8种,
∴.
【点睛】
本题考查列举法求概率和列表或画树状图求概率,掌握列举法求概率的方法和列表或画树状图求概率方法与步骤,关键是从中找出满足条件的等可能结果,熟悉概率公式.
3、
【解析】
【分析】
先画出树状图,从而可得游戏的所有等可能的结果,再找出游戏者获胜的结果,然后利用概率公式进行计算即可得.
【详解】
解:设红色、蓝色和黄色分别用表示,画出树状图如下所示:
则这个游戏的所有等可能的结果共有6种,其中,游戏者获胜的结果有2种,
所以游戏者获胜的概率为,
答:游戏者获胜的概率为.
【点睛】
本题考查了利用列举法求概率,正确画出树状图是解题关键.
4、 (1)8,12,30%
(2)40,见解析
(3)
【解析】
【分析】
(1)根据D等级的人数和所占百分比列式计算求出本次调查共抽取的学生人数,即可解决问题;
(2)由(1)的结果求解即可;
(3)画树状图,共有12种等可能的结果,其中抽取的两名学生恰好是一男一女的结果有8种,再由概率公式求解即可.
(1)
解:本次调查共抽取的学生人数为:4÷10%=40(人),
∴a=40×20%=8,b=8+4=12,m=1﹣20%﹣40%﹣10%=30%;
故答案为:8,12,30%;
(2)
解:由(1)得:本次调查共抽取了40名学生,
故答案为:40,
补全条形图如图所示:
(3)
解:画树状图如图:
共有12种等可能的结果,其中抽取的两名学生恰好是一男一女的结果有8种,
∴抽取的两名学生恰好是一男一女的概率为=.
【点睛】
此题考查了树状图法与列表法求概率的知识以及直方图与统计表的知识.用到的知识点为:概率=所求情况数与总情况数之比.
5、 (1)他选中《孙子算经》的概率为
(2)其中1部是《周髀算经》的概率为
【解析】
(1)
小华想从这4部数学名著中随机选择1部阅读,
则他选中《孙子算经》的概率为.
(2)
将四部名著《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》分别记为A,B,C,D,
记其中1部是《周髀算经》为事件M.
用列表法列举出从4部名著中选择2部所能产生的全部结果:
第1部 第2部 A B C D
A
B
C
D
由表中可以看出,所有可能的结果有12种,并且它们出现的可能性相等.
其中事件M的结果有6种,即BA,CA,DA,AB,AC,AD,
.
【点睛】
本题考查了公式法求简单概率,列表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.熟练掌握求概率的方法是解题的关键.
