人教版五年级下册数学长方体和正方体的体积 课件(共54张PPT)
文档属性
| 名称 | 人教版五年级下册数学长方体和正方体的体积 课件(共54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览






文档简介
(共54张PPT)
20XX
第三单元
长方体和正方体
人教版数学五年级下册
体积和体积单位
长方体和正方体的体积
一、复习导入
乌鸦是怎样喝到水的?为什么?
二、探究新知
实验观察:感受物体占据一定空间。
取两个同样大小的玻璃杯
往左边的杯子里面倒满水
取一块鹅卵石放入右边的杯子
把左边杯子里的水倒进右边的杯子里
观察实验,想一想为什么左边杯子里还留有一部分水?
下面的洗衣机、电饭锅和手机,哪个体积最大,哪个体积最小
物体所占空间的大小叫作物体的体积。
上面三个物体,哪个体积最大?哪个体积最小?
二、探究新知
怎样比较下面两个长方体体积的大小呢
这两个长方体看上去体积差不多,无法直接比较大小。
二、探究新知
类比之前学过的长度、面积单位可知,为了测量和比较不同物体的体积,就需要有统一的体积单位。
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm2、dm3和m3。
二、探究新知
认识常用的体积单位:
(1)棱长是1cm的正方体,体积是1cm3。
二、探究新知
一个手指尖的体积大约是1cm3。
(2)棱长是1dm的正方体,体积是1dm3。
粉笔盒的体积接近于1dm3。
二、探究新知
用3根1m长的木条做成一个互成直角的架子,放在墙角,看看1m3有多大。
(3)棱长是1m的正方体,体积是1m3。
二、探究新知
二、探究新知
如果能把它切成大小相同的小正方体就好了。
能不能先测量,再计算出体积呢?
怎样知道一个长方体的体积呢?
二、探究新知
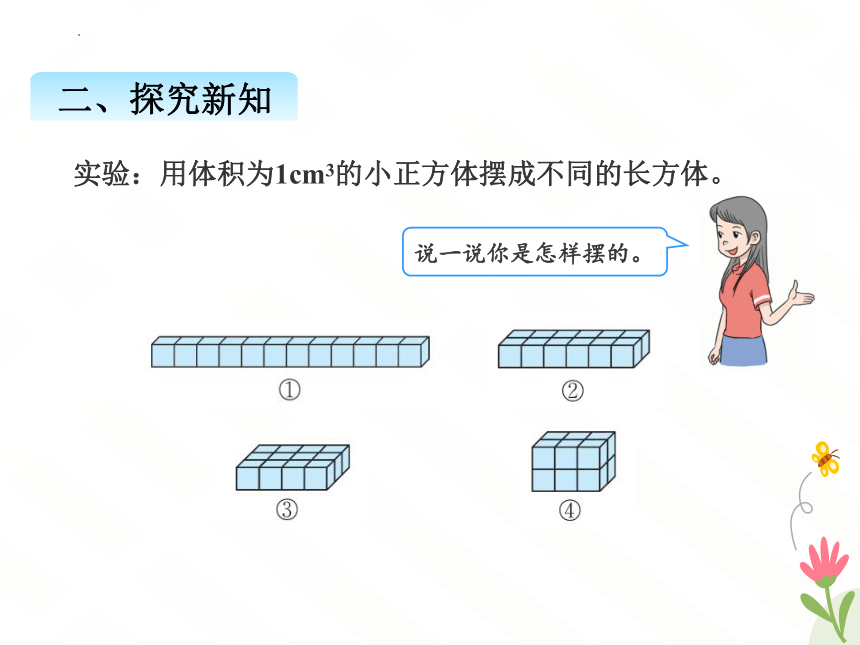
实验:用体积为1cm3的小正方体摆成不同的长方体。
说一说你是怎样摆的。
二、探究新知
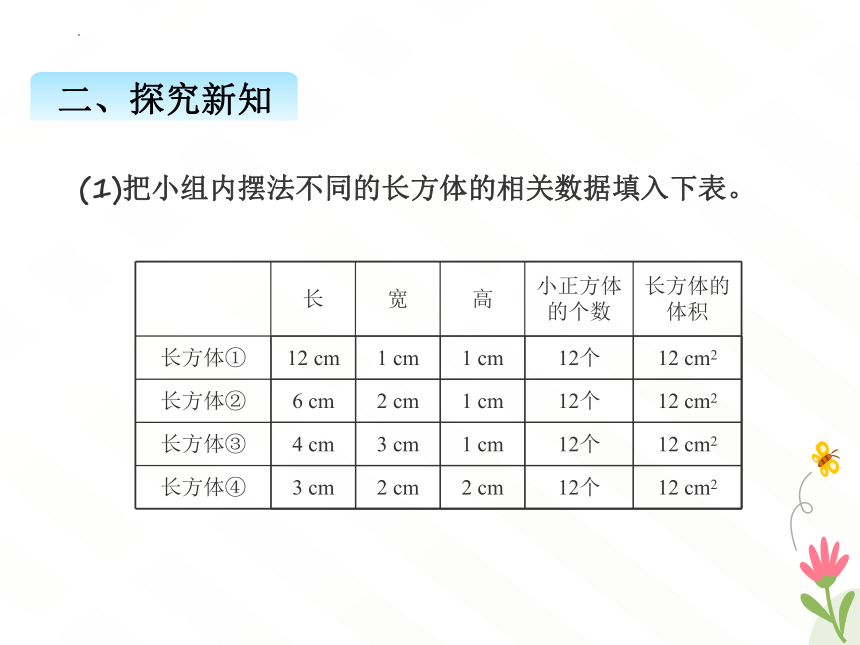
长 宽 高 小正方体的个数 长方体的体积
长方体①
长方体②
长方体③
长方体④
(1)把小组内摆法不同的长方体的相关数据填入下表。
12 cm 1 cm 1 cm 12个 12 cm2
6 cm 2 cm 1 cm 12个 12 cm2
4 cm 3 cm 1 cm 12个 12 cm2
3 cm 2 cm 2 cm 12个 12 cm2
二、探究新知
长方体所含体积单位的个数就是长方体的体积。
长方体的体积正好等于长×宽×高的积。
(2)观察上表:摆出的长方体的体积与长、宽、高有什么关系?
长方体的体积=
长×宽×高
V=a b h
想一想:根据长方体和正方体的关系,正方体的体积应该怎样计算?
二、探究新知
正方体的体积=
棱长×棱长×棱长
正方体的体积公式一般写成: V=a3
a·a·a也可以写作“a3”,读作“a的立方”,表示3个a相乘。
V=a · a · a
二、探究新知
二、探究新知
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=a b h
=6×5×4
=120(dm3)
V=a3
=53
=125(dm3)
二、探究新知
长方体或正方体底面的面积叫作底面积。
长方体的体积=
长×宽×高
底面积
正方体的体积=
棱长×棱长×棱长
底面积
长方体(或正方体)的体积=底面积×高
V = S h
1. 1cm、1cm2、1cm3分别是什么单位,它们有什么不同
长度单位
面积单位
体积单位
三、巩固练习
2. 下面是用棱长1cm的小正方体拼成的几何体,它们的体积各是多少。
9cm3
8cm3
6cm3
4cm3
三、巩固练习
三、巩固练习
3.一块长方体豆腐的尺寸如下图所示,它的体积是多少?
V=a b h
=15×7×5
=525(cm3)
四、课堂小结
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm2、dm3和m3。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体(或正方体)的体积=底面积×高
20XX
第三单元
长方体和正方体
人教版数学五年级下册
体积单位间的进率
长方体和正方体的体积
(1)棱长是1cm的正方体,体积是( )。
(2)棱长是1dm的正方体,体积是( )。
(3)棱长是( )的正方体,体积是1m3。
计量体积要用体积单位,常用的体积单位有( )、( )和( ),可以分别写成( )、( )和( )。
立方厘米
立方分米
立方米
cm3
dm3
m3
1dm3
1m
1cm3
一、复习导入
二、探究新知
下图是一个棱长为1dm的正方体,体积是1dm2。想一想:它的体积是多少立方厘米呢?
如果把它的棱长看作10cm,可以把它分成1000块1cm3的小正方体。
它的底面积是100cm2,高是10cm,100×10,体积是1000cm3。
10×10×10=1000(cm2)
1dm3=_____cm3
1000
1m3=______dm3
1000
仿照上面的方法,你能推算出 1m3等于多少立方分米吗
二、探究新知
计量类型 单位名称 相邻两个单位间的进率
长度 米、分米、厘米
面积 平方米、平方分米、平方厘米
体积 立方米、立方分米、立方厘米
10
100
1000
下面是我们学过的计量单位,请把下表补充完整。
二、探究新知
(1)3.8m3是多少立方分米
想: 1m3= dm3
3.8m3= dm3
(2)2400cm3是多少立方分米
想: cm3=1dm3
2400cm3= dm3
1000
1000
3800
2.4
二、探究新知
下面这个牛奶包装箱的体积是多少
=50×30×40
=60000(cm3)
60000cm3=60dm3=0.06m3
V=a b h
箱上的尺寸表示的是这个长方体的长、宽、高。
50cm
30cm
40cm
二、探究新知
答:这个牛奶包装箱的体积是0.06m3。
3.5dm3=_____ cm3
700dm3=____ m3
3500
0.7
0.25m3=______ cm3
250000
要想清楚单位间的进率哦!
三、巩固练习
1.
2.要砌一面长15m、厚24cm、高3m的砖墙,如果每立方米用砖525块,至少要用砖多少块?
24cm=0.24m
V =a b h
=15×0.24×3
=10.8(m3)
10.8×525=5670(块)
答:至少要用砖5670块。
三、巩固练习
人们很早就得出了长方体、圆柱等立体图形的体积计算公式。我国古代数学名著《九章算术》中,集中而正确地给出了立体图形的体积计算公式。书中在求底面是正方形的长方体体积时,是这样说的:“方自乘,以高乘之即积尺。”就是说,先用边长乘边长得底面积,再乘高就得到长方体的体积。
四、课外拓展
◎ 你知道吗?◎
五、课堂小结
单位名称 相邻两个单位间的进率
长度 米、分米、厘米 10
面积 平方米、平方分米、平方厘米 100
体积 立方米、立方分米、立方厘米 1000
20XX
第三单元
长方体和正方体
人教版数学五年级下册
容积和容积单位
长方体和正方体的体积
物体所占空间的大小叫作物体的( )。
体积
长方体的体积=
长×宽×高
V=a b h
正方体的体积=
棱长×棱长×棱长
V=a3
一、复习导入
箱子、油桶、仓库等所能容纳物体的体积,通常叫作它们的容积。
计量容积一般用体积单位。计量液体(如水、油等)的体积常用容积单位升( L )和毫升( mL ) 。
1L=1000mL
二、探究新知
二、探究新知
下面物品上标注250mL和5L指的是什么?
指的是容器中所盛液体的体积。
可以用量筒或量杯度量液体的体积。
1升液体的体积就是1立方分米,1L=1 dm2
1毫升液体的体积就是1立方厘米,1mL=1 cm2
二、探究新知
(3)说一说在哪些物品上标有毫升、升。
二、探究新知
1L=1dm3
容积单位和体积单位有这样的关系。
1mL=1cm3
二、探究新知
长方体或正方体容器容积的计算方法,跟体积的计算方法相同。但要从容器里面量长、宽、高。
一个长方体油箱,从里面长5dm、宽4dm、高2dm。这个油箱可以装多少升油
5×4×2=40(dm3)
40dm3=40L
答: 这个油箱可以装40L油。
二、探究新知
在横线上填写合适的容积单位。
一瓶墨水约50____
一瓶洗手液约500___
一台冰箱容积约229____
mL
mL
L
“奋斗者”号载人潜水器载人舱的容积约 3____
m3
三、巩固练习
一种微波炉,产品说明书上标明:炉腔内部尺寸400×225×300(单位:mm)。这个微波炉的容积是多少升
4×2.25×3=27(dm3)
27dm3=27L
答:这个微波炉的容积是27L。
400mm=4dm
225mm=2.25dm
300mm=3dm
三、巩固练习
四、课堂小结
容器所能容纳物体的体积,通常叫作它的容积。
常用容积单位升( L )和毫升( mL ) 。1L=1000mL,1L=1dm3,1mL=1cm3。
20XX
第三单元
长方体和正方体
人教版数学五年级下册
不规则物体体积
长方体和正方体的体积
V1张=V100张÷100
一、谈话导入
如何求一张A4纸的体积呢?
可以先求出100张A4纸的体积,再求出一张A4纸的体积。
二、探究新知
设法求出下面两种物体的体积。
阅读与理解
要解决什么问题?这些物体分别有什么特征?
要求橡皮泥和土豆的体积。
橡皮泥和土豆的形状是不规则的,无法直接用长方体或正方体的体积计算公式进行计算。
二、探究新知
可以把橡皮泥捏压成规则的长方体或正方体形状,再求出体积。
分析与解答
把土豆放入量杯里,水面上升部分的体积就是土豆的体积。
这种方法叫排水法。
分析与解答
二、探究新知
水的体积是 mL。
水和土豆的体积是 mL。
250
400
土豆的体积:400-250=150(cm2)
二、探究新知
测量形状不规则的物体体积的方法
等积变形法:
把形状不规则的物体通过捏压等方式转化成规则的长方体或正方体,长方体或正方体的体积就是形状不规则的物体的体积。
排水法:
利用有刻度的量杯记录下放入形状不规则的物体(完全浸没在水中且不溶于水)前后水位的刻度,上升的那部分水的体积就是形状不规则的物体的体积。
可以利用排水法测量乒乓球、冰块的体积吗?为什么?
不可以,因为乒乓球不能完全浸入水中,而冰块在水中可能融化。
二、探究新知
回顾与反思
三、巩固练习
答:珊瑚石的体积是64cm3。
下图中,珊瑚石的体积是多少?
1.
2.求下图中大圆球的体积。
三、巩固练习
答:大圆球的体积是8cm3。
四、课后小结
测量形状不规则的物体体积的方法
等积变形法
排水法
谢谢观看
20XX
第三单元
长方体和正方体
人教版数学五年级下册
体积和体积单位
长方体和正方体的体积
一、复习导入
乌鸦是怎样喝到水的?为什么?
二、探究新知
实验观察:感受物体占据一定空间。
取两个同样大小的玻璃杯
往左边的杯子里面倒满水
取一块鹅卵石放入右边的杯子
把左边杯子里的水倒进右边的杯子里
观察实验,想一想为什么左边杯子里还留有一部分水?
下面的洗衣机、电饭锅和手机,哪个体积最大,哪个体积最小
物体所占空间的大小叫作物体的体积。
上面三个物体,哪个体积最大?哪个体积最小?
二、探究新知
怎样比较下面两个长方体体积的大小呢
这两个长方体看上去体积差不多,无法直接比较大小。
二、探究新知
类比之前学过的长度、面积单位可知,为了测量和比较不同物体的体积,就需要有统一的体积单位。
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm2、dm3和m3。
二、探究新知
认识常用的体积单位:
(1)棱长是1cm的正方体,体积是1cm3。
二、探究新知
一个手指尖的体积大约是1cm3。
(2)棱长是1dm的正方体,体积是1dm3。
粉笔盒的体积接近于1dm3。
二、探究新知
用3根1m长的木条做成一个互成直角的架子,放在墙角,看看1m3有多大。
(3)棱长是1m的正方体,体积是1m3。
二、探究新知
二、探究新知
如果能把它切成大小相同的小正方体就好了。
能不能先测量,再计算出体积呢?
怎样知道一个长方体的体积呢?
二、探究新知
实验:用体积为1cm3的小正方体摆成不同的长方体。
说一说你是怎样摆的。
二、探究新知
长 宽 高 小正方体的个数 长方体的体积
长方体①
长方体②
长方体③
长方体④
(1)把小组内摆法不同的长方体的相关数据填入下表。
12 cm 1 cm 1 cm 12个 12 cm2
6 cm 2 cm 1 cm 12个 12 cm2
4 cm 3 cm 1 cm 12个 12 cm2
3 cm 2 cm 2 cm 12个 12 cm2
二、探究新知
长方体所含体积单位的个数就是长方体的体积。
长方体的体积正好等于长×宽×高的积。
(2)观察上表:摆出的长方体的体积与长、宽、高有什么关系?
长方体的体积=
长×宽×高
V=a b h
想一想:根据长方体和正方体的关系,正方体的体积应该怎样计算?
二、探究新知
正方体的体积=
棱长×棱长×棱长
正方体的体积公式一般写成: V=a3
a·a·a也可以写作“a3”,读作“a的立方”,表示3个a相乘。
V=a · a · a
二、探究新知
二、探究新知
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=a b h
=6×5×4
=120(dm3)
V=a3
=53
=125(dm3)
二、探究新知
长方体或正方体底面的面积叫作底面积。
长方体的体积=
长×宽×高
底面积
正方体的体积=
棱长×棱长×棱长
底面积
长方体(或正方体)的体积=底面积×高
V = S h
1. 1cm、1cm2、1cm3分别是什么单位,它们有什么不同
长度单位
面积单位
体积单位
三、巩固练习
2. 下面是用棱长1cm的小正方体拼成的几何体,它们的体积各是多少。
9cm3
8cm3
6cm3
4cm3
三、巩固练习
三、巩固练习
3.一块长方体豆腐的尺寸如下图所示,它的体积是多少?
V=a b h
=15×7×5
=525(cm3)
四、课堂小结
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm2、dm3和m3。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体(或正方体)的体积=底面积×高
20XX
第三单元
长方体和正方体
人教版数学五年级下册
体积单位间的进率
长方体和正方体的体积
(1)棱长是1cm的正方体,体积是( )。
(2)棱长是1dm的正方体,体积是( )。
(3)棱长是( )的正方体,体积是1m3。
计量体积要用体积单位,常用的体积单位有( )、( )和( ),可以分别写成( )、( )和( )。
立方厘米
立方分米
立方米
cm3
dm3
m3
1dm3
1m
1cm3
一、复习导入
二、探究新知
下图是一个棱长为1dm的正方体,体积是1dm2。想一想:它的体积是多少立方厘米呢?
如果把它的棱长看作10cm,可以把它分成1000块1cm3的小正方体。
它的底面积是100cm2,高是10cm,100×10,体积是1000cm3。
10×10×10=1000(cm2)
1dm3=_____cm3
1000
1m3=______dm3
1000
仿照上面的方法,你能推算出 1m3等于多少立方分米吗
二、探究新知
计量类型 单位名称 相邻两个单位间的进率
长度 米、分米、厘米
面积 平方米、平方分米、平方厘米
体积 立方米、立方分米、立方厘米
10
100
1000
下面是我们学过的计量单位,请把下表补充完整。
二、探究新知
(1)3.8m3是多少立方分米
想: 1m3= dm3
3.8m3= dm3
(2)2400cm3是多少立方分米
想: cm3=1dm3
2400cm3= dm3
1000
1000
3800
2.4
二、探究新知
下面这个牛奶包装箱的体积是多少
=50×30×40
=60000(cm3)
60000cm3=60dm3=0.06m3
V=a b h
箱上的尺寸表示的是这个长方体的长、宽、高。
50cm
30cm
40cm
二、探究新知
答:这个牛奶包装箱的体积是0.06m3。
3.5dm3=_____ cm3
700dm3=____ m3
3500
0.7
0.25m3=______ cm3
250000
要想清楚单位间的进率哦!
三、巩固练习
1.
2.要砌一面长15m、厚24cm、高3m的砖墙,如果每立方米用砖525块,至少要用砖多少块?
24cm=0.24m
V =a b h
=15×0.24×3
=10.8(m3)
10.8×525=5670(块)
答:至少要用砖5670块。
三、巩固练习
人们很早就得出了长方体、圆柱等立体图形的体积计算公式。我国古代数学名著《九章算术》中,集中而正确地给出了立体图形的体积计算公式。书中在求底面是正方形的长方体体积时,是这样说的:“方自乘,以高乘之即积尺。”就是说,先用边长乘边长得底面积,再乘高就得到长方体的体积。
四、课外拓展
◎ 你知道吗?◎
五、课堂小结
单位名称 相邻两个单位间的进率
长度 米、分米、厘米 10
面积 平方米、平方分米、平方厘米 100
体积 立方米、立方分米、立方厘米 1000
20XX
第三单元
长方体和正方体
人教版数学五年级下册
容积和容积单位
长方体和正方体的体积
物体所占空间的大小叫作物体的( )。
体积
长方体的体积=
长×宽×高
V=a b h
正方体的体积=
棱长×棱长×棱长
V=a3
一、复习导入
箱子、油桶、仓库等所能容纳物体的体积,通常叫作它们的容积。
计量容积一般用体积单位。计量液体(如水、油等)的体积常用容积单位升( L )和毫升( mL ) 。
1L=1000mL
二、探究新知
二、探究新知
下面物品上标注250mL和5L指的是什么?
指的是容器中所盛液体的体积。
可以用量筒或量杯度量液体的体积。
1升液体的体积就是1立方分米,1L=1 dm2
1毫升液体的体积就是1立方厘米,1mL=1 cm2
二、探究新知
(3)说一说在哪些物品上标有毫升、升。
二、探究新知
1L=1dm3
容积单位和体积单位有这样的关系。
1mL=1cm3
二、探究新知
长方体或正方体容器容积的计算方法,跟体积的计算方法相同。但要从容器里面量长、宽、高。
一个长方体油箱,从里面长5dm、宽4dm、高2dm。这个油箱可以装多少升油
5×4×2=40(dm3)
40dm3=40L
答: 这个油箱可以装40L油。
二、探究新知
在横线上填写合适的容积单位。
一瓶墨水约50____
一瓶洗手液约500___
一台冰箱容积约229____
mL
mL
L
“奋斗者”号载人潜水器载人舱的容积约 3____
m3
三、巩固练习
一种微波炉,产品说明书上标明:炉腔内部尺寸400×225×300(单位:mm)。这个微波炉的容积是多少升
4×2.25×3=27(dm3)
27dm3=27L
答:这个微波炉的容积是27L。
400mm=4dm
225mm=2.25dm
300mm=3dm
三、巩固练习
四、课堂小结
容器所能容纳物体的体积,通常叫作它的容积。
常用容积单位升( L )和毫升( mL ) 。1L=1000mL,1L=1dm3,1mL=1cm3。
20XX
第三单元
长方体和正方体
人教版数学五年级下册
不规则物体体积
长方体和正方体的体积
V1张=V100张÷100
一、谈话导入
如何求一张A4纸的体积呢?
可以先求出100张A4纸的体积,再求出一张A4纸的体积。
二、探究新知
设法求出下面两种物体的体积。
阅读与理解
要解决什么问题?这些物体分别有什么特征?
要求橡皮泥和土豆的体积。
橡皮泥和土豆的形状是不规则的,无法直接用长方体或正方体的体积计算公式进行计算。
二、探究新知
可以把橡皮泥捏压成规则的长方体或正方体形状,再求出体积。
分析与解答
把土豆放入量杯里,水面上升部分的体积就是土豆的体积。
这种方法叫排水法。
分析与解答
二、探究新知
水的体积是 mL。
水和土豆的体积是 mL。
250
400
土豆的体积:400-250=150(cm2)
二、探究新知
测量形状不规则的物体体积的方法
等积变形法:
把形状不规则的物体通过捏压等方式转化成规则的长方体或正方体,长方体或正方体的体积就是形状不规则的物体的体积。
排水法:
利用有刻度的量杯记录下放入形状不规则的物体(完全浸没在水中且不溶于水)前后水位的刻度,上升的那部分水的体积就是形状不规则的物体的体积。
可以利用排水法测量乒乓球、冰块的体积吗?为什么?
不可以,因为乒乓球不能完全浸入水中,而冰块在水中可能融化。
二、探究新知
回顾与反思
三、巩固练习
答:珊瑚石的体积是64cm3。
下图中,珊瑚石的体积是多少?
1.
2.求下图中大圆球的体积。
三、巩固练习
答:大圆球的体积是8cm3。
四、课后小结
测量形状不规则的物体体积的方法
等积变形法
排水法
谢谢观看
