人教版七年级数学上册:2.1 整式 教学设计(3课时)
文档属性
| 名称 | 人教版七年级数学上册:2.1 整式 教学设计(3课时) |  | |
| 格式 | zip | ||
| 文件大小 | 52.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-16 16:27:40 | ||
图片预览


文档简介
第二章 整式的加减
2.1 整式
第1课时 用字母表示数
教学目标:
1.认识用字母表示数.
2.会用含字母的式子表示数量关系.
教学重难点:会用字母表示数量关系.
教学过程:
一、创设问题情境,引入新课
1.阅读课本P53,本章引言中的问题:
问题1:用s表示路程,v表示速度,t表示行驶时间,这三个量之间存在什么样的关系式
问题2:用S表示圆的面积,C表示圆的周长,r表示圆的半径,用含r的式子表示S和C.
问题3:a和b表示两个有理数,用字母表示加法交换律.
问题4:全班共有学生x人,其中女生人数占54%,女生人数和男生人数分别是多少 用含x的式子表示.
2.合作交流以上问题、思考:
(1)字母可以表示什么
(2)用字母表示数的作用.
3.总结归纳:用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
4.课本P54例1、P55例2.
(1)学生独立完成.
(2)交流,有困难的学生组内讨论帮助.
二、反馈练习
1.课本P56练习第1~4题.
2.能力提升练习.
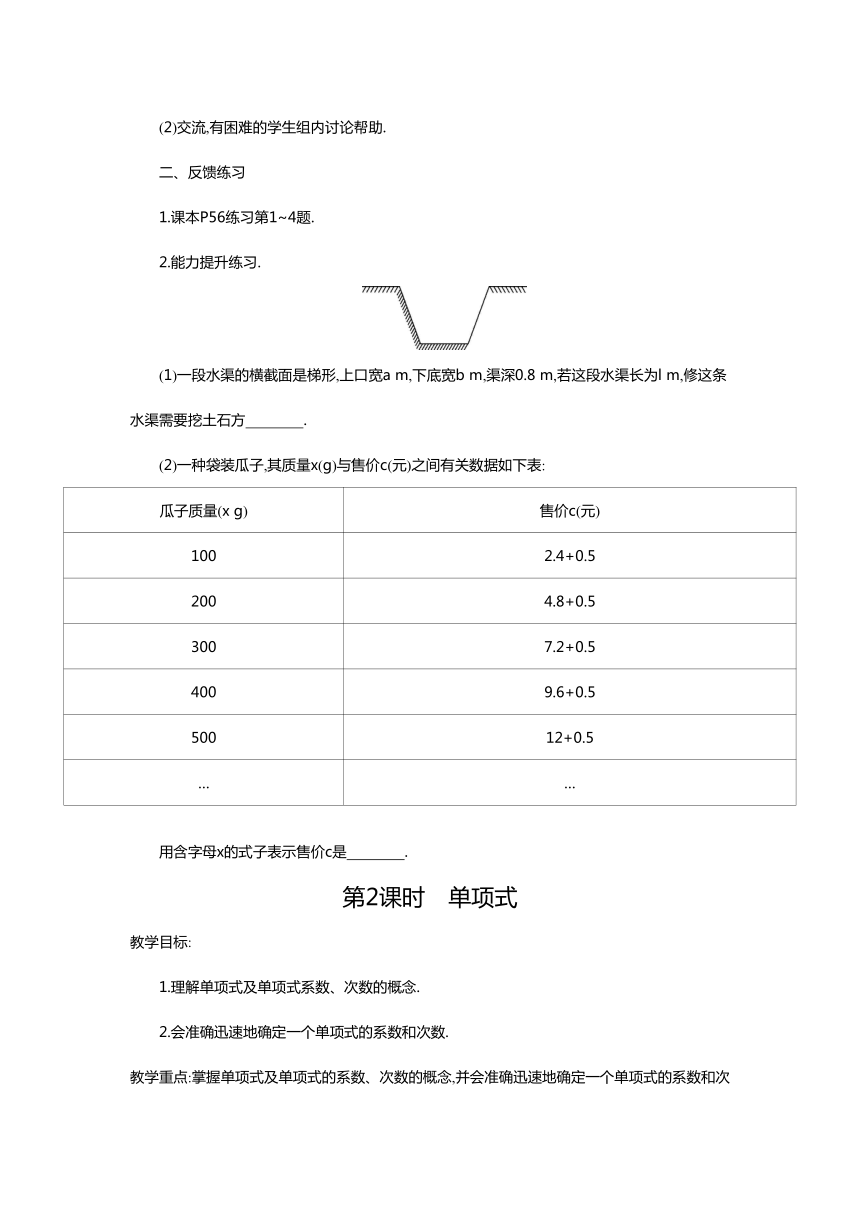
(1)一段水渠的横截面是梯形,上口宽a m,下底宽b m,渠深0.8 m,若这段水渠长为l m,修这条水渠需要挖土石方 .
(2)一种袋装瓜子,其质量x(g)与售价c(元)之间有关数据如下表:
瓜子质量(x g) 售价c(元)
100 2.4+0.5
200 4.8+0.5
300 7.2+0.5
400 9.6+0.5
500 12+0.5
… …
用含字母x的式子表示售价c是 .
第2课时 单项式
教学目标:
1.理解单项式及单项式系数、次数的概念.
2.会准确迅速地确定一个单项式的系数和次数.
教学重点:掌握单项式及单项式的系数、次数的概念,并会准确迅速地确定一个单项式的系数和次数.
教学难点:单项式概念的建立.
教学过程:
一、复习引入
1.列代数式
(1)若正方体的边长为a,则正方体的面积是 ;
(2)若三角形一边长为a,并且这边上的高为h,则这个三角形的面积为 ;
(3)若x表示正方体的棱长,则正方体的体积是 ;
(4)若m表示一个有理数,则它的相反数是 .
2.请学生说出所列代数式的意义.
3.请学生观察所列代数式包含哪些运算,有何共同运算特征.
二、讲授新课
1.单项式:
通过特征的描述,引导学生概括单项式的概念 ( http: / / www.21cnjy.com ),从而引入课题:单项式,并板书归纳得出的单项式的概念,即由数与字母的乘积组成的代数式称为单项式.然后教师作补充:单独一个数或一个字母也是单项式,如a,5.
2.练习:判断下列各代数式中哪些是单项式
(1) ; (2)abc; (3)b2; (4)-5ab2;
(5)y; (6)-xy2; (7)-5.
3.单项式的系数和次数:
直接引导学生进一步观察单项式的结构,总结出 ( http: / / www.21cnjy.com )单项式是由数字因数和字母因数两部分组成的.以四个单项式a2h,2πr,abc,-m为例,让学生说出它们的数字因数是什么,从而引入单项式系数的概念并板书,接着让学生说出以上几个单项式的字母因数是什么,各字母的指数分别是多少,从而引入单项式次数的概念并板书.
4.例题:
【例1】判断下列各代数式是否是单项式.如不是,请说明理由;如果是,请指出它的系数和次数.
(1)x+1; (2); (3)πr2; (4)-a2b.
【例2】下面各题的判断是否正确
(1)-7xy2的系数是7;
(2)-x2y3与x3没有系数;
(3)-ab3c2的次数是0+3+2;
(4)-a3的系数是-1;
(5)-32x2y3的次数是7;
(6)πr2h的系数是.
通过其中的反例练习及例题,强调应注意以下几点:
(1)圆周率π是常数.
(2)当一个单项式的系数是1或-1时,“1”通常省略不写,如x2,-a2b等.
(3)单项式次数只与字母指数有关.
5.课堂练习:课本P57练习第1、2题.
三、课时小结
1.单项式及单项式的系数、次数.
2.根据教学过程反馈的信息,对出现的问题有针对性地进行小结.
四、课堂作业
课本P59习题2.1的第1、2题.
第3课时 多项式和整式
教学目标:
1.通过本节课的学习,使学生掌握整式、多项式的项及其次数、常数项的概念.
2.初步体会类比和逆向思维的数学思想.
教学重点:掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数以及常数项等概念.
教学难点:准确指出多项式的次数.
教学过程
一、复习引入
1.列代数式:
(1)长方形的长与宽分别为a、b,则长方形的周长是 ;
(2)某班有男生x人,女生21人,则这个班共有学生 人;
(3)图中阴影部分的面积为 ;
( http: / / www.21cnjy.com )
(4)鸡兔同笼,鸡a只,兔b只,则共有头 个,脚 只.
2.观察以上所得出的四个代数式与上节课所学单项式有何区别.
(1)2(a+b); (2)21+x; (3)ab-π()2;
(4)2a+4b.
二、讲授新课
1.多项式:
板书由学生自己归纳得出的多项式概念.上面这 ( http: / / www.21cnjy.com )些代数式都是由几个单项式相加而成的.像这样,几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.其中,不含字母的项,叫做常数项.例如,多项3x2-2x+5有三项,它们是3x2,-2x,5,其中5是常数项.
一个多项式含有几项,就叫几项式.多项式里,次数最高项的次数,就是这个多项式的次数.例如,多项式3x2-2x+5是一个二次三项式.
注意:
(1)多项式的次数不是所有项的次数之和.
(2)多项式的每一项都包括它前面的符号.
2.例题:
【例1】判断:
①多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;
②多项式3n4-2n2+1的次数为4,常数项为1.
【例2】指出下列多项式的项和次数:
(1)3x-1+3x2; (2)4x3+2x-2y2.
【例3】指出下列多项式是几次几项式.
(1)x3-x+1; (2)x3-2x2y2+3y2.
【例4】已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的值.
注意:
多项式的项包括前面的符号, ( http: / / www.21cnjy.com )多项式的次数应为最高次项的次数.在例3讲完后插入整式的定义:单项式与多项式统称整式.分析例4时要紧扣多项式的定义,培养学生的逆向思维,使学生透彻理解多项式的有关概念,培养他们应用新知识解决问题的能力.
【例5】一条河流的水流速度为2.5千米 ( http: / / www.21cnjy.com )/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示 如果甲、乙两船在静水中的速度分别是20千米/时和35千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度各是多少
3.课堂练习:课本P58练习第1、2题.
填空:-a2b-ab+1是 ( http: / / www.21cnjy.com )次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 .
三、课时小结
1.理解多项式的定义,能说出一个多项式是几次几项式,最高次数是几,分别由哪几项组成,各项的系数分别为多少,常数项为几.
2.这堂课学习了多项式,与前一节所学的单项式合起来统称为整式,使知识形成了系统.
(让学生小结,师生进行补充.)
四、课堂作业
课本P59习题2.1的第3、4题.
2.1 整式
第1课时 用字母表示数
教学目标:
1.认识用字母表示数.
2.会用含字母的式子表示数量关系.
教学重难点:会用字母表示数量关系.
教学过程:
一、创设问题情境,引入新课
1.阅读课本P53,本章引言中的问题:
问题1:用s表示路程,v表示速度,t表示行驶时间,这三个量之间存在什么样的关系式
问题2:用S表示圆的面积,C表示圆的周长,r表示圆的半径,用含r的式子表示S和C.
问题3:a和b表示两个有理数,用字母表示加法交换律.
问题4:全班共有学生x人,其中女生人数占54%,女生人数和男生人数分别是多少 用含x的式子表示.
2.合作交流以上问题、思考:
(1)字母可以表示什么
(2)用字母表示数的作用.
3.总结归纳:用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
4.课本P54例1、P55例2.
(1)学生独立完成.
(2)交流,有困难的学生组内讨论帮助.
二、反馈练习
1.课本P56练习第1~4题.
2.能力提升练习.
(1)一段水渠的横截面是梯形,上口宽a m,下底宽b m,渠深0.8 m,若这段水渠长为l m,修这条水渠需要挖土石方 .
(2)一种袋装瓜子,其质量x(g)与售价c(元)之间有关数据如下表:
瓜子质量(x g) 售价c(元)
100 2.4+0.5
200 4.8+0.5
300 7.2+0.5
400 9.6+0.5
500 12+0.5
… …
用含字母x的式子表示售价c是 .
第2课时 单项式
教学目标:
1.理解单项式及单项式系数、次数的概念.
2.会准确迅速地确定一个单项式的系数和次数.
教学重点:掌握单项式及单项式的系数、次数的概念,并会准确迅速地确定一个单项式的系数和次数.
教学难点:单项式概念的建立.
教学过程:
一、复习引入
1.列代数式
(1)若正方体的边长为a,则正方体的面积是 ;
(2)若三角形一边长为a,并且这边上的高为h,则这个三角形的面积为 ;
(3)若x表示正方体的棱长,则正方体的体积是 ;
(4)若m表示一个有理数,则它的相反数是 .
2.请学生说出所列代数式的意义.
3.请学生观察所列代数式包含哪些运算,有何共同运算特征.
二、讲授新课
1.单项式:
通过特征的描述,引导学生概括单项式的概念 ( http: / / www.21cnjy.com ),从而引入课题:单项式,并板书归纳得出的单项式的概念,即由数与字母的乘积组成的代数式称为单项式.然后教师作补充:单独一个数或一个字母也是单项式,如a,5.
2.练习:判断下列各代数式中哪些是单项式
(1) ; (2)abc; (3)b2; (4)-5ab2;
(5)y; (6)-xy2; (7)-5.
3.单项式的系数和次数:
直接引导学生进一步观察单项式的结构,总结出 ( http: / / www.21cnjy.com )单项式是由数字因数和字母因数两部分组成的.以四个单项式a2h,2πr,abc,-m为例,让学生说出它们的数字因数是什么,从而引入单项式系数的概念并板书,接着让学生说出以上几个单项式的字母因数是什么,各字母的指数分别是多少,从而引入单项式次数的概念并板书.
4.例题:
【例1】判断下列各代数式是否是单项式.如不是,请说明理由;如果是,请指出它的系数和次数.
(1)x+1; (2); (3)πr2; (4)-a2b.
【例2】下面各题的判断是否正确
(1)-7xy2的系数是7;
(2)-x2y3与x3没有系数;
(3)-ab3c2的次数是0+3+2;
(4)-a3的系数是-1;
(5)-32x2y3的次数是7;
(6)πr2h的系数是.
通过其中的反例练习及例题,强调应注意以下几点:
(1)圆周率π是常数.
(2)当一个单项式的系数是1或-1时,“1”通常省略不写,如x2,-a2b等.
(3)单项式次数只与字母指数有关.
5.课堂练习:课本P57练习第1、2题.
三、课时小结
1.单项式及单项式的系数、次数.
2.根据教学过程反馈的信息,对出现的问题有针对性地进行小结.
四、课堂作业
课本P59习题2.1的第1、2题.
第3课时 多项式和整式
教学目标:
1.通过本节课的学习,使学生掌握整式、多项式的项及其次数、常数项的概念.
2.初步体会类比和逆向思维的数学思想.
教学重点:掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数以及常数项等概念.
教学难点:准确指出多项式的次数.
教学过程
一、复习引入
1.列代数式:
(1)长方形的长与宽分别为a、b,则长方形的周长是 ;
(2)某班有男生x人,女生21人,则这个班共有学生 人;
(3)图中阴影部分的面积为 ;
( http: / / www.21cnjy.com )
(4)鸡兔同笼,鸡a只,兔b只,则共有头 个,脚 只.
2.观察以上所得出的四个代数式与上节课所学单项式有何区别.
(1)2(a+b); (2)21+x; (3)ab-π()2;
(4)2a+4b.
二、讲授新课
1.多项式:
板书由学生自己归纳得出的多项式概念.上面这 ( http: / / www.21cnjy.com )些代数式都是由几个单项式相加而成的.像这样,几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.其中,不含字母的项,叫做常数项.例如,多项3x2-2x+5有三项,它们是3x2,-2x,5,其中5是常数项.
一个多项式含有几项,就叫几项式.多项式里,次数最高项的次数,就是这个多项式的次数.例如,多项式3x2-2x+5是一个二次三项式.
注意:
(1)多项式的次数不是所有项的次数之和.
(2)多项式的每一项都包括它前面的符号.
2.例题:
【例1】判断:
①多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;
②多项式3n4-2n2+1的次数为4,常数项为1.
【例2】指出下列多项式的项和次数:
(1)3x-1+3x2; (2)4x3+2x-2y2.
【例3】指出下列多项式是几次几项式.
(1)x3-x+1; (2)x3-2x2y2+3y2.
【例4】已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的值.
注意:
多项式的项包括前面的符号, ( http: / / www.21cnjy.com )多项式的次数应为最高次项的次数.在例3讲完后插入整式的定义:单项式与多项式统称整式.分析例4时要紧扣多项式的定义,培养学生的逆向思维,使学生透彻理解多项式的有关概念,培养他们应用新知识解决问题的能力.
【例5】一条河流的水流速度为2.5千米 ( http: / / www.21cnjy.com )/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示 如果甲、乙两船在静水中的速度分别是20千米/时和35千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度各是多少
3.课堂练习:课本P58练习第1、2题.
填空:-a2b-ab+1是 ( http: / / www.21cnjy.com )次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 .
三、课时小结
1.理解多项式的定义,能说出一个多项式是几次几项式,最高次数是几,分别由哪几项组成,各项的系数分别为多少,常数项为几.
2.这堂课学习了多项式,与前一节所学的单项式合起来统称为整式,使知识形成了系统.
(让学生小结,师生进行补充.)
四、课堂作业
课本P59习题2.1的第3、4题.
