青岛版八年级上册数学第1章 全等三角形检测题(word解析版)
文档属性
| 名称 | 青岛版八年级上册数学第1章 全等三角形检测题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 228.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-15 07:46:12 | ||
图片预览



文档简介
单元评价检测(一)
第1章
(45分钟 100分)
一、选择题(每小题4分,共28分)
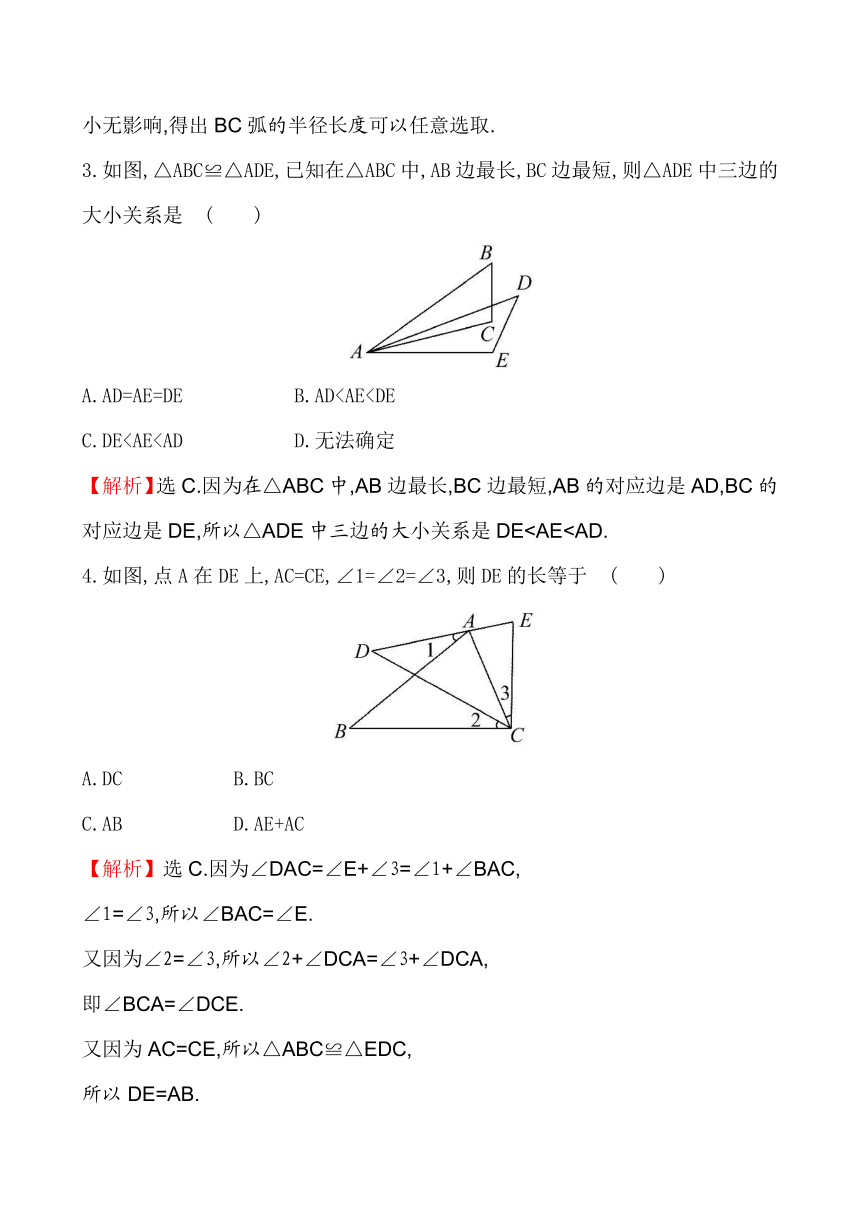
1.下列每组中的两个图形,是全等图形的是 ( )
( http: / / www.21cnjy.com )
【解析】选C.把握全等图形的定义,形状和大小完全相同的两个图形全等,与图形的位置无关.
2.如图所示的是已知∠BAC,求作∠EDF的作图痕迹,则下列说法正确的是( )
( http: / / www.21cnjy.com )
A.因为边的长度对角的大小无影响,所以BC弧的半径长度可以任意选取
B.因为边的长度对角的大小无影响,所以DE弧的半径长度可以任意选取
C.因为边的长度对角的大小无影响,所以FE弧的半径长度可以任意选取
D.以上三种说法都正确
【解析】选A.因为已知∠BAC,求作∠EDF的作图痕迹,所以边的长度对角的大小无影响,得出BC弧的半径长度可以任意选取.
3.如图,△ABC≌△ADE,已知在△ABC中,AB边最长,BC边最短,则△ADE中三边的大小关系是 ( )
( http: / / www.21cnjy.com )
A.AD=AE=DE B.ADC.DE【解析】选C.因为在△ABC中,AB边最 ( http: / / www.21cnjy.com )长,BC边最短,AB的对应边是AD,BC的对应边是DE,所以△ADE中三边的大小关系是DE4.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则DE的长等于 ( )
( http: / / www.21cnjy.com )
A.DC B.BC
C.AB D.AE+AC
【解析】选C.因为∠DAC=∠E+∠3=∠1+∠BAC,
∠1=∠3,所以∠BAC=∠E.
又因为∠2=∠3,所以∠2+∠DCA=∠3+∠DCA,
即∠BCA=∠DCE.
又因为AC=CE,所以△ABC≌△EDC,
所以DE=AB.
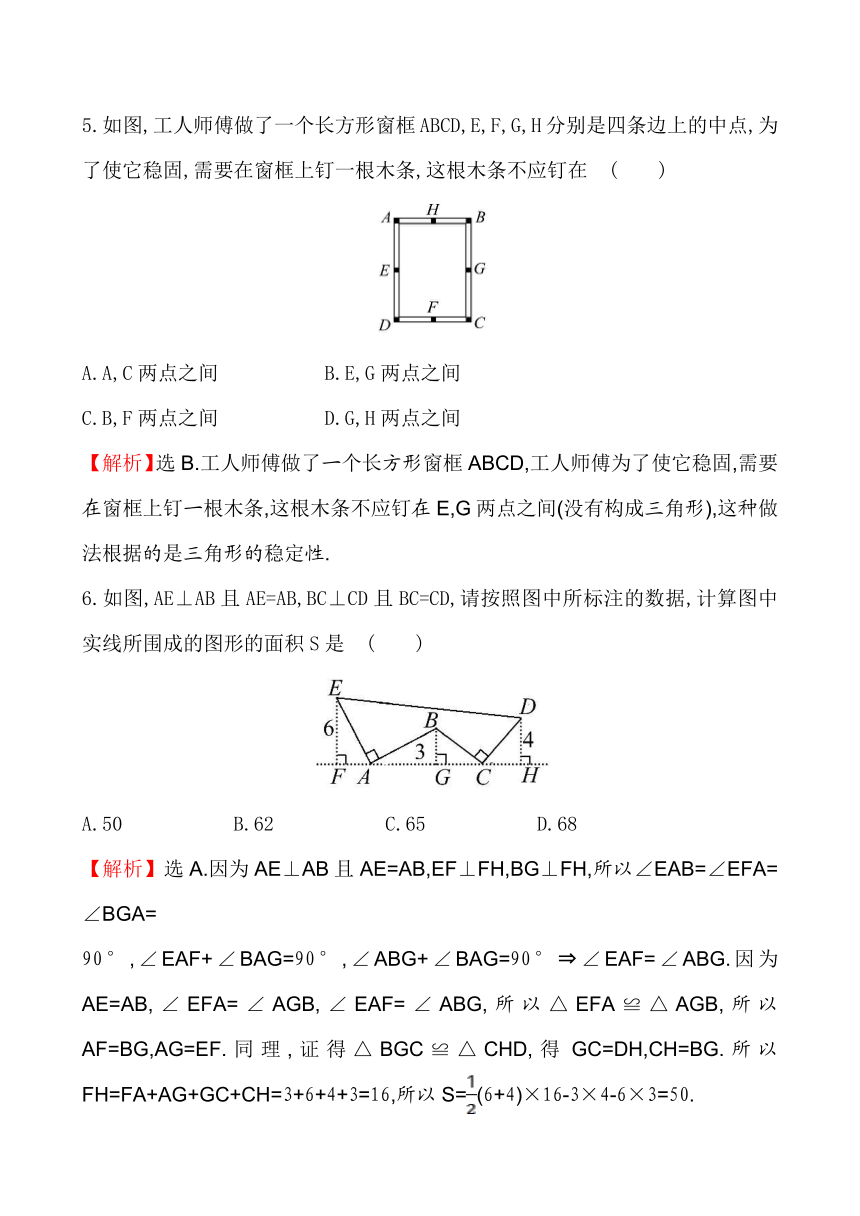
5.如图,工人师傅做了一个长方形窗框ABC ( http: / / www.21cnjy.com )D,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在 ( )
( http: / / www.21cnjy.com )
A.A,C两点之间 B.E,G两点之间
C.B,F两点之间 D.G,H两点之间
【解析】选B.工人师傅做了一个长方形窗框A ( http: / / www.21cnjy.com )BCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E,G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
6.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 ( )
( http: / / www.21cnjy.com )
A.50 B.62 C.65 D.68
【解析】选A.因为AE⊥AB且AE=AB,EF⊥FH,BG⊥FH,所以∠EAB=∠EFA=∠BGA=
90°,∠EAF+∠BAG=90°,∠ABG+∠BAG=90° ∠EAF=∠ABG.因为AE=AB,∠EFA=∠AGB,∠EAF=∠ABG,所以△EFA≌△AGB,所以AF=BG,AG=EF.同理,证得△BGC≌△CHD,得GC=DH,CH=BG.所以FH=FA+AG+GC+CH=3+6+4+3=16,所以S=(6+4)×16-3×4-6×3=50.
7.如图所示,在△ABC中 ( http: / / www.21cnjy.com ),AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,已知EH=EB=3,AE=4,则CH的长是 ( )
( http: / / www.21cnjy.com )
A.1 B.2
C.3 D.4
【解析】选A.因为AD⊥BC,CE⊥AB,
所以∠ADB=∠CEB=90°,
所以∠BAD+∠B=90°,∠ECB+∠B=90°.
所以∠BAD=∠ECB,
在△AEH和△CEB中,
所以△AEH≌△CEB,所以CE=AE=4,
又因为EH=3,所以CH=1.
二、填空题(每小题5分,共25分)
8.如图所示的图案是由全等的图形拼成的,其中AD=0.5cm,BC=1cm,则AF=
cm.
( http: / / www.21cnjy.com )
【解析】由题可知,图中有8个全等的梯形,所以AF=4AD+4BC=4×0.5+4×1=6(cm).
答案:6
9.如图所示,AD,BC相交于点O,△AOB≌△DOC,A,D为对应顶点,则∠C的度数为 .
( http: / / www.21cnjy.com )
【解析】因为△AOB≌△DOC,A,D为对应顶点,所以∠C=∠B,由图知∠B=30°,所以∠C的度数为30°.
答案:30°
【互动探究】如图所示,AD,BC相交于点O,∠A=∠D,AO=DO,则∠C的度数为 .
( http: / / www.21cnjy.com )
【解析】因为∠A=∠D,AO=DO,∠AOB=∠DOC,所以△AOB≌△DOC(ASA),B,C为对应顶点,所以∠C=∠B,
由图知∠B=30°,所以∠C的度数为30°.
答案:30°
10.(2013·天津中考)如图,已知 ( http: / / www.21cnjy.com )∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,请写出图中一组相等的线段 .
( http: / / www.21cnjy.com )
【解析】因为∠C=∠D,∠ABC= ( http: / / www.21cnjy.com )∠BAD,AB=BA,所以△ADB≌△BCA,所以AC=BD,BC=AD,又∠DOA=∠COB,所以△ADO≌△BCO,所以OA=OB,OC=OD.
答案:AC=BD(或BC=AD或OD=OC或OA=OB,答案不唯一)
【变式训练】如图为八个全等的正六边形紧密排列在同一平面上的情形.根据图中标示的各点位置,判断△ACD与下列哪一个三角形全等 ( )
( http: / / www.21cnjy.com )
A.△ACF B.△ADE
C.△ABC D.△BCF
【解析】选B.根据图象可知△ACD和△ADE全等,理由是:因为根据图形可知AD=AD,AE=AC,DE=DC,所以△ACD≌△AED.
11.如图,∠DAB=∠EAC=6 ( http: / / www.21cnjy.com )0°,AB=AD,AC=AE,BE和CD相交于点O,AB和CD相交于P,AC和BE相交于F,则∠DOE的度数是 .
( http: / / www.21cnjy.com )
【解析】因为∠DAB=∠EAC=60°,
所以∠DAB+∠BAC=∠BAC+∠EAC,
所以∠DAC=∠EAB,
在△ADC和△ABE中,
所以△ADC≌△ABE(SAS),所以∠E=∠ACD.
又因为∠AFE=∠OFC,所以∠COF=∠EAF=60°,
所以∠DOE=120°.
答案:120°
12.如图,点E,F分别在∠CAB的边AC,AB上,若AB=AC,AE=AF,BE与CF交于点D,给出结论:
①△ABE≌△ACF;②BD=DE;
③△BDF≌△CDE;④点D在∠BAC的平分线上.
其中正确的结论有 (填写序号).
( http: / / www.21cnjy.com )
【解析】在△CAF和△BAE中,
因为
所以△CAF≌△BAE(SAS),
即△ABE≌△ACF,所以①正确;
根据已知条件不能推出BD=DE,所以②错误;
因为△ABE≌△ACF,所以∠C=∠B.
因为AC=AB,AE=AF,所以CE=BF.
又因为∠CDE=∠BDF,所以△CDE≌△BDF(AAS),所以③正确;
如图,连接AD.
因为△CDE≌△BDF,
所以DE=DF.
因为AE=AF,AD=AD,
所以△EAD≌△FAD(SSS).
所以∠EAD=∠FAD,
即点D在∠BAC的平分线上,
所以④正确.
答案:①③④
三、解答题(共47分)
13.(10分)如图,△ABC≌△ADE,∠CAD=10°,∠B=∠D=25°,∠EAB=120°,试求∠ACB的度数.
( http: / / www.21cnjy.com )
【解析】因为△ABC≌△ADE,所以∠CAB ( http: / / www.21cnjy.com )=∠EAD.因为∠EAB=120°,∠CAD=10°,所以∠EAB=∠EAD+∠CAD+∠CAB=2∠CAB+10°=120°,所以∠CAB=55°.因为
∠B=∠D=25°,所以∠ACB=180°-∠CAB-∠B=180°-55°-25°=100°.
14.(12分)(2014·宁德质检)如图,点A,D,B,E在同一条直线上,AC=DF,AD=BE.AC∥DF.
( http: / / www.21cnjy.com )
试说明:BC=EF.
【解析】因为AC∥DF,
所以∠A=∠FDE,
又因为AD=BE,所以AB=DE,
在△ABC和△DEF中
所以△ABC≌△DEF,所以BC=EF.
15.(12分)(2014·张家口一模)如图,已知△ABC中,∠ABC=45°,AD是BC边上的高,
( http: / / www.21cnjy.com )
(1)尺规作图:在∠ABC的内部作∠CBM,使得∠CBM=∠DAC(要求:只保留作图痕迹,不写作法和理由).
(2)若射线BM与AC交于点E,与AD交于点F,且CD=3,试求线段DF的长.
【解析】(1)作图如图1:
( http: / / www.21cnjy.com )
(2)如图2:
( http: / / www.21cnjy.com )
因为AD⊥BC,∠ABC=45°,
所以∠1=∠ABC=45°,所以AD=BD.
在△BDF和△ADC中,
所以
所以△BDF≌△ADC(ASA),
所以DF=DC=3.
16.(13分)如图所示, ( http: / / www.21cnjy.com )甲、乙二人同时从O点以相同的速度出发,甲沿正东方向前进,乙沿东北方向前进,到某一时刻他们同时改变方向,甲沿正北方向前进,乙沿东南方向前进,他们的速度均保持不变,问他们相遇时在出发点的什么方向
( http: / / www.21cnjy.com )
【解析】连接OC,由题意知,OA=OB,AC=BC.
在△OAC和△OBC中,
所以△OAC≌△OBC(SSS),所以∠AOC=∠BOC.
又∠AOB=45°,所以∠AOC=∠BOC=∠AOB=22.5°,所以∠MOC=45°+22.5°=67.5°,即他们相遇时在出发点的北偏东67.5°方向上.
( http: / / www.21cnjy.com )
【知识归纳】解图形运动问题的思路
对于几何图形的运动问题以 ( http: / / www.21cnjy.com )及一些规律探究题,常常会出现一个基本图形,无论从图形上还是从解题方法上都比较简单,而其他的较复杂的图形,都是由基本图形通过变化得到的,它和基本图形有很多类似的条件和结论,类比基本图形,可以解决复杂图形的问题.
第1章
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.下列每组中的两个图形,是全等图形的是 ( )
( http: / / www.21cnjy.com )
【解析】选C.把握全等图形的定义,形状和大小完全相同的两个图形全等,与图形的位置无关.
2.如图所示的是已知∠BAC,求作∠EDF的作图痕迹,则下列说法正确的是( )
( http: / / www.21cnjy.com )
A.因为边的长度对角的大小无影响,所以BC弧的半径长度可以任意选取
B.因为边的长度对角的大小无影响,所以DE弧的半径长度可以任意选取
C.因为边的长度对角的大小无影响,所以FE弧的半径长度可以任意选取
D.以上三种说法都正确
【解析】选A.因为已知∠BAC,求作∠EDF的作图痕迹,所以边的长度对角的大小无影响,得出BC弧的半径长度可以任意选取.
3.如图,△ABC≌△ADE,已知在△ABC中,AB边最长,BC边最短,则△ADE中三边的大小关系是 ( )
( http: / / www.21cnjy.com )
A.AD=AE=DE B.AD
( http: / / www.21cnjy.com )
A.DC B.BC
C.AB D.AE+AC
【解析】选C.因为∠DAC=∠E+∠3=∠1+∠BAC,
∠1=∠3,所以∠BAC=∠E.
又因为∠2=∠3,所以∠2+∠DCA=∠3+∠DCA,
即∠BCA=∠DCE.
又因为AC=CE,所以△ABC≌△EDC,
所以DE=AB.
5.如图,工人师傅做了一个长方形窗框ABC ( http: / / www.21cnjy.com )D,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在 ( )
( http: / / www.21cnjy.com )
A.A,C两点之间 B.E,G两点之间
C.B,F两点之间 D.G,H两点之间
【解析】选B.工人师傅做了一个长方形窗框A ( http: / / www.21cnjy.com )BCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E,G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
6.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 ( )
( http: / / www.21cnjy.com )
A.50 B.62 C.65 D.68
【解析】选A.因为AE⊥AB且AE=AB,EF⊥FH,BG⊥FH,所以∠EAB=∠EFA=∠BGA=
90°,∠EAF+∠BAG=90°,∠ABG+∠BAG=90° ∠EAF=∠ABG.因为AE=AB,∠EFA=∠AGB,∠EAF=∠ABG,所以△EFA≌△AGB,所以AF=BG,AG=EF.同理,证得△BGC≌△CHD,得GC=DH,CH=BG.所以FH=FA+AG+GC+CH=3+6+4+3=16,所以S=(6+4)×16-3×4-6×3=50.
7.如图所示,在△ABC中 ( http: / / www.21cnjy.com ),AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,已知EH=EB=3,AE=4,则CH的长是 ( )
( http: / / www.21cnjy.com )
A.1 B.2
C.3 D.4
【解析】选A.因为AD⊥BC,CE⊥AB,
所以∠ADB=∠CEB=90°,
所以∠BAD+∠B=90°,∠ECB+∠B=90°.
所以∠BAD=∠ECB,
在△AEH和△CEB中,
所以△AEH≌△CEB,所以CE=AE=4,
又因为EH=3,所以CH=1.
二、填空题(每小题5分,共25分)
8.如图所示的图案是由全等的图形拼成的,其中AD=0.5cm,BC=1cm,则AF=
cm.
( http: / / www.21cnjy.com )
【解析】由题可知,图中有8个全等的梯形,所以AF=4AD+4BC=4×0.5+4×1=6(cm).
答案:6
9.如图所示,AD,BC相交于点O,△AOB≌△DOC,A,D为对应顶点,则∠C的度数为 .
( http: / / www.21cnjy.com )
【解析】因为△AOB≌△DOC,A,D为对应顶点,所以∠C=∠B,由图知∠B=30°,所以∠C的度数为30°.
答案:30°
【互动探究】如图所示,AD,BC相交于点O,∠A=∠D,AO=DO,则∠C的度数为 .
( http: / / www.21cnjy.com )
【解析】因为∠A=∠D,AO=DO,∠AOB=∠DOC,所以△AOB≌△DOC(ASA),B,C为对应顶点,所以∠C=∠B,
由图知∠B=30°,所以∠C的度数为30°.
答案:30°
10.(2013·天津中考)如图,已知 ( http: / / www.21cnjy.com )∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,请写出图中一组相等的线段 .
( http: / / www.21cnjy.com )
【解析】因为∠C=∠D,∠ABC= ( http: / / www.21cnjy.com )∠BAD,AB=BA,所以△ADB≌△BCA,所以AC=BD,BC=AD,又∠DOA=∠COB,所以△ADO≌△BCO,所以OA=OB,OC=OD.
答案:AC=BD(或BC=AD或OD=OC或OA=OB,答案不唯一)
【变式训练】如图为八个全等的正六边形紧密排列在同一平面上的情形.根据图中标示的各点位置,判断△ACD与下列哪一个三角形全等 ( )
( http: / / www.21cnjy.com )
A.△ACF B.△ADE
C.△ABC D.△BCF
【解析】选B.根据图象可知△ACD和△ADE全等,理由是:因为根据图形可知AD=AD,AE=AC,DE=DC,所以△ACD≌△AED.
11.如图,∠DAB=∠EAC=6 ( http: / / www.21cnjy.com )0°,AB=AD,AC=AE,BE和CD相交于点O,AB和CD相交于P,AC和BE相交于F,则∠DOE的度数是 .
( http: / / www.21cnjy.com )
【解析】因为∠DAB=∠EAC=60°,
所以∠DAB+∠BAC=∠BAC+∠EAC,
所以∠DAC=∠EAB,
在△ADC和△ABE中,
所以△ADC≌△ABE(SAS),所以∠E=∠ACD.
又因为∠AFE=∠OFC,所以∠COF=∠EAF=60°,
所以∠DOE=120°.
答案:120°
12.如图,点E,F分别在∠CAB的边AC,AB上,若AB=AC,AE=AF,BE与CF交于点D,给出结论:
①△ABE≌△ACF;②BD=DE;
③△BDF≌△CDE;④点D在∠BAC的平分线上.
其中正确的结论有 (填写序号).
( http: / / www.21cnjy.com )
【解析】在△CAF和△BAE中,
因为
所以△CAF≌△BAE(SAS),
即△ABE≌△ACF,所以①正确;
根据已知条件不能推出BD=DE,所以②错误;
因为△ABE≌△ACF,所以∠C=∠B.
因为AC=AB,AE=AF,所以CE=BF.
又因为∠CDE=∠BDF,所以△CDE≌△BDF(AAS),所以③正确;
如图,连接AD.
因为△CDE≌△BDF,
所以DE=DF.
因为AE=AF,AD=AD,
所以△EAD≌△FAD(SSS).
所以∠EAD=∠FAD,
即点D在∠BAC的平分线上,
所以④正确.
答案:①③④
三、解答题(共47分)
13.(10分)如图,△ABC≌△ADE,∠CAD=10°,∠B=∠D=25°,∠EAB=120°,试求∠ACB的度数.
( http: / / www.21cnjy.com )
【解析】因为△ABC≌△ADE,所以∠CAB ( http: / / www.21cnjy.com )=∠EAD.因为∠EAB=120°,∠CAD=10°,所以∠EAB=∠EAD+∠CAD+∠CAB=2∠CAB+10°=120°,所以∠CAB=55°.因为
∠B=∠D=25°,所以∠ACB=180°-∠CAB-∠B=180°-55°-25°=100°.
14.(12分)(2014·宁德质检)如图,点A,D,B,E在同一条直线上,AC=DF,AD=BE.AC∥DF.
( http: / / www.21cnjy.com )
试说明:BC=EF.
【解析】因为AC∥DF,
所以∠A=∠FDE,
又因为AD=BE,所以AB=DE,
在△ABC和△DEF中
所以△ABC≌△DEF,所以BC=EF.
15.(12分)(2014·张家口一模)如图,已知△ABC中,∠ABC=45°,AD是BC边上的高,
( http: / / www.21cnjy.com )
(1)尺规作图:在∠ABC的内部作∠CBM,使得∠CBM=∠DAC(要求:只保留作图痕迹,不写作法和理由).
(2)若射线BM与AC交于点E,与AD交于点F,且CD=3,试求线段DF的长.
【解析】(1)作图如图1:
( http: / / www.21cnjy.com )
(2)如图2:
( http: / / www.21cnjy.com )
因为AD⊥BC,∠ABC=45°,
所以∠1=∠ABC=45°,所以AD=BD.
在△BDF和△ADC中,
所以
所以△BDF≌△ADC(ASA),
所以DF=DC=3.
16.(13分)如图所示, ( http: / / www.21cnjy.com )甲、乙二人同时从O点以相同的速度出发,甲沿正东方向前进,乙沿东北方向前进,到某一时刻他们同时改变方向,甲沿正北方向前进,乙沿东南方向前进,他们的速度均保持不变,问他们相遇时在出发点的什么方向
( http: / / www.21cnjy.com )
【解析】连接OC,由题意知,OA=OB,AC=BC.
在△OAC和△OBC中,
所以△OAC≌△OBC(SSS),所以∠AOC=∠BOC.
又∠AOB=45°,所以∠AOC=∠BOC=∠AOB=22.5°,所以∠MOC=45°+22.5°=67.5°,即他们相遇时在出发点的北偏东67.5°方向上.
( http: / / www.21cnjy.com )
【知识归纳】解图形运动问题的思路
对于几何图形的运动问题以 ( http: / / www.21cnjy.com )及一些规律探究题,常常会出现一个基本图形,无论从图形上还是从解题方法上都比较简单,而其他的较复杂的图形,都是由基本图形通过变化得到的,它和基本图形有很多类似的条件和结论,类比基本图形,可以解决复杂图形的问题.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
