8.2 力的平衡(第1课时)课件
图片预览






文档简介
(共15张PPT)
第八章 力与运动
8.2 力的平衡
第1课时 力的合成
一台拖拉机能把汽车从泥泞中拉出来,但用人推,要很多人共同努力才行,说明拖拉机和人对汽车的 相同。
作用效果
课堂引入
两个小孩才能提起的一桶水,一个大人就能提起。说明两个小孩提起一桶水和一个大人提起同一桶水的 相同。
如果一个力对物体的作用效果与几个力同时对物体的作用效果相同,那么这个力就叫做那几个力的合力,那几个力就叫做这个力的分力。
作用效果
课堂引入
注意:
1.合力是“等效力”,不是物体新受到的另外一个力。
2.分析物体受力情况时,合力和分力不是同时存在的。
3.几个分力必须同时作用在同一物体上,即共点力。
等效替代法
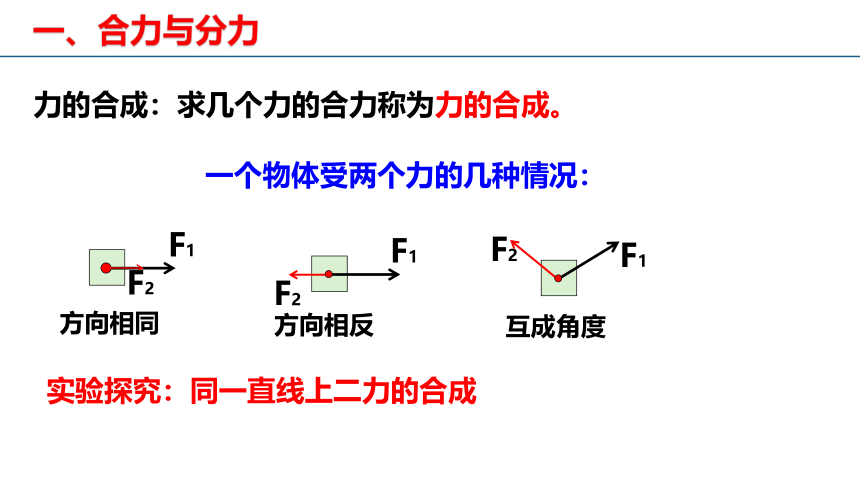
一、合力与分力
力的合成:求几个力的合力称为力的合成。
一个物体受两个力的几种情况:
F1
F2
方向相同
F1
F2
方向相反
F1
F2
互成角度
实验探究:同一直线上二力的合成
一、合力与分力
二、同一直线上的力的合成
实验方法:等效替代法
1.如果方向相同,合力大小等于两个力的大小之和,即F合=F1﹢F2,
合力方向与两力方向相同。
2.若方向相反,合力大小等于两个力的大小之差,即F =|F1-F2|,合力方向与较大力的方向相同。
二、同一直线上的力的合成
【例题1】同一直线上二力合成。
一个物体受到如图所示的两个力的作用,
F推=5N
F拉=7N
则这两个力的合力的大小为 ,方向向 。
12N
右
F合=12N
二、同一直线上的力的合成
典型例题
同一直线上的多力合成:先将同方向上的力合成,
再与不同方向上的力合成。
合力的大小为 ,方向向 。
典型例题
二、同一直线上的力的合成
1N
左
【例题2】同一直线上多力合成。
【例3】用水平向左的力F1=10N,F2=20N,F3=30N,F4=40N,水平向右的力F5=20N,F6=15N,F7=15N,F8=20N,作用在同一物体上,那么,这八个力的合力为多少,方向如何?
解:左边合力为:
F左=F1+F2+F3+F4=10N+20N+30N+40N=100N
右边合力为:
F右=F5+F6+F7+F8=20N+15N+15N+20N=70N
F合= F左-F右=100N-70N=30N
方向:水平向左
典型例题
二、同一直线上的力的合成
【例题4】一个小球的重力为5N,在空中受到0.5N的空气阻力(假设不变)
(1)竖直下落时小球受到的合力为多少?方向如何?
(1)竖直上升时小球受到的合力为多少?方向如何?
f=0.5N
G=5N
解:F合=G-f
=5N-0.5N
=4.5N
合力的方向竖直向下。
f=0.5N
G=5N
解:F合=G+f
=5N+0.5N
=5.5N
合力的方向竖直向下。
典型例题
二、同一直线上的力的合成:知分力求合力
【例题5】已知一个物体受到同一直线两个力作用的合力F合=20N,其中一个分力F1=30N,方向向左,则另一个分力F2的方向和大小分别是?
F1=30N
F2=10N
F1=30N
F2=50N
典型例题
二、同一直线上的力的合成:知合力求分力
【例题6】小杨用80N的水平力推着箱子向右匀速前进,突然发现前面有台阶,他马上用20N的水平力向后拉箱子,使其减速,则箱子在减速过程中受到的合力为_________N
F=80N
f=80N
F=20N
f=80N
100
典型例题
二、同一直线上的力的合成
拔河比赛
赛龙舟比赛
三、力的合成的应用
课堂小结
一、合力与分力
二、同一直线上的力的合成
1.同一直线上二力合成。
2.同一直线上多力合成。
3.知分力求合力、知合力求分力
力的合成
第八章 力与运动
8.2 力的平衡
第1课时 力的合成
一台拖拉机能把汽车从泥泞中拉出来,但用人推,要很多人共同努力才行,说明拖拉机和人对汽车的 相同。
作用效果
课堂引入
两个小孩才能提起的一桶水,一个大人就能提起。说明两个小孩提起一桶水和一个大人提起同一桶水的 相同。
如果一个力对物体的作用效果与几个力同时对物体的作用效果相同,那么这个力就叫做那几个力的合力,那几个力就叫做这个力的分力。
作用效果
课堂引入
注意:
1.合力是“等效力”,不是物体新受到的另外一个力。
2.分析物体受力情况时,合力和分力不是同时存在的。
3.几个分力必须同时作用在同一物体上,即共点力。
等效替代法
一、合力与分力
力的合成:求几个力的合力称为力的合成。
一个物体受两个力的几种情况:
F1
F2
方向相同
F1
F2
方向相反
F1
F2
互成角度
实验探究:同一直线上二力的合成
一、合力与分力
二、同一直线上的力的合成
实验方法:等效替代法
1.如果方向相同,合力大小等于两个力的大小之和,即F合=F1﹢F2,
合力方向与两力方向相同。
2.若方向相反,合力大小等于两个力的大小之差,即F =|F1-F2|,合力方向与较大力的方向相同。
二、同一直线上的力的合成
【例题1】同一直线上二力合成。
一个物体受到如图所示的两个力的作用,
F推=5N
F拉=7N
则这两个力的合力的大小为 ,方向向 。
12N
右
F合=12N
二、同一直线上的力的合成
典型例题
同一直线上的多力合成:先将同方向上的力合成,
再与不同方向上的力合成。
合力的大小为 ,方向向 。
典型例题
二、同一直线上的力的合成
1N
左
【例题2】同一直线上多力合成。
【例3】用水平向左的力F1=10N,F2=20N,F3=30N,F4=40N,水平向右的力F5=20N,F6=15N,F7=15N,F8=20N,作用在同一物体上,那么,这八个力的合力为多少,方向如何?
解:左边合力为:
F左=F1+F2+F3+F4=10N+20N+30N+40N=100N
右边合力为:
F右=F5+F6+F7+F8=20N+15N+15N+20N=70N
F合= F左-F右=100N-70N=30N
方向:水平向左
典型例题
二、同一直线上的力的合成
【例题4】一个小球的重力为5N,在空中受到0.5N的空气阻力(假设不变)
(1)竖直下落时小球受到的合力为多少?方向如何?
(1)竖直上升时小球受到的合力为多少?方向如何?
f=0.5N
G=5N
解:F合=G-f
=5N-0.5N
=4.5N
合力的方向竖直向下。
f=0.5N
G=5N
解:F合=G+f
=5N+0.5N
=5.5N
合力的方向竖直向下。
典型例题
二、同一直线上的力的合成:知分力求合力
【例题5】已知一个物体受到同一直线两个力作用的合力F合=20N,其中一个分力F1=30N,方向向左,则另一个分力F2的方向和大小分别是?
F1=30N
F2=10N
F1=30N
F2=50N
典型例题
二、同一直线上的力的合成:知合力求分力
【例题6】小杨用80N的水平力推着箱子向右匀速前进,突然发现前面有台阶,他马上用20N的水平力向后拉箱子,使其减速,则箱子在减速过程中受到的合力为_________N
F=80N
f=80N
F=20N
f=80N
100
典型例题
二、同一直线上的力的合成
拔河比赛
赛龙舟比赛
三、力的合成的应用
课堂小结
一、合力与分力
二、同一直线上的力的合成
1.同一直线上二力合成。
2.同一直线上多力合成。
3.知分力求合力、知合力求分力
力的合成
