2009初中毕业生学业考试数学试题常用解法点悟(有详细答案)
文档属性
| 名称 | 2009初中毕业生学业考试数学试题常用解法点悟(有详细答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-05 00:00:00 | ||
图片预览







文档简介
课件48张PPT。 初中毕业生学业考试
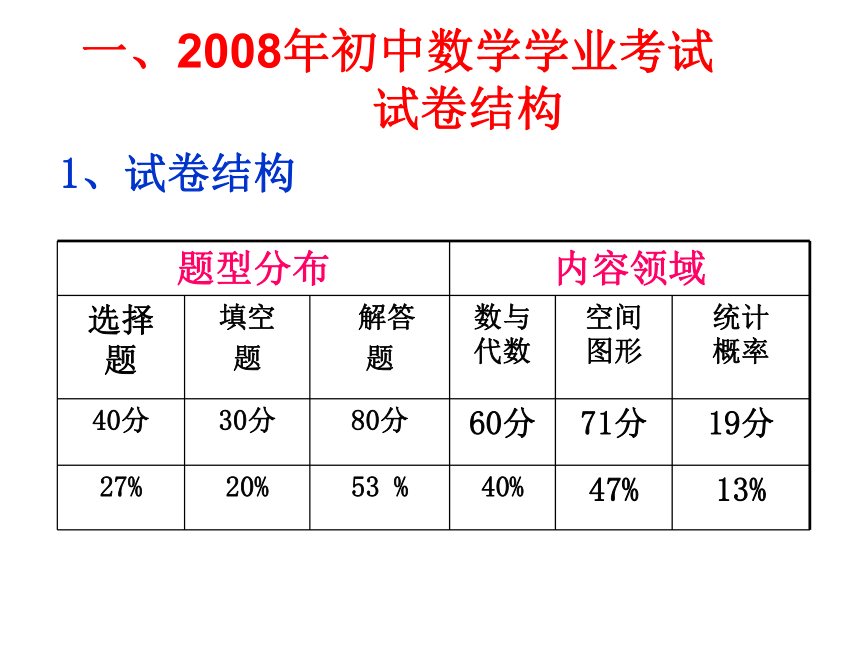
数学试题常用解法点悟一、2008年初中数学学业考试
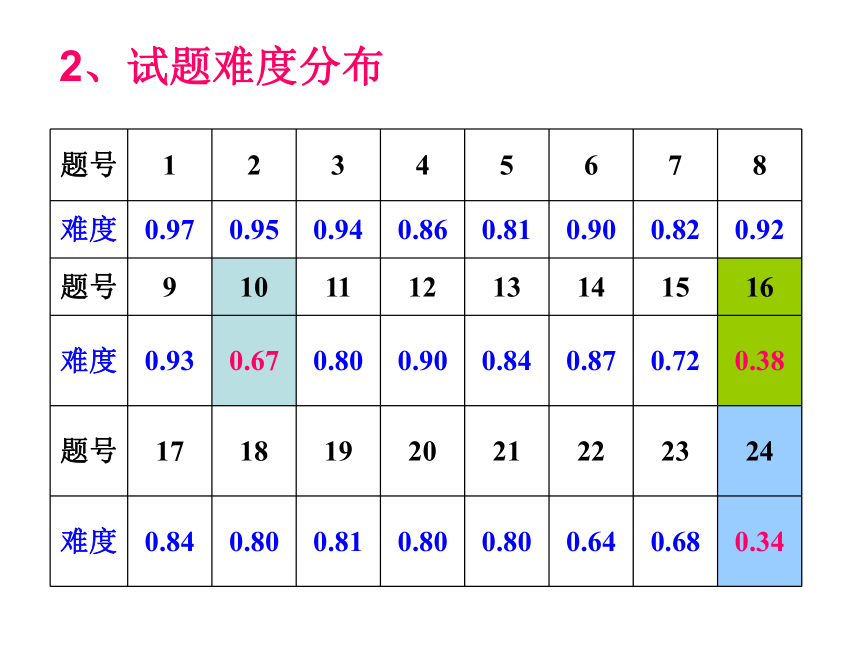
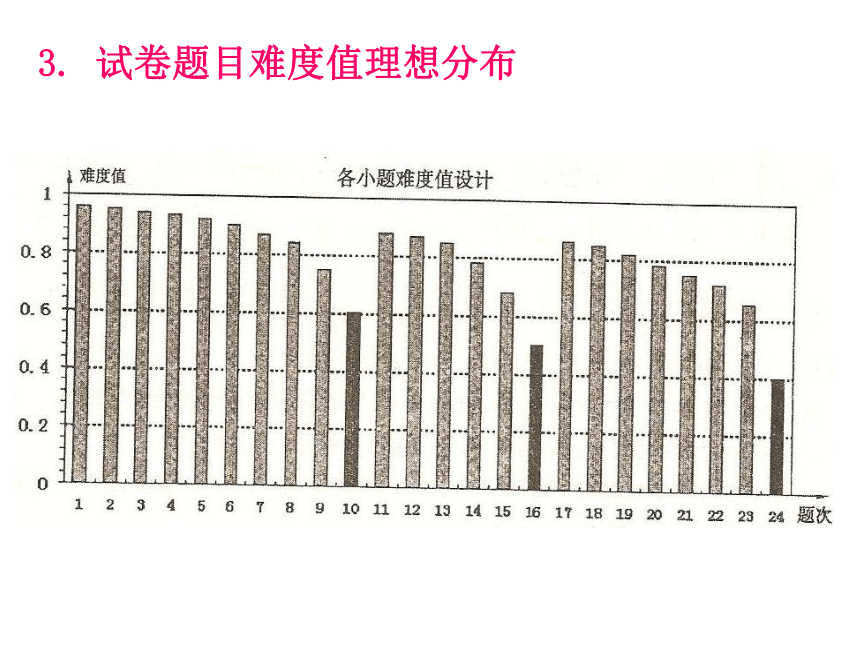
试卷结构1、试卷结构2、试题难度分布3. 试卷题目难度值理想分布二、数学学业考试试题常用解法(一)、选择题的常用解法(5)图像法(1)直接法(2)排除法(3)验证法(4)特值法 例:1、函数 中,自变量x取值范围是( )
(A)x≥-1 (B)x>2
(C)x>-1且x≠2 (D)x≥-1 且x≠2D(直接法)B把C=2b-5代入得,Y= x2 + bx +2b-5当x=-2时, Y= 4-2 b + 2b-5=-14、在同一坐标平面内,图象不可能由函数 的图象通过平移变换、轴对称变换得到的函数是( ) 3、(09瑞安模拟第3题)瑞安大桥(飞云江三桥)为独塔双索面斜拉桥,整座大桥长2956米,则桥长用科学记数法表示为(保留两个有效数字)( )
A.2.9×103米 B.30×102米
C.3.0×103米 D.29×102米(排除法)DC6、已知α满足50°<α<90°,则下列结论正确的
是 ( )
(A)tanα<cosα<sinα
(B)sinα<tanα<cosα
(C)cosα<sinα<tanα
(D)cosα<tanα<sinα(图象法)BC取α=60°(特值法)7、为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需花60元,经过协商每种钢笔单价下降1元,结果共花了48元,那么甲种钢笔可能购买了( )
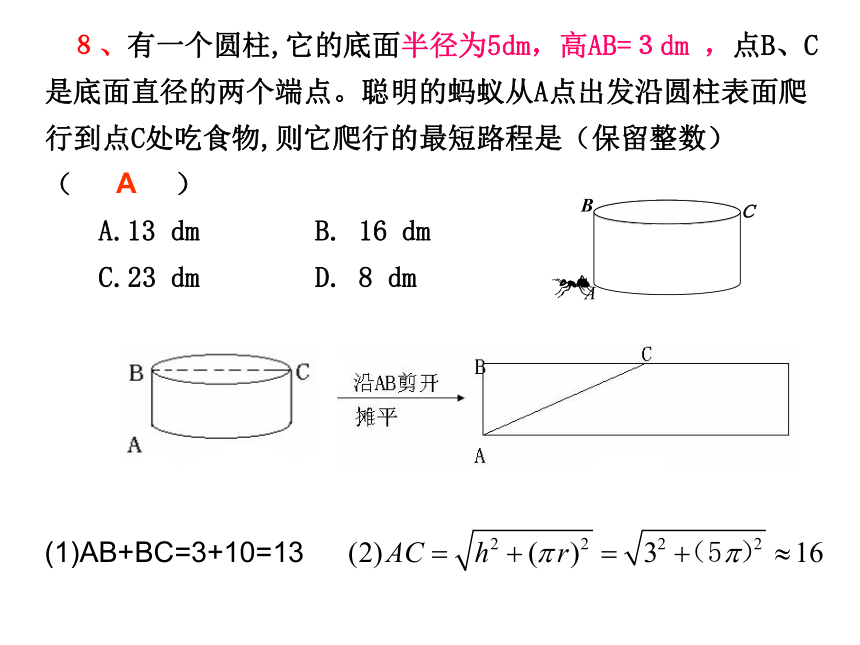
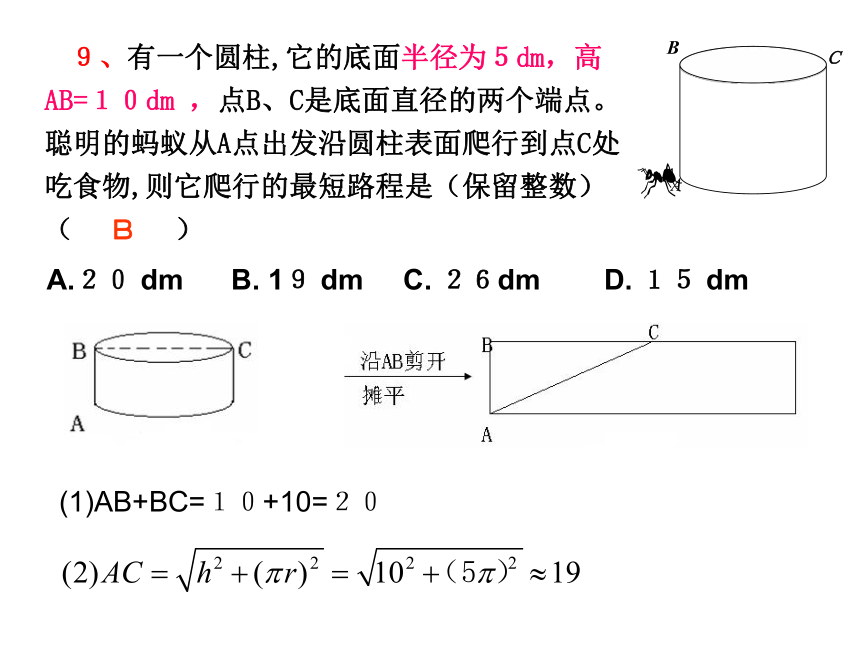
A.11支 B.9支 C.7支 D.5支 (验证法)D解:设甲、乙、丙三种钢笔分别购买 X、Y、Z 支,则有因为钢笔的支数为非负整数 ,所以选D(1)AB+BC=3+10=13A9、有一个圆柱,它的底面半径为5dm,高AB=10dm ,点B、C是底面直径的两个端点。聪明的蚂蚁从A点出发沿圆柱表面爬行到点C处吃食物,则它爬行的最短路程是(保留整数)( )(1)AB+BC=10+10=20BA.20 dm B. 19 dm C. 26dm D. 15 dm (二)、填空题的解法(6)注意挖掘隐含条件(1)是否需分类讨论(2)是否有出现漏解(3)是否有思维定势(4)有无结果需舍去(5)结果是否需还原 (注意分类)2、在半径为1的⊙中,弦 则∠CAB= ; 例1、三角形的每条边的长都是方程X2-8X+15=0
的根,则三角形的周长是 ; 3、5、5或3、3、513或1115°或75° 3、如图,在由24个边长都为1的小正三角形组成的网格中,点P是正六边形的一个顶点,以点P为直角顶点作直角三角形(即顶点
均在格点上的三角形),请你
写出所有可能的直角三角形斜
边长为 。(不经过第二象限,可以是经过第1、3、4象限或经过原点的1、3象限) 4、若一次函数 的图像不经过第二象限,则K的取值范围 .K>0,K-1≤0,∴0<K≤10<K≤1(不能思维定势)(不能漏解)5、已知一元二次方程
的一根为0,则a= . -1(结果需舍去) 6、 (09瑞安模拟第14题)反比例函数的图象如图所示,点M是该函数图象上一点, MN垂直于x轴,垂足是点N,如果S△MON=2,则k的 值为 . K=-47、“五.一”节公园举办游圆活动,一开始有(50a-40)位游客参加,活动进行至一半,有(45-20a)位游客因有事中途退场,则开始参加时有 位游客。 挖掘条件:(1)a为正整数(2) (50a-40)>0, a>(3)(45-20a)>0, a<(4) (50a-40)> (45-20a),70 a>85, a>∴ a=2 50a-40=6060练习:1、如图1,是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm)。将它们拼成如图2的新几何体, 则该新几何体的体积为( )
A.48πcm3 B.60πcm3 C.72πcm3 D.84πcm32、如图,在△ABC中,∠C=90°,点A关于
直线BC的对称点为,点B关于直线CA的对称
点为,点C关于直线AB的对称点为。若△ABC
的面积为S,那么△的面积是 .D1、如图1,是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm)。将它们拼成如图2的新几何体, 则该新几何体的体积为( )
A.48πcm3 B.60πcm3 C.72πcm3 D.84πcm3B2、如图,在△ABC中,∠C=90°,点A关于直线BC的对称点为,点B关于直线CA的对称点为,点C关于直线AB的对称点为。若△ABC的面积为S,那么△的面积是 .解:延长C′C交A′B′于点D′D则C′D′=3CD3S3、矩形ABCD中,AB=3,BC=6,AE=CH=1,AF=CG=2,点P是EF、GH所在直线内部任意一点,则△PEF与△PGH的面积为 ▲ . (三)、解答题的解法 (1) 格式规范,步骤合理,
过程详细,步步有据。在解答这类题时,应注意以下几点:1、基础题(常规题)(基本概念、法则不清)(缺少必要的过程和步骤)2、作图题2000年—2005年温州卷:图形分割(等积思想)
2006年—2008年温州卷:图形变换(全等变换)(1)尺规作图(用直尺和圆规作线、角、三角
形、四边 形、圆等)
(2)镶嵌平面(拼接图形)
(3)图形割拚(先分割,再拼接) (09年瑞安模拟第20题)请你用直尺和圆规,用三种不同的方法画一个角等于直角(不写作法和证明,但要保留作图痕迹,并标出或写出直角).(1)尺规作图———用没有刻度的直尺和圆规作
图,简称尺规作图。(2)镶嵌平面——拼成一个无缝隙、不重叠的平面图形。思考:用正多边形镶嵌平面,需要满足什么条件?条件:①正多边形的边长都相等;
②顶点的各个角之和为360°。原理:方程思想,求方程a x +b y =360的正整数解. 我们知道,能单独镶嵌平面的正多边只有三种,即正三角形、正方形、正六边形。请你选择其中两种正多边形,用三种不同的镶嵌方式使它们能镶嵌平面,画出你选择的两种正多边形镶嵌平面的图形(只要求画出示意图).①正三角形和正方形. 如果用x个正三角形、y个正方形进行平面密铺,可得600×x+900×y=3600,化简得2x+3y=12。因为x、y都是正整数,所以只有当x=3,y=2②正三角形和正六边形③正方形和正六边形 如果用x个正三角形、y个正六边形进行平面密铺,可得600×x+1200×y=3600,化简得x+2y=6。因为x、y都是正整数,所以只有当x=2,y=2.或x=4,y=1. 如果用x个正方形、y个正六边形进行平面密铺,可得900×x+1200×y=3600,化简得3x+4y=12。因为x、y都是正整数,所以方程无解. 课外作业:正三角形与正十二边形镶嵌平面;正四边形与正八边形镶嵌平面;正五边形与正十边形镶嵌平面;尝试用三种或更多种正多边形能否镶嵌平面?(3)图形割拚(先分割,再拼接。等积思想)
现有①、②、③、④、⑤五个图形(如图所示),请你设计三种不同的拚接方案,把下列的五个图形都用上且只用一次,分别拚成一个直角三角形,一个梯形,一个正方形。一个直角三角形一个梯形一个正方形 (2)仔细审题,注意答题技巧,掌握解题策略,做到化繁为简,化生为熟。 波利亚说:“解题的成功要靠正确思路的选择,要靠从可以接近它的方向攻击堡垒。” 3、应用题问题解决的基本步骤是:
(1)理解问题(审题、信息输入)
(2)制订计划(分析、信息加工)
(3)执行计划(建模、信息输出)
(4)回顾反思(检验)例1、随着经济的发展,对各类人才的需求也不断增加。现温州某公司要招聘操作工和包装工两工种的人员共150人,且操作工的人数不少于包装工人数的2倍,工资待遇分别是操作工每人每月1000元,包装工每人每月600元。
(1)问:操作工和包装工各招聘多少人时,可使公司每月所付的基本工资总额最少,此时最少工资总额是多少?
(2)在保证这两工种基本工资总额最少的条件下,根据工作表现出色,公司领导决定另用10万元奖励他们,其中包装工人均奖金不得超过操作工的人均奖金,但不低于200元,若以百元单位发放奖金,问:在人均奖金上有几种奖励方案?把它们写出来。(1)理解问题已知未知①操作工和包装工共150人②操作工的人数不少于包装工人数的2倍,③操作工、包装工每人每月分别1000元、600元。①操作工和包装工各多少人时,每月的工资总额最少?②最少工资总额是多少?③10万元奖金,包装工人均奖金不得超过操作工的人均奖金,但不低于200元,有几种奖励方案?(2)制订计划①操作工和包装工各多少人时,每月的工资总额
最少?最少工资总额是多少?②10万元奖金,包装工人均奖金不得超过操作工的人均奖金,但不低于200元,有几种奖励方案? 根据题意,先列出工资总额关于人数的函数关系式,然后利用函数性质求解。建立方程和不等式求整数解,写出奖励方案。(3)执行计划解:(1)设招聘包装工x人,基本工资总额为y元,根据题意得:∴相应的a分别为600,400,200.∴有三种方案:
方案1:人均奖金包装工人为600元,操作工为700元;
方案2: 人均奖金包装工人为400元, 操作工为 800元; 方案3:人均奖金包装工人为 200元, 操作工为 900元;(4)回顾反思:解决实际问题的基本思想方法例2、如图,正方形木板ABCD的边长为4cm,在对称中心O处有一钉子,动点P、Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止;点Q沿A→D方向以每秒1cm的速度运动,到点D停止。P、Q两点用一条可伸缩的细橡皮筋联结,设x秒后橡皮筋扫过的面积为Ycm2
(1)当x为何值时,橡皮筋刚好
触及钉子;
(2)求Y与x之间的函数关系式.
(3)是否存在x的值,使△POQ为
直角三角形?不存在的,试说
明理由;存在的,请求出x的值.(1)当x为何值时,橡皮筋刚好触及钉子;①②③(2)求Y与x之间的函数关系式.①(3)是否存在x的值,使△POQ为直角三角形?不存在的,试说明理由;存在的,请求出x的值.②
③综上所述,存在X的值,
或 或 △POQ是
直角三角形 存在性探索型问题解题方法是:先假设数学对象存在或成立,以此为前提进行运算或推理。若推出矛盾,否定假设;否则给出肯定的证明。 动态几何问题的解题策略是:化动为静、动中求静,依据题设,寻求动点在运动过程的特殊位置或特殊时刻,综合运用数形结合、函数与方程、分类讨论等思想方法解决问题。 分类讨论等思想:把一个复杂的数学问题分成若干个属性不同的情况逐一讨论研究,以获得完整的结果。其步骤是:首先确定讨论的对象和范围,其次确定分类的标准,然后逐级讨论并总结出结论。总结与反思 2、扎实基础知识, 学会思想方法3、注重知识联系,加强思维训练4、学会数学建模,增强应用意识五、注意事项及建议1、领会《考试说明》,明 确 具 体要 求5、提高分析能力 ,重视问题探究6、学习“例卷答案”,了解“评分标准”12、仔细审题,详细答题,格式规范,卷面整洁。7、拿到试卷后,不忙答题,先对试卷整体感知;8、准确填写姓名和准考证号,并与条码核准;9、选择题必须用2B铅笔填涂,非选择题必须用
0.5 毫米及以上的黑色签字笔书写在;10、严格按题号顺序在答题纸相应答题区域作答,
否则无效;11、作图先用铅笔画好,然后用黑色签字笔重描;我易人易,我不大意;我难人难,我不畏难. 祝同学们2009年学业考试
取 得 优异 成 绩谢谢,再见!
数学试题常用解法点悟一、2008年初中数学学业考试
试卷结构1、试卷结构2、试题难度分布3. 试卷题目难度值理想分布二、数学学业考试试题常用解法(一)、选择题的常用解法(5)图像法(1)直接法(2)排除法(3)验证法(4)特值法 例:1、函数 中,自变量x取值范围是( )
(A)x≥-1 (B)x>2
(C)x>-1且x≠2 (D)x≥-1 且x≠2D(直接法)B把C=2b-5代入得,Y= x2 + bx +2b-5当x=-2时, Y= 4-2 b + 2b-5=-14、在同一坐标平面内,图象不可能由函数 的图象通过平移变换、轴对称变换得到的函数是( ) 3、(09瑞安模拟第3题)瑞安大桥(飞云江三桥)为独塔双索面斜拉桥,整座大桥长2956米,则桥长用科学记数法表示为(保留两个有效数字)( )
A.2.9×103米 B.30×102米
C.3.0×103米 D.29×102米(排除法)DC6、已知α满足50°<α<90°,则下列结论正确的
是 ( )
(A)tanα<cosα<sinα
(B)sinα<tanα<cosα
(C)cosα<sinα<tanα
(D)cosα<tanα<sinα(图象法)BC取α=60°(特值法)7、为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需花60元,经过协商每种钢笔单价下降1元,结果共花了48元,那么甲种钢笔可能购买了( )
A.11支 B.9支 C.7支 D.5支 (验证法)D解:设甲、乙、丙三种钢笔分别购买 X、Y、Z 支,则有因为钢笔的支数为非负整数 ,所以选D(1)AB+BC=3+10=13A9、有一个圆柱,它的底面半径为5dm,高AB=10dm ,点B、C是底面直径的两个端点。聪明的蚂蚁从A点出发沿圆柱表面爬行到点C处吃食物,则它爬行的最短路程是(保留整数)( )(1)AB+BC=10+10=20BA.20 dm B. 19 dm C. 26dm D. 15 dm (二)、填空题的解法(6)注意挖掘隐含条件(1)是否需分类讨论(2)是否有出现漏解(3)是否有思维定势(4)有无结果需舍去(5)结果是否需还原 (注意分类)2、在半径为1的⊙中,弦 则∠CAB= ; 例1、三角形的每条边的长都是方程X2-8X+15=0
的根,则三角形的周长是 ; 3、5、5或3、3、513或1115°或75° 3、如图,在由24个边长都为1的小正三角形组成的网格中,点P是正六边形的一个顶点,以点P为直角顶点作直角三角形(即顶点
均在格点上的三角形),请你
写出所有可能的直角三角形斜
边长为 。(不经过第二象限,可以是经过第1、3、4象限或经过原点的1、3象限) 4、若一次函数 的图像不经过第二象限,则K的取值范围 .K>0,K-1≤0,∴0<K≤10<K≤1(不能思维定势)(不能漏解)5、已知一元二次方程
的一根为0,则a= . -1(结果需舍去) 6、 (09瑞安模拟第14题)反比例函数的图象如图所示,点M是该函数图象上一点, MN垂直于x轴,垂足是点N,如果S△MON=2,则k的 值为 . K=-47、“五.一”节公园举办游圆活动,一开始有(50a-40)位游客参加,活动进行至一半,有(45-20a)位游客因有事中途退场,则开始参加时有 位游客。 挖掘条件:(1)a为正整数(2) (50a-40)>0, a>(3)(45-20a)>0, a<(4) (50a-40)> (45-20a),70 a>85, a>∴ a=2 50a-40=6060练习:1、如图1,是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm)。将它们拼成如图2的新几何体, 则该新几何体的体积为( )
A.48πcm3 B.60πcm3 C.72πcm3 D.84πcm32、如图,在△ABC中,∠C=90°,点A关于
直线BC的对称点为,点B关于直线CA的对称
点为,点C关于直线AB的对称点为。若△ABC
的面积为S,那么△的面积是 .D1、如图1,是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm)。将它们拼成如图2的新几何体, 则该新几何体的体积为( )
A.48πcm3 B.60πcm3 C.72πcm3 D.84πcm3B2、如图,在△ABC中,∠C=90°,点A关于直线BC的对称点为,点B关于直线CA的对称点为,点C关于直线AB的对称点为。若△ABC的面积为S,那么△的面积是 .解:延长C′C交A′B′于点D′D则C′D′=3CD3S3、矩形ABCD中,AB=3,BC=6,AE=CH=1,AF=CG=2,点P是EF、GH所在直线内部任意一点,则△PEF与△PGH的面积为 ▲ . (三)、解答题的解法 (1) 格式规范,步骤合理,
过程详细,步步有据。在解答这类题时,应注意以下几点:1、基础题(常规题)(基本概念、法则不清)(缺少必要的过程和步骤)2、作图题2000年—2005年温州卷:图形分割(等积思想)
2006年—2008年温州卷:图形变换(全等变换)(1)尺规作图(用直尺和圆规作线、角、三角
形、四边 形、圆等)
(2)镶嵌平面(拼接图形)
(3)图形割拚(先分割,再拼接) (09年瑞安模拟第20题)请你用直尺和圆规,用三种不同的方法画一个角等于直角(不写作法和证明,但要保留作图痕迹,并标出或写出直角).(1)尺规作图———用没有刻度的直尺和圆规作
图,简称尺规作图。(2)镶嵌平面——拼成一个无缝隙、不重叠的平面图形。思考:用正多边形镶嵌平面,需要满足什么条件?条件:①正多边形的边长都相等;
②顶点的各个角之和为360°。原理:方程思想,求方程a x +b y =360的正整数解. 我们知道,能单独镶嵌平面的正多边只有三种,即正三角形、正方形、正六边形。请你选择其中两种正多边形,用三种不同的镶嵌方式使它们能镶嵌平面,画出你选择的两种正多边形镶嵌平面的图形(只要求画出示意图).①正三角形和正方形. 如果用x个正三角形、y个正方形进行平面密铺,可得600×x+900×y=3600,化简得2x+3y=12。因为x、y都是正整数,所以只有当x=3,y=2②正三角形和正六边形③正方形和正六边形 如果用x个正三角形、y个正六边形进行平面密铺,可得600×x+1200×y=3600,化简得x+2y=6。因为x、y都是正整数,所以只有当x=2,y=2.或x=4,y=1. 如果用x个正方形、y个正六边形进行平面密铺,可得900×x+1200×y=3600,化简得3x+4y=12。因为x、y都是正整数,所以方程无解. 课外作业:正三角形与正十二边形镶嵌平面;正四边形与正八边形镶嵌平面;正五边形与正十边形镶嵌平面;尝试用三种或更多种正多边形能否镶嵌平面?(3)图形割拚(先分割,再拼接。等积思想)
现有①、②、③、④、⑤五个图形(如图所示),请你设计三种不同的拚接方案,把下列的五个图形都用上且只用一次,分别拚成一个直角三角形,一个梯形,一个正方形。一个直角三角形一个梯形一个正方形 (2)仔细审题,注意答题技巧,掌握解题策略,做到化繁为简,化生为熟。 波利亚说:“解题的成功要靠正确思路的选择,要靠从可以接近它的方向攻击堡垒。” 3、应用题问题解决的基本步骤是:
(1)理解问题(审题、信息输入)
(2)制订计划(分析、信息加工)
(3)执行计划(建模、信息输出)
(4)回顾反思(检验)例1、随着经济的发展,对各类人才的需求也不断增加。现温州某公司要招聘操作工和包装工两工种的人员共150人,且操作工的人数不少于包装工人数的2倍,工资待遇分别是操作工每人每月1000元,包装工每人每月600元。
(1)问:操作工和包装工各招聘多少人时,可使公司每月所付的基本工资总额最少,此时最少工资总额是多少?
(2)在保证这两工种基本工资总额最少的条件下,根据工作表现出色,公司领导决定另用10万元奖励他们,其中包装工人均奖金不得超过操作工的人均奖金,但不低于200元,若以百元单位发放奖金,问:在人均奖金上有几种奖励方案?把它们写出来。(1)理解问题已知未知①操作工和包装工共150人②操作工的人数不少于包装工人数的2倍,③操作工、包装工每人每月分别1000元、600元。①操作工和包装工各多少人时,每月的工资总额最少?②最少工资总额是多少?③10万元奖金,包装工人均奖金不得超过操作工的人均奖金,但不低于200元,有几种奖励方案?(2)制订计划①操作工和包装工各多少人时,每月的工资总额
最少?最少工资总额是多少?②10万元奖金,包装工人均奖金不得超过操作工的人均奖金,但不低于200元,有几种奖励方案? 根据题意,先列出工资总额关于人数的函数关系式,然后利用函数性质求解。建立方程和不等式求整数解,写出奖励方案。(3)执行计划解:(1)设招聘包装工x人,基本工资总额为y元,根据题意得:∴相应的a分别为600,400,200.∴有三种方案:
方案1:人均奖金包装工人为600元,操作工为700元;
方案2: 人均奖金包装工人为400元, 操作工为 800元; 方案3:人均奖金包装工人为 200元, 操作工为 900元;(4)回顾反思:解决实际问题的基本思想方法例2、如图,正方形木板ABCD的边长为4cm,在对称中心O处有一钉子,动点P、Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止;点Q沿A→D方向以每秒1cm的速度运动,到点D停止。P、Q两点用一条可伸缩的细橡皮筋联结,设x秒后橡皮筋扫过的面积为Ycm2
(1)当x为何值时,橡皮筋刚好
触及钉子;
(2)求Y与x之间的函数关系式.
(3)是否存在x的值,使△POQ为
直角三角形?不存在的,试说
明理由;存在的,请求出x的值.(1)当x为何值时,橡皮筋刚好触及钉子;①②③(2)求Y与x之间的函数关系式.①(3)是否存在x的值,使△POQ为直角三角形?不存在的,试说明理由;存在的,请求出x的值.②
③综上所述,存在X的值,
或 或 △POQ是
直角三角形 存在性探索型问题解题方法是:先假设数学对象存在或成立,以此为前提进行运算或推理。若推出矛盾,否定假设;否则给出肯定的证明。 动态几何问题的解题策略是:化动为静、动中求静,依据题设,寻求动点在运动过程的特殊位置或特殊时刻,综合运用数形结合、函数与方程、分类讨论等思想方法解决问题。 分类讨论等思想:把一个复杂的数学问题分成若干个属性不同的情况逐一讨论研究,以获得完整的结果。其步骤是:首先确定讨论的对象和范围,其次确定分类的标准,然后逐级讨论并总结出结论。总结与反思 2、扎实基础知识, 学会思想方法3、注重知识联系,加强思维训练4、学会数学建模,增强应用意识五、注意事项及建议1、领会《考试说明》,明 确 具 体要 求5、提高分析能力 ,重视问题探究6、学习“例卷答案”,了解“评分标准”12、仔细审题,详细答题,格式规范,卷面整洁。7、拿到试卷后,不忙答题,先对试卷整体感知;8、准确填写姓名和准考证号,并与条码核准;9、选择题必须用2B铅笔填涂,非选择题必须用
0.5 毫米及以上的黑色签字笔书写在;10、严格按题号顺序在答题纸相应答题区域作答,
否则无效;11、作图先用铅笔画好,然后用黑色签字笔重描;我易人易,我不大意;我难人难,我不畏难. 祝同学们2009年学业考试
取 得 优异 成 绩谢谢,再见!
同课章节目录
