2023—2024学年人教版数学九年级下册第二十六单元 反比例函数复习试题(含答案)
文档属性
| 名称 | 2023—2024学年人教版数学九年级下册第二十六单元 反比例函数复习试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 511.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 16:56:26 | ||
图片预览


文档简介
第二十六单元 反比例函数 复习试题 2023—2024学年人教版数学九年级下册
一、单选题
1.已知点A(1,-3)关于x轴的对称点A'在反比例函数 的图像上,则实数k的值为( )
A.3 B. C.-3 D.
2.若反比例函数 的图象经过点(3,﹣2),则k的值为( )
A.﹣9 B.3 C.﹣6 D.9
3.反比例函数y= (x<0)的图象如图所示,随着x值的增大,y值( )
A.增大 B.减小
C.不变 D.先增大后减小
4.若点A(-2,y1),B(-1,y2)都在反比例函数y=的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
5.反比例函数y=与正比例函数y=2x一个交点为(1,2),则另一个交点是( )
A.(-1,-2) B.(-2,-1) C.(1,2) D.(2,1)
6.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y= 的图象上,则y1,y2,y3的大小关系是( )
A.y37.在同一平面直角坐标系中,反比例函数y=(k≠0)与二次函数y=x2-kx-k的大致图象是( )
A. B.
C. D.
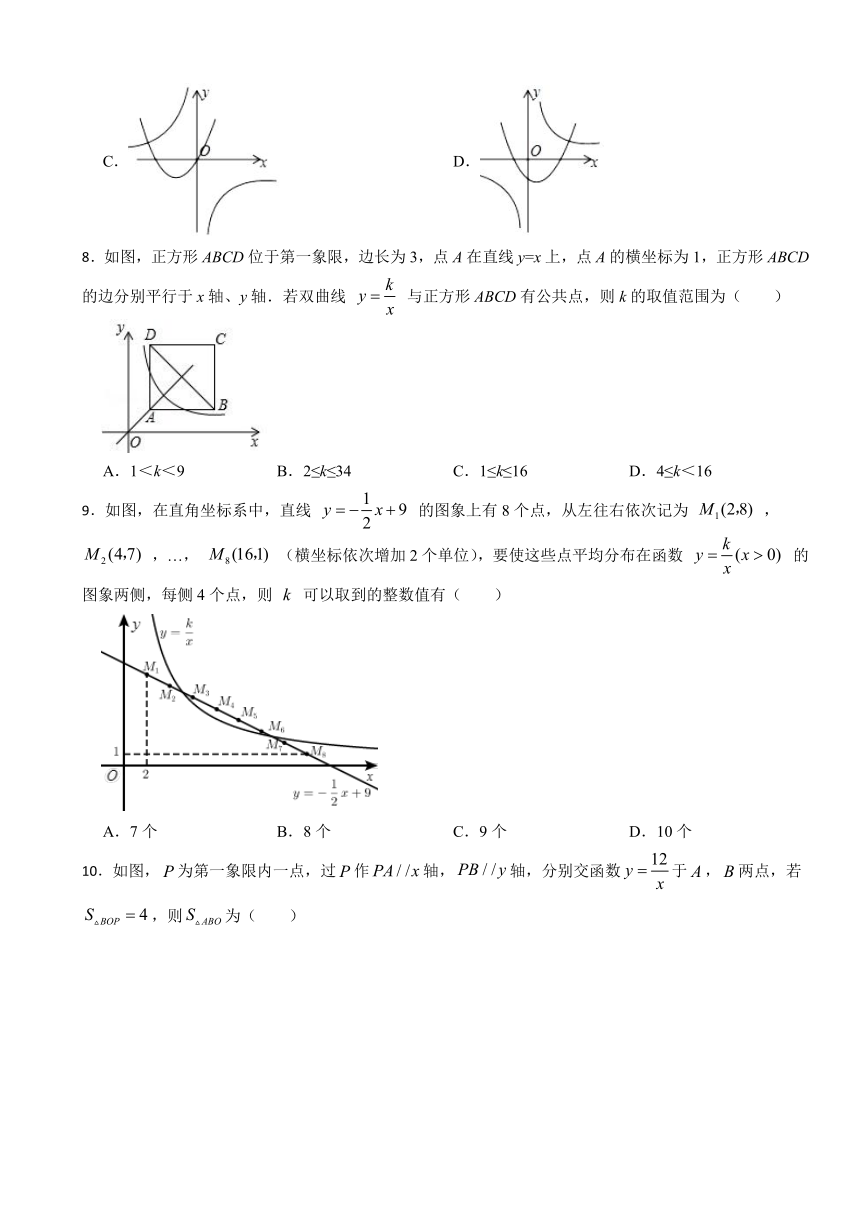
8.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
9.如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( )
A.7个 B.8个 C.9个 D.10个
10.如图,为第一象限内一点,过作轴,轴,分别交函数于,两点,若,则为( )
A.12 B.14 C.16 D.18
11.如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B(,),则k的值为( )
A.-6 B.-6 C.-12 D.-12
12.如图,在平面直角坐标系中,线段的端点点A、点D分别在y轴与x轴上.且与反比例函数交于点B、点C,且,面积为3,则k的值为( )
A. B. C. D.
二、填空题
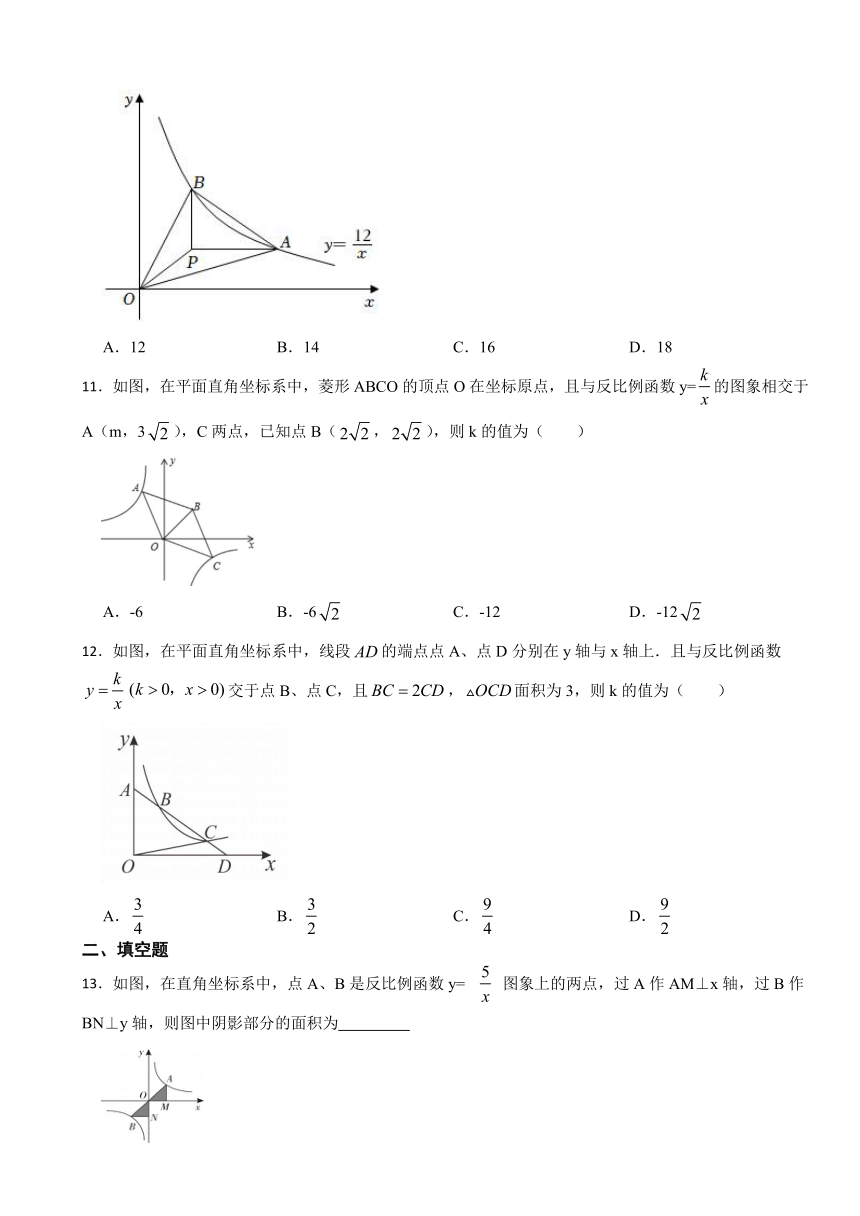
13.如图,在直角坐标系中,点A、B是反比例函数y=
图象上的两点,过A作AM⊥x轴,过B作BN⊥y轴,则图中阴影部分的面积为
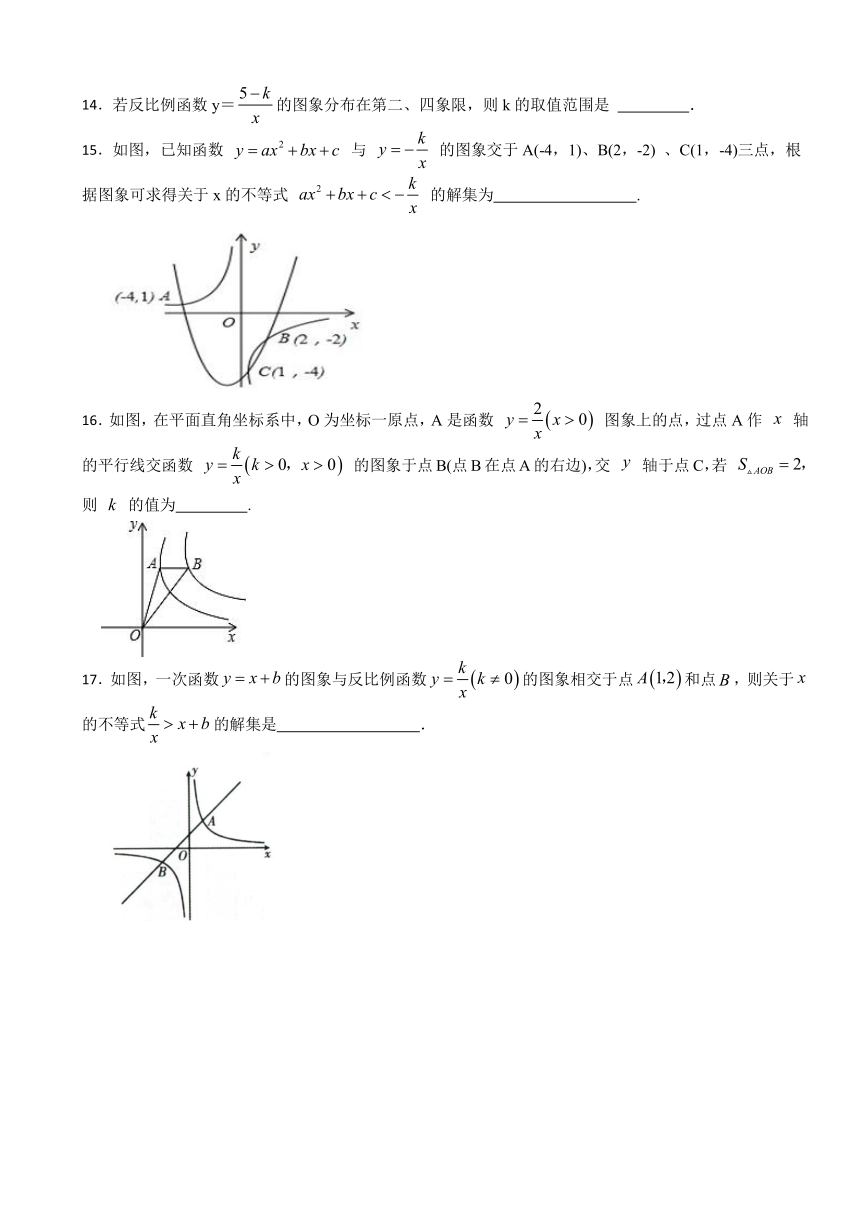
14.若反比例函数y=的图象分布在第二、四象限,则k的取值范围是 .
15.如图,已知函数 与 的图象交于A(-4,1)、B(2,-2) 、C(1,-4)三点,根据图象可求得关于x的不等式 的解集为 .
16.如图,在平面直角坐标系中,O为坐标一原点,A是函数 图象上的点,过点A作 轴的平行线交函数 的图象于点B(点B在点A的右边),交 轴于点C,若 则 的值为 .
17.如图,一次函数的图象与反比例函数的图象相交于点和点,则关于的不等式的解集是 .
三、解答题
18.如图,已知正比例函数和反比例函数的图象交于点.
(1)求反比例函数的表达式;
(2)观察图象,直接写出当时,自变量的取值范围;
(3)将直线沿轴向上平移,使平移后的直线与轴交于,与双曲线在第一象限内交于点,求点的坐标.
19.如图,已知一次函数y=2x+b的图象与反比例函数的图象相交于A,B两点,与y轴相交于点C,且点B的坐标为(-3,-1).
(1)求一次函数和反比例函数的表达式及点A的坐标.
(2)若请直接写出x的取值范围.
(3)求△AOB的面积.
20.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)求y与的函数表达式;
(2)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多长时间,才能使蔬菜避免受到伤害?
21.小明要把一篇社会调查报告录入电脑,当他以100字/分钟的速度录入文字时,经过240分钟能完成录入。设他录入文字的速度为v字/分钟时,完成录入的时间为t分钟。求t与v之间的函数关系式(不必写出自变量的取值范围)。
22.如图,一次函数的图象与反比例函数的图象交于、两点,其中点坐标为,点到轴的距离为1.
(1)试确定、的估;
(2)求点的坐标.
23.在反比例函数的图象上有不重合的两点、,点的纵坐标为2.
(1)求点的横坐标;
(2)过点向轴作垂线,垂足是,试求.
24.如图, OABC 的边 OA 在x 轴的正半轴上,∠AOC=60°,OC=12,∠OCB的平分线交OA 于点D,过点D作DE⊥CD,交 AB 于点E,反比例函数 的图象经过点C与点E.
(1)求k 的值及点D 的坐标.
(2)求证:AD=AE.
(3)求点 E的坐标.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】A
12.【答案】D
13.【答案】5
14.【答案】k>5
15.【答案】
16.【答案】6
17.【答案】或
18.【答案】(1)解:将代入得,,,
将代入得,;
(2)或;
(3)设平移后的直线的表达式为,代入得,,,
故直线向上平移了个单位得到直线,
解方程.,得,,又点在第一象限,
19.【答案】(1)解:将点B(-3,-1)代入y=2x+b,得2×(-3)+b=-1,
∴b=5,
∴一次函数的解析式为y=2x+5;
将点B(-3,-1)代入,
得m=3,
∴反比例函数的解析式为:;
(2)解:解方程组,
得或,
∴点A,
∴不等式的解集为:或;
(3)解:在y=2x+5中,令x=0,则y=5,
∴点C(0,5),
∴OC=5,
∴S△AOB=S△AOC+S△BOC=.
20.【答案】(1)解:当时,设双曲线的解析式为,∵过双曲线,∴的坐标代入,可得,解得:,
∴函数表达式为:
(2)解:设线段AB解析式为,
∵线段AB过点,,代入得,解得:,
∴AB解析式为:,因为大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,当时,代入,可得:,解得:,当,代入,可得:,经检验:是原方程的解,且符合题意,∵,∴这种蔬菜一天内最适合生长的时间为
(3)解:当时,可得:,解得:,经检验:是原方程的解,且符合题意,
∴,
∴恒温系统最多可以关闭10h,才能使蔬菜避免受到伤害.
21.【答案】解:由题意,得vt=240×100,
故t=
22.【答案】(1)解:,.
(2)解:.
23.【答案】(1)解:∵反比例函数的图象上的点纵坐标为2,
∴,
∴,
∴点的横坐标为4;
(2)解:设则有,
,,
∴.
24.【答案】(1)解:如图,过点C作CF⊥x轴,
∵∠AOC=60°,OC=12 ,
∴∠OCF=30°,
∴OF=OC=6,CF=OF=6,
∴C(6,6),
把点C(6,6)代入y=中,得k=6×6=36,
在 OABC中,BC∥OA,
∴∠BCD=∠ODC,
∵CD平分 ∠OCB ,
∴∠BCD=∠OCD,
∴∠ODC=∠OCD,
∴OD=OC=12,
∴D(12,0).
(2)证明:∵OD=OC,∠AOC=60°,
∴△OCD是等边三角形,
∴∠CDO=60°,
∵ DE⊥CD,
∴∠EDA=30°
∵AB∥OC,
∴∠BAx=∠AOC=60°,
∴∠AED=60°-30°=30°
∴∠AED=∠ADE,
∴AE=AD.
(3)解:设AD=AE=a,则E(12+a,a),
把点E坐标代入y=中,得(12+a)·a=36,
解得:a=4或-12(舍),
∴E(18,2 ).
一、单选题
1.已知点A(1,-3)关于x轴的对称点A'在反比例函数 的图像上,则实数k的值为( )
A.3 B. C.-3 D.
2.若反比例函数 的图象经过点(3,﹣2),则k的值为( )
A.﹣9 B.3 C.﹣6 D.9
3.反比例函数y= (x<0)的图象如图所示,随着x值的增大,y值( )
A.增大 B.减小
C.不变 D.先增大后减小
4.若点A(-2,y1),B(-1,y2)都在反比例函数y=的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
5.反比例函数y=与正比例函数y=2x一个交点为(1,2),则另一个交点是( )
A.(-1,-2) B.(-2,-1) C.(1,2) D.(2,1)
6.若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y= 的图象上,则y1,y2,y3的大小关系是( )
A.y3
A. B.
C. D.
8.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
9.如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( )
A.7个 B.8个 C.9个 D.10个
10.如图,为第一象限内一点,过作轴,轴,分别交函数于,两点,若,则为( )
A.12 B.14 C.16 D.18
11.如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B(,),则k的值为( )
A.-6 B.-6 C.-12 D.-12
12.如图,在平面直角坐标系中,线段的端点点A、点D分别在y轴与x轴上.且与反比例函数交于点B、点C,且,面积为3,则k的值为( )
A. B. C. D.
二、填空题
13.如图,在直角坐标系中,点A、B是反比例函数y=
图象上的两点,过A作AM⊥x轴,过B作BN⊥y轴,则图中阴影部分的面积为
14.若反比例函数y=的图象分布在第二、四象限,则k的取值范围是 .
15.如图,已知函数 与 的图象交于A(-4,1)、B(2,-2) 、C(1,-4)三点,根据图象可求得关于x的不等式 的解集为 .
16.如图,在平面直角坐标系中,O为坐标一原点,A是函数 图象上的点,过点A作 轴的平行线交函数 的图象于点B(点B在点A的右边),交 轴于点C,若 则 的值为 .
17.如图,一次函数的图象与反比例函数的图象相交于点和点,则关于的不等式的解集是 .
三、解答题
18.如图,已知正比例函数和反比例函数的图象交于点.
(1)求反比例函数的表达式;
(2)观察图象,直接写出当时,自变量的取值范围;
(3)将直线沿轴向上平移,使平移后的直线与轴交于,与双曲线在第一象限内交于点,求点的坐标.
19.如图,已知一次函数y=2x+b的图象与反比例函数的图象相交于A,B两点,与y轴相交于点C,且点B的坐标为(-3,-1).
(1)求一次函数和反比例函数的表达式及点A的坐标.
(2)若请直接写出x的取值范围.
(3)求△AOB的面积.
20.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)求y与的函数表达式;
(2)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多长时间,才能使蔬菜避免受到伤害?
21.小明要把一篇社会调查报告录入电脑,当他以100字/分钟的速度录入文字时,经过240分钟能完成录入。设他录入文字的速度为v字/分钟时,完成录入的时间为t分钟。求t与v之间的函数关系式(不必写出自变量的取值范围)。
22.如图,一次函数的图象与反比例函数的图象交于、两点,其中点坐标为,点到轴的距离为1.
(1)试确定、的估;
(2)求点的坐标.
23.在反比例函数的图象上有不重合的两点、,点的纵坐标为2.
(1)求点的横坐标;
(2)过点向轴作垂线,垂足是,试求.
24.如图, OABC 的边 OA 在x 轴的正半轴上,∠AOC=60°,OC=12,∠OCB的平分线交OA 于点D,过点D作DE⊥CD,交 AB 于点E,反比例函数 的图象经过点C与点E.
(1)求k 的值及点D 的坐标.
(2)求证:AD=AE.
(3)求点 E的坐标.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】A
12.【答案】D
13.【答案】5
14.【答案】k>5
15.【答案】
16.【答案】6
17.【答案】或
18.【答案】(1)解:将代入得,,,
将代入得,;
(2)或;
(3)设平移后的直线的表达式为,代入得,,,
故直线向上平移了个单位得到直线,
解方程.,得,,又点在第一象限,
19.【答案】(1)解:将点B(-3,-1)代入y=2x+b,得2×(-3)+b=-1,
∴b=5,
∴一次函数的解析式为y=2x+5;
将点B(-3,-1)代入,
得m=3,
∴反比例函数的解析式为:;
(2)解:解方程组,
得或,
∴点A,
∴不等式的解集为:或;
(3)解:在y=2x+5中,令x=0,则y=5,
∴点C(0,5),
∴OC=5,
∴S△AOB=S△AOC+S△BOC=.
20.【答案】(1)解:当时,设双曲线的解析式为,∵过双曲线,∴的坐标代入,可得,解得:,
∴函数表达式为:
(2)解:设线段AB解析式为,
∵线段AB过点,,代入得,解得:,
∴AB解析式为:,因为大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,当时,代入,可得:,解得:,当,代入,可得:,经检验:是原方程的解,且符合题意,∵,∴这种蔬菜一天内最适合生长的时间为
(3)解:当时,可得:,解得:,经检验:是原方程的解,且符合题意,
∴,
∴恒温系统最多可以关闭10h,才能使蔬菜避免受到伤害.
21.【答案】解:由题意,得vt=240×100,
故t=
22.【答案】(1)解:,.
(2)解:.
23.【答案】(1)解:∵反比例函数的图象上的点纵坐标为2,
∴,
∴,
∴点的横坐标为4;
(2)解:设则有,
,,
∴.
24.【答案】(1)解:如图,过点C作CF⊥x轴,
∵∠AOC=60°,OC=12 ,
∴∠OCF=30°,
∴OF=OC=6,CF=OF=6,
∴C(6,6),
把点C(6,6)代入y=中,得k=6×6=36,
在 OABC中,BC∥OA,
∴∠BCD=∠ODC,
∵CD平分 ∠OCB ,
∴∠BCD=∠OCD,
∴∠ODC=∠OCD,
∴OD=OC=12,
∴D(12,0).
(2)证明:∵OD=OC,∠AOC=60°,
∴△OCD是等边三角形,
∴∠CDO=60°,
∵ DE⊥CD,
∴∠EDA=30°
∵AB∥OC,
∴∠BAx=∠AOC=60°,
∴∠AED=60°-30°=30°
∴∠AED=∠ADE,
∴AE=AD.
(3)解:设AD=AE=a,则E(12+a,a),
把点E坐标代入y=中,得(12+a)·a=36,
解得:a=4或-12(舍),
∴E(18,2 ).
