初二数学第二章《实数》总复习

课件53张PPT。实 数一、复习回顾1、无理数的定义：无限不循环小数叫做无理数2、有理数的定义：有限和无限循环小数叫做有理数或整数与分数统称为有理数0.3737737773……4、把下列各数分别填入相应
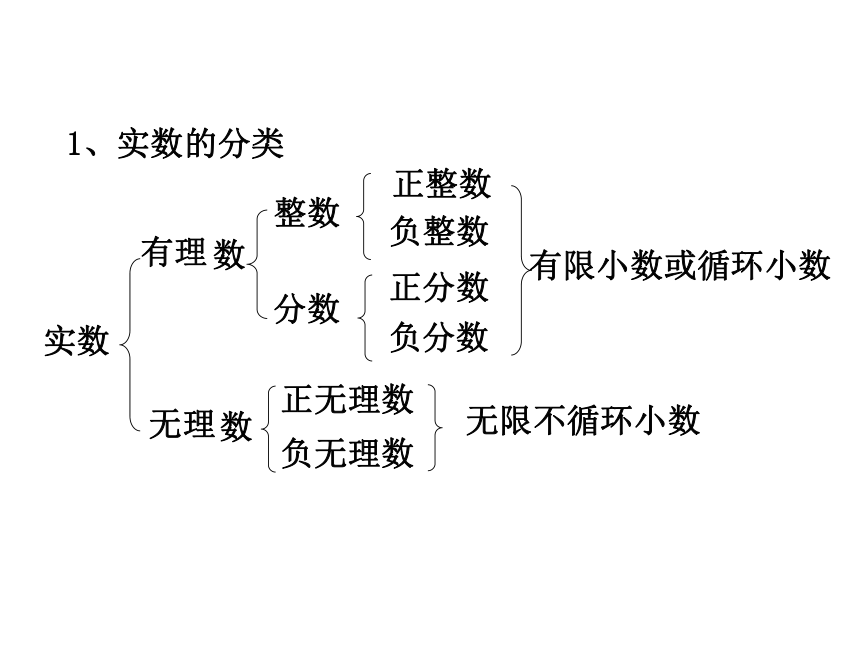
的集合内：有理数集合无理数集合0.3737737773……0二、实数1、实数的定义：有理数和无理数统称为实数即：实数有理数无理数或：实数正实数负实数零1、实数的分类实数 数 数整数分数正整数负整数负分数正分数正无理数负无理数有限小数或循环小数无限不循环小数有理无理2、判断下列说法是否正确：（1）无限小数都是无理数；（2）无理数都是无限小数；（3）带根号的数都是无理数；（4）实数都是无理数；（5）无理数都是实数;（6）没有根号的数都是有理数.3、实数的性质： 在实数范围内，相反数、倒数、
绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。例如：4、求下列各数的相反数、倒数和绝对值：22-77三、想一想 是一个实数，它的相反数为 ;
绝对值为 .如果 那么它的
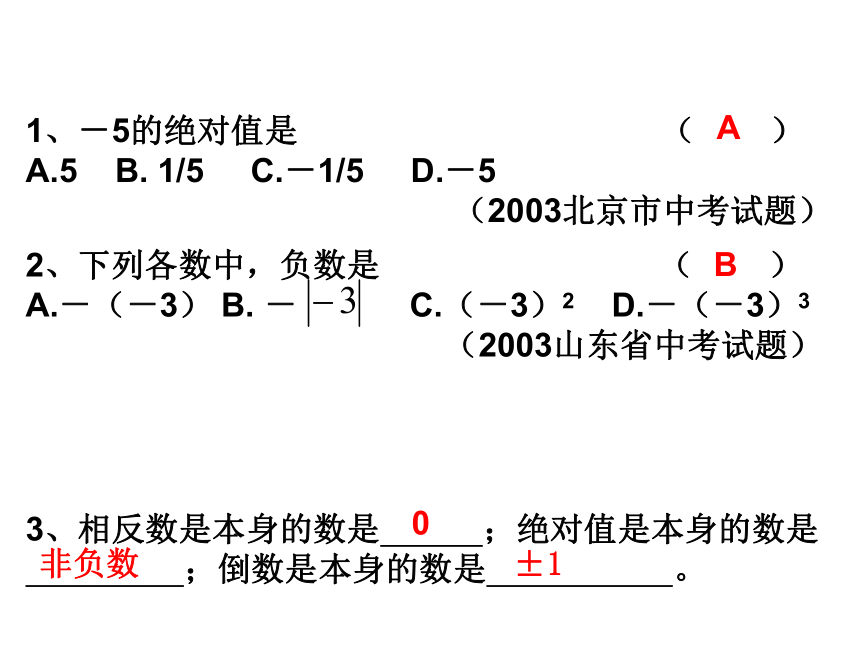
倒数为 .1、－5的绝对值是 （ ）
A.5 B. 1/5 C.－1/5 D.－5
（2003北京市中考试题）2、下列各数中，负数是 （ ）
A.－（－3） B. － C.（－3）2 D.－（－3）3
（2003山东省中考试题） 3、相反数是本身的数是 ；绝对值是本身的数是
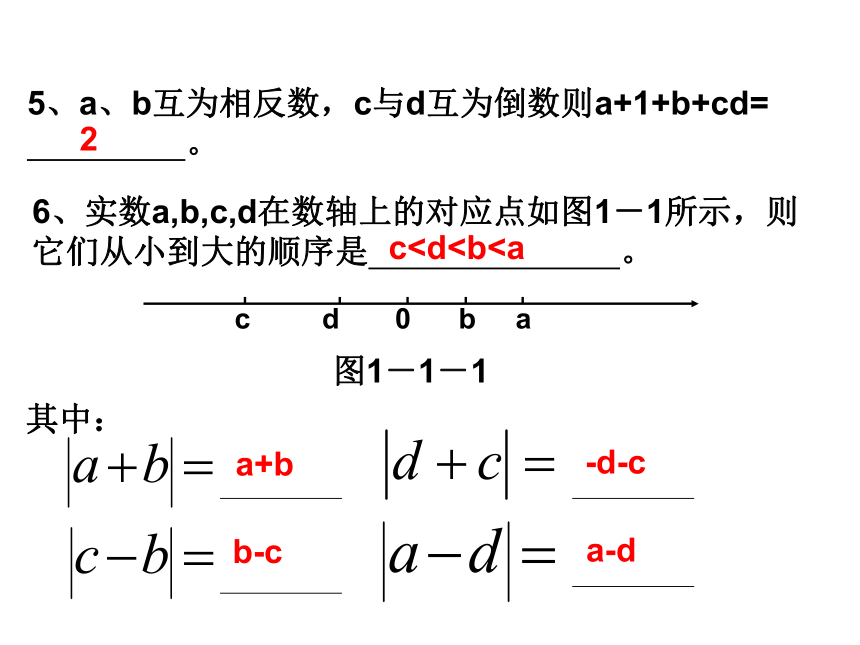
；倒数是本身的数是 。AB0非负数±15、a、b互为相反数，c与d互为倒数则a+1+b+cd=
。6、实数a,b,c,d在数轴上的对应点如图1－1所示，则
它们从小到大的顺序是 。其中：2c （2） －2的绝对值是 ；
（3）若 ，且xy>0，x+y= 。 例2、把下列各数填到相应的集合里:整数集合：{ }； 分数集合：{ }； 有理数集合： ； 无理数集合：{ }。 1/32-;tan45°-3 3-1；3.14；227;sin30°；｜-3.2｜；-0.32·1· 3-1；3-27；3.14；227；sin30°；tan45°-3;-0.32·1·;｜-3.2｜ ;-π；0.100110001… 3或-3四、议一议0-1121AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗?在数轴上作出 的对应点.0123-112012-1-2A一个实数a 每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的. 同样,在数轴上,右边的点表示的数比左边的点表示的数大.数轴上一个点有一个实数有一个实数数轴上一个点一、填空题：1、 4的平方根是 ；±22、-125的立方根是 ；-53、化简：７、下列说法正确的是：（1）无限小数是无理数（2）有理数都是有限小数（3）一个数的立方根不一定是
无理数（4）任何实数都有唯一的立方根（5）只有正实数才有算术平方根（7）不带根号的数都是有理数（6）任何数的平方根有两
个，它们互为相反数（8）两个无理数的和一定是
无理数（9）两个无理数的积一定是
无理数（10）若正数a的一个平方根
是b，那么a的另一个平方
根是-b.（11）正数的两个平方根的和为0（12）没有平方根的数也没有立方根若a为有理数,b为无理数,
则 ab必为无理数8、π的整数部分为3，则它
的小数部分是 ；π-3210、比较大小：二、选择题：1、(-3)2的算术平方根是（ ）（A）无意义（B）±3（C）-3（D） 34、下列运算正确的是（ ）一．选择题:无理数的个数是（ ） (A) 2 ( B) 3 (C) 4 (D) 5C1、在下列各数2、一个长方形的长与宽分别
时6、3，它的对角线的长可
能是（ ） 整数(D) 无理数 (C) 有理数(B) 分数D3、下列六种说法正确的个数是 (1)、无限小数都是无理数 (2)、正数、零和负数统称有理数 (3)、无理数的相反数还是无理数 (4)、无理数与无理数的和一定还
是无理数 (5)、无理数与有理数的和一定是
无理数 (6)、 无理数与有理数的积一定仍是
无理数 4、下列语句中正确的是（ ） (A) -9的平方根是-3 (B) 9的平方根是3 （D） 9的算术平方根是3 D5、下列运算中，正确的是（ ） A6、的平方根是（ ） (A) (C) 5 (B) (D) 7、下列运算正确的是( ) DDC二. 填空题： 1、9的算术平方根是 ; 2、(-5)0的立方根是 ; 3、10-2的平方根是 ; 31±0.10251、－5的绝对值是 （ ）
A.5 B. C. － D.－5
（2003北京市中考试题）2、下列各数中，负数是 （ ）
A.－（－3） B. － C.（－3）2 D.－（－3）3
（2003山东省中考试题） 3、相反数是本身的数是 ；绝对值是本身的数是
；倒数是本身的数是 。AB0非负数±15、a、b互为相反数，c与d互为倒数则a+1+b+cd=
。6、实数a,b,c,d在数轴上的对应点如图1－1所示，则
它们从小到大的顺序是 。其中：2c （2） －2的绝对值是 ；
（3）若 ，且xy>0，x+y= 。 例2、把下列各数填到相应的集合里:整数集合：{ }； 分数集合：{ }； 有理数集合： ； 无理数集合：{ }。 ;tan45°-3 3-1；3.14；227;sin30°；｜-3.2｜；-0.32·1· 3-1；3-27；3.14；227；sin30°；tan45°-3;-0.32·1·;｜-3.2｜ ;-π；0.100110001… 3或-3例3、比较大小： 与例4、已知实数a、b在数轴上对应点的位置如图1－2；
化简：解：∵(-2+ )-(-2+ )=-2+ +2- = - ＞0
∴-2+ ＞-2+
另解：直接由正负决定-2+ ＞-2+
解：由图知：b＜a＜0，∴a-b＞0，a+b＜0.
∴｜a-b｜+ =(a-b)+｜a+b｜
=a-b+［-(a+b)］
=a-b-a-b
=-2b.b a ox解：∵｜3a+4｜≥0且(4b-3)2≥0
而｜3a+4｜+(4b-3)2=0
∴｜3a+4｜=0且(4b-3)２＝０
∴a=-43，b=34
∴a2003b2004=(-4/3)2003·(3/4)2004=-34
有理数集合：{ }； 1、把下列各数填在相应的大括号内：整数集合：{ ……}； 奇数集合：{ ……}； 无理数集合：{ }。 -1，0， -1-1，，3.14，0，3.3·3·，cos60°， π,-,tan30°,2.1010010001… 2、下列说法中，错误的个数是 （ ）①无理数都是无限小数；②无理数都是开方开不尽的数；
③带根号的都是无理数；④无限小数都是无理数。 A.1个； B.2个； C.3个； D.4个。3、数轴上的点与（ ）一一对应。 A.整数； B.有理数； C.无理数； D.实数。4、下列各组数中，相等的是 （ ）A.B.C.D.CDD5、下列各组数中，互为相反数是 （ ） B.C. D.（重庆2003年中考题）6、7的绝对值等于 ，－4的倒数等于 。（南通2003年中考题）C7-1/4要点、考点聚焦1.几个重要的运算律：
(1)加法的交换律：a+b=b+a
(2)加法的结合律：(a+b)+c=a+(b+c)
(3)乘法的交换律：ab=ba
(4)加法的结合律：(ab)c=a(bc)
(5)乘法对加法的分配律：a(b+c)=ab+ac
2.实数的运算主要有：加、减、乘、除、乘方、开
方.实数的运算顺序：先乘方、开方，再乘、除，最
后算加、减，有括号的先算括号里面的.
4.有效数字是指一个数从左边第一个不为零的数字起
到右边所有的数字.3.科学记数法的一般形式为：a×10n(1≤a≤10，n
为整数).课前热身1、(2003年·黄冈市)2003年6月1日9时，举世瞩目的三
峡工程正式下闸蓄水，首批4台组率先发电，预计年内可
发电55 000 000 000度，这个数用科学记数法表示，记
为 .
2、将2000800保留四个有效数字是 ，用四
舍五入法，把它精确到十万位的近似数用科学记数法表
示为 .
3、(2002年·厦门)计算：3-1+(2-1)0= 。5.5×10102.0×1062.001×10６4/34、(2002年·江苏淮安)计算：-32÷(-3)２+3 -1×(-6)= . -35、人类的DNA是很长的链，最短的22号染色体也长达
30 000 000个核苷酸，30 000 000用科学记数法表示为
( )
A.3×10８ B.3×107
C.3×106 D.0.3×108
6、(2003年·四川省)我国的国土面积约为9596960平方
千米，按四舍五入法保留两个有效数字，并用科学记数
法表示为( )
A.96×105平方千米 B.9.60×10６平方千米
C.9.6×106平方千米 D.0.96×107平方千米
BC7、计算：0.25×(-1/2)-2+( -1)０=( )
A.2 B.54 C.0 D. 17/16
8、((2003年·长沙市)为期一周的中国·湖南第四届(国
际)农博会于2002年12月在长沙举行，本届农博会成
交总额达到611 000万元，用科学记数法表示为
万元 A6.11×10５典型例题解析例1、 (2002年·上海)在张江高科技园区的上海超级计算机中心内，被称为“神威Ⅰ”的计算机的运算速度为每秒384 000 000 000次，这个速度用科学记数法表示为每秒 次. 解：
384000 000 000=3.84×1011.解：原式=［-9×2+3×(-8)+24］÷［-9］
=(-18-24+24)÷(-9)
=2
例3、
计算：［-32×2+3×(-2)3-4×(-6)］÷［- ］. 例4、
(2002年·北京海淀区)x、y是实数， +y2-6y+9=0，
若axy-3x=y,则实数a的值是( )
A.1/4 B.-1/4
C.7/4 D.-7/4A【例】 (2002年·山东济南市)2001年中国银行外汇交易创历史新高，累计成交750.33亿美元，若1美元可兑换8.2779元人民币，用科学记数法表示2001年交额相当于人民币 亿元(精确到亿位)( )
A.6.211×10３ B.6.211×1011
C.6.21×10３ D.6.21×1011解：
∵750.33×8.2779=6211(亿元)
∴6211=6.211×10３
∴本题选择Ａ.
A1、(2003年·吉林省)今年6月1日，举世瞩目的三峡工
程正式下闸蓄水，26台机组年发电量将达到84 700
000 000千瓦时，用科学记数法应表示为( )
A.8.47×1010千瓦时 B.8.47×108千瓦时
C.8.47×109千瓦时 D.8.47×1011千瓦时2、计算(2-1)２的结果等于( )
A.2 B.4 C.14 D.3、一天有8.64×104秒，一年若按365天计算，则一年
有多少秒，可用科学记数法表示为( )
A.3.1536×10 7 B.3.1536×106
C.3.1536×103 D.3.1536×104
CAA4、某服装商贩同时卖出两套服装，每套均卖168元，
以成本计算，其中一套盈利20%，另一套亏本20%，
则这两次出售中商贩( )
A.不赚不赔 B.赚37.2元
C.赚14元 D.赔14元5、下列各数(-2)０、-(-2)、(-2)2、(-2)3中，负数的个
数为( )个
A.1 B.2 C.3 D.4AD