19.2平行四边形(1)
图片预览




文档简介
(共21张PPT)
19.2平行四边形(1)
教学目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角
相等的性质;
3.初步体会几何研究的一般思路与方法.
教学重点:
平行四边形边角性质的证明和应用.
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
复习引入
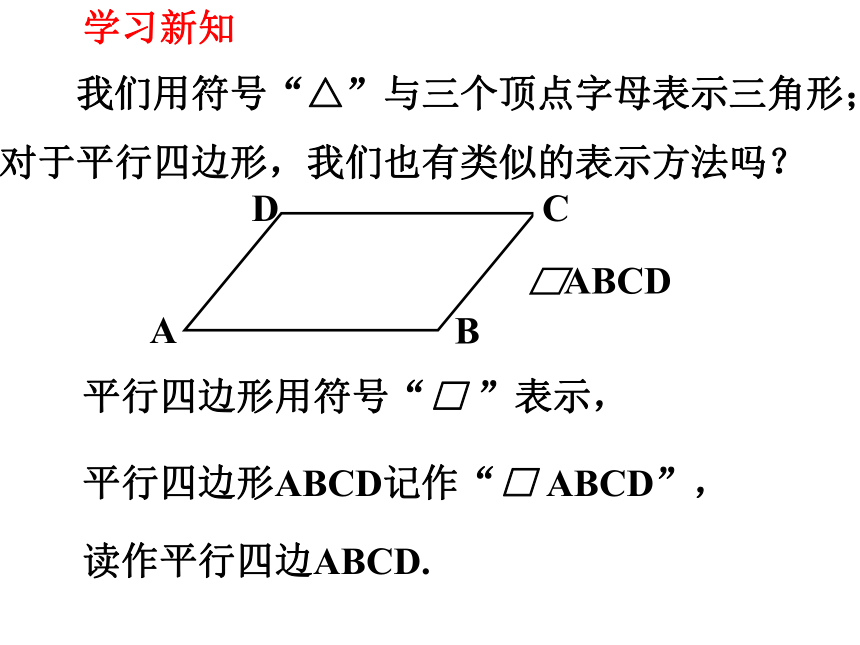
平行四边形ABCD记作“□ ABCD”,
读作平行四边ABCD.
我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,我们也有类似的表示方法吗?
ABCD
平行四边形用符号“□ ”表示,
学习新知
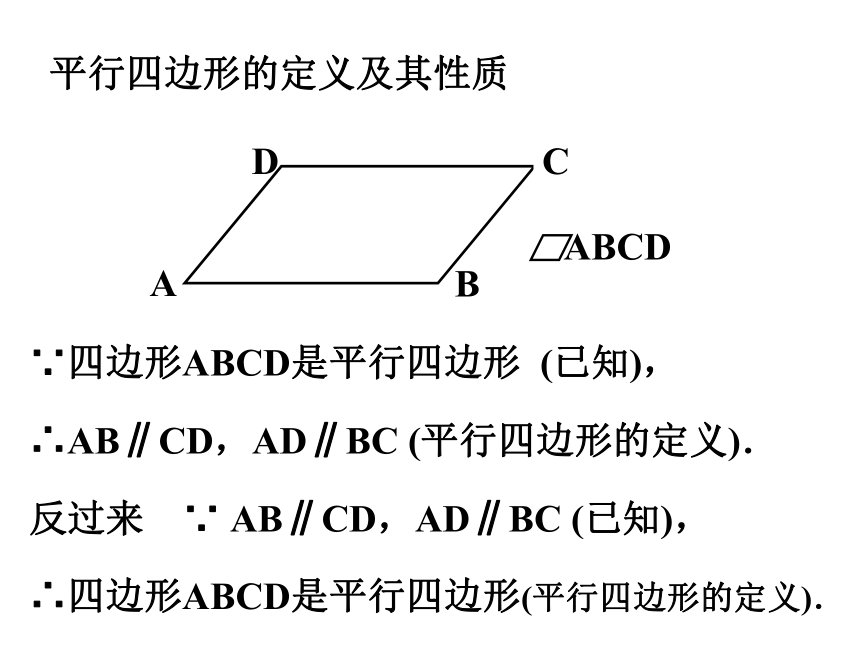
∵四边形ABCD是平行四边形 (已知),
∴AB∥CD,AD∥BC (平行四边形的定义).
反过来 ∵ AB∥CD,AD∥BC (已知),
∴四边形ABCD是平行四边形(平行四边形的定义).
平行四边形的定义及其性质
ABCD
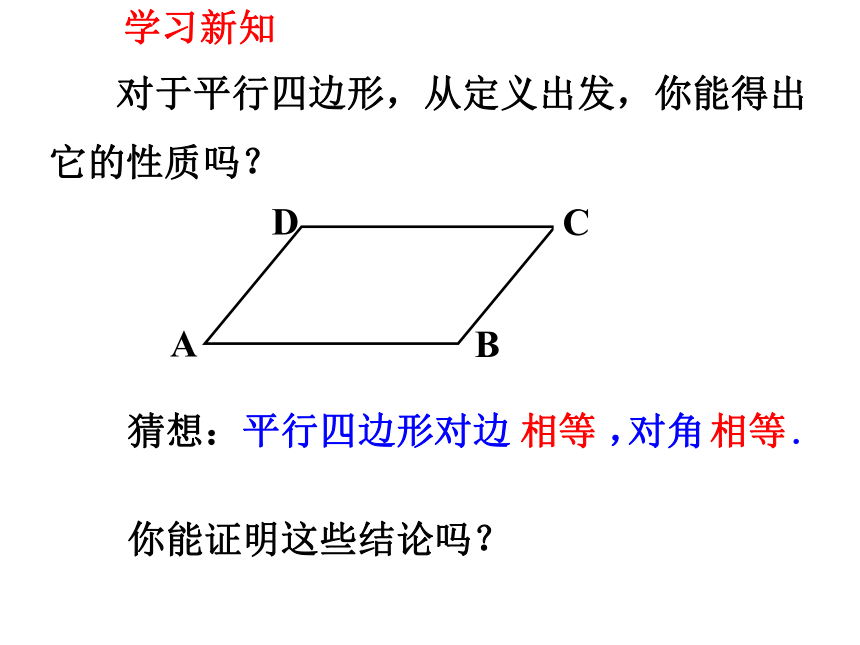
对于平行四边形,从定义出发,你能得出
它的性质吗?
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是什么?
导入新知
对于平行四边形,从定义出发,你能得出它的性质吗?
你能证明这些结论吗?
猜想:平行四边形对边 ,
对角 .
相等
相等
学习新知
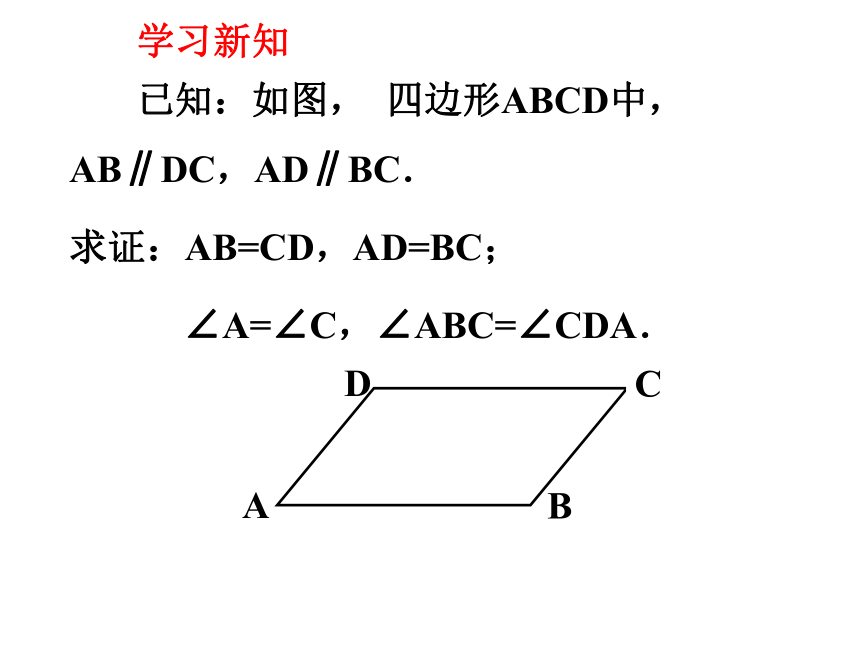
已知:如图, 四边形ABCD中,AB∥DC,AD∥BC.
求证:AB=CD,AD=BC;
∠A=∠C,∠ABC=∠CDA.
学习新知
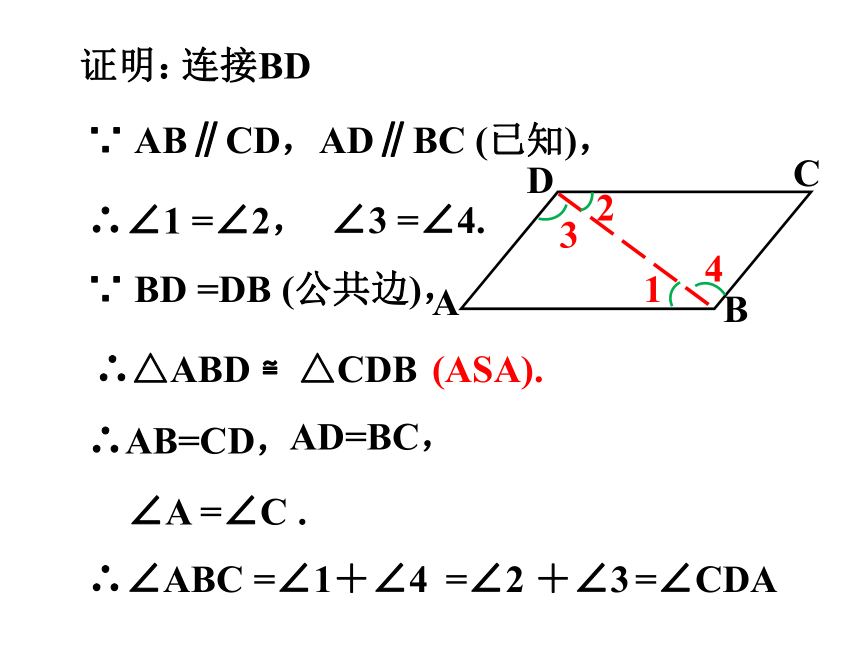
证明:
连接BD
∵ AB∥CD,AD∥BC (已知),
1
2
3
4
∴∠1 =∠2,
∠3 =∠4.
∵ BD =DB (公共边),
∴△ABD ≌△CDB
∴AB=CD,
AD=BC,
∠A =∠C .
(ASA).
∴∠ABC =∠1+∠4
=∠2 +∠3
=∠CDA
平行四边形的性质定理:
平行四边形的对边相等,
平行四边形的对角相等.
∵四边形ABCD是平行四边形(已知),
∴AB=CD, AD=BC (平行四边形的性质);
∠A=∠C,∠B=∠D (平行四边形的性质).
形成新知
符号语言:
例1 已知:如图, □ABCD中,BE平分∠ABC交AD于点E.
B
C
D
A
E
(1)如果AE =2,求CD的长;
(2)如果∠AEB=40°,求∠C的度数.
例题解析
例1 已知:如图, □ABCD中,BE平分∠ABC交AD于点E.
B
C
D
A
E
(1)如果AE =2,求CD的长;
要求CD的长
要求AB的长
要求∠1=∠2
要求∠2=∠3
AD∥BC
四边形ABCD是平行四边形
1
2
3
要求AB=AE
分析:
例1 已知:如图, □ABCD中,BE平分∠ABC交AD于点E.
(1)如果AE =2,求CD的长;
∴CD=2.
AB=CD.
∴∠1=∠2,
∴∠2=∠3.
∴AD∥BC,
∵四边形ABCD是平行四边形,
B
C
D
A
E
1
2
3
∴AB=AE.
∵AE=2,
∴CD=AE.
∵BE平分∠ABC,
∴∠1=∠3,
解:(1)
例1 已知:如图, □ABCD中,BE平∠ABC交AD于点E.
∵∠AEB=40°,
(2)如果∠AEB=40°,求∠C的度数.
∠1=∠AEB,
∴∠A=180°-(∠1+∠AEB)
=180°-(40°+40°)
=100°.
∵∠C=∠A,
∴∠C=100°.
(2)
B
C
D
A
E
1
A
B
C
D
解:
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠ D.
∵∠A=60°,
∴∠C=60°,
∴∠B=∠D
=(360°-60°×2)÷2=120°.
1.在□ABCD中,已知∠A=60°,
求∠B,∠C,∠D的度数.
练习巩固
A
B
C
D
解:
∵四边形ABCD是平行四边形,
∴AB=CD=a,BC=AD=b.
∴这个平行四边形的周长为
2.在□ABCD中,已知AB=a,BC=b,
求这个平行四边形的周长.
AB+BC+CD+AD
=2(a+b).
=a+b+a+b
(1)本节课我们学习了哪些知识?
(2)通过本节的学习和过去三角形的学习经历,你
认为对一个几何图形的研究通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?
你认为有必要进一步研究思考吗?
课堂小结
1.在□ABCD中,AB=6,BC=8,则□ABCD的周长是( ).
A.28 B.16 C.14 D.12
2.在□ABCD中, ∠B+∠D=210°, 则∠A的度数是( ).
练习巩固
A. 55° B. 65° C.75° D. 85°
A
C
3.如图,□ABCD 中, ∠ADC= 119°,
BE⊥DC于点E, DF⊥BC于点F,BE于DF交于点H,则∠BHF= 度.
A
B
D
C
E
F
H
61
4.如图,□ABCD 中, AB=5,BC=7,
∠BAD和∠ADC的平分线,分别交BC于E,F两,则EF的长度为 .
A
B
D
C
E
F
3
今天作业
课本P84页第1、2题
19.2平行四边形(1)
教学目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角
相等的性质;
3.初步体会几何研究的一般思路与方法.
教学重点:
平行四边形边角性质的证明和应用.
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
复习引入
平行四边形ABCD记作“□ ABCD”,
读作平行四边ABCD.
我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,我们也有类似的表示方法吗?
ABCD
平行四边形用符号“□ ”表示,
学习新知
∵四边形ABCD是平行四边形 (已知),
∴AB∥CD,AD∥BC (平行四边形的定义).
反过来 ∵ AB∥CD,AD∥BC (已知),
∴四边形ABCD是平行四边形(平行四边形的定义).
平行四边形的定义及其性质
ABCD
对于平行四边形,从定义出发,你能得出
它的性质吗?
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是什么?
导入新知
对于平行四边形,从定义出发,你能得出它的性质吗?
你能证明这些结论吗?
猜想:平行四边形对边 ,
对角 .
相等
相等
学习新知
已知:如图, 四边形ABCD中,AB∥DC,AD∥BC.
求证:AB=CD,AD=BC;
∠A=∠C,∠ABC=∠CDA.
学习新知
证明:
连接BD
∵ AB∥CD,AD∥BC (已知),
1
2
3
4
∴∠1 =∠2,
∠3 =∠4.
∵ BD =DB (公共边),
∴△ABD ≌△CDB
∴AB=CD,
AD=BC,
∠A =∠C .
(ASA).
∴∠ABC =∠1+∠4
=∠2 +∠3
=∠CDA
平行四边形的性质定理:
平行四边形的对边相等,
平行四边形的对角相等.
∵四边形ABCD是平行四边形(已知),
∴AB=CD, AD=BC (平行四边形的性质);
∠A=∠C,∠B=∠D (平行四边形的性质).
形成新知
符号语言:
例1 已知:如图, □ABCD中,BE平分∠ABC交AD于点E.
B
C
D
A
E
(1)如果AE =2,求CD的长;
(2)如果∠AEB=40°,求∠C的度数.
例题解析
例1 已知:如图, □ABCD中,BE平分∠ABC交AD于点E.
B
C
D
A
E
(1)如果AE =2,求CD的长;
要求CD的长
要求AB的长
要求∠1=∠2
要求∠2=∠3
AD∥BC
四边形ABCD是平行四边形
1
2
3
要求AB=AE
分析:
例1 已知:如图, □ABCD中,BE平分∠ABC交AD于点E.
(1)如果AE =2,求CD的长;
∴CD=2.
AB=CD.
∴∠1=∠2,
∴∠2=∠3.
∴AD∥BC,
∵四边形ABCD是平行四边形,
B
C
D
A
E
1
2
3
∴AB=AE.
∵AE=2,
∴CD=AE.
∵BE平分∠ABC,
∴∠1=∠3,
解:(1)
例1 已知:如图, □ABCD中,BE平∠ABC交AD于点E.
∵∠AEB=40°,
(2)如果∠AEB=40°,求∠C的度数.
∠1=∠AEB,
∴∠A=180°-(∠1+∠AEB)
=180°-(40°+40°)
=100°.
∵∠C=∠A,
∴∠C=100°.
(2)
B
C
D
A
E
1
A
B
C
D
解:
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠ D.
∵∠A=60°,
∴∠C=60°,
∴∠B=∠D
=(360°-60°×2)÷2=120°.
1.在□ABCD中,已知∠A=60°,
求∠B,∠C,∠D的度数.
练习巩固
A
B
C
D
解:
∵四边形ABCD是平行四边形,
∴AB=CD=a,BC=AD=b.
∴这个平行四边形的周长为
2.在□ABCD中,已知AB=a,BC=b,
求这个平行四边形的周长.
AB+BC+CD+AD
=2(a+b).
=a+b+a+b
(1)本节课我们学习了哪些知识?
(2)通过本节的学习和过去三角形的学习经历,你
认为对一个几何图形的研究通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?
你认为有必要进一步研究思考吗?
课堂小结
1.在□ABCD中,AB=6,BC=8,则□ABCD的周长是( ).
A.28 B.16 C.14 D.12
2.在□ABCD中, ∠B+∠D=210°, 则∠A的度数是( ).
练习巩固
A. 55° B. 65° C.75° D. 85°
A
C
3.如图,□ABCD 中, ∠ADC= 119°,
BE⊥DC于点E, DF⊥BC于点F,BE于DF交于点H,则∠BHF= 度.
A
B
D
C
E
F
H
61
4.如图,□ABCD 中, AB=5,BC=7,
∠BAD和∠ADC的平分线,分别交BC于E,F两,则EF的长度为 .
A
B
D
C
E
F
3
今天作业
课本P84页第1、2题
