19.2平行四边形(2)
图片预览








文档简介
(共24张PPT)
19.2平行四边形(2)
教学目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角
相等的性质;
3.初步体会几何研究的一般思路与方法.
教学重点:
平行四边形边角性质的证明和应用.
平行四边形的对边相等
平行四边形的对角相等
什么是平行四边形,平行四边形有哪些性质?
两组对边分别平行的四边形叫做平行四边形.
平行四边形的对边平行
复习旧知
1.已知四边形ABCD是平行四边形,则下列结论不一定成立的是是( ).
A. ∠A+∠C=180° B. ∠B=∠D
C.AD∥BC D.AB=CD
2.在□ABCD中, ∠B比∠C大20°, 则∠A的度数是 .
复习巩固
80°
A
结论:夹在两条平行线间的平行线段相等.
问题1:如图,直线 l1∥ l2 ,AB、CD是夹在l1 、 l2之间的两条平行线段,AB与CD相等?你能得到什么结论?
∵ l1∥l2 ,AB∥CD,
∴AB=CD.
A
B
C
D
l1
l2
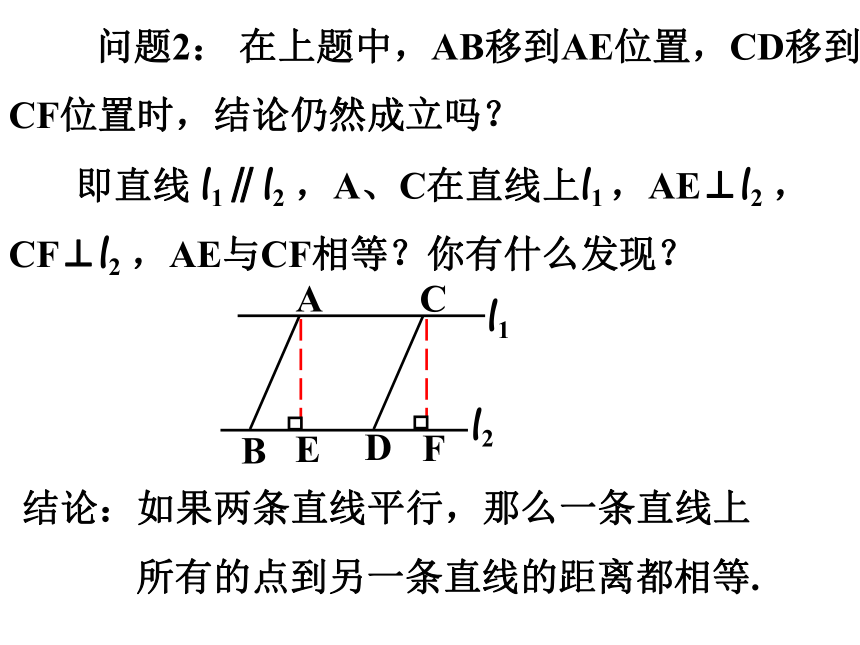
问题2: 在上题中,AB移到AE位置,CD移到CF位置时,结论仍然成立吗?
即直线 l1∥l2 ,A、C在直线上l1 ,AE⊥l2 , CF⊥l2 ,AE与CF相等?你有什么发现?
结论:如果两条直线平行,那么一条直线上
所有的点到另一条直线的距离都相等.
A
B
C
D
l1
l2
E
F
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
两条平行线中,一条直线上任意一点到另一条直线上的距离叫这两条平行线之间的距离,如图中的线段AE是直线l1和直线l2之间的距离.
推论2 :平行线间的距离处处相等.
∵ l1∥l2,AE⊥l2,CF⊥l2,
∴ AE=CF.
A
B
C
D
l1
l2
E
F
1.这是楼梯扶手,它是用不锈钢管制作的,这些竖直的钢管长度相等吗 ?
2.在笔直的铁轨上,夹在两根铁轨
之间的枕木是否一样长呢?
例2 已知:如图, □ABCD中,AB = 4,AD = 5,∠B = 45°.求直线AD与直线BC之间的距离,
直线AB和直线DC之间的距离.
A
B
C
D
45°
5
4
E
分析:
怎样表示直线AD与直线BC之间的距离?
怎样表示直线AB与直线DC之间的距离?
F
例题解析
解 : 过点A作AE⊥BC 于E,AF⊥CD于F,
∴ 线段AE,AF的长分别为点A到
直线BC和直线CD的距离,
∴ 线段AE的长为直线AD和
直线BC之间的距离,
线段AF的长为直线AB和
直线CD之间的距离.
∵ 在Rt△ABE中,∠AEB = 90°,∠B = 45°,
∴∠BAE=∠B=45°.
∴BE = AE.
F
A
B
C
D
45°
5
4
E
∵ 在Rt△ABE中,∠AEB = 90°,∠B = 45°,
∴∠BAE=∠B=45°.
∴BE = AE.
F
A
B
C
D
45°
5
4
E
∵ AE2 + BE2=AB2,
AB=4,
∴2AE2=42.
∴AE2=8.
∴AE= .
2
2
∴直线AD和直线BC之间的距离为 .
2
2
∵ 在Rt△AFD中,∠AFD = 90°,∠D = 45°,
∴∠DAF=∠D=45°.
∴AF = DF.
F
A
B
C
D
45°
5
4
E
∵ AF2 + DF2=AD2,
AD=5,
∴2AF2=52.
∴AF2= .
∴AF= .
25
2
5
2
2
∴直线AB和直线CD之间的距离为 .
5
2
2
A
B
C
D
1. 如图, □ABCD中,AC⊥AB ,AB=6,BC=10,则
(1)直线AB与直线CD的距离为 ;
(2)直线AD与直线BC的距离为 .
8
4.8
E
复习巩固
2.如图,直线l1∥l2 ,A、B是直线l1 上的两点,C、D是直线 l2上的两点,若A、B、C为定点,点D在直线l2上移动,则无论D点移动到什么位置,总有 与△ABC的面积相等,理由
是 .
△ABD
平行线间距离处处相等
C
A
D
B
l2
l1
A
B
C
C′
A′
B′
例3. 如图,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△A′B′C′.
求证:△ABC的顶点分别是△A′B′C′三边的中点.
AB′=AC′
AB′=BC
AB∥CB′
BC ∥AB′
AC∥BC′
BC ∥AC′
AC′=BC
顶点A是△A′B′C′边的中点.
分析:
A
B
C
C′
A′
B′
3. 如图,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△A′B′C′.
求证:△ABC的顶点分别是△A′B′C′三边的中点.
∴ AB′=AC′.
∴ AB′=BC.
∵ AB∥CB′,BC ∥AB′,
∵ AC∥BC′,BC ∥AC′,
∴ AC′=BC.
同理: BC′=BA′,CA′=CB′.
∴ △ABC的顶点A、B、C
分别是△A′B′C′三边的中点.
证明:
A
B
C
D
E
3. 在□ABCD中,BC=2AB,点E为边BC的中点. 求证:AE⊥ED.
练习巩固
四边形ABCD是平行四边形,
AB=CD
1
A
B
C
D
E
2
5
3
6
4
BC=2BE,
BC=2CE,
AB=BE,
CE=CD.
∠5=∠6,
∠4=∠3.
∠1=∠5,
∠2=∠4.
∠1+∠2=90°
∠AED=90°
AE⊥ED
3. 在□ABCD中,BC=2AB,点E为边BC的中点. 求证:AE⊥ED.
3. 在□ABCD中,BC=2AB,点E为边BC的中点. 求证:AE⊥ED.
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,
AB=CD.
1
A
B
C
D
E
2
5
3
6
4
∴∠2=∠3,
∠1=∠6.
∵ BC=2AB,
∴BC=2CD,
∵点E为边BC的中点,
∴BC=2BE,
BC=2CE,
∴AB=BE,
CE=CD.
∴∠5=∠6,
∠4=∠3.
∴∠1=∠5,
∠2=∠4.
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,
AB=CD.
1
A
B
C
D
E
2
5
3
6
4
∴∠2=∠3,
∠1=∠6.
∵ BC=2AB,
∴BC=2CD,
∵点E为边BC的中点,
∴BC=2BE,
BC=2CE,
∴AB=BE,
CE=CD.
∴∠5=∠6,
∠4=∠3.
∴∠1=∠5,
∠2=∠4.
∵AB∥DC,
∴∠5+∠1+∠2+∠4=180°.
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°.
∴∠AED=90°,
∴AE⊥ED.
(1) 这节课,我们学习了哪些新的认识?
谈谈你的收获.
(2) 你对平行四边形及性质有哪些认识?
课堂小结
1.如图,AD∥BC 中, ∠A =∠D=90°,
AB=1,AD=2, 则直线AD,BC之间的距离为
= .
A
B
D
C
巩固提高
2. 在□ABCD中,AB=4cm,BC=6cm.若□ABCD的高为5cm,则它的面积为 cm2.
1
20
今天作业
课本P84页第4、6题
19.2平行四边形(2)
教学目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角
相等的性质;
3.初步体会几何研究的一般思路与方法.
教学重点:
平行四边形边角性质的证明和应用.
平行四边形的对边相等
平行四边形的对角相等
什么是平行四边形,平行四边形有哪些性质?
两组对边分别平行的四边形叫做平行四边形.
平行四边形的对边平行
复习旧知
1.已知四边形ABCD是平行四边形,则下列结论不一定成立的是是( ).
A. ∠A+∠C=180° B. ∠B=∠D
C.AD∥BC D.AB=CD
2.在□ABCD中, ∠B比∠C大20°, 则∠A的度数是 .
复习巩固
80°
A
结论:夹在两条平行线间的平行线段相等.
问题1:如图,直线 l1∥ l2 ,AB、CD是夹在l1 、 l2之间的两条平行线段,AB与CD相等?你能得到什么结论?
∵ l1∥l2 ,AB∥CD,
∴AB=CD.
A
B
C
D
l1
l2
问题2: 在上题中,AB移到AE位置,CD移到CF位置时,结论仍然成立吗?
即直线 l1∥l2 ,A、C在直线上l1 ,AE⊥l2 , CF⊥l2 ,AE与CF相等?你有什么发现?
结论:如果两条直线平行,那么一条直线上
所有的点到另一条直线的距离都相等.
A
B
C
D
l1
l2
E
F
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
两条平行线中,一条直线上任意一点到另一条直线上的距离叫这两条平行线之间的距离,如图中的线段AE是直线l1和直线l2之间的距离.
推论2 :平行线间的距离处处相等.
∵ l1∥l2,AE⊥l2,CF⊥l2,
∴ AE=CF.
A
B
C
D
l1
l2
E
F
1.这是楼梯扶手,它是用不锈钢管制作的,这些竖直的钢管长度相等吗 ?
2.在笔直的铁轨上,夹在两根铁轨
之间的枕木是否一样长呢?
例2 已知:如图, □ABCD中,AB = 4,AD = 5,∠B = 45°.求直线AD与直线BC之间的距离,
直线AB和直线DC之间的距离.
A
B
C
D
45°
5
4
E
分析:
怎样表示直线AD与直线BC之间的距离?
怎样表示直线AB与直线DC之间的距离?
F
例题解析
解 : 过点A作AE⊥BC 于E,AF⊥CD于F,
∴ 线段AE,AF的长分别为点A到
直线BC和直线CD的距离,
∴ 线段AE的长为直线AD和
直线BC之间的距离,
线段AF的长为直线AB和
直线CD之间的距离.
∵ 在Rt△ABE中,∠AEB = 90°,∠B = 45°,
∴∠BAE=∠B=45°.
∴BE = AE.
F
A
B
C
D
45°
5
4
E
∵ 在Rt△ABE中,∠AEB = 90°,∠B = 45°,
∴∠BAE=∠B=45°.
∴BE = AE.
F
A
B
C
D
45°
5
4
E
∵ AE2 + BE2=AB2,
AB=4,
∴2AE2=42.
∴AE2=8.
∴AE= .
2
2
∴直线AD和直线BC之间的距离为 .
2
2
∵ 在Rt△AFD中,∠AFD = 90°,∠D = 45°,
∴∠DAF=∠D=45°.
∴AF = DF.
F
A
B
C
D
45°
5
4
E
∵ AF2 + DF2=AD2,
AD=5,
∴2AF2=52.
∴AF2= .
∴AF= .
25
2
5
2
2
∴直线AB和直线CD之间的距离为 .
5
2
2
A
B
C
D
1. 如图, □ABCD中,AC⊥AB ,AB=6,BC=10,则
(1)直线AB与直线CD的距离为 ;
(2)直线AD与直线BC的距离为 .
8
4.8
E
复习巩固
2.如图,直线l1∥l2 ,A、B是直线l1 上的两点,C、D是直线 l2上的两点,若A、B、C为定点,点D在直线l2上移动,则无论D点移动到什么位置,总有 与△ABC的面积相等,理由
是 .
△ABD
平行线间距离处处相等
C
A
D
B
l2
l1
A
B
C
C′
A′
B′
例3. 如图,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△A′B′C′.
求证:△ABC的顶点分别是△A′B′C′三边的中点.
AB′=AC′
AB′=BC
AB∥CB′
BC ∥AB′
AC∥BC′
BC ∥AC′
AC′=BC
顶点A是△A′B′C′边的中点.
分析:
A
B
C
C′
A′
B′
3. 如图,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△A′B′C′.
求证:△ABC的顶点分别是△A′B′C′三边的中点.
∴ AB′=AC′.
∴ AB′=BC.
∵ AB∥CB′,BC ∥AB′,
∵ AC∥BC′,BC ∥AC′,
∴ AC′=BC.
同理: BC′=BA′,CA′=CB′.
∴ △ABC的顶点A、B、C
分别是△A′B′C′三边的中点.
证明:
A
B
C
D
E
3. 在□ABCD中,BC=2AB,点E为边BC的中点. 求证:AE⊥ED.
练习巩固
四边形ABCD是平行四边形,
AB=CD
1
A
B
C
D
E
2
5
3
6
4
BC=2BE,
BC=2CE,
AB=BE,
CE=CD.
∠5=∠6,
∠4=∠3.
∠1=∠5,
∠2=∠4.
∠1+∠2=90°
∠AED=90°
AE⊥ED
3. 在□ABCD中,BC=2AB,点E为边BC的中点. 求证:AE⊥ED.
3. 在□ABCD中,BC=2AB,点E为边BC的中点. 求证:AE⊥ED.
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,
AB=CD.
1
A
B
C
D
E
2
5
3
6
4
∴∠2=∠3,
∠1=∠6.
∵ BC=2AB,
∴BC=2CD,
∵点E为边BC的中点,
∴BC=2BE,
BC=2CE,
∴AB=BE,
CE=CD.
∴∠5=∠6,
∠4=∠3.
∴∠1=∠5,
∠2=∠4.
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,
AB=CD.
1
A
B
C
D
E
2
5
3
6
4
∴∠2=∠3,
∠1=∠6.
∵ BC=2AB,
∴BC=2CD,
∵点E为边BC的中点,
∴BC=2BE,
BC=2CE,
∴AB=BE,
CE=CD.
∴∠5=∠6,
∠4=∠3.
∴∠1=∠5,
∠2=∠4.
∵AB∥DC,
∴∠5+∠1+∠2+∠4=180°.
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°.
∴∠AED=90°,
∴AE⊥ED.
(1) 这节课,我们学习了哪些新的认识?
谈谈你的收获.
(2) 你对平行四边形及性质有哪些认识?
课堂小结
1.如图,AD∥BC 中, ∠A =∠D=90°,
AB=1,AD=2, 则直线AD,BC之间的距离为
= .
A
B
D
C
巩固提高
2. 在□ABCD中,AB=4cm,BC=6cm.若□ABCD的高为5cm,则它的面积为 cm2.
1
20
今天作业
课本P84页第4、6题
