19.2平行四边形(4)
图片预览


文档简介
(共18张PPT)
19.2平行四边形(4)
教学目标:
1.掌握平行四边形的第一个判定定理,会综合运用
平行四边形的性质和判定进行推理和计算;
2.经历平行四边形判定定理的发现与证明过程,进
一步加深对平行四边形的认识.
教学重点:
会综合运用平行四边形的性质和判定进行推理和计算.
教学难点:
平行四边形第一个判定定理的证明与应用.
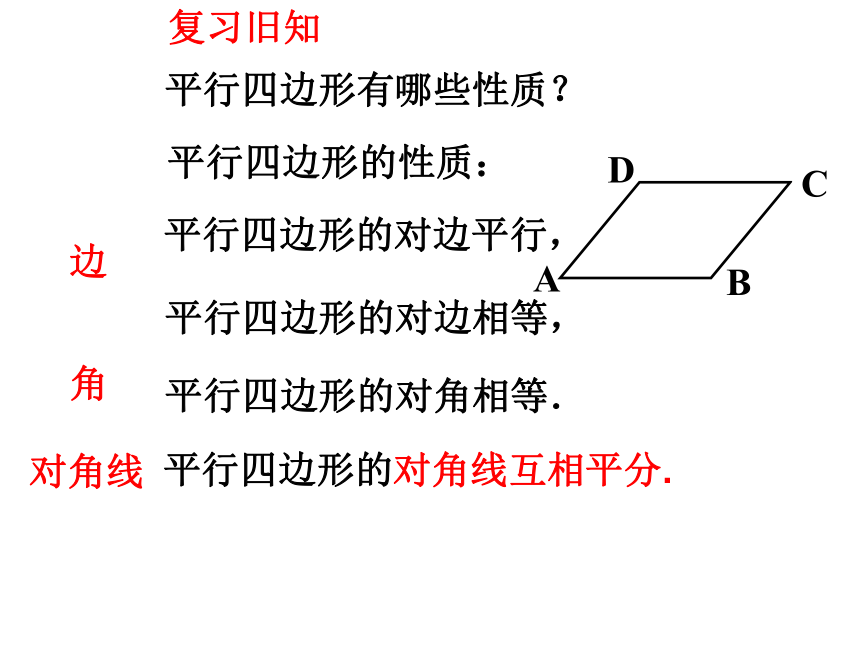
平行四边形的性质:
平行四边形的对边相等,
平行四边形的对角相等.
平行四边形的对边平行,
平行四边形的对角线互相平分.
复习旧知
平行四边形有哪些性质?
边
角
对角线
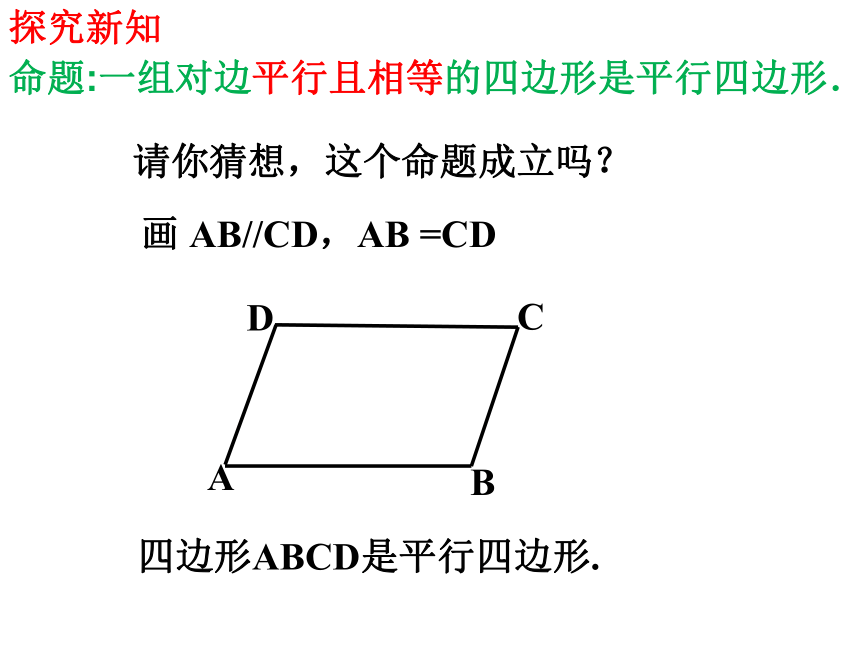
请你猜想,这个命题成立吗?
命题:一组对边平行且相等的四边形是平行四边形.
A
B
C
D
画 AB//CD,AB =CD
四边形ABCD是平行四边形.
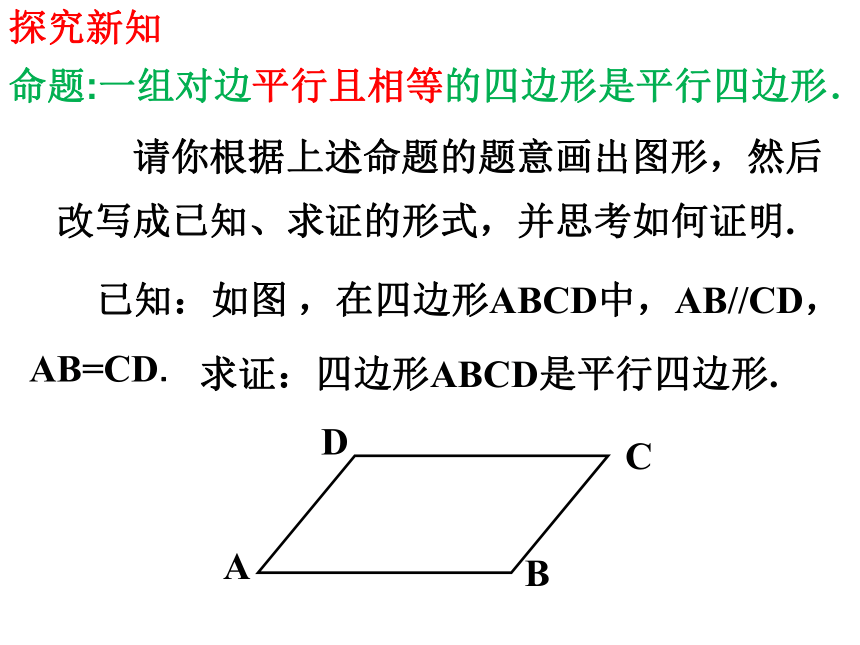
探究新知
请你根据上述命题的题意画出图形,然后改写成已知、求证的形式,并思考如何证明.
图3
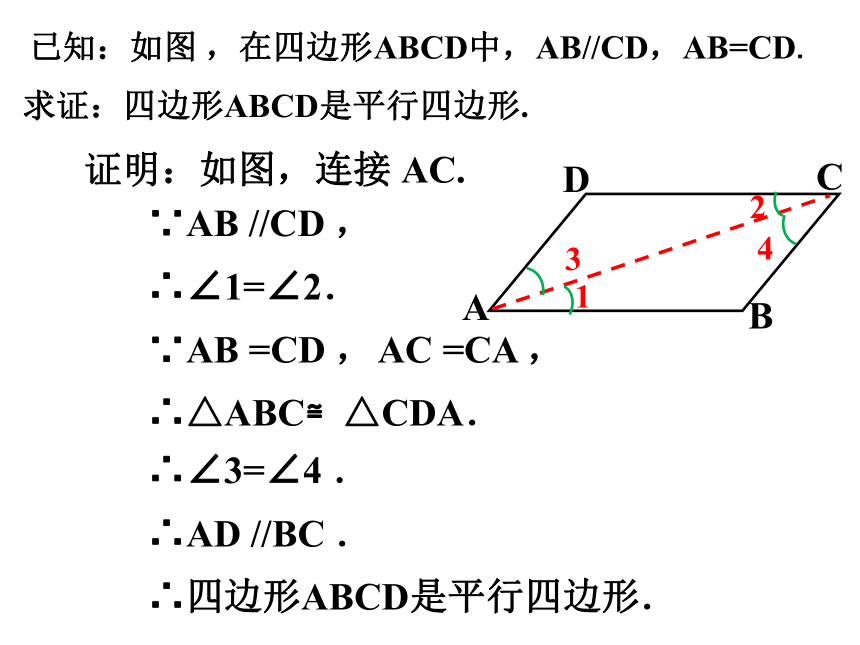
已知:如图 ,在四边形ABCD中,AB//CD,
AB=CD.
求证:四边形ABCD是平行四边形.
命题:一组对边平行且相等的四边形是平行四边形.
探究新知
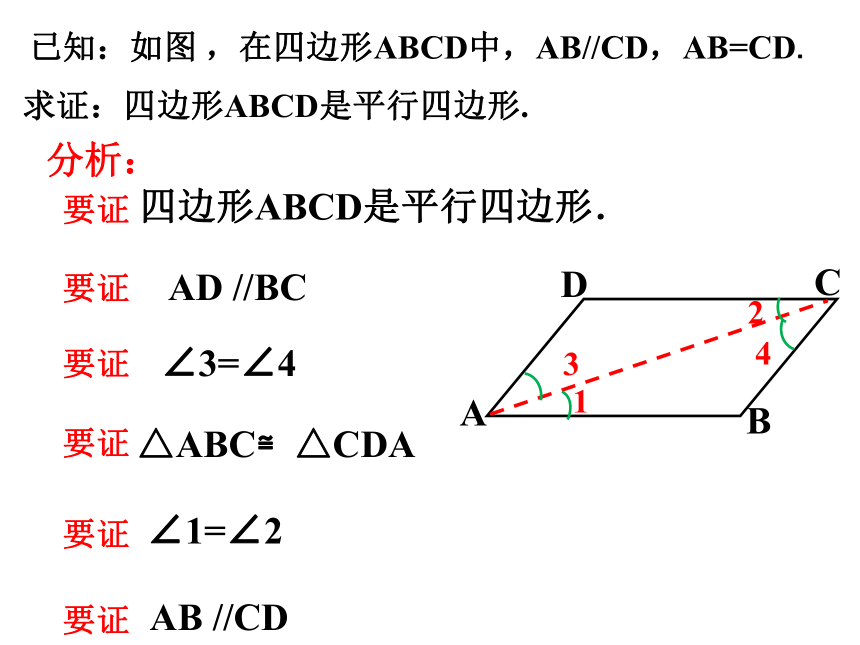
分析:
AB //CD
∠1=∠2
△ABC≌△CDA
AD //BC
∠3=∠4
四边形ABCD是平行四边形.
已知:如图 ,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
1
2
3
4
要证
要证
要证
要证
要证
要证
证明:如图,连接 AC.
∵AB //CD ,
∴∠1=∠2.
∵AB =CD ,
AC =CA ,
∴△ABC≌△CDA.
∴AD //BC .
∴∠3=∠4 .
∴四边形ABCD是平行四边形.
已知:如图 ,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
1
2
3
4
平行四边形的判定定理:
在四边形ABCD中,∵AB//CD,AB =CD,
∴四边形ABCD是平行四边形.
一组对边平行且相等的四边形是平行四边形.
∥
=
平行且相等
AB CD
∥
=
读作:AB平行且等于CD.
符号语言:
形成新知
如图,已知:BE∥DF ,AF=CE,∠ADF=∠CBE.
求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
四边形DEBF是平行四边形.
BE = DF .
△ADF≌△CBE.
∠AFD =∠CEB.
EB //FD.
要证
要证
要证
要证
分析
例题解析
证明:
∵ BE∥DF ,
∴∠AFD =∠CEB.
∵ AF =CE,
∠ADC =∠CBE.
∴△ADF≌△CBE.
∴BE =DF .
∴四边形DEBF是平行四边形.
如图,已知:BE∥DF ,AF=CE,∠ADF=∠CBE.
求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
∴BE DF.
∥
=
1.如图 ,在□ABCD中,E,F分别是AB,CD的中点. 求证:四边形EBFD是平行四边形.
E
F
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,
∵EB =
CD,
∴EB=FD .
∴四边形EBFD是平行四边形.
EB //FD.
FD =
AB,
1
2
1
2
∴EB FD.
∥
=
练习巩固
2. 如图,在□ABCD中, BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD.
求证:四边形AFCE是平行四边形.
要证
要证
要证
要证
要证
四边形AFCE是平行四边形.
AE=CF
AE∥CF
△ABE≌△CDF
AB=CD
∠ABD =∠CDB.
四边形ABCD是平行四边形.
∠AEB =∠CFD
AE⊥BD,
CF⊥BD.
E
F
1
2
E
F
1
2
∵四边形ABCD是平行四边形,
∴AB= CD,
AB∥CD.
∴∠1=∠2.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD,
∴△AEB≌△CFD.
AE //CF .
∴AE = CF .
∴四边形AECF是平行四边形.
证明:
(AAS)
∴AE CF.
∥
=
(1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)你有什么新的体会?
课堂小结
巩固提高
1.下列条件中,可以判定四边形是
平行四边形的是( ).
A.一组对边平行 B.一组对边相等
C.一组对边平行,一组对边相等
D.一组对边平行且相等
2.已知,在四边形ABCD中,AB//CD,
且AB=3x-2,CD=x+6.当x= 时,
四边形ABCD是平行四边形.
D
4
3.已知:如图 ,四边形ABCD和AEFD都是
平行四边形,则四边形BCFE是 ,
理由是 .
F
E
平行四边形
一组对边平行且相等四边形是平行四边形
4.如图,已知:AB∥CD ,BE⊥AD ,垂足为点E ,CF⊥AD ,垂足为点F ,并且 AE=DF.
求证:四边形 BECF是平行四边形.
A
B
C
D
E
F
∵ AB∥CD,
∴∠A=∠D.
证明:
∵BE⊥AD,CF⊥AD,
∴∠AEB=∠CFD=90°,
BE //CF .
∵ AE=DF,
∴△AEB≌△CFD.
∴BE = CF .
∴BE CF.
∥
=
∴四边形 BECF是平行四边形.
今天作业
课本P85页第9、10题
19.2平行四边形(4)
教学目标:
1.掌握平行四边形的第一个判定定理,会综合运用
平行四边形的性质和判定进行推理和计算;
2.经历平行四边形判定定理的发现与证明过程,进
一步加深对平行四边形的认识.
教学重点:
会综合运用平行四边形的性质和判定进行推理和计算.
教学难点:
平行四边形第一个判定定理的证明与应用.
平行四边形的性质:
平行四边形的对边相等,
平行四边形的对角相等.
平行四边形的对边平行,
平行四边形的对角线互相平分.
复习旧知
平行四边形有哪些性质?
边
角
对角线
请你猜想,这个命题成立吗?
命题:一组对边平行且相等的四边形是平行四边形.
A
B
C
D
画 AB//CD,AB =CD
四边形ABCD是平行四边形.
探究新知
请你根据上述命题的题意画出图形,然后改写成已知、求证的形式,并思考如何证明.
图3
已知:如图 ,在四边形ABCD中,AB//CD,
AB=CD.
求证:四边形ABCD是平行四边形.
命题:一组对边平行且相等的四边形是平行四边形.
探究新知
分析:
AB //CD
∠1=∠2
△ABC≌△CDA
AD //BC
∠3=∠4
四边形ABCD是平行四边形.
已知:如图 ,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
1
2
3
4
要证
要证
要证
要证
要证
要证
证明:如图,连接 AC.
∵AB //CD ,
∴∠1=∠2.
∵AB =CD ,
AC =CA ,
∴△ABC≌△CDA.
∴AD //BC .
∴∠3=∠4 .
∴四边形ABCD是平行四边形.
已知:如图 ,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
1
2
3
4
平行四边形的判定定理:
在四边形ABCD中,∵AB//CD,AB =CD,
∴四边形ABCD是平行四边形.
一组对边平行且相等的四边形是平行四边形.
∥
=
平行且相等
AB CD
∥
=
读作:AB平行且等于CD.
符号语言:
形成新知
如图,已知:BE∥DF ,AF=CE,∠ADF=∠CBE.
求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
四边形DEBF是平行四边形.
BE = DF .
△ADF≌△CBE.
∠AFD =∠CEB.
EB //FD.
要证
要证
要证
要证
分析
例题解析
证明:
∵ BE∥DF ,
∴∠AFD =∠CEB.
∵ AF =CE,
∠ADC =∠CBE.
∴△ADF≌△CBE.
∴BE =DF .
∴四边形DEBF是平行四边形.
如图,已知:BE∥DF ,AF=CE,∠ADF=∠CBE.
求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
∴BE DF.
∥
=
1.如图 ,在□ABCD中,E,F分别是AB,CD的中点. 求证:四边形EBFD是平行四边形.
E
F
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,
∵EB =
CD,
∴EB=FD .
∴四边形EBFD是平行四边形.
EB //FD.
FD =
AB,
1
2
1
2
∴EB FD.
∥
=
练习巩固
2. 如图,在□ABCD中, BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD.
求证:四边形AFCE是平行四边形.
要证
要证
要证
要证
要证
四边形AFCE是平行四边形.
AE=CF
AE∥CF
△ABE≌△CDF
AB=CD
∠ABD =∠CDB.
四边形ABCD是平行四边形.
∠AEB =∠CFD
AE⊥BD,
CF⊥BD.
E
F
1
2
E
F
1
2
∵四边形ABCD是平行四边形,
∴AB= CD,
AB∥CD.
∴∠1=∠2.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD,
∴△AEB≌△CFD.
AE //CF .
∴AE = CF .
∴四边形AECF是平行四边形.
证明:
(AAS)
∴AE CF.
∥
=
(1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)你有什么新的体会?
课堂小结
巩固提高
1.下列条件中,可以判定四边形是
平行四边形的是( ).
A.一组对边平行 B.一组对边相等
C.一组对边平行,一组对边相等
D.一组对边平行且相等
2.已知,在四边形ABCD中,AB//CD,
且AB=3x-2,CD=x+6.当x= 时,
四边形ABCD是平行四边形.
D
4
3.已知:如图 ,四边形ABCD和AEFD都是
平行四边形,则四边形BCFE是 ,
理由是 .
F
E
平行四边形
一组对边平行且相等四边形是平行四边形
4.如图,已知:AB∥CD ,BE⊥AD ,垂足为点E ,CF⊥AD ,垂足为点F ,并且 AE=DF.
求证:四边形 BECF是平行四边形.
A
B
C
D
E
F
∵ AB∥CD,
∴∠A=∠D.
证明:
∵BE⊥AD,CF⊥AD,
∴∠AEB=∠CFD=90°,
BE //CF .
∵ AE=DF,
∴△AEB≌△CFD.
∴BE = CF .
∴BE CF.
∥
=
∴四边形 BECF是平行四边形.
今天作业
课本P85页第9、10题
