19.2平行四边形(5)
图片预览





文档简介
(共24张PPT)
19.2平行四边形(5)
教学目标:
1.经历平行四边形判定定理的猜想与证明过程,体
会类比思想及探究图形判定的一般思路;
2.掌握平行四边形的三个判定定理,能根据不同条
件灵活选取适当的判定定理进行推理.
教学重点:
平行四边形三个判定定理的探究与应用.
教学难点:
根据不同条件灵活选取适当的判定定理进行推理.
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理:
复习旧知
1.平行四边形的定义是什么?
2.平行四边形的对边具有什么性质?
3.它的逆命题是什么?
你认为它成立吗?
两组对边分别平行的四边形是平行四边形.
平行四边形的两组对边分别相等.
两组对边分别相等的四边形是平行四边形.
探究新知
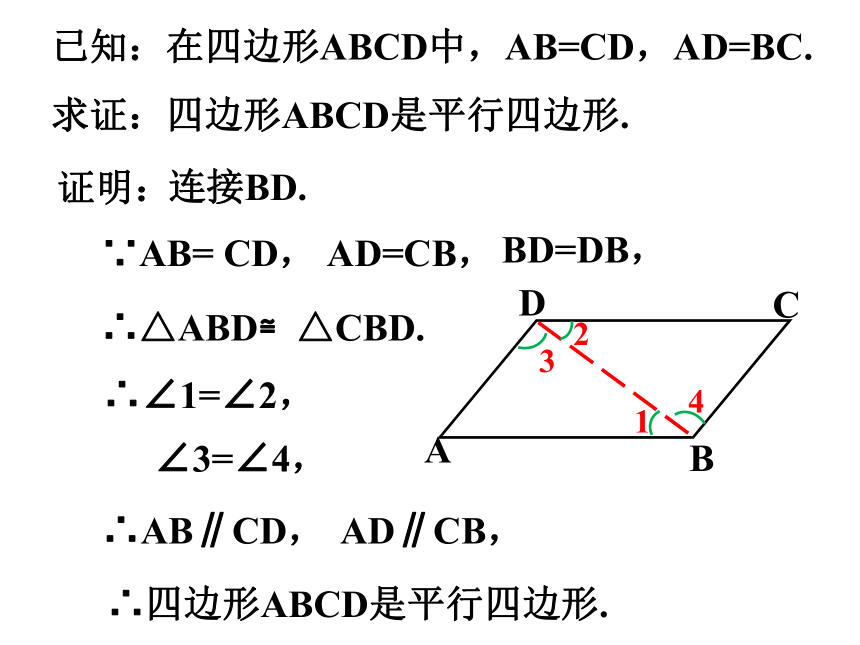
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:
连接BD.
∵AB= CD, AD=CB,
BD=DB,
∴△ABD≌△CBD.
∴∠1=∠2,
∠3=∠4,
∴四边形ABCD是平行四边形.
∴AB∥CD,
AD∥CB,
1
2
3
4
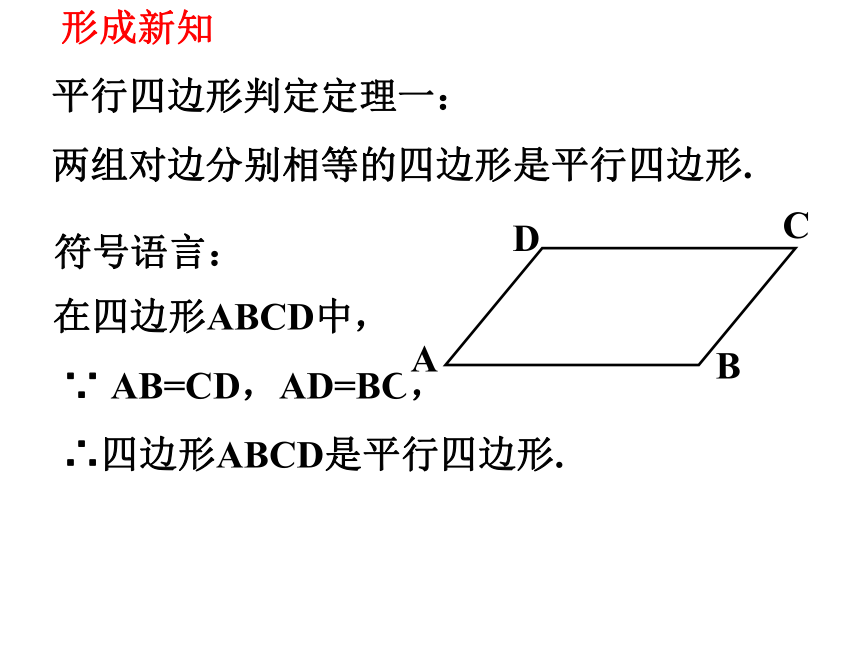
在四边形ABCD中,
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
平行四边形判定定理一:
两组对边分别相等的四边形是平行四边形.
形成新知
符号语言:
4.平行四边形的对角具有什么性质?
5.它的逆命题是什么?
你认为它成立吗?
平行四边形的两组对角分别相等.
两组对角分别相等的四边形是平行四边形.
探究新知
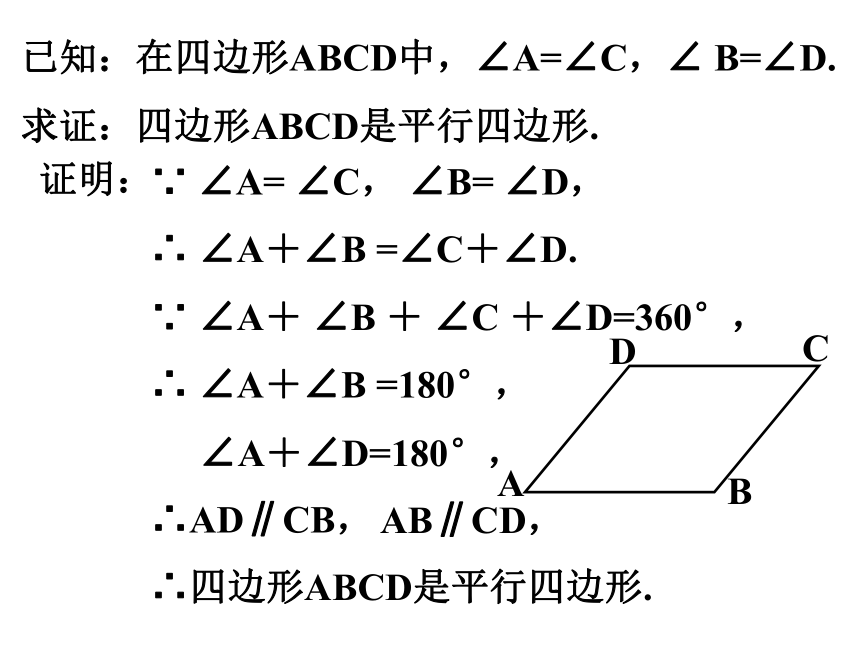
∵ ∠A= ∠C, ∠B= ∠D,
∴ ∠A+∠B =∠C+∠D.
∵ ∠A+ ∠B + ∠C +∠D=360°,
∴ ∠A+∠B =180°,
∠A+∠D=180°,
证明:
∴四边形ABCD是平行四边形.
∴AD∥CB,
AB∥CD,
已知:在四边形ABCD中,∠A=∠C,∠ B=∠D.
求证:四边形ABCD是平行四边形.
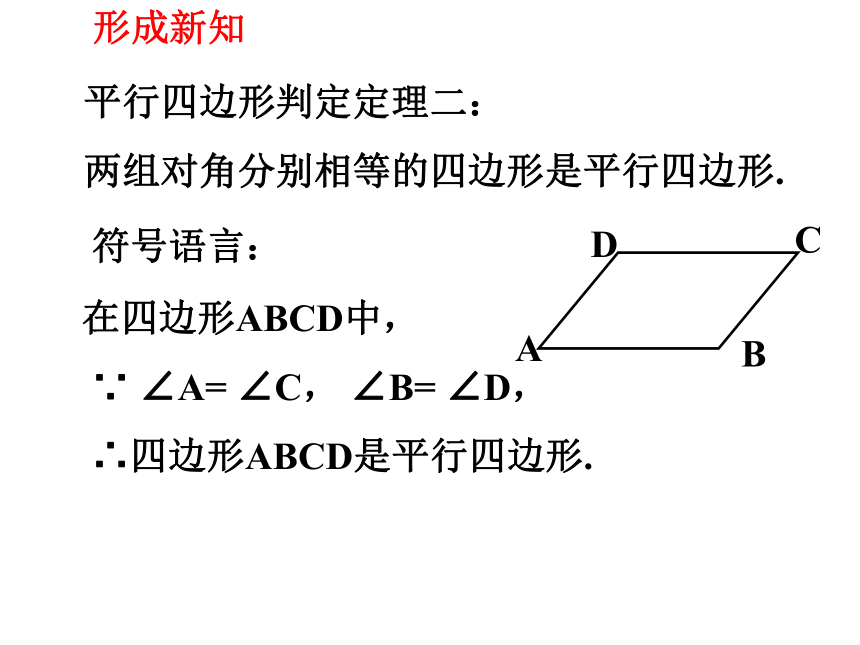
平行四边形判定定理二:
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵ ∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形.
形成新知
符号语言:
6.平行四边形的对角线具有什么性质?
5.它的逆命题是什么?
你认为它成立吗?
平行四边形的对角线互相平分.
对角线互相平分的四边形是平行四边形.
探究新知
证 明:
∵OA= OC, OB=OD,
∠AOB=∠COD,
∴△AOB≌△COD.
∴AB= CD,
∴四边形ABCD是平行四边形.
同理可证 AD=CB,
如图,四边形ABCD的对角线AC、BD交于点O.
且 OA= OC, OB=OD.
求证:四边形ABCD是平行四边形.
O
平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.
∵ OA= OC, OB=OD,
∴四边形ABCD是平行四边形.
O
符号语言:
形成新知
两组对边分别平行的四边形是平行四边形
平形四边形的判定定理
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
归纳小结
例5 如图, 点E,F是□ABCD的对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴OA= OC,
∵AE=CF,
∴OA-AE=OC-CF.
∴OE=OF.
∴四边形BFDE是平行四边形.
证明:
OB=OD.
E
F
O
连接BD,
交AC于点O.
例题解析
例6 如图, 直线l1,l2,l3互相平行,直线AC和直线A1C1分别交直线l1,l2,l3于点A,B,C和点A1,B1,C1,且AB=BC.
求证:A1B1=B1C1.
A
B
C
A1
B1
C1
l1
l2
l3
A
C
B
例题解析
探究
例6 如图, 直线l1,l2,l3互相平行,直线AC和直线A1C1分别交直线l1,l2,l3于点A,B,C和点A1,B1,C1,且AB=BC.
求证:A1B1=B1C1.
A
B
C
A1
B1
C1
l1
l2
l3
E
F
过点B1作EF∥AC,
分别交直线l1,l3
于点E,F.
过点B1作EF∥AC,
A
B
C
A1
B1
C1
l1
l2
l3
E
F
分别交l1,l3于点E,F.
证明:
∵l1∥l2, AB∥EB1,
∴AB= EB1.
∵l2∥l3, BC∥FB1,
∴BC= B1F.
∵AB=BC,
∴EB1= FB1.
∵l1∥l3,
∴∠A1EB1=∠B1FC1.
∵∠A1B1E =∠FB1C1,
∴△A1B1E ≌△C1B1F
∴A1B1= C1B1.
例6 如图, 直线l1,l2,l3互相平行,直线AC和直线A1C1分别交直线l1,l2,l3于点A,B,C和点A1,B1,C1,且AB=BC.
求证:A1B1=B1C1.
A
B
C
A1
B1
C1
l1
l2
l3
E
F
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
经过三角形一边中点与另一边平行的直线必平分第三边.
A
B
C
A1
B1
C1
l1
l2
l3
推论
A
B
C
D
E
∵AD=DB,
DE∥BC,
∴AE= CE.
证明:
∴四边形ABCD是平行四边形.
∴AB∥DC.
又∵DC=EF,
∴四边形DCFE也是平行四边形.
∴DC∥EF. ∴AB∥EF.
如图,AB=DC=EF,AD=BC,DE=CF.
求证:AB∥EF.
A
B
C
D
E
F
AD=BC,
∵AB=DC,
DE=CF,
练习巩固
平行四边形的判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
课堂小结
1.下列条件中,不能判定四边形是
平行四边形的是( ).
A.两组对边分别平行
B.两组对边分别相等
C.一组对边平行另一组对边相等
D.一组对边平行且相等
C
巩固提高
2.如图,在□ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.若AB=5cm,则BF= cm.
D
C
F
B
A
E
5
今天作业
课本P85页第9、10、11题
19.2平行四边形(5)
教学目标:
1.经历平行四边形判定定理的猜想与证明过程,体
会类比思想及探究图形判定的一般思路;
2.掌握平行四边形的三个判定定理,能根据不同条
件灵活选取适当的判定定理进行推理.
教学重点:
平行四边形三个判定定理的探究与应用.
教学难点:
根据不同条件灵活选取适当的判定定理进行推理.
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理:
复习旧知
1.平行四边形的定义是什么?
2.平行四边形的对边具有什么性质?
3.它的逆命题是什么?
你认为它成立吗?
两组对边分别平行的四边形是平行四边形.
平行四边形的两组对边分别相等.
两组对边分别相等的四边形是平行四边形.
探究新知
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:
连接BD.
∵AB= CD, AD=CB,
BD=DB,
∴△ABD≌△CBD.
∴∠1=∠2,
∠3=∠4,
∴四边形ABCD是平行四边形.
∴AB∥CD,
AD∥CB,
1
2
3
4
在四边形ABCD中,
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
平行四边形判定定理一:
两组对边分别相等的四边形是平行四边形.
形成新知
符号语言:
4.平行四边形的对角具有什么性质?
5.它的逆命题是什么?
你认为它成立吗?
平行四边形的两组对角分别相等.
两组对角分别相等的四边形是平行四边形.
探究新知
∵ ∠A= ∠C, ∠B= ∠D,
∴ ∠A+∠B =∠C+∠D.
∵ ∠A+ ∠B + ∠C +∠D=360°,
∴ ∠A+∠B =180°,
∠A+∠D=180°,
证明:
∴四边形ABCD是平行四边形.
∴AD∥CB,
AB∥CD,
已知:在四边形ABCD中,∠A=∠C,∠ B=∠D.
求证:四边形ABCD是平行四边形.
平行四边形判定定理二:
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵ ∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形.
形成新知
符号语言:
6.平行四边形的对角线具有什么性质?
5.它的逆命题是什么?
你认为它成立吗?
平行四边形的对角线互相平分.
对角线互相平分的四边形是平行四边形.
探究新知
证 明:
∵OA= OC, OB=OD,
∠AOB=∠COD,
∴△AOB≌△COD.
∴AB= CD,
∴四边形ABCD是平行四边形.
同理可证 AD=CB,
如图,四边形ABCD的对角线AC、BD交于点O.
且 OA= OC, OB=OD.
求证:四边形ABCD是平行四边形.
O
平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.
∵ OA= OC, OB=OD,
∴四边形ABCD是平行四边形.
O
符号语言:
形成新知
两组对边分别平行的四边形是平行四边形
平形四边形的判定定理
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
归纳小结
例5 如图, 点E,F是□ABCD的对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴OA= OC,
∵AE=CF,
∴OA-AE=OC-CF.
∴OE=OF.
∴四边形BFDE是平行四边形.
证明:
OB=OD.
E
F
O
连接BD,
交AC于点O.
例题解析
例6 如图, 直线l1,l2,l3互相平行,直线AC和直线A1C1分别交直线l1,l2,l3于点A,B,C和点A1,B1,C1,且AB=BC.
求证:A1B1=B1C1.
A
B
C
A1
B1
C1
l1
l2
l3
A
C
B
例题解析
探究
例6 如图, 直线l1,l2,l3互相平行,直线AC和直线A1C1分别交直线l1,l2,l3于点A,B,C和点A1,B1,C1,且AB=BC.
求证:A1B1=B1C1.
A
B
C
A1
B1
C1
l1
l2
l3
E
F
过点B1作EF∥AC,
分别交直线l1,l3
于点E,F.
过点B1作EF∥AC,
A
B
C
A1
B1
C1
l1
l2
l3
E
F
分别交l1,l3于点E,F.
证明:
∵l1∥l2, AB∥EB1,
∴AB= EB1.
∵l2∥l3, BC∥FB1,
∴BC= B1F.
∵AB=BC,
∴EB1= FB1.
∵l1∥l3,
∴∠A1EB1=∠B1FC1.
∵∠A1B1E =∠FB1C1,
∴△A1B1E ≌△C1B1F
∴A1B1= C1B1.
例6 如图, 直线l1,l2,l3互相平行,直线AC和直线A1C1分别交直线l1,l2,l3于点A,B,C和点A1,B1,C1,且AB=BC.
求证:A1B1=B1C1.
A
B
C
A1
B1
C1
l1
l2
l3
E
F
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
经过三角形一边中点与另一边平行的直线必平分第三边.
A
B
C
A1
B1
C1
l1
l2
l3
推论
A
B
C
D
E
∵AD=DB,
DE∥BC,
∴AE= CE.
证明:
∴四边形ABCD是平行四边形.
∴AB∥DC.
又∵DC=EF,
∴四边形DCFE也是平行四边形.
∴DC∥EF. ∴AB∥EF.
如图,AB=DC=EF,AD=BC,DE=CF.
求证:AB∥EF.
A
B
C
D
E
F
AD=BC,
∵AB=DC,
DE=CF,
练习巩固
平行四边形的判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
课堂小结
1.下列条件中,不能判定四边形是
平行四边形的是( ).
A.两组对边分别平行
B.两组对边分别相等
C.一组对边平行另一组对边相等
D.一组对边平行且相等
C
巩固提高
2.如图,在□ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.若AB=5cm,则BF= cm.
D
C
F
B
A
E
5
今天作业
课本P85页第9、10、11题
