北京市第九中学2023-2024学年高二下学期4月月考数学试卷(含答案)
文档属性
| 名称 | 北京市第九中学2023-2024学年高二下学期4月月考数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 995.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 20:09:01 | ||
图片预览




文档简介
2024北京九中高二4月月考
数学
2024.4
(考试时间120分钟 满分150分)
一、单选题(共40分)
1.(本题4分)从0,1,2,3,4中选出3个数组成各位数字不重复的3位偶数,这样的数有( )个.
A.24 B.30 C.36 D.60
2.(本题4分)在数列中,若,则( )
A.﹣2 B. C.1 D.4
3.(本题4分)若,则( )
A.100 B.110 C.120 D.130
4.(本题4分)已知数列的前n项和为,则( )
A.81 B.162 C.243 D.486
5.(本题4分)若的展开式中各项系数之和为﹣128,则展开式中的系数为( )
A.﹣2835 B.945 C.2835 D.﹣945
6.(本题4分)等比数列满足,则( )
A.56 B.﹣56 C.﹣112 D.112
7.(本题4分)甲、乙、丙、丁四名同学参加学校组织的植树活动,学校共组织了3个植树小组,每人只能参加一个植树小组,则甲、乙不在同一个植树小组的安排方法有( )
A.81种 B.54种 C.36种 D.12种
8.(本题4分)在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1可能被错误的接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号为1时,接收为1和0的概率分别为p和.假设发送信号0和1是等可能的.已知接收到1的概率为0.475,则p的值为( )
A.0.8 B.0.85 C.0.9 D.0.95
9.(本题4分)排球比赛实行“每球得分制”,即每次发球后,谁取胜谁就得1分,得分的队有发球权,最后先得25分的队获得本局比赛胜利,若出现比分24:24,要继续比赛至某队领先2分才能取胜,该局比赛结束.甲、乙两队进行一局排球比赛,已知甲队发球时甲队获胜的概率为,乙队发球时甲队获胜的概率为,且各次发球的胜负结果相互独立.若此时甲、乙两队双方比分为22:22平,且甲队拥有发球权,则甲队得25分且取得该局比赛胜利的概率为( )
A. B. C. D.
10.(本题4分)已知是数列的前n项和,且,,则下列结论正确的是( )
A.数列为等比数列 B.数列为等比数列
C. D.
二、填空题(共25分)
11.(本题5分)在数列中,若,则的值为______.
12.(本题5分)在等差数列中,,则的前10项和______.
13.(本题5分)已知甲、乙两人投篮的命中率分别为0.5和0.8,且两人投篮相互没有影响.若投进一球得2分,未进得0分,则每人投篮一次,得分相等的概率为______.
14.(本题5分)如图,在由二项式系数所构成的杨辉三角形中,第10行中最大的数与第二大的数的数值之比为______(用最简分数表示).
15.(本题5分)已知数列:1,1,2,1,2,4,1,2,4,8,…,其中第一项是,接下来的两项是,再接下来的三项是,…,以此类推,则下列说法正确的是______.
①第10个1出现在第46项;
②该数列的前55项的和是1012;
③存在连续六项之和是3的倍数;
④满足前n项之和为2的整数幂,且n>100的最小整数n的值为440
三、解答题(共85分)
16.(本题13分)已知在等差数列中,.
(1)求数列的通项公式;
(2)若数列的前n项和,则当n为何值时取得最大,并求出此最大值.
17.(本题13分)已知公差不为0的等差数列的前n项和为,且,成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
18.(本题15分)国务院正式公布的《第一批全国重点文物保护单位名单》中把全国重点文物保护单位(下述简称为“第一批文保单位”)分为六大类.其中“A:革命遗址及革命纪念建筑物”、“B:石窟寺”、“C:古建筑及历史纪念建筑物”、“D:石刻及其他”、“E:古遗址”、“F:古墓群”,某旅行机构统计到北京部分区的17个“第一批文保单位”所在区分布如下表:
行政区 门类 个数
东城区 A:革命遗址及革命纪念建筑物 3
C:古建筑及历史纪念建筑物 5
西城区 C:古建筑及历史纪念建筑物 2
丰台区 A:革命遗址及革命纪念建筑物 1
海淀区 C:古建筑及历史纪念建筑物 2
房山区 C:古建筑及历史纪念建筑物 1
E:古遗址 1
昌平区 C:古建筑及历史纪念建筑物 1
F:古墓葬 1
(1)某个研学小组随机选择该旅行社统计的北京市17个“第一批文保单位”中的一个进行参观,求选中的参观单位恰好为“C:古建筑及历史纪念建筑物”的概率;
(2)小王同学随机选择该机构统计到的北京市“第一批文保单位”中的“A:革命遗址及革命纪念建筑物”中的一个进行参观;小张同学随机选择统计到的北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中的一个进行参观,两人选择参观单位互不影响,求两人选择的参观单位恰好在同一个区的概率:
(3)现在拟从该机构统计到的北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中随机抽取2个单位进行常规检查.记抽到海淀区的概率为,抽不到海淀区的概率为,试判断和的大小(直接写出结论).
19.(本题14分)已知数列的前n项和为,且满足.
(1)求数列的通项公式;
(2)设,数列的前n项和为,求证.
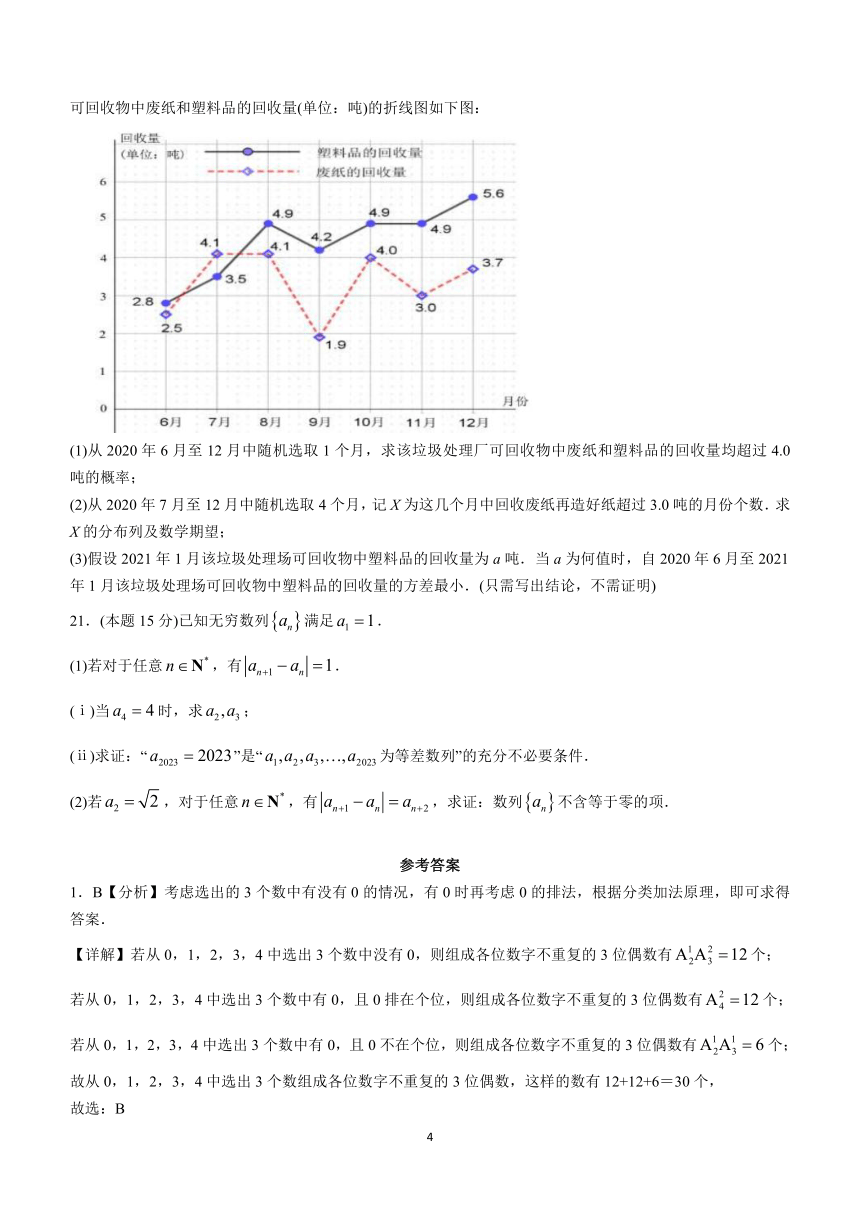
20.(本题15分)2020年5月1日起,北京市实行生活垃圾分类,分类标准为厨余垃圾、可回收物、有害垃圾和其它垃圾四类.生活垃圾中有一部分可以回收利用,回收1吨废纸可再造出0.8吨好纸,降低造纸的污染排放,节省造纸能源消耗.某环保小组调查了北京市某垃圾处理场2020年6月至12月生活垃圾回收情况,其中可回收物中废纸和塑料品的回收量(单位:吨)的折线图如下图:
(1)从2020年6月至12月中随机选取1个月,求该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨的概率;
(2)从2020年7月至12月中随机选取4个月,记X为这几个月中回收废纸再造好纸超过3.0吨的月份个数.求X的分布列及数学期望;
(3)假设2021年1月该垃圾处理场可回收物中塑料品的回收量为a吨.当a为何值时,自2020年6月至2021年1月该垃圾处理场可回收物中塑料品的回收量的方差最小.(只需写出结论,不需证明)
21.(本题15分)已知无穷数列满足.
(1)若对于任意,有.
(ⅰ)当时,求;
(ⅱ)求证:“”是“为等差数列”的充分不必要条件.
(2)若,对于任意,有,求证:数列不含等于零的项.
参考答案
1.B【分析】考虑选出的3个数中有没有0的情况,有0时再考虑0的排法,根据分类加法原理,即可求得答案.
【详解】若从0,1,2,3,4中选出3个数中没有0,则组成各位数字不重复的3位偶数有个;
若从0,1,2,3,4中选出3个数中有0,且0排在个位,则组成各位数字不重复的3位偶数有个;
若从0,1,2,3,4中选出3个数中有0,且0不在个位,则组成各位数字不重复的3位偶数有个;故从0,1,2,3,4中选出3个数组成各位数字不重复的3位偶数,这样的数有12+12+6=30个,
故选:B
2.A【分析】根据给定条件,探求出数列的周期,再利用周期性计算即得.
【详解】在数列中,由,得,
因此数列是周期性数列,周期为3,所以.故选:A
3.C【分析】利用二项式定理分别求出,即可计算得解.
【详解】在中,,
所以.故选:C
4.B【分析】根据给定条件,利用列式计算即得.
【详解】数列的前n项和为,所以.故选:B
5.D【分析】根据赋值法求系数和得,即可根据展开式的通项公式求解.
【详解】令,得,得,
则的展开式的通项,
令,得r=3,则,故展开式中的系数为﹣945,故选:D.
6.D【分析】根据等比数列的定义解决问题.
【详解】由题意知,解得,
故.故选:D.
7.B【分析】根据分步计数原理分析求解即可.
【详解】甲有3种参加方法,乙有2种参加方法,丙、丁均有3种参加方法,根据分步乘法计数原理可知,甲、乙不在同一个植树小组的安排方法有3×2×3×3=54种,故选:B.
8.B【分析】利用全概率公式计算可得.
【详解】设A=“发送的信号为0”,B=“接收到的信号为0”,
则“发送的信号为1”,“接收到的信号为1”,
所以,
所以接收信号为1的概率为:,
解得p=0.85,故选:B.
9.C【分析】甲队得25分且取得该局比赛胜利包含甲以25:22取得比赛胜利和甲以25:23取得胜利两个事件,再利用事件的相互独立性及互斥事件加法公式求概率.
【详解】记事件A=“甲队得25分且取得该局比赛胜利”,
事件B=“甲以25:22取得该局胜利”,C=“甲以25:23取得该局胜利”,
因为各次发球的胜负结果相互独立,且B,C互斥,所以,
,
所以,
所以甲队得25分且取得该局比赛胜利的概率为.故选:C
10.D【分析】A选项,计算出,故不是等比数列,A错误;
B选项,计算出的前三项,得到,B错误;
C选项,由题干条件得到,故为等比数列,得到,
故,相加即可求出,C错误;
D选项,在的基础上,分奇偶项,分别得到通项公式,最后求出.
【详解】由题意得:,
由于,故数列不是等比数列,A错误;
则,
由于,故数列不为等比数列,B错误;
时,,即,
又,
故为等比数列,首项为2,公比为3,
故,
故,
以上20个式子相加得:,C错误;
因为,所以,两式相减得:
,
当时,
以上式子相加得:,
故,而也符和该式,故,
令得:,
当时,
以上式子相加得:,
故,而也符号该式,故,
令得:,综上:,D正确.故选:D
【点睛】当遇到时,数列往往要分奇数项和偶数项,分别求出通项公式,最后再检验能不能合并为一个,这类题目的处理思路可分别令和,用累加法进行求解.
11.17 【分析】将,时分别代入偶数与奇数对应通项,即可求解.
【详解】依题意,.故答案为:17
12.155 【分析】由等差数列求和公式即可得解.
【详解】由题意.故答案为:155.
13.0.5/
【分析】根据独立事件同时发生的概率公式,即可求解.
【详解】若两人都没有投进,概率,
若两人都投进,概率,
则得分相等的概率.故答案为:0.5
14. 【分析】第10行从左至右依次为,,,…,,由二项式系数性质可得答案.
【详解】观察知第10行从左至右依次为,,,…,,
由二项式系数的性质可得最大,其次为,
所以第10行中最大的数与第二大的数的数值之比为.故答案为:.
15.①③④
【分析】把题设中的数列分成如下的组:(1),(1,2),(1,2,4),(1,2,4,8),…,求出每组的和为,命题①通过计算每组项数的和求解;命题②恰好是前10组之和;命题③通过找到符合题意得出判断;命题④设前n项由前k行和第k+1行前,项组成,算出前n和为后结合前n项和为2的整数幂可得n的最小值.
【详解】将数列排成行的形式
1,
1,2,
1,2,4,
1,2,4,8,
…
第行为:,则第k行和为,
前k行共有个数,前k行的和为,
对于命题①,第10个1出现在第1+2+3+4+5+6+7+8+9+1=46项,故①正确;
对于命题②,因为,所以数列的前55项的和是,故②错误;
对于命题③,因为,是3的倍数,所以存在连续六项之和是3的倍数,故③正确;
对于命题④,设前n项由前k行和第k+1行前项组成,则.
前n项和为,若前n项和为2的整数幂,则有,即.
因为,所以当时,;
当时,;
当时,;
当时,;
所以满足前n项之和为2的整数幂,且n>100的最小整数n的值为440,故④正确.
故答案为:①③④
【点睛】关键点点睛:本题考查分组数列的和以及与不定方程的整数解,对于分组数列的前n项和的问题,一般采用计算“大组”和,再计算“小组”和,而不定方程的整数解问题,则需把和式放缩为2的正整数幂的形式,从而确定和的表达式.
16.(1);
(2)时取得最大值为36.
【分析】(1)根据已知及等差数列通项公式求基本量,进而写出通项公式;
(2)写出等差数列前n项和,应用其二次函数性质求最大值和对应n.
【详解】(1)设等差数列的公差为d,则,
故,所以.
(2)由,且,
所以,
故n=6时取得最大,最大值为36.
17.(1);(2).
【分析】(1)设等差数列的公差为d,根据题意列出关于和d的方程组求解即可;
(2)证明是等比数列,根据等比数列前n项和公式即可求解.
【详解】(1)设等差数列的公差为,
∵成等比数列,
解得
∴;
(2)由(1)得,,
∴,
∴是首项为4,公比为4的等比数列,
∴.
18.(1) (2) (3)
【分析】(1)由题意知总样本数为17,C:古建筑及历史纪念建筑物共有11,利用古典概型概率公式从而求解.
(2)由题意可知小王参观A:革命遗址及革命纪念建筑物与小张参观C:古建筑及历史纪念建筑物在同一个区的只有东城区,然后分别求出他们参观东城区的概率,从而求解.
(3)利用分类讨论求出抽到海淀区的概率和抽不到海淀区的概率,从而求解.
【详解】(1)设选中参观单位恰好为“C:古建筑及历史纪念建筑物”为事件C,
由题意知总共有17个,“C:古建筑及历史纪念建筑物”有11,所以.
(2)设两人选择的参观单位恰好在同一个区为事件B,由题意可知小王参观A:革命遗址及革命纪念建筑物与小张参观C:古建筑及历史纪念建筑物在同一个区的只有东城区,
所以小王参观东城区景区的概率为,小张参观东城区景区的概率为.
所以.
(3)当抽到的2个都是海淀区的概率为,
当抽到的2个中有1个是海淀区的概率为,
所以,所以.
19.(1)
(2)证明见解析
【分析】(1)由与的关系结合等比数列的定义、通项计算即可;
(2)利用等差数列求和公式结合裂项相消法证明不等式即可.
【详解】(1)由已知,
又,即是以3为首项和公比的等比数列,
即;
(2)由(1)可知,所以,
则,
因为,显然,则,证毕.
20.(1) (2)分布列见解析, (3)4.4
【分析】(1)记“该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨”为事件A,推出只有8月份的可回收物中废纸和塑料品的回收量均超过4.0吨,然后求解概率.
(2)X的所有可能取值为1,2,3,利用超几何概率公式求出概率得到分布列,然后求解期望即可.
(3)根据方差的计算公式,结合二次函数的性质即可求解最小值.
【详解】(1)记“该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨”为事件A由题意,只有8月份的可回收物中废纸和塑料品的回收量均超过4.0吨 所以
(2)因为回收利用1吨废纸可再造出0.8吨好纸
所以7月至12月回收的废纸可再造好纸超过3.0吨的月份有:7月、8月、10月,共3个月.
X的所有可能取值为1,2,3.
,,
所以X的分布列为:
X 0 1 2
P
(3),当添加的新数a等于原几个数的平均值时,方差最小.
理由如下:由于2020年6月至2020年12月该垃圾处理场可回收物中塑料品的回收量分别为2.8,3.5,4.9,4.2,4.9,4.9,5.6,故其平均数为
2020年6月至2021年1月该垃圾处理场可回收物中塑料品的回收量方差为
,
其中为2020年6月至2020年12月该垃圾处理场可回收物中塑料品的回收量)
由于为定值,所以只需要取最小即可,
根据二次函数的性质可知当取最小,所以当添加的新数a等于原几个数的平均值时,方差最小.
21.(1)(ⅰ);(ⅱ)证明见解析 (2)证明见解析
【分析】(1)(ⅰ)结合条件代入计算即可;
(ⅱ)若,由于2023﹣1=2022,所以当,数列为递增数列,不能存在降低的部分,否则达不到2023,若数列的公差为﹣1,;
(2)假设为数列的第一个为0项,而后进行反证即可.
【详解】(1)解:(ⅰ)因为,所以当,
数列为递增数列,且公差为1,不能存在降低的部分,
所以.
(ⅱ)若,由于2023﹣1=2022,
所以当,数列为递增数列,且公差为1,不能存在降低的部分,
否则达不到2023,所以其是充分条件,
若数列的公差为﹣1,,可见其是不必要条件,
所以“”是“为等差数列”的充分不必要条件;
(2)证明:假设,是数列第一个为0项,则,
所以或,以此类推,可得(p,q为整数),
显然与已知矛盾.所以数列不含等于零的项.
【点睛】与数列的新定义有关的问题的求解策略:
1、通过给出一个新的数列的定义,或约定一种新的运算,或给出几个新模型来创设新问题的情景,要求在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实心信息的迁移,达到灵活解题的目的;
2、遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使得问题得以解决.
数学
2024.4
(考试时间120分钟 满分150分)
一、单选题(共40分)
1.(本题4分)从0,1,2,3,4中选出3个数组成各位数字不重复的3位偶数,这样的数有( )个.
A.24 B.30 C.36 D.60
2.(本题4分)在数列中,若,则( )
A.﹣2 B. C.1 D.4
3.(本题4分)若,则( )
A.100 B.110 C.120 D.130
4.(本题4分)已知数列的前n项和为,则( )
A.81 B.162 C.243 D.486
5.(本题4分)若的展开式中各项系数之和为﹣128,则展开式中的系数为( )
A.﹣2835 B.945 C.2835 D.﹣945
6.(本题4分)等比数列满足,则( )
A.56 B.﹣56 C.﹣112 D.112
7.(本题4分)甲、乙、丙、丁四名同学参加学校组织的植树活动,学校共组织了3个植树小组,每人只能参加一个植树小组,则甲、乙不在同一个植树小组的安排方法有( )
A.81种 B.54种 C.36种 D.12种
8.(本题4分)在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1可能被错误的接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号为1时,接收为1和0的概率分别为p和.假设发送信号0和1是等可能的.已知接收到1的概率为0.475,则p的值为( )
A.0.8 B.0.85 C.0.9 D.0.95
9.(本题4分)排球比赛实行“每球得分制”,即每次发球后,谁取胜谁就得1分,得分的队有发球权,最后先得25分的队获得本局比赛胜利,若出现比分24:24,要继续比赛至某队领先2分才能取胜,该局比赛结束.甲、乙两队进行一局排球比赛,已知甲队发球时甲队获胜的概率为,乙队发球时甲队获胜的概率为,且各次发球的胜负结果相互独立.若此时甲、乙两队双方比分为22:22平,且甲队拥有发球权,则甲队得25分且取得该局比赛胜利的概率为( )
A. B. C. D.
10.(本题4分)已知是数列的前n项和,且,,则下列结论正确的是( )
A.数列为等比数列 B.数列为等比数列
C. D.
二、填空题(共25分)
11.(本题5分)在数列中,若,则的值为______.
12.(本题5分)在等差数列中,,则的前10项和______.
13.(本题5分)已知甲、乙两人投篮的命中率分别为0.5和0.8,且两人投篮相互没有影响.若投进一球得2分,未进得0分,则每人投篮一次,得分相等的概率为______.
14.(本题5分)如图,在由二项式系数所构成的杨辉三角形中,第10行中最大的数与第二大的数的数值之比为______(用最简分数表示).
15.(本题5分)已知数列:1,1,2,1,2,4,1,2,4,8,…,其中第一项是,接下来的两项是,再接下来的三项是,…,以此类推,则下列说法正确的是______.
①第10个1出现在第46项;
②该数列的前55项的和是1012;
③存在连续六项之和是3的倍数;
④满足前n项之和为2的整数幂,且n>100的最小整数n的值为440
三、解答题(共85分)
16.(本题13分)已知在等差数列中,.
(1)求数列的通项公式;
(2)若数列的前n项和,则当n为何值时取得最大,并求出此最大值.
17.(本题13分)已知公差不为0的等差数列的前n项和为,且,成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
18.(本题15分)国务院正式公布的《第一批全国重点文物保护单位名单》中把全国重点文物保护单位(下述简称为“第一批文保单位”)分为六大类.其中“A:革命遗址及革命纪念建筑物”、“B:石窟寺”、“C:古建筑及历史纪念建筑物”、“D:石刻及其他”、“E:古遗址”、“F:古墓群”,某旅行机构统计到北京部分区的17个“第一批文保单位”所在区分布如下表:
行政区 门类 个数
东城区 A:革命遗址及革命纪念建筑物 3
C:古建筑及历史纪念建筑物 5
西城区 C:古建筑及历史纪念建筑物 2
丰台区 A:革命遗址及革命纪念建筑物 1
海淀区 C:古建筑及历史纪念建筑物 2
房山区 C:古建筑及历史纪念建筑物 1
E:古遗址 1
昌平区 C:古建筑及历史纪念建筑物 1
F:古墓葬 1
(1)某个研学小组随机选择该旅行社统计的北京市17个“第一批文保单位”中的一个进行参观,求选中的参观单位恰好为“C:古建筑及历史纪念建筑物”的概率;
(2)小王同学随机选择该机构统计到的北京市“第一批文保单位”中的“A:革命遗址及革命纪念建筑物”中的一个进行参观;小张同学随机选择统计到的北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中的一个进行参观,两人选择参观单位互不影响,求两人选择的参观单位恰好在同一个区的概率:
(3)现在拟从该机构统计到的北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中随机抽取2个单位进行常规检查.记抽到海淀区的概率为,抽不到海淀区的概率为,试判断和的大小(直接写出结论).
19.(本题14分)已知数列的前n项和为,且满足.
(1)求数列的通项公式;
(2)设,数列的前n项和为,求证.
20.(本题15分)2020年5月1日起,北京市实行生活垃圾分类,分类标准为厨余垃圾、可回收物、有害垃圾和其它垃圾四类.生活垃圾中有一部分可以回收利用,回收1吨废纸可再造出0.8吨好纸,降低造纸的污染排放,节省造纸能源消耗.某环保小组调查了北京市某垃圾处理场2020年6月至12月生活垃圾回收情况,其中可回收物中废纸和塑料品的回收量(单位:吨)的折线图如下图:
(1)从2020年6月至12月中随机选取1个月,求该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨的概率;
(2)从2020年7月至12月中随机选取4个月,记X为这几个月中回收废纸再造好纸超过3.0吨的月份个数.求X的分布列及数学期望;
(3)假设2021年1月该垃圾处理场可回收物中塑料品的回收量为a吨.当a为何值时,自2020年6月至2021年1月该垃圾处理场可回收物中塑料品的回收量的方差最小.(只需写出结论,不需证明)
21.(本题15分)已知无穷数列满足.
(1)若对于任意,有.
(ⅰ)当时,求;
(ⅱ)求证:“”是“为等差数列”的充分不必要条件.
(2)若,对于任意,有,求证:数列不含等于零的项.
参考答案
1.B【分析】考虑选出的3个数中有没有0的情况,有0时再考虑0的排法,根据分类加法原理,即可求得答案.
【详解】若从0,1,2,3,4中选出3个数中没有0,则组成各位数字不重复的3位偶数有个;
若从0,1,2,3,4中选出3个数中有0,且0排在个位,则组成各位数字不重复的3位偶数有个;
若从0,1,2,3,4中选出3个数中有0,且0不在个位,则组成各位数字不重复的3位偶数有个;故从0,1,2,3,4中选出3个数组成各位数字不重复的3位偶数,这样的数有12+12+6=30个,
故选:B
2.A【分析】根据给定条件,探求出数列的周期,再利用周期性计算即得.
【详解】在数列中,由,得,
因此数列是周期性数列,周期为3,所以.故选:A
3.C【分析】利用二项式定理分别求出,即可计算得解.
【详解】在中,,
所以.故选:C
4.B【分析】根据给定条件,利用列式计算即得.
【详解】数列的前n项和为,所以.故选:B
5.D【分析】根据赋值法求系数和得,即可根据展开式的通项公式求解.
【详解】令,得,得,
则的展开式的通项,
令,得r=3,则,故展开式中的系数为﹣945,故选:D.
6.D【分析】根据等比数列的定义解决问题.
【详解】由题意知,解得,
故.故选:D.
7.B【分析】根据分步计数原理分析求解即可.
【详解】甲有3种参加方法,乙有2种参加方法,丙、丁均有3种参加方法,根据分步乘法计数原理可知,甲、乙不在同一个植树小组的安排方法有3×2×3×3=54种,故选:B.
8.B【分析】利用全概率公式计算可得.
【详解】设A=“发送的信号为0”,B=“接收到的信号为0”,
则“发送的信号为1”,“接收到的信号为1”,
所以,
所以接收信号为1的概率为:,
解得p=0.85,故选:B.
9.C【分析】甲队得25分且取得该局比赛胜利包含甲以25:22取得比赛胜利和甲以25:23取得胜利两个事件,再利用事件的相互独立性及互斥事件加法公式求概率.
【详解】记事件A=“甲队得25分且取得该局比赛胜利”,
事件B=“甲以25:22取得该局胜利”,C=“甲以25:23取得该局胜利”,
因为各次发球的胜负结果相互独立,且B,C互斥,所以,
,
所以,
所以甲队得25分且取得该局比赛胜利的概率为.故选:C
10.D【分析】A选项,计算出,故不是等比数列,A错误;
B选项,计算出的前三项,得到,B错误;
C选项,由题干条件得到,故为等比数列,得到,
故,相加即可求出,C错误;
D选项,在的基础上,分奇偶项,分别得到通项公式,最后求出.
【详解】由题意得:,
由于,故数列不是等比数列,A错误;
则,
由于,故数列不为等比数列,B错误;
时,,即,
又,
故为等比数列,首项为2,公比为3,
故,
故,
以上20个式子相加得:,C错误;
因为,所以,两式相减得:
,
当时,
以上式子相加得:,
故,而也符和该式,故,
令得:,
当时,
以上式子相加得:,
故,而也符号该式,故,
令得:,综上:,D正确.故选:D
【点睛】当遇到时,数列往往要分奇数项和偶数项,分别求出通项公式,最后再检验能不能合并为一个,这类题目的处理思路可分别令和,用累加法进行求解.
11.17 【分析】将,时分别代入偶数与奇数对应通项,即可求解.
【详解】依题意,.故答案为:17
12.155 【分析】由等差数列求和公式即可得解.
【详解】由题意.故答案为:155.
13.0.5/
【分析】根据独立事件同时发生的概率公式,即可求解.
【详解】若两人都没有投进,概率,
若两人都投进,概率,
则得分相等的概率.故答案为:0.5
14. 【分析】第10行从左至右依次为,,,…,,由二项式系数性质可得答案.
【详解】观察知第10行从左至右依次为,,,…,,
由二项式系数的性质可得最大,其次为,
所以第10行中最大的数与第二大的数的数值之比为.故答案为:.
15.①③④
【分析】把题设中的数列分成如下的组:(1),(1,2),(1,2,4),(1,2,4,8),…,求出每组的和为,命题①通过计算每组项数的和求解;命题②恰好是前10组之和;命题③通过找到符合题意得出判断;命题④设前n项由前k行和第k+1行前,项组成,算出前n和为后结合前n项和为2的整数幂可得n的最小值.
【详解】将数列排成行的形式
1,
1,2,
1,2,4,
1,2,4,8,
…
第行为:,则第k行和为,
前k行共有个数,前k行的和为,
对于命题①,第10个1出现在第1+2+3+4+5+6+7+8+9+1=46项,故①正确;
对于命题②,因为,所以数列的前55项的和是,故②错误;
对于命题③,因为,是3的倍数,所以存在连续六项之和是3的倍数,故③正确;
对于命题④,设前n项由前k行和第k+1行前项组成,则.
前n项和为,若前n项和为2的整数幂,则有,即.
因为,所以当时,;
当时,;
当时,;
当时,;
所以满足前n项之和为2的整数幂,且n>100的最小整数n的值为440,故④正确.
故答案为:①③④
【点睛】关键点点睛:本题考查分组数列的和以及与不定方程的整数解,对于分组数列的前n项和的问题,一般采用计算“大组”和,再计算“小组”和,而不定方程的整数解问题,则需把和式放缩为2的正整数幂的形式,从而确定和的表达式.
16.(1);
(2)时取得最大值为36.
【分析】(1)根据已知及等差数列通项公式求基本量,进而写出通项公式;
(2)写出等差数列前n项和,应用其二次函数性质求最大值和对应n.
【详解】(1)设等差数列的公差为d,则,
故,所以.
(2)由,且,
所以,
故n=6时取得最大,最大值为36.
17.(1);(2).
【分析】(1)设等差数列的公差为d,根据题意列出关于和d的方程组求解即可;
(2)证明是等比数列,根据等比数列前n项和公式即可求解.
【详解】(1)设等差数列的公差为,
∵成等比数列,
解得
∴;
(2)由(1)得,,
∴,
∴是首项为4,公比为4的等比数列,
∴.
18.(1) (2) (3)
【分析】(1)由题意知总样本数为17,C:古建筑及历史纪念建筑物共有11,利用古典概型概率公式从而求解.
(2)由题意可知小王参观A:革命遗址及革命纪念建筑物与小张参观C:古建筑及历史纪念建筑物在同一个区的只有东城区,然后分别求出他们参观东城区的概率,从而求解.
(3)利用分类讨论求出抽到海淀区的概率和抽不到海淀区的概率,从而求解.
【详解】(1)设选中参观单位恰好为“C:古建筑及历史纪念建筑物”为事件C,
由题意知总共有17个,“C:古建筑及历史纪念建筑物”有11,所以.
(2)设两人选择的参观单位恰好在同一个区为事件B,由题意可知小王参观A:革命遗址及革命纪念建筑物与小张参观C:古建筑及历史纪念建筑物在同一个区的只有东城区,
所以小王参观东城区景区的概率为,小张参观东城区景区的概率为.
所以.
(3)当抽到的2个都是海淀区的概率为,
当抽到的2个中有1个是海淀区的概率为,
所以,所以.
19.(1)
(2)证明见解析
【分析】(1)由与的关系结合等比数列的定义、通项计算即可;
(2)利用等差数列求和公式结合裂项相消法证明不等式即可.
【详解】(1)由已知,
又,即是以3为首项和公比的等比数列,
即;
(2)由(1)可知,所以,
则,
因为,显然,则,证毕.
20.(1) (2)分布列见解析, (3)4.4
【分析】(1)记“该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨”为事件A,推出只有8月份的可回收物中废纸和塑料品的回收量均超过4.0吨,然后求解概率.
(2)X的所有可能取值为1,2,3,利用超几何概率公式求出概率得到分布列,然后求解期望即可.
(3)根据方差的计算公式,结合二次函数的性质即可求解最小值.
【详解】(1)记“该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨”为事件A由题意,只有8月份的可回收物中废纸和塑料品的回收量均超过4.0吨 所以
(2)因为回收利用1吨废纸可再造出0.8吨好纸
所以7月至12月回收的废纸可再造好纸超过3.0吨的月份有:7月、8月、10月,共3个月.
X的所有可能取值为1,2,3.
,,
所以X的分布列为:
X 0 1 2
P
(3),当添加的新数a等于原几个数的平均值时,方差最小.
理由如下:由于2020年6月至2020年12月该垃圾处理场可回收物中塑料品的回收量分别为2.8,3.5,4.9,4.2,4.9,4.9,5.6,故其平均数为
2020年6月至2021年1月该垃圾处理场可回收物中塑料品的回收量方差为
,
其中为2020年6月至2020年12月该垃圾处理场可回收物中塑料品的回收量)
由于为定值,所以只需要取最小即可,
根据二次函数的性质可知当取最小,所以当添加的新数a等于原几个数的平均值时,方差最小.
21.(1)(ⅰ);(ⅱ)证明见解析 (2)证明见解析
【分析】(1)(ⅰ)结合条件代入计算即可;
(ⅱ)若,由于2023﹣1=2022,所以当,数列为递增数列,不能存在降低的部分,否则达不到2023,若数列的公差为﹣1,;
(2)假设为数列的第一个为0项,而后进行反证即可.
【详解】(1)解:(ⅰ)因为,所以当,
数列为递增数列,且公差为1,不能存在降低的部分,
所以.
(ⅱ)若,由于2023﹣1=2022,
所以当,数列为递增数列,且公差为1,不能存在降低的部分,
否则达不到2023,所以其是充分条件,
若数列的公差为﹣1,,可见其是不必要条件,
所以“”是“为等差数列”的充分不必要条件;
(2)证明:假设,是数列第一个为0项,则,
所以或,以此类推,可得(p,q为整数),
显然与已知矛盾.所以数列不含等于零的项.
【点睛】与数列的新定义有关的问题的求解策略:
1、通过给出一个新的数列的定义,或约定一种新的运算,或给出几个新模型来创设新问题的情景,要求在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实心信息的迁移,达到灵活解题的目的;
2、遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使得问题得以解决.
同课章节目录
