北师大版2023-2024学年数学七年级下册期中测试试题(基础卷含解析)
文档属性
| 名称 | 北师大版2023-2024学年数学七年级下册期中测试试题(基础卷含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 21:54:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级下册期中测试试题(北师大版)基础卷含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)数据用科学记数法表示为( )
A. B. C. D.
2.(本题3分)下列计算正确的是( )
A. B.
C. D.
3.(本题3分)观察下列运算
我们发现规律:(为正整数):利用这个公式计算:( )
A.32022﹣1 B. C. D.
4.(本题3分)一副三角板按如图所示叠放在一起,若固定,将绕着公共顶点,按顺时针方向旋转,当的一边与的某一边平行时,相应的旋转角的值不可能是( )
A. B. C. D.
5.(本题3分)下列各图中,与是对顶角的是 ( )
A. B.
C. D.
6.(本题3分)如图,平移直线至,直线,被直线所截,,则的度数为( )
A. B. C. D.
7.(本题3分)建筑队在工地一边靠墙处,用81米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则关于的函数关系式为( )
A. B.
C. D.
8.(本题3分)炎炎夏日,冰激凌成为非常受欢迎的舌尖上的味道,某商店统计了一款冰激凌6月份前6天每天的供应量和销售量,结果如下表:
1日 2日 3日 4日 5日 6日
供应量(个) 90 100 90 100 90 100
销售量(个) 80 90 85 80 90 85
记为6月t日冰激凌的供应量,为6月t日冰激凌的销售量,其中,2,…,30.用销售指数(,)来评价从6月t日开始连续n天的冰激凌的销售情况.
当时,表示6月t日的日销售指数.给出下列四个结论:
①在6月1日至6日的日销售指数中,最小,最大;
②在6月1日至6日这6天中,日销售指数越大,说明该天冰激凌的销售量越大;
③;
④如果6月7日至12日冰激凌每天的供应量和销售量分别与6月1日至6日每天的供应量和销售量对应相等,则对任意,2,3,4,5,6,7,都有
其中所有正确结论的序号是( ).
A.①② B.②③ C.①④ D.①③④
9.(本题3分)某校八年级(4)班用150元购买了某品牌乒乓球个,该品牌乒乓球的单价是元/个,其函数关系式为,在这个问题中,变量是( )
A.150,x B.150,y C.x,y D.,
10.(本题3分)已知均为常数,均为非零常数,若有两个整式,,下列结论中,正确个数为( )
①当为关于的三次三项式时,则;
②当多项式乘积不含时,则;
③;
④当能被整除时,;
⑤若或时,无论和取何值,值总相等,则.
A.4 B.3 C.2 D.1
评卷人得分
二、填空题(共24分)
11.(本题3分)计算: .
12.(本题3分)若的展开式中不含x的一次项,则a的值为 .
13.(本题3分)若与的两边分别平行,且比的2倍少,则的度数为 .
14.(本题3分)数学兴趣小组同学利用几何图形画出螳螂的简笔画,如图,已知,且,则 .
15.(本题3分)如图,两直线交于点O,若,则 .
16.(本题3分)如图是一个数据转换器的示意图,则与的关系式是 .
17.(本题3分)表格中列出了一个试验的统计数据,表示皮球从高处落下时,弹跳高度与下降高度的关系.给出下列关系式:①;②;③;④.其中能表示这种关系的是 .(填序号)
18.(本题3分)若,则 .
评卷人得分
三、解答题(共66分)
19.(本题8分)计算:
20.(本题8分)先化简,再求值∶,其中.
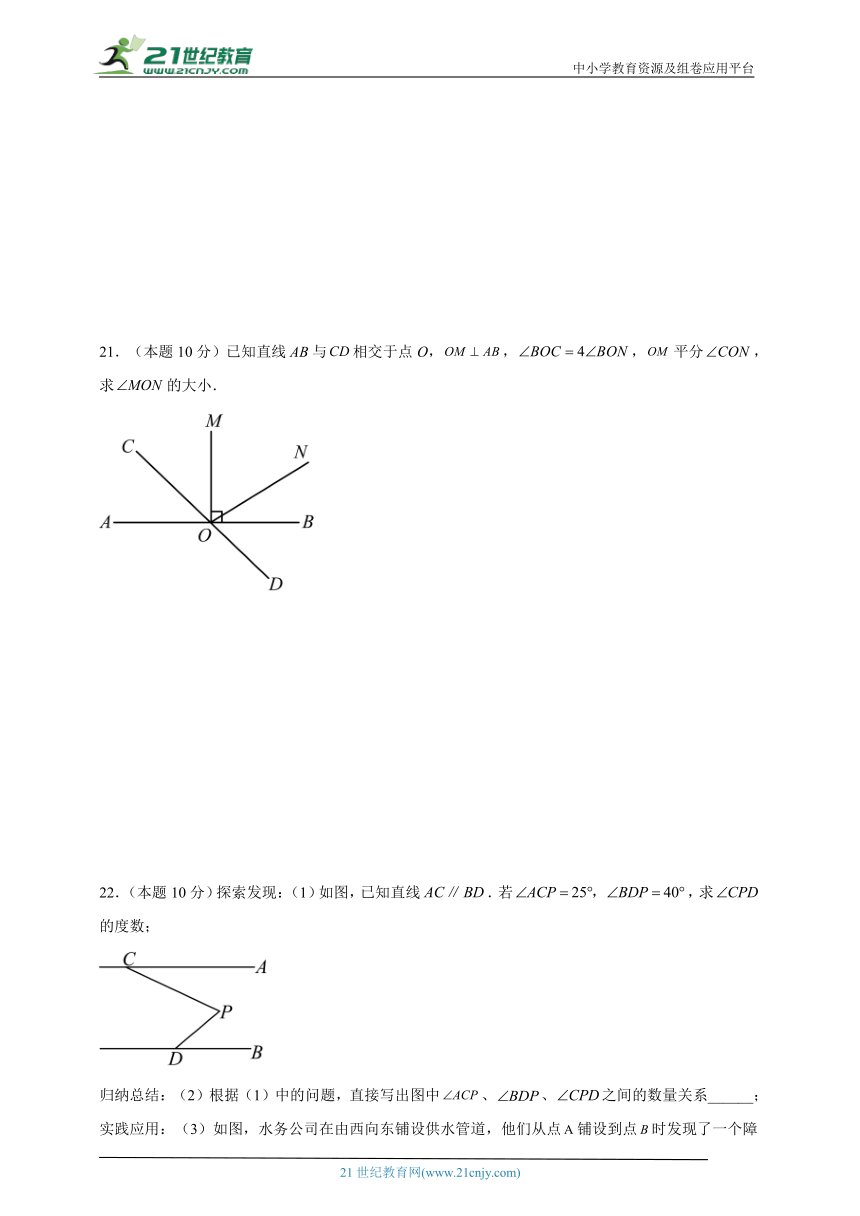
21.(本题10分)已知直线与相交于点O,,,平分,求的大小.
22.(本题10分)探索发现:(1)如图,已知直线.若,求的度数;
归纳总结:(2)根据(1)中的问题,直接写出图中、、之间的数量关系______;
实践应用:(3)如图,水务公司在由西向东铺设供水管道,他们从点铺设到点时发现了一个障碍物,不得不改变方向绕开障碍物,计划改为沿南偏东方向埋设到点,再沿障碍物边缘埋设到点处,测得.若要恢复原来的正东方向,则应等于多少度?
23.(本题10分)填写下表,并观察表中两个代数式的值的变化情况.
a 1 2 3 4 5 6 7 8 …
…
…
(1)随着a的值逐渐增大,两个代数式的值有什么变化?
(2)估计哪个代数式的值先达到;
(3)在表左端的代数式中,哪些量是变量?哪些量是常量?
24.(本题10分)科学家认为二氧化碳的释放量越来越多是全球变暖的原因之一.下表年全世界所释放的二氧化碳量:
年份 1950 1960 1970 1980 1990
释放量百万吨 6002 9475 14989 19287 22588
(1)上表反映的是哪两个变量之间的关系?
(2)说一说这两个变量之间的关系.
25.(本题10分)一辆汽车油箱内有油升,从某地出发,每行驶千米,耗油升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化
(1)写出与的关系式______.
(2)这辆汽车行驶千米时剩油多少升?汽车剩油升时,行驶了多少千米?
参考答案:
1.C
【分析】此题考查科学记数法的表示方法,科学记数法的表示形式为的形式,其中,为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数,当原数绝对值时,是负整数.
【详解】解:数据用科学记数法表示为.
故选:C.
2.A
【分析】本题考查幂的乘方、积的乘方、单项式除以单项式以及完全平方公式,根据运算法则逐一判定即可.
【详解】解:,故A正确;
,故B错误,不符合题意;
,故C错误,不符合题意;
,故D错误,不符合题意;
故选:A.
3.D
【分析】本题考查了多项式乘法中的规律性问题.
根据运算规律,代入,,整理后即可求解.
【详解】解:∵,
当,时,,
∴,
故选:.
4.B
【分析】本题考查平行线的判定与性质,要分类讨论,不要漏掉一种情况,也可实际用三角板操作找到它们之间的关系;再计算.
【详解】由题意可得旋转角
分5种情况讨论:
(1)当时,,则
此时;
(2)当时,,则
(3)当时,,则
此时;
(4)当时,,
(5)当时,,则
此时;
∴相应的旋转角的值不可能是,
故选:B.
5.C
【分析】此题主要考查学生对顶角概念,掌握“有公共顶点且两条边都互为反向延长线的两个角互为对顶角”是解题的关键.
【详解】A.两条边没有互为反向延长线,故错误;
B.两条边没有互为反向延长线,故错误;
C.有公共顶点且两条边都互为反向延长线,故正确;
D.两条边没有互为反向延长线,故错误;
故选C.
6.C
【分析】本题考查了平移的性质,平行线的性质,对顶角相等,根据平移可得,根据平行线的性质以及对顶角相等,即可求解.
【详解】解:如图所示,
∵平移直线至
∴
∴
又∵,
∴
故选:C.
7.D
【分析】本题主要考查了列函数关系式,根据题意先求出平行于墙的一边长为米,再根据长方形面积计算公式求解即可.
【详解】解:由题意得,平行于墙的一边长为米,
∴,
故选:D.
8.C
【分析】根据题意,,最大,,最小,故①正确;6月2日销售指数小于6月5日,但是两天的销售量却相等,故②错误;;,,故③错误;
根据题意,,,∵,
∴,
对任意,2,3,4,5,6,7,都有正确,解答即可.本题考查了函数模型的选择和应用,正确理解题意是解题的关键.
【详解】根据题意,,最大,,最小,
故①正确;
6月2日销售指数小于6月5日,但是两天的销售量却相等,
故②错误;
;,
,
故③错误;
根据题意,,,∵,
∴,
对任意,2,3,4,5,6,7,都有正确,
故选:C.
9.C
【分析】本题是关于函数的基础题.根据题目中的数量关系与自变量、因变量的定义即可求解.
【详解】解:函数关系式为,在这个问题中,变量是x,y.
故选:C.
10.B
【分析】
本题考查了整式的加减运算与乘法运算,求出,可得当时,为关于的三次三项式,此时,故说法①错误;求出,再由多项式乘积不含,可得,解得:,故说法②错误;当时,可得,当时,可得,故③说法正确;设,可得,令得到,,故④说法正确;根据当或时,无论和取何值,A值总相等,可得且,故⑤说法正确,即可.
【详解】解:∵,,
∴,
当时,为关于的三次三项式,此时,故说法①错误;
∵多项式乘积不含,
∴,解得:,故说法②错误;
∵,
当时,,
即,
当时,,
即,
∴,故③说法正确;
∵A能被整除,
∴可设,
∵
∴,
令得:,即
∴,故④说法正确;
当时,,
当时,,
∵当或时,无论和取何值,A值总相等,
∴且,
解得:,故⑤说法正确;
正确的有:③④⑤,共3个.
故选:B.
11.
【分析】本题考查了完全平方公式,解题关键是熟练掌握完全平方公式,根据完全平方公式运算即可.
【详解】解:,
故答案为:.
12.
【分析】本题考查多项式乘多项式,根据多项式乘多项式法则展开,令x的一次项系数为0即可.
【详解】解:,
∵的展开式中不含x的一次项,
∴,
∴,
故答案为:.
13.或
【分析】根据平行线的性质可得或,再根据题意可得,再代入求解即可.
【详解】解:∵与的两边分别平行,
∴或,
∵比的2倍少,
∴,
∴或,
故答案为:或.
14./18度
【分析】本题考查了平行线的判定与性质,过点C作,先证明,然后根据平行线的性质求出,最后利用角的和差关系求解即可.
【详解】过点C作,则
∵,
∴,
∴,
又∵,
∴,
∴.
故答案为:.
15./38度
【分析】本题考查对顶角的性质,解题关键是掌握对顶角相等的性质.
根据对顶角的性质求解.
【详解】解:∵与互为对顶角,
∴
故答案为:.
16.
【分析】本题考查的知识点是用关系式表示变量间的关系,解题关键是理解题意.
根据示意图的流程逐步进行即可求得与的关系式.
【详解】解:根据数据转换器的示意图流程即可求得与的关系式:
输入——,
减去——,
平方——,
加上——,
输出结果——,
即.
故答案为:.
17.②
【分析】
本题考查求函数关系式,根据表格即可得到,关系即可得到答案;
【详解】解:由表格可得,
∵,,,,
∴,
故答案为:②.
18.
【分析】本题考查了完全平方公式应用,设,,则,,由完全平方公式即可求解,掌握完全平方公式是解题的关键.
【详解】解:设,,
∴,,
∴,
∴,
∴,
故答案为:.
19.
【分析】本题考查的是多项式除以单项式,直接按照多项式除以单项式的法则计算即可.
【详解】解:
;
20.,
【分析】本题主要考查运用乘法公式进行整式运算,代入求值,掌握整式运算法则是解题的关键.
根据乘法公式展开,再根据整式混合运算法则进行计算,最后代入求值即可.
【详解】解:
,
当,时,原式.
21.
【分析】本题考查了垂直的定义,角平分线的概念,角的和差运算等知识;设,则,从而得;由角平分线的条件得;利用垂直关系和为90度建立方程即可求解.
【详解】解:∵,设,则,
∴,
∵OM平分,
∴,
∵,
∴,
∵,
∴,
解得,
∴.
22.(1);(2);(3)应等于
【分析】本题考查了平行线判定与性质,平行线性质求角度,熟练掌握平行线的判定与性质是解题关键.
(1)过点P作,根据两直线平行内错角相等可得,根据进行求解即可;
(2)根据两直线平行内错角相等即可推到出;
(3)过点C作,先求出的度数,再根据两直线平行同旁内角互补求解即可.
【详解】解:(1)如图,过点P作,
,
,
,
;
(2)由(1)可得:;
(3)如图,过点C作,
,
,
,
,
,
,
,
,
,
若要恢复原来的正东方向,则应等于.
23.(1)随着a的值逐渐增大,两个代数式的值也随着增大
(2)
(3)在中,自变量为a,常量为5和6;在中,自变量为a,常量为2
【分析】本题考查了变量和常量.熟练掌握在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量是解题的关键.
(1)通过计算填表格,然后依据表格中的数值变化进行作答即可;
(2)依据表格中的数值变化进行作答即可;
(3)根据变量、常量的定义进行作答即可.
【详解】(1)解:由题意,填表格如下:
a 1 2 3 4 5 6 7 8 …
…
1 4 9 …
由表格可知,随着a的值逐渐增大,两个代数式的值也随着增大;
(2)解:由表格可知,的增加速度更快,
∴估计先达到;
(3)解:由题意知,在中,自变量为a,常量为5和6;在中,自变量为a,常量为2.
24.(1)释放量与年份;(2)释放量的随着年份的增加而增大
【分析】(1)分别根据变量、因变量的定义分别得出即可;
(2)根据图表分析得出答案.
【详解】解:(1)上标反映的是释放量与年份之间的关系;
(2)释放量的随着年份的增加而增大.
【点睛】本题考查了常量与变量的定义以及利用图表得出正确方案等知识,利用图表获取正确数据是解题关键.
25.(1)
(2)升;千米
【分析】
本题考查变量间的关系,根据题意得变量之间得关系式是解决问题的关键.
(1)根据总油量减去用油量等于剩余油量,可得变量之间的关系式;
(2)根据自变量,可得相应的因变量的值,根据因变量的值,可得相应自变量的值.
【详解】(1)y与的关系式是,
故答案为:;
(2)
当时,,
所以汽车行驶千米时剩油升;
当时,,
解得:,
所以汽车行驶千米时剩油升.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级下册期中测试试题(北师大版)基础卷含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)数据用科学记数法表示为( )
A. B. C. D.
2.(本题3分)下列计算正确的是( )
A. B.
C. D.
3.(本题3分)观察下列运算
我们发现规律:(为正整数):利用这个公式计算:( )
A.32022﹣1 B. C. D.
4.(本题3分)一副三角板按如图所示叠放在一起,若固定,将绕着公共顶点,按顺时针方向旋转,当的一边与的某一边平行时,相应的旋转角的值不可能是( )
A. B. C. D.
5.(本题3分)下列各图中,与是对顶角的是 ( )
A. B.
C. D.
6.(本题3分)如图,平移直线至,直线,被直线所截,,则的度数为( )
A. B. C. D.
7.(本题3分)建筑队在工地一边靠墙处,用81米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则关于的函数关系式为( )
A. B.
C. D.
8.(本题3分)炎炎夏日,冰激凌成为非常受欢迎的舌尖上的味道,某商店统计了一款冰激凌6月份前6天每天的供应量和销售量,结果如下表:
1日 2日 3日 4日 5日 6日
供应量(个) 90 100 90 100 90 100
销售量(个) 80 90 85 80 90 85
记为6月t日冰激凌的供应量,为6月t日冰激凌的销售量,其中,2,…,30.用销售指数(,)来评价从6月t日开始连续n天的冰激凌的销售情况.
当时,表示6月t日的日销售指数.给出下列四个结论:
①在6月1日至6日的日销售指数中,最小,最大;
②在6月1日至6日这6天中,日销售指数越大,说明该天冰激凌的销售量越大;
③;
④如果6月7日至12日冰激凌每天的供应量和销售量分别与6月1日至6日每天的供应量和销售量对应相等,则对任意,2,3,4,5,6,7,都有
其中所有正确结论的序号是( ).
A.①② B.②③ C.①④ D.①③④
9.(本题3分)某校八年级(4)班用150元购买了某品牌乒乓球个,该品牌乒乓球的单价是元/个,其函数关系式为,在这个问题中,变量是( )
A.150,x B.150,y C.x,y D.,
10.(本题3分)已知均为常数,均为非零常数,若有两个整式,,下列结论中,正确个数为( )
①当为关于的三次三项式时,则;
②当多项式乘积不含时,则;
③;
④当能被整除时,;
⑤若或时,无论和取何值,值总相等,则.
A.4 B.3 C.2 D.1
评卷人得分
二、填空题(共24分)
11.(本题3分)计算: .
12.(本题3分)若的展开式中不含x的一次项,则a的值为 .
13.(本题3分)若与的两边分别平行,且比的2倍少,则的度数为 .
14.(本题3分)数学兴趣小组同学利用几何图形画出螳螂的简笔画,如图,已知,且,则 .
15.(本题3分)如图,两直线交于点O,若,则 .
16.(本题3分)如图是一个数据转换器的示意图,则与的关系式是 .
17.(本题3分)表格中列出了一个试验的统计数据,表示皮球从高处落下时,弹跳高度与下降高度的关系.给出下列关系式:①;②;③;④.其中能表示这种关系的是 .(填序号)
18.(本题3分)若,则 .
评卷人得分
三、解答题(共66分)
19.(本题8分)计算:
20.(本题8分)先化简,再求值∶,其中.
21.(本题10分)已知直线与相交于点O,,,平分,求的大小.
22.(本题10分)探索发现:(1)如图,已知直线.若,求的度数;
归纳总结:(2)根据(1)中的问题,直接写出图中、、之间的数量关系______;
实践应用:(3)如图,水务公司在由西向东铺设供水管道,他们从点铺设到点时发现了一个障碍物,不得不改变方向绕开障碍物,计划改为沿南偏东方向埋设到点,再沿障碍物边缘埋设到点处,测得.若要恢复原来的正东方向,则应等于多少度?
23.(本题10分)填写下表,并观察表中两个代数式的值的变化情况.
a 1 2 3 4 5 6 7 8 …
…
…
(1)随着a的值逐渐增大,两个代数式的值有什么变化?
(2)估计哪个代数式的值先达到;
(3)在表左端的代数式中,哪些量是变量?哪些量是常量?
24.(本题10分)科学家认为二氧化碳的释放量越来越多是全球变暖的原因之一.下表年全世界所释放的二氧化碳量:
年份 1950 1960 1970 1980 1990
释放量百万吨 6002 9475 14989 19287 22588
(1)上表反映的是哪两个变量之间的关系?
(2)说一说这两个变量之间的关系.
25.(本题10分)一辆汽车油箱内有油升,从某地出发,每行驶千米,耗油升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化
(1)写出与的关系式______.
(2)这辆汽车行驶千米时剩油多少升?汽车剩油升时,行驶了多少千米?
参考答案:
1.C
【分析】此题考查科学记数法的表示方法,科学记数法的表示形式为的形式,其中,为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数,当原数绝对值时,是负整数.
【详解】解:数据用科学记数法表示为.
故选:C.
2.A
【分析】本题考查幂的乘方、积的乘方、单项式除以单项式以及完全平方公式,根据运算法则逐一判定即可.
【详解】解:,故A正确;
,故B错误,不符合题意;
,故C错误,不符合题意;
,故D错误,不符合题意;
故选:A.
3.D
【分析】本题考查了多项式乘法中的规律性问题.
根据运算规律,代入,,整理后即可求解.
【详解】解:∵,
当,时,,
∴,
故选:.
4.B
【分析】本题考查平行线的判定与性质,要分类讨论,不要漏掉一种情况,也可实际用三角板操作找到它们之间的关系;再计算.
【详解】由题意可得旋转角
分5种情况讨论:
(1)当时,,则
此时;
(2)当时,,则
(3)当时,,则
此时;
(4)当时,,
(5)当时,,则
此时;
∴相应的旋转角的值不可能是,
故选:B.
5.C
【分析】此题主要考查学生对顶角概念,掌握“有公共顶点且两条边都互为反向延长线的两个角互为对顶角”是解题的关键.
【详解】A.两条边没有互为反向延长线,故错误;
B.两条边没有互为反向延长线,故错误;
C.有公共顶点且两条边都互为反向延长线,故正确;
D.两条边没有互为反向延长线,故错误;
故选C.
6.C
【分析】本题考查了平移的性质,平行线的性质,对顶角相等,根据平移可得,根据平行线的性质以及对顶角相等,即可求解.
【详解】解:如图所示,
∵平移直线至
∴
∴
又∵,
∴
故选:C.
7.D
【分析】本题主要考查了列函数关系式,根据题意先求出平行于墙的一边长为米,再根据长方形面积计算公式求解即可.
【详解】解:由题意得,平行于墙的一边长为米,
∴,
故选:D.
8.C
【分析】根据题意,,最大,,最小,故①正确;6月2日销售指数小于6月5日,但是两天的销售量却相等,故②错误;;,,故③错误;
根据题意,,,∵,
∴,
对任意,2,3,4,5,6,7,都有正确,解答即可.本题考查了函数模型的选择和应用,正确理解题意是解题的关键.
【详解】根据题意,,最大,,最小,
故①正确;
6月2日销售指数小于6月5日,但是两天的销售量却相等,
故②错误;
;,
,
故③错误;
根据题意,,,∵,
∴,
对任意,2,3,4,5,6,7,都有正确,
故选:C.
9.C
【分析】本题是关于函数的基础题.根据题目中的数量关系与自变量、因变量的定义即可求解.
【详解】解:函数关系式为,在这个问题中,变量是x,y.
故选:C.
10.B
【分析】
本题考查了整式的加减运算与乘法运算,求出,可得当时,为关于的三次三项式,此时,故说法①错误;求出,再由多项式乘积不含,可得,解得:,故说法②错误;当时,可得,当时,可得,故③说法正确;设,可得,令得到,,故④说法正确;根据当或时,无论和取何值,A值总相等,可得且,故⑤说法正确,即可.
【详解】解:∵,,
∴,
当时,为关于的三次三项式,此时,故说法①错误;
∵多项式乘积不含,
∴,解得:,故说法②错误;
∵,
当时,,
即,
当时,,
即,
∴,故③说法正确;
∵A能被整除,
∴可设,
∵
∴,
令得:,即
∴,故④说法正确;
当时,,
当时,,
∵当或时,无论和取何值,A值总相等,
∴且,
解得:,故⑤说法正确;
正确的有:③④⑤,共3个.
故选:B.
11.
【分析】本题考查了完全平方公式,解题关键是熟练掌握完全平方公式,根据完全平方公式运算即可.
【详解】解:,
故答案为:.
12.
【分析】本题考查多项式乘多项式,根据多项式乘多项式法则展开,令x的一次项系数为0即可.
【详解】解:,
∵的展开式中不含x的一次项,
∴,
∴,
故答案为:.
13.或
【分析】根据平行线的性质可得或,再根据题意可得,再代入求解即可.
【详解】解:∵与的两边分别平行,
∴或,
∵比的2倍少,
∴,
∴或,
故答案为:或.
14./18度
【分析】本题考查了平行线的判定与性质,过点C作,先证明,然后根据平行线的性质求出,最后利用角的和差关系求解即可.
【详解】过点C作,则
∵,
∴,
∴,
又∵,
∴,
∴.
故答案为:.
15./38度
【分析】本题考查对顶角的性质,解题关键是掌握对顶角相等的性质.
根据对顶角的性质求解.
【详解】解:∵与互为对顶角,
∴
故答案为:.
16.
【分析】本题考查的知识点是用关系式表示变量间的关系,解题关键是理解题意.
根据示意图的流程逐步进行即可求得与的关系式.
【详解】解:根据数据转换器的示意图流程即可求得与的关系式:
输入——,
减去——,
平方——,
加上——,
输出结果——,
即.
故答案为:.
17.②
【分析】
本题考查求函数关系式,根据表格即可得到,关系即可得到答案;
【详解】解:由表格可得,
∵,,,,
∴,
故答案为:②.
18.
【分析】本题考查了完全平方公式应用,设,,则,,由完全平方公式即可求解,掌握完全平方公式是解题的关键.
【详解】解:设,,
∴,,
∴,
∴,
∴,
故答案为:.
19.
【分析】本题考查的是多项式除以单项式,直接按照多项式除以单项式的法则计算即可.
【详解】解:
;
20.,
【分析】本题主要考查运用乘法公式进行整式运算,代入求值,掌握整式运算法则是解题的关键.
根据乘法公式展开,再根据整式混合运算法则进行计算,最后代入求值即可.
【详解】解:
,
当,时,原式.
21.
【分析】本题考查了垂直的定义,角平分线的概念,角的和差运算等知识;设,则,从而得;由角平分线的条件得;利用垂直关系和为90度建立方程即可求解.
【详解】解:∵,设,则,
∴,
∵OM平分,
∴,
∵,
∴,
∵,
∴,
解得,
∴.
22.(1);(2);(3)应等于
【分析】本题考查了平行线判定与性质,平行线性质求角度,熟练掌握平行线的判定与性质是解题关键.
(1)过点P作,根据两直线平行内错角相等可得,根据进行求解即可;
(2)根据两直线平行内错角相等即可推到出;
(3)过点C作,先求出的度数,再根据两直线平行同旁内角互补求解即可.
【详解】解:(1)如图,过点P作,
,
,
,
;
(2)由(1)可得:;
(3)如图,过点C作,
,
,
,
,
,
,
,
,
,
若要恢复原来的正东方向,则应等于.
23.(1)随着a的值逐渐增大,两个代数式的值也随着增大
(2)
(3)在中,自变量为a,常量为5和6;在中,自变量为a,常量为2
【分析】本题考查了变量和常量.熟练掌握在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量是解题的关键.
(1)通过计算填表格,然后依据表格中的数值变化进行作答即可;
(2)依据表格中的数值变化进行作答即可;
(3)根据变量、常量的定义进行作答即可.
【详解】(1)解:由题意,填表格如下:
a 1 2 3 4 5 6 7 8 …
…
1 4 9 …
由表格可知,随着a的值逐渐增大,两个代数式的值也随着增大;
(2)解:由表格可知,的增加速度更快,
∴估计先达到;
(3)解:由题意知,在中,自变量为a,常量为5和6;在中,自变量为a,常量为2.
24.(1)释放量与年份;(2)释放量的随着年份的增加而增大
【分析】(1)分别根据变量、因变量的定义分别得出即可;
(2)根据图表分析得出答案.
【详解】解:(1)上标反映的是释放量与年份之间的关系;
(2)释放量的随着年份的增加而增大.
【点睛】本题考查了常量与变量的定义以及利用图表得出正确方案等知识,利用图表获取正确数据是解题关键.
25.(1)
(2)升;千米
【分析】
本题考查变量间的关系,根据题意得变量之间得关系式是解决问题的关键.
(1)根据总油量减去用油量等于剩余油量,可得变量之间的关系式;
(2)根据自变量,可得相应的因变量的值,根据因变量的值,可得相应自变量的值.
【详解】(1)y与的关系式是,
故答案为:;
(2)
当时,,
所以汽车行驶千米时剩油升;
当时,,
解得:,
所以汽车行驶千米时剩油升.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
