1.3.2奇偶性
图片预览






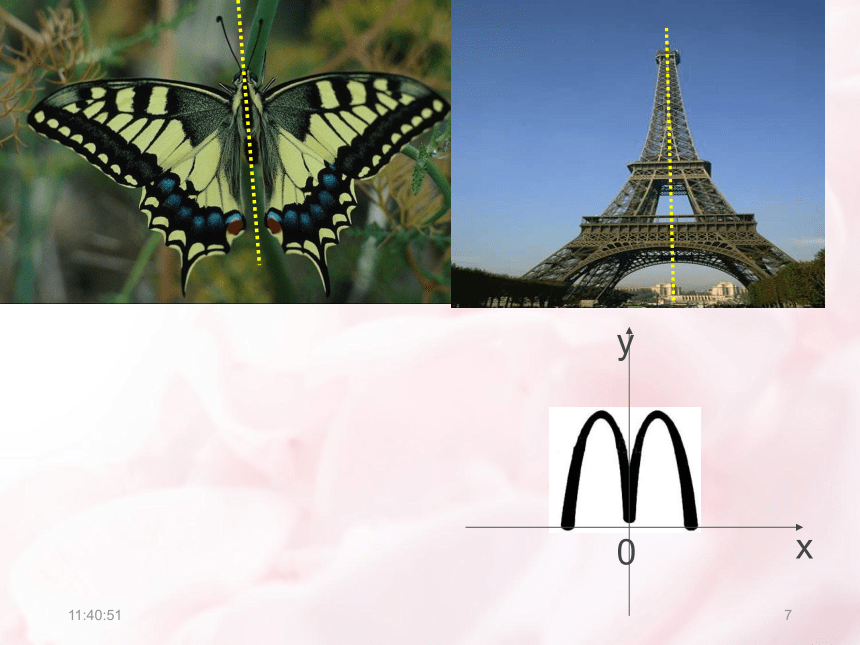



文档简介
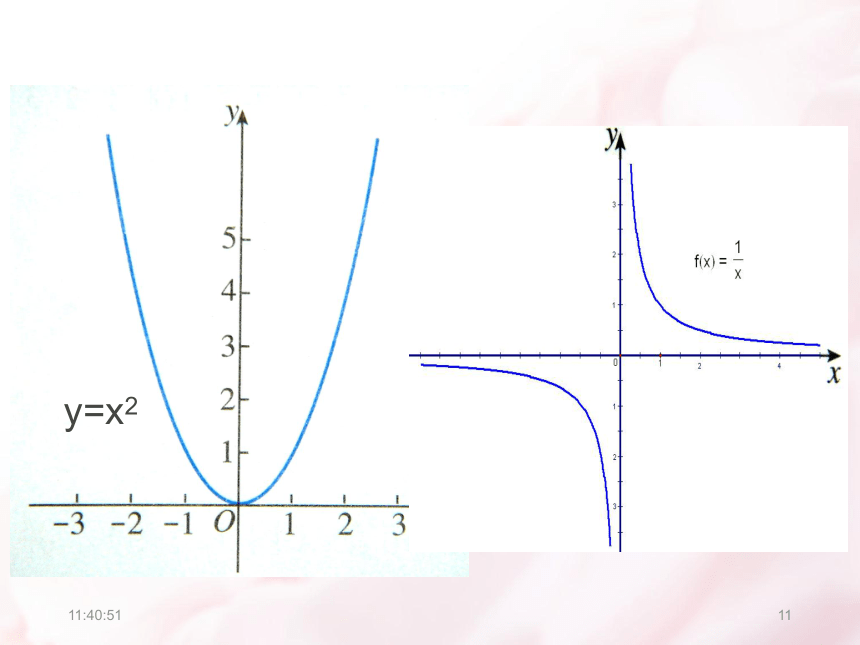
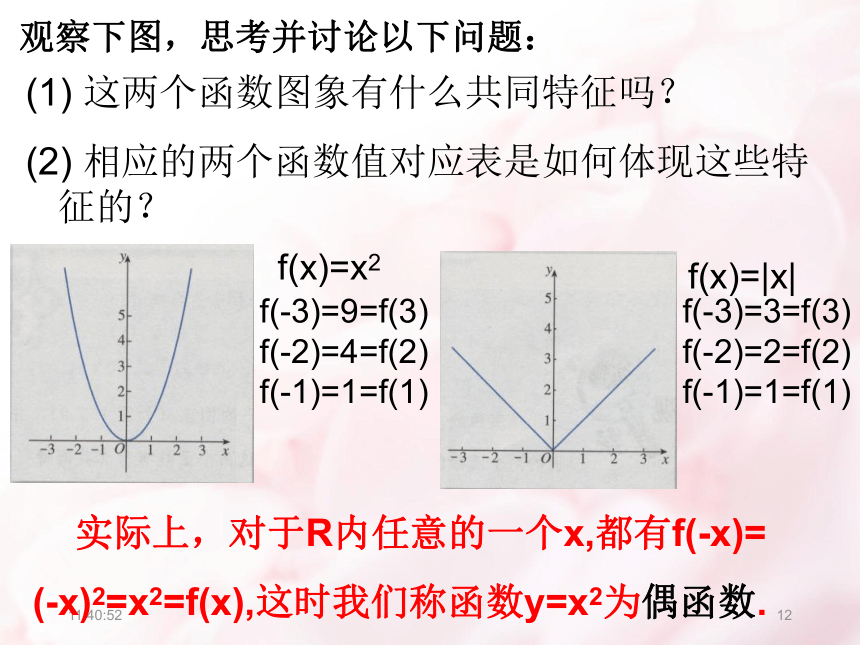
课件39张PPT。21:11:0111.3.2 奇偶性21:11:012观察下列图片,你有何感受?21:11:01321:11:01421:11:01521:11:01621:11:01721:11:01821:11:01921:11:011021:11:0111y=x221:11:0112观察下图,思考并讨论以下问题:(1) 这两个函数图象有什么共同特征吗?
(2) 相应的两个函数值对应表是如何体现这些特征的?f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1) 实际上,对于R内任意的一个x,都有f(-x)=
(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.21:11:0113偶函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. 例如,函数 都是偶函数,它们的图象分别如下图(1)、(2)所示.21:11:0114小结:偶函数的图象关于y轴对称。 如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数(evenfuntion)。21:11:0115C全优基础夯实(一)21:11:0116 观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1) 实际上,对于R内任意的一个x,都有f(-x)=-x
=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)21:11:0117 如果对于函数f(x)的定义域内的任意一个x,都有f(-x)= -f(x),那么函数f(x)就叫做奇函数(oddfuntion)。小结:奇函数的图象关于原点对称。21:11:01183.设奇函数f(x)的定义域为[-5,5],当x∈[0,5]时,函数y=f(x)的图象如图所示,则使函数值y<0的x的取值集合为_______________.(-2,0)∪(2,5)全优变式训练(一)21:11:0119注意: 1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;2、由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).21:11:01200-1全优限时规范训练(一)[-1,1]全优基础夯实(二)21:11:0121函数的奇偶性概念:
对于函数f(x),在它的定义域内,把任
意一个x换成-x,(x,-x都在定义域)。
①如果都有f(-x)=f(x),则函数f(x)叫
做偶函数。
②如果都有f(-x)=-f(x),则函数f(x)叫
做奇函数。21:11:0122例5、判断下列函数的奇偶性:(1)解:定义域为R
f(-x)=(-x)4=x4=f(x)即f(-x)=f(x)∴f(x)偶函数(2)解:定义域为R f(-x)=(-x)5=- x5 =-f(x)即f(-x)=-f(x)∴f(x)奇函数(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)即f(-x)=-f(x)∴f(x)奇函数(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)即f(-x)=f(x)∴f(x)偶函数21:11:0123练习:课本36页1(1)(3)【例1】 判断下列函数的奇偶性:解:(3)函数f(x)的定义域是(-∞,-1)∪(-1,+∞).
不关于原点对称,
∴f(x)是非奇非偶函数.全优典例剖析(一)21:11:0124【例1】 判断下列函数的奇偶性:(2)f(x)=|x+1|+|x-1|解:(2)f(x)的定义域是R,
又f(-x)=|-x+1|+|-x-1|
=|x-1|+|x+1|=f(x),
∴f(x)是偶函数.全优典例剖析(一)21:11:01251.判断下列函数的奇偶性:解:(2)f(x)定义域为{x|x≠0},关于原点对称,故f(x)为偶函数.全优变式训练(一)全优能力提升(一)21:11:0127奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.21:11:0128解:函数f(x)的定义域是R,关于原点对称,
当x<0时,-x>0,
f(-x)=-x-1=-(x+1)=-f(x);
当x>0时,-x<0,
f(-x)=-x+1=-(x-1)=-f(x),
而f(0)=0,∴f(x)是奇函数.全优变式训练(一)21:11:0129思考:是否存在函数f(x)既是奇函数又是偶函数?若存在,这样的函数有何特征?一个函数就奇偶性而言有哪几种可能情形?例:判断下列函数的奇偶性21:11:0130函数按是否有奇偶性可分为四类:奇函数
偶函数
既是奇函数又是偶函数
既不是奇函数又不是偶函数 既是奇函数又是偶函数的函数是函数值为0的常值函数. 前提是定义域关于原点对称.21:11:01311.下列说法错误的个数为( )
①图像关于原点对称的函数是奇函数;
②图像关于y轴对称的函数是偶函数;
③奇函数的图象一定过原点;
④偶函数的图象一定与y轴相交。
A.4 B.3 C.2 D.0CD全优限时规范训练(一)全优基础夯实(二)21:11:0132若函数f(x)为奇函数,且在x=0处有定义,则f(0)的值能确定吗?由奇函数的定义知f(-0)=-f(0),
即f(0)=-f(0),
∴f(0)=0.
021:11:0133-2全优能力提高(一)21:11:01340,0全优能力提高(二)21:11:0135 第一步先判断函数的定义域是否关于原点对称;
第二步判断f (-x)=f (x)还是判断f (-x)=-f (x).归 纳: 根据定义判断一个函数是奇函数还是偶函数的方法和步骤是:21:11:0136全优35页要点阐述2(2)21:11:0137【例1】 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=-2x2+3x+1.
(1)求f(0)的值; (2)当x<0时,求f(x)的解析式;
(3)求f(x)在R上的解析式.解:(1)因为函数f(x)是定义在R上的奇函数,
所以f(-0)=-f(0),即f(0)=0.
(2)当x<0时,-x>0,
f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.
由于f(x)是奇函数,故f(x)=-f(-x),
所以f(x)=2x2+3x-1,x<0.全优典例剖析(二)21:11:0138【例1】 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=-2x2+3x+1.
(1)求f(0)的值; (2)当x<0时,求f(x)的解析式;
(3)求f(x)在R上的解析式.21:11:0139-2x2+4全优限时规范训练(二)
(2) 相应的两个函数值对应表是如何体现这些特征的?f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1) 实际上,对于R内任意的一个x,都有f(-x)=
(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.21:11:0113偶函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. 例如,函数 都是偶函数,它们的图象分别如下图(1)、(2)所示.21:11:0114小结:偶函数的图象关于y轴对称。 如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数(evenfuntion)。21:11:0115C全优基础夯实(一)21:11:0116 观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1) 实际上,对于R内任意的一个x,都有f(-x)=-x
=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)21:11:0117 如果对于函数f(x)的定义域内的任意一个x,都有f(-x)= -f(x),那么函数f(x)就叫做奇函数(oddfuntion)。小结:奇函数的图象关于原点对称。21:11:01183.设奇函数f(x)的定义域为[-5,5],当x∈[0,5]时,函数y=f(x)的图象如图所示,则使函数值y<0的x的取值集合为_______________.(-2,0)∪(2,5)全优变式训练(一)21:11:0119注意: 1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;2、由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).21:11:01200-1全优限时规范训练(一)[-1,1]全优基础夯实(二)21:11:0121函数的奇偶性概念:
对于函数f(x),在它的定义域内,把任
意一个x换成-x,(x,-x都在定义域)。
①如果都有f(-x)=f(x),则函数f(x)叫
做偶函数。
②如果都有f(-x)=-f(x),则函数f(x)叫
做奇函数。21:11:0122例5、判断下列函数的奇偶性:(1)解:定义域为R
f(-x)=(-x)4=x4=f(x)即f(-x)=f(x)∴f(x)偶函数(2)解:定义域为R f(-x)=(-x)5=- x5 =-f(x)即f(-x)=-f(x)∴f(x)奇函数(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)即f(-x)=-f(x)∴f(x)奇函数(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)即f(-x)=f(x)∴f(x)偶函数21:11:0123练习:课本36页1(1)(3)【例1】 判断下列函数的奇偶性:解:(3)函数f(x)的定义域是(-∞,-1)∪(-1,+∞).
不关于原点对称,
∴f(x)是非奇非偶函数.全优典例剖析(一)21:11:0124【例1】 判断下列函数的奇偶性:(2)f(x)=|x+1|+|x-1|解:(2)f(x)的定义域是R,
又f(-x)=|-x+1|+|-x-1|
=|x-1|+|x+1|=f(x),
∴f(x)是偶函数.全优典例剖析(一)21:11:01251.判断下列函数的奇偶性:解:(2)f(x)定义域为{x|x≠0},关于原点对称,故f(x)为偶函数.全优变式训练(一)全优能力提升(一)21:11:0127奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.21:11:0128解:函数f(x)的定义域是R,关于原点对称,
当x<0时,-x>0,
f(-x)=-x-1=-(x+1)=-f(x);
当x>0时,-x<0,
f(-x)=-x+1=-(x-1)=-f(x),
而f(0)=0,∴f(x)是奇函数.全优变式训练(一)21:11:0129思考:是否存在函数f(x)既是奇函数又是偶函数?若存在,这样的函数有何特征?一个函数就奇偶性而言有哪几种可能情形?例:判断下列函数的奇偶性21:11:0130函数按是否有奇偶性可分为四类:奇函数
偶函数
既是奇函数又是偶函数
既不是奇函数又不是偶函数 既是奇函数又是偶函数的函数是函数值为0的常值函数. 前提是定义域关于原点对称.21:11:01311.下列说法错误的个数为( )
①图像关于原点对称的函数是奇函数;
②图像关于y轴对称的函数是偶函数;
③奇函数的图象一定过原点;
④偶函数的图象一定与y轴相交。
A.4 B.3 C.2 D.0CD全优限时规范训练(一)全优基础夯实(二)21:11:0132若函数f(x)为奇函数,且在x=0处有定义,则f(0)的值能确定吗?由奇函数的定义知f(-0)=-f(0),
即f(0)=-f(0),
∴f(0)=0.
021:11:0133-2全优能力提高(一)21:11:01340,0全优能力提高(二)21:11:0135 第一步先判断函数的定义域是否关于原点对称;
第二步判断f (-x)=f (x)还是判断f (-x)=-f (x).归 纳: 根据定义判断一个函数是奇函数还是偶函数的方法和步骤是:21:11:0136全优35页要点阐述2(2)21:11:0137【例1】 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=-2x2+3x+1.
(1)求f(0)的值; (2)当x<0时,求f(x)的解析式;
(3)求f(x)在R上的解析式.解:(1)因为函数f(x)是定义在R上的奇函数,
所以f(-0)=-f(0),即f(0)=0.
(2)当x<0时,-x>0,
f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.
由于f(x)是奇函数,故f(x)=-f(-x),
所以f(x)=2x2+3x-1,x<0.全优典例剖析(二)21:11:0138【例1】 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=-2x2+3x+1.
(1)求f(0)的值; (2)当x<0时,求f(x)的解析式;
(3)求f(x)在R上的解析式.21:11:0139-2x2+4全优限时规范训练(二)
