9.1.2不等式的性质(广东省湛江市霞山区20中)
文档属性
| 名称 | 9.1.2不等式的性质(广东省湛江市霞山区20中) |  | |
| 格式 | rar | ||
| 文件大小 | 328.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-09 13:55:00 | ||
图片预览







文档简介
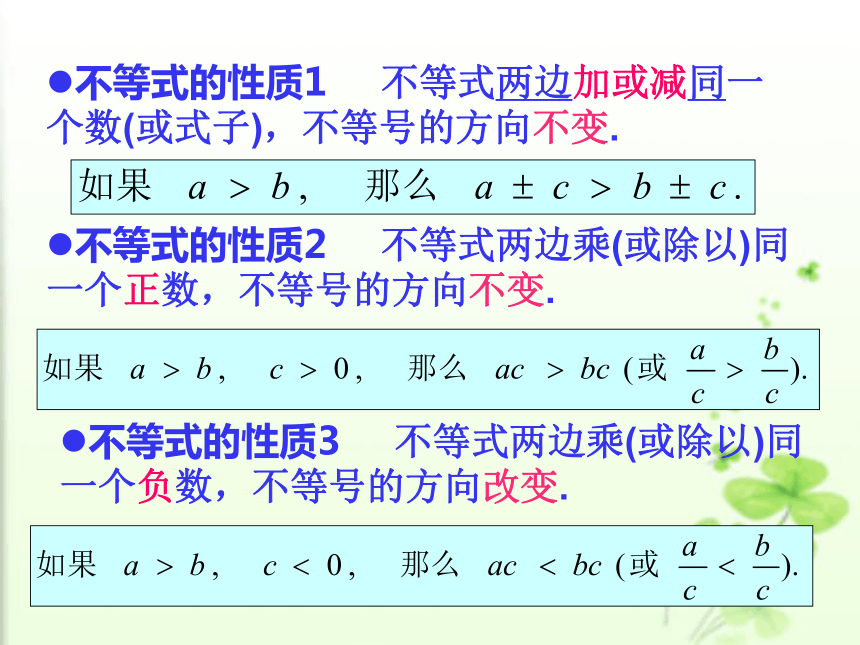
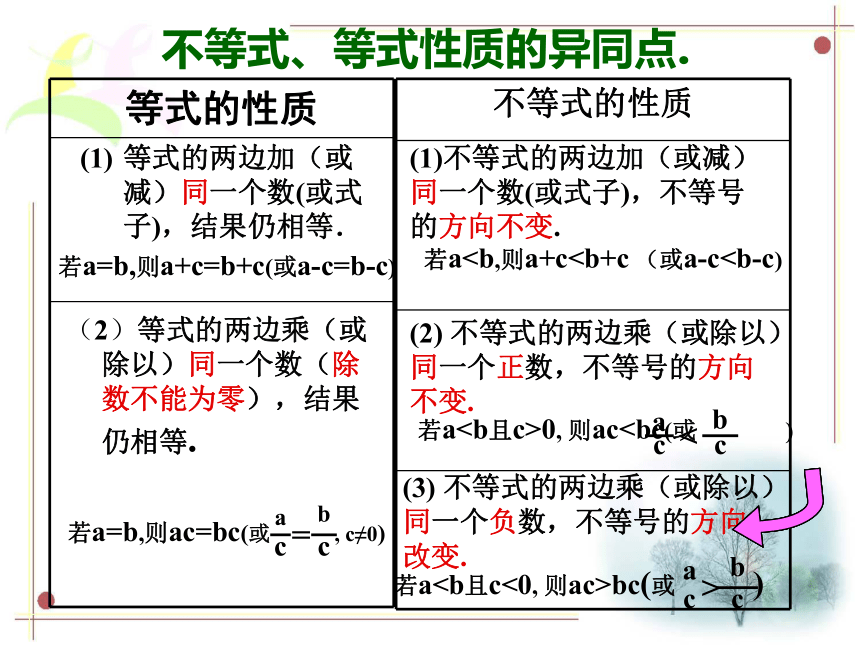
课件21张PPT。不等式的性质授课人:沈海尉(1)什么叫不等式?粉红色的回忆 用不等号(“<” “>” “≠” “≥” “≤” )表示不等关系的式子叫不等式. (2)什么叫一元一次不等式? 含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式。等式两边乘或除以同一个数(除数不为0),结果仍相等.等式两边加或减同一个数(或式子),结果仍相等.(4)等式的性质1(5)等式的性质2(3)什么叫不等式的解集 含有一个未知数的不等式的所有的解,叫做这个不等式的解集。等式的性质2 等式两边乘或除以同一个数(除数不为0),结果仍相等.等式的性质1 等式两边加或减同一个数(或式子),结果仍相等.⑴ -2+4____6+4
⑵ -2-4____6-4
⑶ -2×4____6×4
⑷ -2÷(-4)____6÷(-4)
>>><<用“>”或“<”填空 不等式(1)-(4)分别由不等式“7>4”做了怎样的变形?结果不等号的方向不变还是改变? 再来试一试! -2 <6<<>用“>”或“<”填空,并总结其中的规律。<>>><<不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式的性质1<><<>不等式的两边乘(或除以)同一个正数,不等号的方向不变.不等式的两边乘(或除以)同一个负数,不等号的方向改变.>不等式的性质2不等式的性质3用“>”或“<”填空,并总结其中的规律。从刚刚接触的这些不等式中,你能看出一些什么规律吗?不等式的性质1 不等式两边加或减同一个数(或式子),不等号的方向不变.不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变.若a0, 则ac 用“>”或“<”号填空
(1)已知a>b,则3a____3b;
(2)已知a>b,则-a____-b;
(3)已知a>b,则-a+2____-b+2.解:(1)因为a>b,根据不等式性质2,
两边同时乘以3得 3a>3b.(2)因为a>b,根据不等式性质3,
两边同时乘以-1得 -a<-b.聪明的你做对了吗?做一做>>><<判断:
(1)∵a (2) ∵a (3) ∵ a (4) ∵ -2a>0 ∴a>0
(5) ∵-a<-3 ∴a<3√√×××填空:
(1)∵ 2a> 3a ∴a是 数
(2)∵ a/2> a/3 ∴a是 数
(3) ∵ax1 ∴a是 数
负正负设m>n,用 “<“或 “>”填空
(1)m-5_____n-5 (2)m+4_____n+4
(3)6m_____6n (4)-2m_____-2n>>><设a>b,用 “< “或”>”填空
(1)2a-5______2b-5
(2)-3.5b+1_______-3.5a+1>>设a>b,用<或>填空(1)a-3 b-3;
(2)a÷3 b÷3
(3)0.1a 0.1b;
(4) -4a -4b
(5) 2a+3 2b+3;
(6) (m2+1) a (m2+1)b (m为常数)
>>><>>(8)若ac2>bc2,则a>b( )(7) 若a>b,则ac2>bc2( )×√根据下列已知条件,说出a与b的不等关系,并说明是根据不等式哪一个性质:知识应用判断对错并说明理由1. 因为-3<0,所以-3+1<1 ( ) 2. 因为-3 × 2> -5 ×2,所以-3<-5 ( )7. 因为-2<1,所以-2a < a ( )3. 若ab,则-a<- b ( )6. 若-2x>0,则x>0 ( )8. 若a>0,则3a>2a ( )√√√√××××已知a<-1,则下列不等式中错误的是( )
A.4a<-4 B.-4a<-4 C.a+2<1 D.2-a>3B已知x(1)x-3(3)-3x+2<-3y+2 (4)-3x+2>-3y+2 如果a>b,c>d,那么ac>bd.这句话正确吗?为什么?<>想一想5、由xmy的条件是 ( )
A . m≥0 B . m≤0 C. m>0 D. m<0
6、若mx1,则应为 ( )
A. m<0 B. m>0 C. m≤0 D. m≥0
7、若m是有理数,则-7m与3m的大小关系应是 ( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定DAD看谁做得快
⑵ -2-4____6-4
⑶ -2×4____6×4
⑷ -2÷(-4)____6÷(-4)
>>><<用“>”或“<”填空 不等式(1)-(4)分别由不等式“7>4”做了怎样的变形?结果不等号的方向不变还是改变? 再来试一试! -2 <6<<>用“>”或“<”填空,并总结其中的规律。<>>><<不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式的性质1<><<>不等式的两边乘(或除以)同一个正数,不等号的方向不变.不等式的两边乘(或除以)同一个负数,不等号的方向改变.>不等式的性质2不等式的性质3用“>”或“<”填空,并总结其中的规律。从刚刚接触的这些不等式中,你能看出一些什么规律吗?不等式的性质1 不等式两边加或减同一个数(或式子),不等号的方向不变.不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变.若a
(1)已知a>b,则3a____3b;
(2)已知a>b,则-a____-b;
(3)已知a>b,则-a+2____-b+2.解:(1)因为a>b,根据不等式性质2,
两边同时乘以3得 3a>3b.(2)因为a>b,根据不等式性质3,
两边同时乘以-1得 -a<-b.聪明的你做对了吗?做一做>>><<判断:
(1)∵a (2) ∵a (3) ∵ a (4) ∵ -2a>0 ∴a>0
(5) ∵-a<-3 ∴a<3√√×××填空:
(1)∵ 2a> 3a ∴a是 数
(2)∵ a/2> a/3 ∴a是 数
(3) ∵ax
负正负设m>n,用 “<“或 “>”填空
(1)m-5_____n-5 (2)m+4_____n+4
(3)6m_____6n (4)-2m_____-2n>>><设a>b,用 “< “或”>”填空
(1)2a-5______2b-5
(2)-3.5b+1_______-3.5a+1>>设a>b,用<或>填空(1)a-3 b-3;
(2)a÷3 b÷3
(3)0.1a 0.1b;
(4) -4a -4b
(5) 2a+3 2b+3;
(6) (m2+1) a (m2+1)b (m为常数)
>>><>>(8)若ac2>bc2,则a>b( )(7) 若a>b,则ac2>bc2( )×√根据下列已知条件,说出a与b的不等关系,并说明是根据不等式哪一个性质:知识应用判断对错并说明理由1. 因为-3<0,所以-3+1<1 ( ) 2. 因为-3 × 2> -5 ×2,所以-3<-5 ( )7. 因为-2<1,所以-2a < a ( )3. 若a
A.4a<-4 B.-4a<-4 C.a+2<1 D.2-a>3B已知x
A . m≥0 B . m≤0 C. m>0 D. m<0
6、若mx
A. m<0 B. m>0 C. m≤0 D. m≥0
7、若m是有理数,则-7m与3m的大小关系应是 ( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定DAD看谁做得快
