2.5.3切线长定理课件
图片预览


文档简介
课件17张PPT。切线长定理邵阳市第十五中学
彭雯
2018年11月29日9时9分温故知新1、圆的切线________过切点的半径
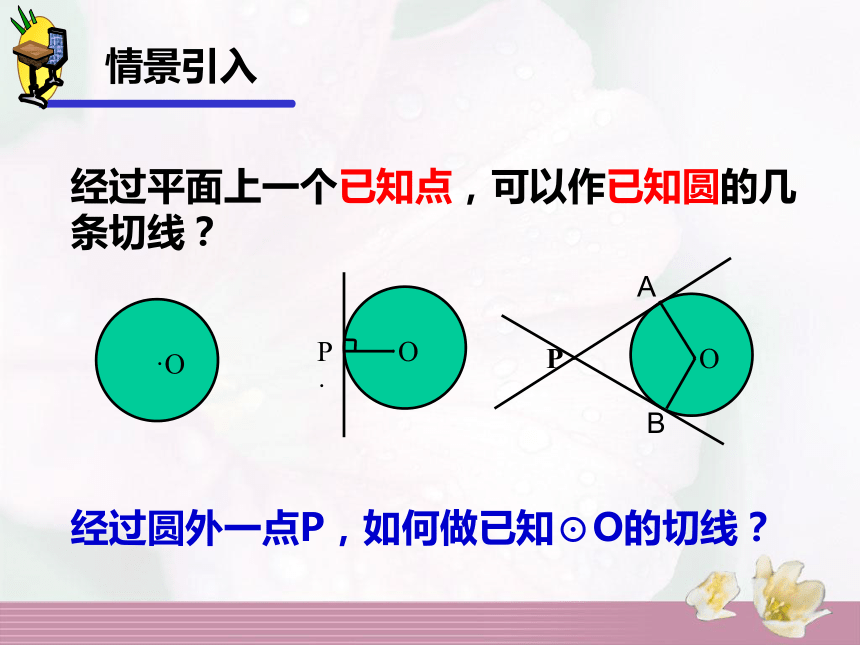
2、经过半径______并且_______这条半径的直是圆的切线垂直于外端垂直于情景引入经过平面上一个已知点,可以作已知圆的几条切线?P ·P ·AB经过圆外一点P,如何做已知⊙O的切线? 1、如何过⊙O外一点P画出⊙O的切线?
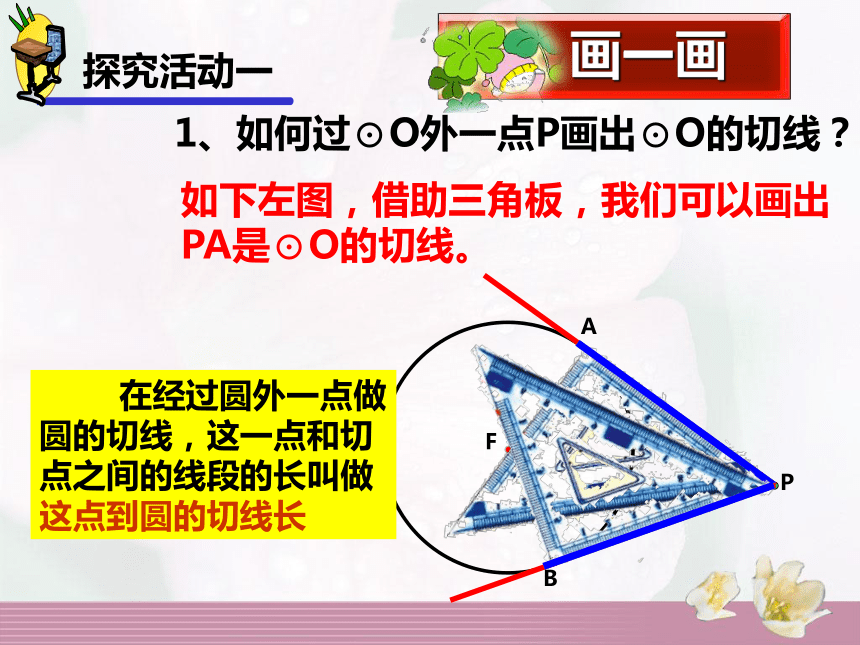
如下左图,借助三角板,我们可以画出PA是⊙O的切线。画一画 在经过圆外一点做圆的切线,这一点和切点之间的线段的长叫做这点到圆的切线长FAPB探究活动一
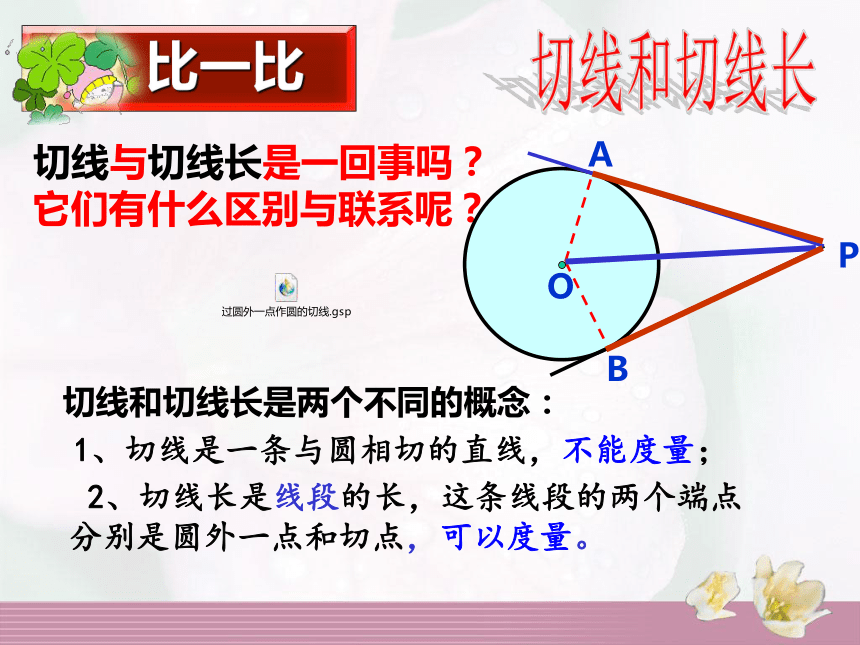
切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。切线和切线长比一比切线与切线长是一回事吗?它们有什么区别与联系呢?
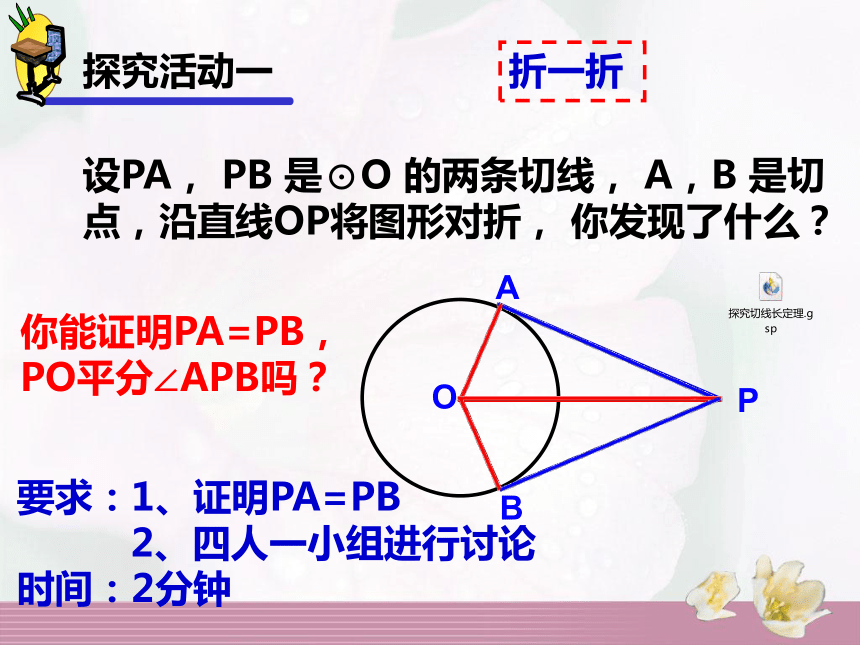
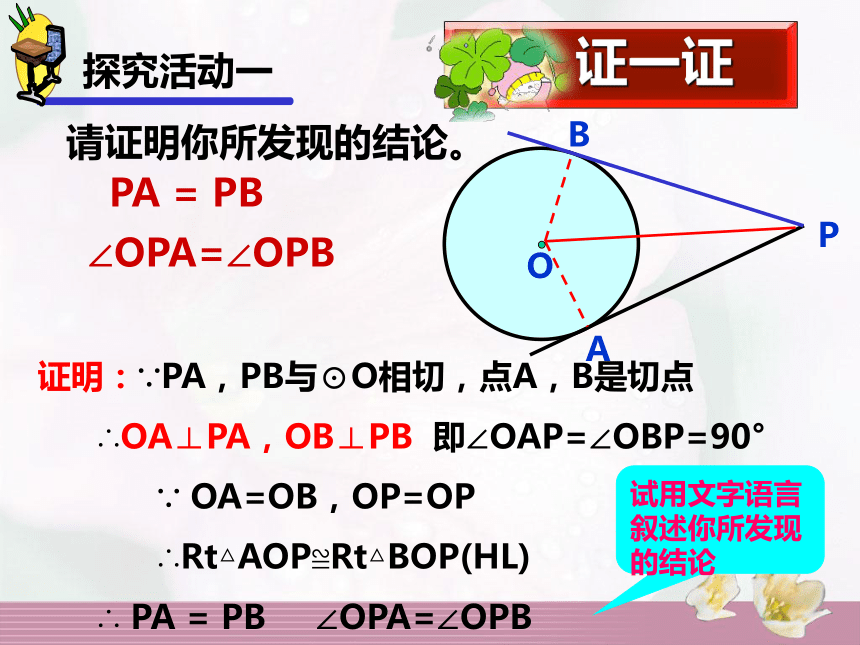
探究活动一折一折设PA, PB 是⊙O 的两条切线, A,B 是切点,沿直线OP将图形对折, 你发现了什么?POBA你能证明PA=PB,PO平分∠APB吗?要求:1、证明PA=PB
2、四人一小组进行讨论
时间:2分钟请证明你所发现的结论。PA = PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB试用文字语言叙述你所发现的结论
证一证探究活动一探究活动一结论过圆外一点所画的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.几何语言:∵PA、PB分别切⊙O 于A、B∴PA = PB,∠OPA=∠OPBAPOB1.若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB探究活动二 若PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
BAPOCED(3)写出图中所有的垂直关系OA⊥PA,OB ⊥PB,AB ⊥OP(5)写出图中所有的全等三角形△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP(4)写出图中所有的等腰三角形△ABP △AOB(1)写出图中所有相等的线段AO=BO=DO=EO,AP=BP,AC=BC(2)写出图中所有相等的弧AD=BD,AE=BE,DAE=DBE定理拓展探究活动二探究活动二如图,AD是⊙O的直径,点C为⊙O外一点,CA和CB是⊙O的切线,A和B是切点,连接BD.求证: CO∥BD.证明:连接AB.
∵ CA,CB是⊙O的切线,点A,B为切点,
∴ CA = CB, ∠ACO =∠BCO.
∴ CO⊥AB.
∵ AD是⊙O的直径,
∴ ∠ABD= 90°,
即 BD⊥AB.
∴ CO∥BD.拓展应用1.(珠海·中考)如图,PA,PB是⊙ O的切线,
切点分别是A,B,如果∠P=60°,那么∠AOB等
于( ) A.60° B.90°
C.120° D.150°C做一做一、判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。 (1)如图PA、PB切圆于A、B两点, 连结PO,则 度。PBOA二、填空25判断对错 如图,已知半圆O与四边形ABCD的边AD,AB, BC相切,切点分别为D,E,C. 设半圆O的半径为2,AB为5,求四边形ABCD的周长.试一试解 ∵ AD、AE 分别与⊙O 相切,
∴ AD=AE.
同理,BE=BC.
∴ 四边形 ABCD 的周长
=AD+AE+EB+BC+DC
=2AB+DC
=2×5+2×2
=14. 1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPB切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。BAP课堂小结已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=12cm,求△PEF的周长.【解析】易证EQ=EA, FQ=FB,PA=PB.∴ PE+EQ=PA=12cm,PF+FQ=PB=PA=12cm.∴周长为24cm.F布置作业
1、必做P75A组5
2、选做P76B组11
彭雯
2018年11月29日9时9分温故知新1、圆的切线________过切点的半径
2、经过半径______并且_______这条半径的直是圆的切线垂直于外端垂直于情景引入经过平面上一个已知点,可以作已知圆的几条切线?P ·P ·AB经过圆外一点P,如何做已知⊙O的切线? 1、如何过⊙O外一点P画出⊙O的切线?
如下左图,借助三角板,我们可以画出PA是⊙O的切线。画一画 在经过圆外一点做圆的切线,这一点和切点之间的线段的长叫做这点到圆的切线长FAPB探究活动一
切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。切线和切线长比一比切线与切线长是一回事吗?它们有什么区别与联系呢?
探究活动一折一折设PA, PB 是⊙O 的两条切线, A,B 是切点,沿直线OP将图形对折, 你发现了什么?POBA你能证明PA=PB,PO平分∠APB吗?要求:1、证明PA=PB
2、四人一小组进行讨论
时间:2分钟请证明你所发现的结论。PA = PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB试用文字语言叙述你所发现的结论
证一证探究活动一探究活动一结论过圆外一点所画的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.几何语言:∵PA、PB分别切⊙O 于A、B∴PA = PB,∠OPA=∠OPBAPOB1.若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB探究活动二 若PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
BAPOCED(3)写出图中所有的垂直关系OA⊥PA,OB ⊥PB,AB ⊥OP(5)写出图中所有的全等三角形△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP(4)写出图中所有的等腰三角形△ABP △AOB(1)写出图中所有相等的线段AO=BO=DO=EO,AP=BP,AC=BC(2)写出图中所有相等的弧AD=BD,AE=BE,DAE=DBE定理拓展探究活动二探究活动二如图,AD是⊙O的直径,点C为⊙O外一点,CA和CB是⊙O的切线,A和B是切点,连接BD.求证: CO∥BD.证明:连接AB.
∵ CA,CB是⊙O的切线,点A,B为切点,
∴ CA = CB, ∠ACO =∠BCO.
∴ CO⊥AB.
∵ AD是⊙O的直径,
∴ ∠ABD= 90°,
即 BD⊥AB.
∴ CO∥BD.拓展应用1.(珠海·中考)如图,PA,PB是⊙ O的切线,
切点分别是A,B,如果∠P=60°,那么∠AOB等
于( ) A.60° B.90°
C.120° D.150°C做一做一、判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。 (1)如图PA、PB切圆于A、B两点, 连结PO,则 度。PBOA二、填空25判断对错 如图,已知半圆O与四边形ABCD的边AD,AB, BC相切,切点分别为D,E,C. 设半圆O的半径为2,AB为5,求四边形ABCD的周长.试一试解 ∵ AD、AE 分别与⊙O 相切,
∴ AD=AE.
同理,BE=BC.
∴ 四边形 ABCD 的周长
=AD+AE+EB+BC+DC
=2AB+DC
=2×5+2×2
=14. 1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPB切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。BAP课堂小结已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=12cm,求△PEF的周长.【解析】易证EQ=EA, FQ=FB,PA=PB.∴ PE+EQ=PA=12cm,PF+FQ=PB=PA=12cm.∴周长为24cm.F布置作业
1、必做P75A组5
2、选做P76B组11
