人教版六年级下册数学4.2正比例和反比例(课件)(共30张PPT)
文档属性
| 名称 | 人教版六年级下册数学4.2正比例和反比例(课件)(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览






文档简介
(共30张PPT)
20XX
第四单元
比例
人教版数学六年级下册
正比例
正比例和反比例
一、复习导入
已知路程和时间,怎样求速度?
速度=路程÷时间
已知总价和数量,怎样求单价?
单价=总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率=工作总量÷工作时间
这节课我们一起来研究有特殊关系的两种相关联的量。
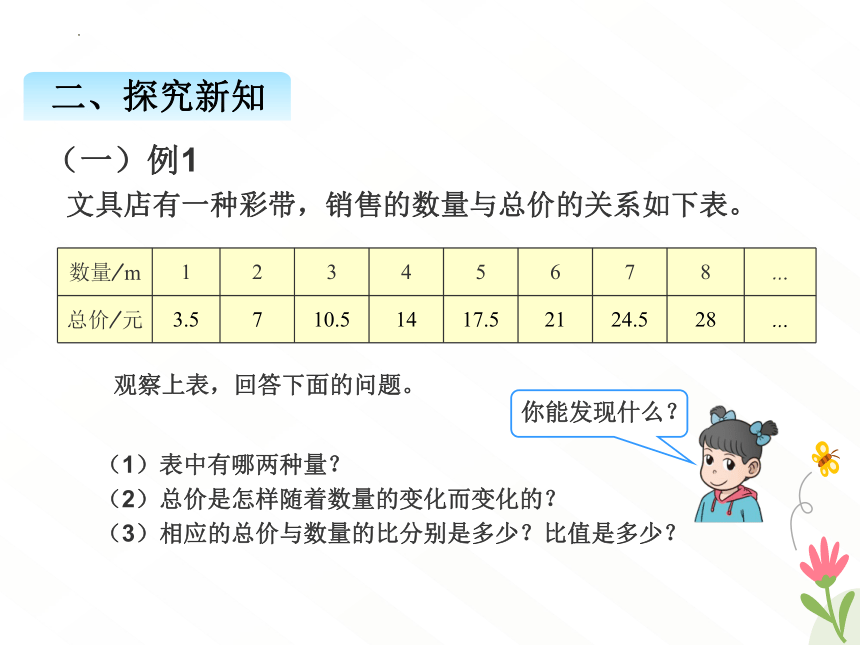
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)总价是怎样随着数量的变化而变化的?
(3)相应的总价与数量的比分别是多少?比值是多少?
你能发现什么?
二、探究新知
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
从上表可以看出,总价与数量是两种相关联的量,总价随着数量的变化而变化的,而且总价与相应数量的比值总是一定的。
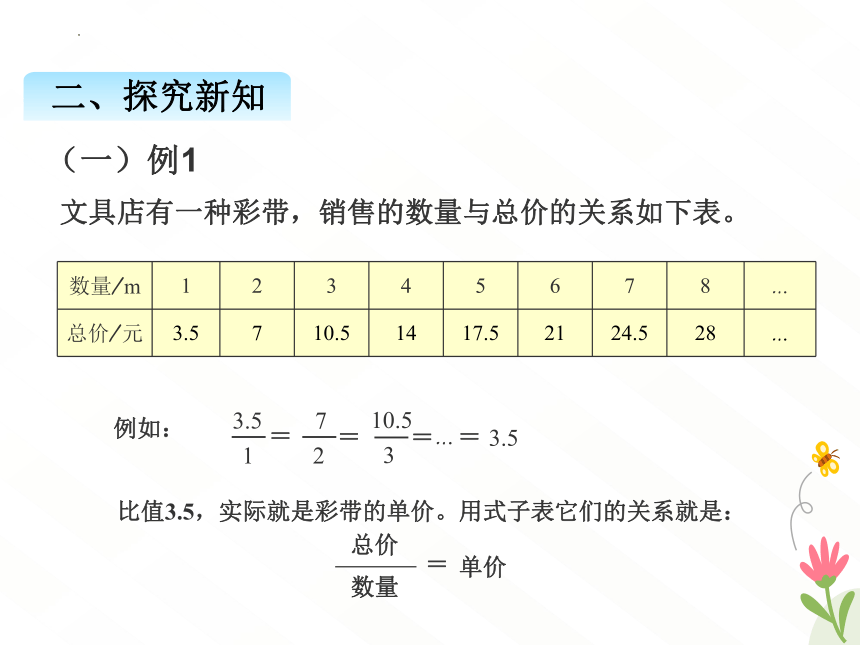
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
二、探究新知
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
单价
…
2
7
例如:
=
=
3.5
1
3.5
3
10.5
=
=
比值3.5,实际就是彩带的单价。用式子表它们的关系就是:
总价
数量
=
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
二、探究新知
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
总价
=
单价
数量
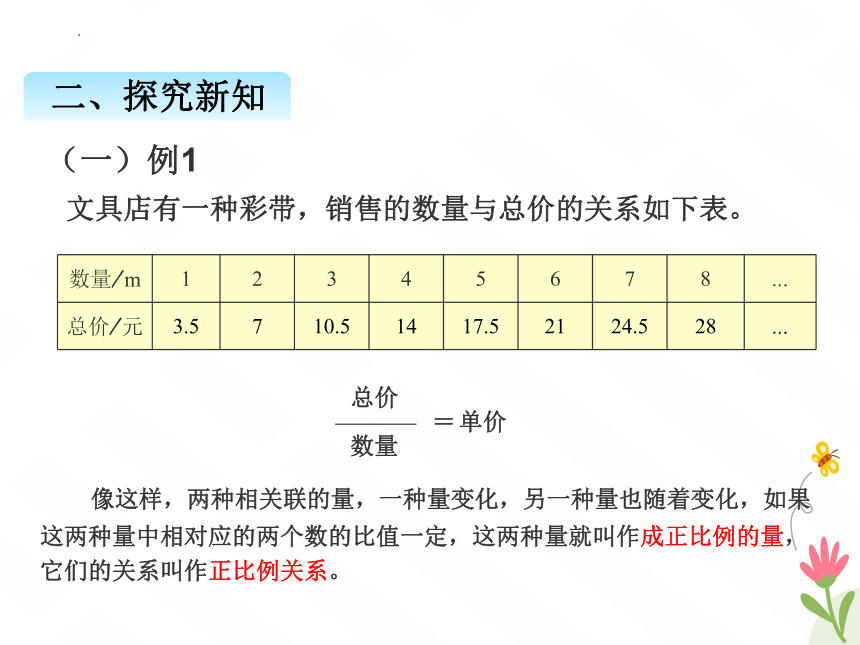
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
二、探究新知
上表中,总价和数量是成正比例的量,总价与数量成正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
总价
=
单价
数量
文具店有一种彩带,销售的数量与总价的关系如下表。
x
y
= k
(一)例1
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
二、探究新知
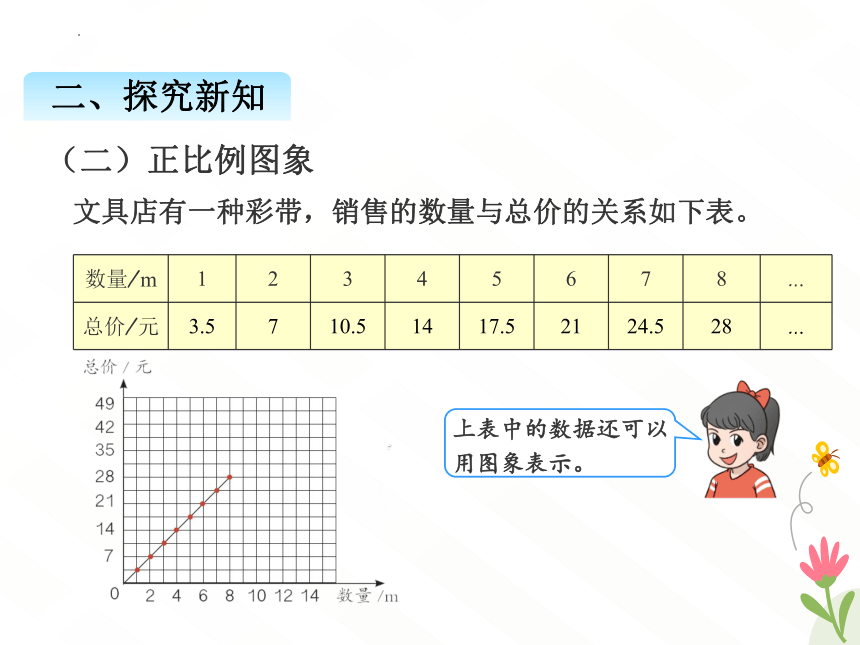
文具店有一种彩带,销售的数量与总价的关系如下表。
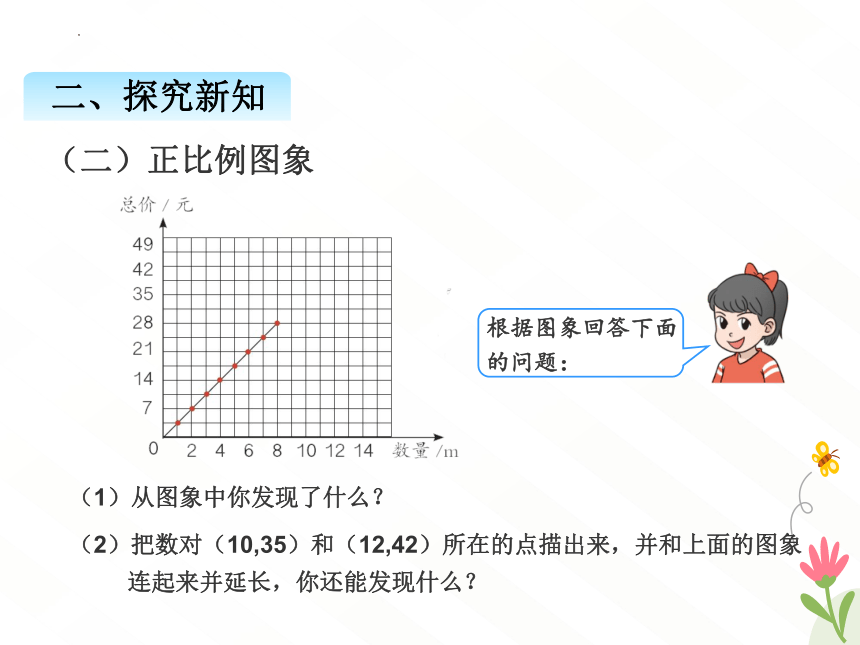
上表中的数据还可以用图象表示。
(二)正比例图象
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
二、探究新知
(1)从图象中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象
连起来并延长,你还能发现什么?
根据图象回答下面的问题:
(二)正比例图象
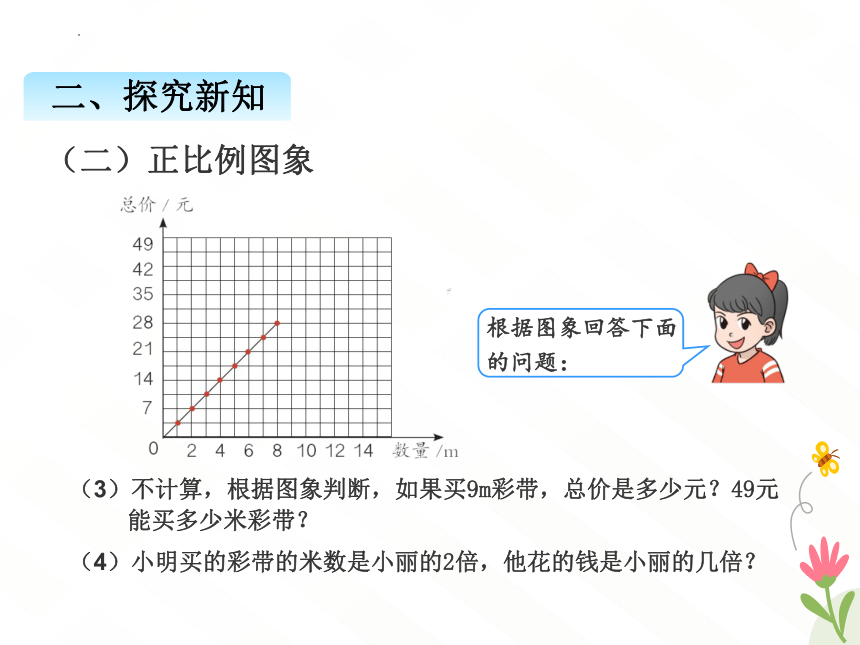
二、探究新知
(3)不计算,根据图象判断,如果买9m彩带,总价是多少元?49元
能买多少米彩带?
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
根据图象回答下面的问题:
二、探究新知
(二)正比例图象
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
(二)正比例图象
二、探究新知
三、巩固练习
1.已知y 与x成正比例关系,在下表的空格中填写合适的数。
x 1 2 5 10 20
y 2.5 7.5 20 37.5
5
3
8
15
12.5
25
50
2. 一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。
=
=
=
=
=
=
80
三、巩固练习
(2)说一说这个比值表示什么。
这个比值表示汽车行驶的速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例关系;因为路程随着时间的变化而变化,且路程和时间对应的两个数比值一定,都等于80。
三、巩固练习
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连接起来。估计一下行驶120km大约要用多长时间。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
三、巩固练习
120
1.5
行驶120km大约需要1.5小时
四、课堂小结
通过这节课的学习,你有什么收获?
20XX
第四单元
比例
人教版数学六年级下册
反比例
正比例和反比例
一、复习导入
判断下面各题中的两种量是否成正比例关系。
(1)三角形的高一定,面积和底。
(2)圆的周长和半径。
(一定)
(一定)
把相同体积的水倒入底面积不同的圆柱形容器,容器的底面积与水的高度的变化情况如下表。
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
(一)例2
二、探究新知
根据上表,回答下面的问题。
(1)表中有哪两种量?
(一)例2
二、探究新知
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
(2)水的高度是怎样随着容器底面积的大小变化而变化的?
表中有两种量,一种是容器的底面积,一种是水的高度。
水的高度随着容器底面积的增大而减小。
二、探究新知
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
(3)相对应的容器的底面积与水的高度的乘积分别是多少?
×
×
×
×
×
=300
实际上就是倒入容器的水的体积
底面积×高度=体积
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
(一)例2
二、探究新知
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),
反比例关系可以用下面的式子表示:
x y=k
你能举出生活中反比例关系的例子吗?
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
(二)反比例举例
二、探究新知
1.判断下面各题中的两种量是否成反比例关系。
(1)汽车的速度一定,行驶的路程和时间。
(2)非零自然数a和它的倒数。
(一定)
(a≠0)
成反比例关系
成正比例关系
三、巩固练习
每天运的质量/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
(1)表中有哪两种量?它们是不是相关联的量?
三、知识应用
表中有每天运的质量和运货的天数这两种量,它们是相关联的量。
运输队要运一批货物,每天运的质量和运货的天数之间的关系如下。
三、知识应用
(2)写出几组这两种量中相对应的两个数的积,并比较积的
大小,说一说这个积表示什么。
每天运的质量/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
300×1
150×2
100×3
=
=
=
300
货物的
总吨数
(3)运货的天数与每天运的质量成反比例关系吗?为什么?
每天运的质量/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
三、知识应用
x
运货的天数
每天运的质量
y
x×y=300
(一定)
成反比例关系
四、课堂小结
通过这节课的学习,你有什么收获?
谢谢观看
20XX
第四单元
比例
人教版数学六年级下册
正比例
正比例和反比例
一、复习导入
已知路程和时间,怎样求速度?
速度=路程÷时间
已知总价和数量,怎样求单价?
单价=总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率=工作总量÷工作时间
这节课我们一起来研究有特殊关系的两种相关联的量。
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)总价是怎样随着数量的变化而变化的?
(3)相应的总价与数量的比分别是多少?比值是多少?
你能发现什么?
二、探究新知
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
从上表可以看出,总价与数量是两种相关联的量,总价随着数量的变化而变化的,而且总价与相应数量的比值总是一定的。
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
二、探究新知
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
单价
…
2
7
例如:
=
=
3.5
1
3.5
3
10.5
=
=
比值3.5,实际就是彩带的单价。用式子表它们的关系就是:
总价
数量
=
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
二、探究新知
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
总价
=
单价
数量
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
文具店有一种彩带,销售的数量与总价的关系如下表。
(一)例1
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
二、探究新知
上表中,总价和数量是成正比例的量,总价与数量成正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
总价
=
单价
数量
文具店有一种彩带,销售的数量与总价的关系如下表。
x
y
= k
(一)例1
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
二、探究新知
文具店有一种彩带,销售的数量与总价的关系如下表。
上表中的数据还可以用图象表示。
(二)正比例图象
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
二、探究新知
(1)从图象中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象
连起来并延长,你还能发现什么?
根据图象回答下面的问题:
(二)正比例图象
二、探究新知
(3)不计算,根据图象判断,如果买9m彩带,总价是多少元?49元
能买多少米彩带?
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
根据图象回答下面的问题:
二、探究新知
(二)正比例图象
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
(二)正比例图象
二、探究新知
三、巩固练习
1.已知y 与x成正比例关系,在下表的空格中填写合适的数。
x 1 2 5 10 20
y 2.5 7.5 20 37.5
5
3
8
15
12.5
25
50
2. 一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。
=
=
=
=
=
=
80
三、巩固练习
(2)说一说这个比值表示什么。
这个比值表示汽车行驶的速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例关系;因为路程随着时间的变化而变化,且路程和时间对应的两个数比值一定,都等于80。
三、巩固练习
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连接起来。估计一下行驶120km大约要用多长时间。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
三、巩固练习
120
1.5
行驶120km大约需要1.5小时
四、课堂小结
通过这节课的学习,你有什么收获?
20XX
第四单元
比例
人教版数学六年级下册
反比例
正比例和反比例
一、复习导入
判断下面各题中的两种量是否成正比例关系。
(1)三角形的高一定,面积和底。
(2)圆的周长和半径。
(一定)
(一定)
把相同体积的水倒入底面积不同的圆柱形容器,容器的底面积与水的高度的变化情况如下表。
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
(一)例2
二、探究新知
根据上表,回答下面的问题。
(1)表中有哪两种量?
(一)例2
二、探究新知
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
(2)水的高度是怎样随着容器底面积的大小变化而变化的?
表中有两种量,一种是容器的底面积,一种是水的高度。
水的高度随着容器底面积的增大而减小。
二、探究新知
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
(3)相对应的容器的底面积与水的高度的乘积分别是多少?
×
×
×
×
×
=300
实际上就是倒入容器的水的体积
底面积×高度=体积
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
(一)例2
二、探究新知
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),
反比例关系可以用下面的式子表示:
x y=k
你能举出生活中反比例关系的例子吗?
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
(二)反比例举例
二、探究新知
1.判断下面各题中的两种量是否成反比例关系。
(1)汽车的速度一定,行驶的路程和时间。
(2)非零自然数a和它的倒数。
(一定)
(a≠0)
成反比例关系
成正比例关系
三、巩固练习
每天运的质量/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
(1)表中有哪两种量?它们是不是相关联的量?
三、知识应用
表中有每天运的质量和运货的天数这两种量,它们是相关联的量。
运输队要运一批货物,每天运的质量和运货的天数之间的关系如下。
三、知识应用
(2)写出几组这两种量中相对应的两个数的积,并比较积的
大小,说一说这个积表示什么。
每天运的质量/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
300×1
150×2
100×3
=
=
=
300
货物的
总吨数
(3)运货的天数与每天运的质量成反比例关系吗?为什么?
每天运的质量/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
三、知识应用
x
运货的天数
每天运的质量
y
x×y=300
(一定)
成反比例关系
四、课堂小结
通过这节课的学习,你有什么收获?
谢谢观看
