2023-2024学年苏教版四年级上册数学第六单元《可能性》单元检测卷(含答案解析)
文档属性
| 名称 | 2023-2024学年苏教版四年级上册数学第六单元《可能性》单元检测卷(含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 685.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览





文档简介
四年级上册数学单元检测卷
第六单元《可能性》
姓名:_________班级:_________学号:_________
注意事项:
1.考试时间:90分钟,试卷满分:100分。答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.选择题、判断题必须使用2B铅笔填涂答案,非选择、判断题必须使用黑色墨迹签字笔或钢笔答题,请将答案填写在答题卡规定的位置上。
3.所有题目必须在答题卡上作答,在试卷上作答无效。
4.考试结束后将试卷和答题卡一并交回。
一、选择题(共16分)
1.奇思问爸爸的年龄,爸爸笑着说:我的年龄( )比你的年龄大。
A.不可能 B.可能 C.一定
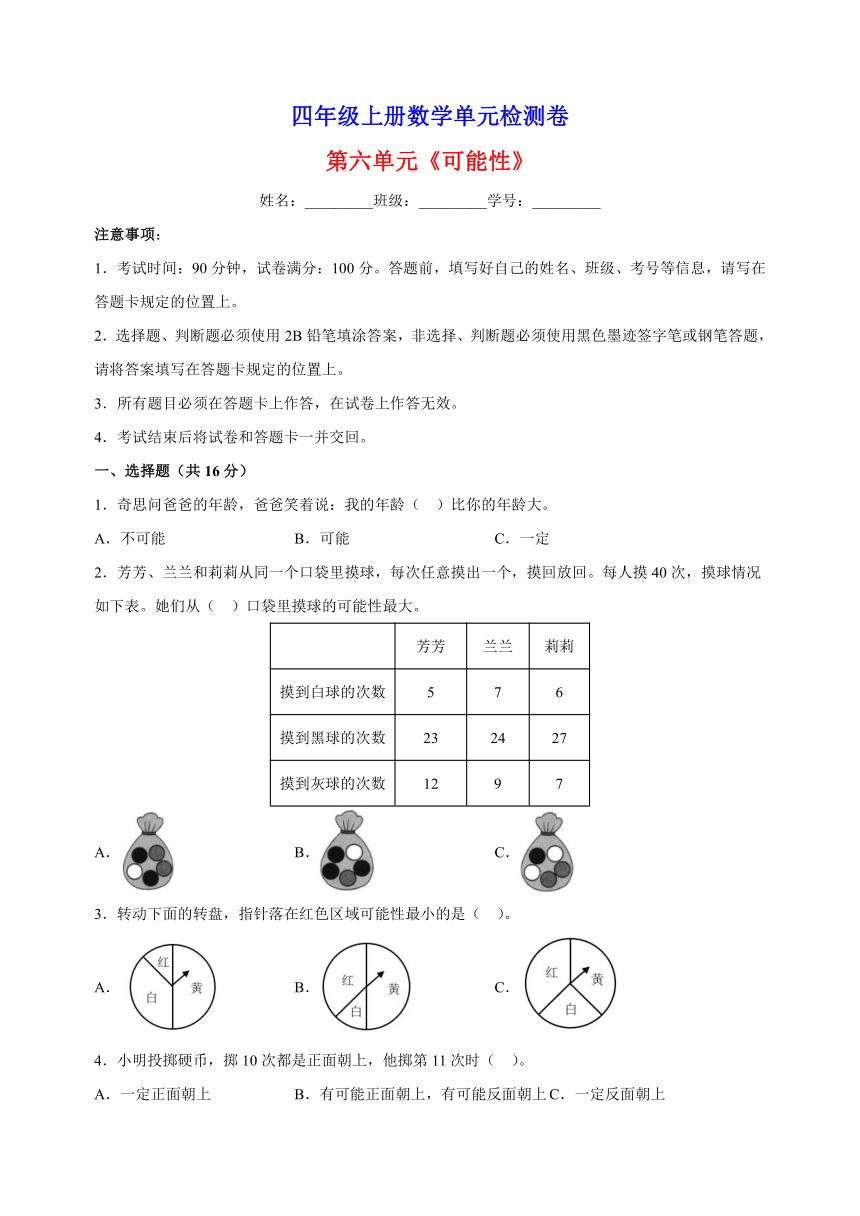
2.芳芳、兰兰和莉莉从同一个口袋里摸球,每次任意摸出一个,摸回放回。每人摸40次,摸球情况如下表。她们从( )口袋里摸球的可能性最大。
芳芳 兰兰 莉莉
摸到白球的次数 5 7 6
摸到黑球的次数 23 24 27
摸到灰球的次数 12 9 7
A. B. C.
3.转动下面的转盘,指针落在红色区域可能性最小的是( )。
A. B. C.
4.小明投掷硬币,掷10次都是正面朝上,他掷第11次时( )。
A.一定正面朝上 B.有可能正面朝上,有可能反面朝上 C.一定反面朝上
5.把同一枚硬币抛掷6次,下列说法正确的是( )。
A.一定有3次正面朝上B.不可能都是正面朝上C.有可能4次正面朝上
6.任意摸一个球,( )盒子一定摸到白球;( )盒子不可能摸到白球。
① ② ③
A.③② B.①② C.①③
7.两人轮流掷小正方体,约定红面朝上算甲赢1分,黄面朝上算乙赢1分。用下面哪组正方体掷是最公平的?( )
A.1红2蓝2绿1黄 B.2红1绿3黄 C.1红3蓝2黄
8.今天是星期四,明天( )是星期五。
A.可能 B.一定 C.不可能
二、填空题(共16分)
9.选叶子。
(1)太阳()从东方升起。
(2)火山()会爆发。
(3)海南岛冬天()下雪。
10.如图,袋子里放了黑、白两种颜色的球,仔细观察并填空。
(1)摸后放回,每次摸到()球的可能性大一些。
(2)一次至少摸出()个球,才能保证其中一定有一个白球。
11.小美在一个盒子里摸了50次球,下面是小美摸球的记录,想一想,小美可能摸的是()号盒子里的球。
颜色 红色 黄色
次数 9 41
12.小丽和小红玩掷骰子游戏,骰子的六个面上分别写着1、2、3、4、5、6,根据落下时朝上面的数决定谁赢谁输,请你设计两个公平的游戏规则。
规则一:________________________________________________________
规则二:________________________________________________________
13.袋子里装有8个红球和3个白球,从中任意摸出一个球,如果要使两种球摸到的可能性相等,那么需要再往袋子里放入()个白球。
14.长凤国贸第六馆商场“双11”期间举行“转转盘得大奖”活动,转盘分为红、黄、蓝三个区域(如图)。如果你是设计活动规则的商场负责人,你会把指针停在_______色区域设为一等奖。说说你的想法:___________________________________。
15.盒子里放有同样大小的球,红球4个,白球6个,蓝球5个。任意摸一个,摸到()球的可能性大,至少再放入()个红球,摸到蓝球的可能性最小。
16.一个不透明的袋中有同种规格的5个白球,4个黑球,任意摸一个球,摸到()球的可能性大,至少摸出()个球,才能保证有一个是白球。
三、判断题(共8分)
17.一个盒子里有1枚红棋,15枚黑棋,任意摸出一枚,一定摸到黑棋。()
18.“3□5÷32”的商可能是两位数,也可能是一位数,并且商是两位数的可能性更大。()
19.同时抛两枚硬币,相同面和不同面朝上的可能性一样。()
20.随意转动转盘,指针停在“黄”字格的可能性最大。()
四、连线题(共18分)
21.(6分)连一连。
22.(6分)连一连。
23.(6分)连线。
五、作图题(共12分)
24.(6分)某超市国庆促销活动,设有四种奖项:一等奖,二等奖,三等奖,和纪念奖。请根据以下条件,在转盘上画出四种奖项的区域。
(1)一等奖可能性最小。
(2)二等奖的可能性小于三等奖。
(3)纪念奖和三等奖的可能性相同。
25.(6分)按要求涂颜色。
摸出的球不可能是黑球。
六、解答题(共30分)
26.(6分)市民乘坐地铁时的支付方式在这几年发生了很大的变化。从现金、卡票、手机支付,再到现在的“刷脸”支付。截至目前,某市地铁线路均已开通刷脸乘车支付方式。下表是工作人员在某个时间点监测到的乘客乘坐地铁支付方式的情况。
你认为下一个乘客可能会选择哪种支付方式?说明理由。
记录 次数
现金 正 5
卡票 正正正正正正 30
手机 正正正正正正正正 40
刷脸 正正正正正正 30
27.(6分)请你用“一定”“可能”或“不可能”分别说一个生活中的现象。
28.(6分)9张卡片上分别标有1~9这9个数字,依依和糕糕利用这9张卡片做游戏。游戏规则如下:依依从中任意抽一张,若抽到的卡片是质数,依依胜,否则糕糕胜。这个游戏公平吗?为什么?如果不公平,设计一个对双方都公平的游戏规则。
29.(6分)妈妈在一个不透明的布袋中放了10个玻璃球,其中5个绿色、3个红色和2个蓝色。如果小明从布袋中一次摸出2个玻璃球,会出现哪些可能的情况?
30.(6分)现在是上午10时,外面正下着大雨,丽丽对梅梅说,“再过12时,太阳一定会出来的”。请你想一想,丽丽说的可能发生吗?为什么?
参考答案
1.C
【分析】根据生活常识,先有爸爸,然后才有奇思,即奇思出生比爸爸晚,那么爸爸的年龄一定比奇思大。
【详解】奇思的年龄一定比爸爸的年龄大。故答案为:C
【点睛】父母的年龄一定是大于孩子的年龄,根据常识解答。
2.B
【分析】当球的个数一定的情况下,哪种颜色的球多,摸到那种颜色的球的可能性就大,反之就少,如果两种颜色的球一样多,则摸到这两种球的可能性相等,据此即可解答。
【详解】根据摸球情况统计表可知,每人摸40次,都是摸到黑球的次数最多,说明口袋中黑球最多,三个选项中,只有B选项符合要求。故答案为:B
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
3.A
【分析】不确定事件发生的可能性的大小与事物的数量有关。数量越多,可能性越大,反之则越小,据此解答即可。
【详解】要使指针停在红色区域可能性最小,说明红色区域面积最小,只有符合;故答案为:A
【点睛】明确不确定事件发生的可能性的大小与事物的数量有关是解答本题的关键。
4.B
【分析】掷硬币只能出现正面朝上和反面朝上两种结果,每种结果朝上的可能性大小一样,每次掷硬币都是一个独立事件,下一次的结果不会受前一次的影响,每种结果朝上的可能性都会发生,据此即可解答。
【详解】根据分析可知,小明投掷硬币,掷10次都是正面朝上,他掷第11次时有可能正面朝上,有可能反面朝上。故答案为:B
【点睛】本题主要考查学生对可能性大小比较知识的掌握和灵活运用。
5.C
【分析】抛硬币有可能正面朝上,也有可能反面朝上,正面朝上和反面朝上的可能性一样大,但每次投掷硬币结果不确定,是随机现象。
【详解】A.抛掷硬币,有可能正面朝上,也有可能反面朝上,把同一枚硬币抛掷6次,有可能6次都是反面朝上,一定有3次正面朝上说法错误;
B.抛掷硬币,有可能正面朝上,也有可能反面朝上,把同一枚硬币抛掷6次,有可能6次都是正面朝上,不可能都是正面朝上说法错误;
C.抛掷硬币,有可能正面朝上,也有可能反面朝上,把同一枚硬币抛掷6次,有可能4次正面朝上,说法正确。
故答案为:C
【点睛】此题考查学生对可能性的理解,解题关键是感受简单的随机现象及其结果发生的可能性。
6.A
【分析】①盒子有白球,也有黑球,任意摸一个球,可能摸到白球,也可能摸到黑球;
②盒子只有黑球,任意摸一个球,一定摸到黑球;
③盒子只有白球,任意摸一个球,一定摸到白球。
【详解】根据分析可知:
任意摸一个球,③盒子一定摸到白球;②盒子不可能摸到白球。故答案为:A
【点睛】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。
在任何情况下,都不会发生的事件,是“不可能”事件。
在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
7.A
【分析】小正方体的6个面中,有红面、蓝面、绿面、黄面,把小正方体抛出去后,数量多的颜色出现的可能性最大,数量少的颜色出现的可能性最小。
【详解】A.把小正方体抛出去后,可能红面朝上,也可能黄面朝上,也可能蓝面朝上,也可能绿面朝上,红面和黄面数量一样,红面和黄面出现的可能性大小相等;
B.把小正方体抛出去后,可能红面朝上,也可能黄面朝上,也可能绿面朝上,黄面的数量大于红面数量,出现黄面的可能性比出现红面的可能性大;
C.把小正方体抛出去后,可能红面朝上,也可能黄面朝上,也可能蓝面朝上,黄面的数量大于红面数量,出现黄面的可能性比出现红面的可能性大。
故答案为:A
【点睛】游戏规则是否公平的关键是看游戏的各方出现的可能性是否相同。
8.B
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件。根据事件的确定性和不确定性进行分析,今天是星期四,明天一定是星期五。
【详解】今天是星期四,明天一定是星期五。
故答案为:B
【点睛】此题考查了事件的确定性和不确定性,应结合实际进行解答。
9.(1)一定
(2)可能
(3)不可能
【分析】(1)太阳东升西落这是自然规律,据此解答;
(2)火山会爆发,属于不确定事件,在一定条件下可能发生,也可能不发生的事件;
(3)根据事件发生的确定性和不确定性进行分析:在海南岛只有春夏2季,不可能下雪,属于确定事件中的不可能事件;据此解答即可。
(1)
太阳一定从东方升起。
(2)
火山可能会爆发。
(3)
海南岛冬天不可能下雪。
【点睛】此题考查了事件发生的确定性和不确定性,应注意灵活应用。
10.(1)黑
(2)4
【分析】根据两种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大;
根据最不利原则,假设前3个摸到的全是黑球,则至少摸4个球,才能保证有一个白球。
【详解】(1)摸后放回,每次摸到黑球的可能性大一些。
(2)一次至少摸出4个球,才能保证其中一定有一个白球。
【点睛】此题考查了可能性解决实际问题的灵活应用以及抽屉原理,解决抽屉原理关键是从最差情况考虑。
11.①
【分析】根据题意,摸出50次球,黄色出现41次,红色出现9次,那么摸出黄球的次数比红球的次数多得多,说明黄球的数量要比红球多得多,据此解答。
【详解】根据分析可知:黄球的数量要比红球多得多,只有①号盒子中黄球的数量要比红球多得多,则小美可能摸的是①号盒子里的球。
【点睛】此题应根据可能性的大小进行分析、解答。
12. 1-3小丽赢,4-6小红赢。单数小丽赢,双数小红赢。
【分析】规则一:朝上的数1-3小丽赢,4-6小红赢;
1-3有1、2、3三种可能,4-6有4、5、6三种可能,双方的机会是均等的,所以说这个游戏规则公平;
规则二:朝上的数是单数算小丽赢,是双数算小红赢;
双数有:2、4、6共3个,单数有1、3、5共3个,双方的机会是均等的,所以说这个游戏规公平。
【详解】根据分析可知:
规则一:1-3小丽赢,4-6小红赢。
规则二:单数小丽赢,双数小红赢。
【点睛】本题考查游戏的公平性,根据双方获胜的可能性大小进行解答。
13.5
【分析】要使两种球摸到的可能性相等,那么红球的个数等于白球的个数;红球有8个,可以再往袋子里放入(8-3)个白球。
【详解】8-3=5(个)
需要再往袋子里放入5个白球。
【点睛】本题主要考查学生对可能性的大小知识的掌握和灵活运用。
14.黄哪个颜色区域的面积越大,指针停在这个区域的可能性就越大,哪个颜色区域的面积越小,指针停在这个区域的可能性就越小,转盘中红色面积最大,蓝色其次,黄色最小,所以指针停在黄色区域设为一等奖。
【分析】哪个颜色区域的面积越大,指针停在这个区域的可能性就越大,哪个颜色区域的面积越小,指针停在这个区域的可能性就越小,一等奖最少,应设在可能性最小区域,据此即可解答。
【详解】哪个颜色区域的面积越大,指针停在这个区域的可能性就越大,哪个颜色区域的面积越小,指针停在这个区域的可能性就越小,转盘中红色面积最大,蓝色其次,黄色最小,所以指针停在黄色区域设为一等奖。
【点睛】本题主要考查了可能性的实际应用,总情况数一定的情况下,谁包含的情况数多,谁的可能性就大。
15.白 2
【分析】哪种颜色的球的数量多,摸到的可能性就大;要想摸到蓝球的可能性最小,就要使蓝球的数量最少,现在是红球数量比蓝球数量少,那么放入后的红球最少应该有5+1=6(个),放入的最少红球数量=放入后的最少数量-4。
【详解】6>5>4,白球的数量最多,红球的数量最少,所以任意摸一个,摸到白球的可能性大。
5+1-4
=6-4
=2(个)
即至少再放入2个红球,摸到蓝球的可能性就最小。
【点睛】在不需要计算可能性大小的准确值时,可以根据各种颜色的球的数量的多少直接判断可能性的大小。
16.白 5
【分析】可以直接根据球的数量的多少来判断,数量多的摸到的可能性就大,数量少的摸到的可能性就小;
要保证有一个是白球,从最不利的情况考虑,先把全部黑球摸出来,第5个才摸到一个白球,据此解答。
【详解】5>4,白球的数量>黑球的数量,则摸到白球的可能性大;
4+1=5(个),至少摸出5个球,才能保证有一个是白球。
【点睛】解决此题关键是如果不需要准确地计算可能性的大小时,可以根据各种球个数的多少,直接判断可能性的大小。
17.×
【分析】从数量上分析,一共1枚红棋和15枚黑棋。从中任意摸出一枚,摸到数量最多的那种棋的可能性最大。要想一定摸到黑棋,盒子里应只有黑棋。据此判断即可。
【详解】一个盒子里有1枚红棋,15枚黑棋,任意摸出一枚,摸到摸到黑棋的可能性最大,但不是一定摸到黑棋。
故答案为:×。
【点睛】可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
18.√
【分析】三位数除以两位数,如果被除数的前两位大于等于除数,商是两位数,否则商是一位数,据此即可解答。
【详解】3□5÷32,如果商是两位数,则3□≥32,□里可以填的数为2、3、4、5、6、7、8、9,共8个;
如果商是一位数,则3□<32,□里可以填的数为0、1,共2个;8个>2个,所以商是两位数的可能性比商是一位数的可能性大。
故答案为:√
【点睛】本题主要考查学生对整数除法试商方法和可能性大小知识的掌握。
19.√
【分析】硬币只有2个面,要么正面朝上要么反面朝上,两种的可能性是相同的。
【详解】同时抛两枚硬币,相同面和不同面朝上的可能性一样,这句话是对的。
故答案为:√
【点睛】可能性的大小,比较面的个数,若个数相同,可能性一样大。
20.√
【分析】随意转动转盘,指针可能停在“黄”字格,也可能停在“红”字格,也可能停在“绿”字格,“黄”字格的格数最多,指针停在“黄”字格的可能性最大。
【详解】随意转动转盘,指针停在“黄”字格的可能性最大。
故答案为:√
【点睛】本题考查可能性大小的判断,解题关键是理解并掌握影响可能性大小的因素,理解哪种颜色的格子多,停在哪种颜色格的可能性就大。
21.见详解
【分析】由题目可知,根据事件发生的确定性和不确定性进行分析:
公鸡不会下蛋是客观规律,所以是确定现象;
太阳从东方升起,是客观规律,属于确定事件中的必然事件,是一定的,所以是确定现象;
小丽数学考试的成绩属于不确定事件的可能事件;
儿童必须补充水分,所以儿童需要喝水是确定现象;
小乌龟在陆地上玩是在一定情况下可能发生,也可能不发生,所以是不确定现象;
明天的天气情况属于不确定事件中的可能事件,是可能的。
【详解】由分析可知:
【点睛】此题考查的是事件的确定性和不确定性,需熟练掌握。
22.见详解
【分析】①中只有△,所以一定能摸出△,不可能摸出▲;②中有3个△和3个▲,所以可能摸出△,也可能摸出▲;③中只有▲,所以一定能摸出▲,不可能摸出△;据此连线。
【详解】根据分析连线如下:
【点睛】本题主要考查事件的确定性和不确定性,熟练掌握什么是一定发生的情况,什么是不可能发生的情况。
23.见详解
【分析】只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相等,那么它们的可能性就相等,如果没有包含该情况就不可能发生,如果包含的全部是该情况就一定能发生。
【详解】
【点睛】主要考查学生对可能性大小比较知识的掌握和灵活运用。
24.见详解
【分析】根据哪个奖项的数量越多,则抽到该奖项的可能性就越大。
(1)因为一等奖可能性最小,所以可以让一等奖占其中的1份。
(2)因为二等奖的可能性小于三等奖,所以可以让二等奖占其中的2份,三等奖占其中的4份。
(3)因为纪念奖和三等奖的可能性相同,所以让纪念奖和三等奖各占其中的4份。
【详解】
【点睛】不需要计算可能性的大小的准确值时,可以根据各种奖项数量的多少,直接判断可能性的大小。
25.见详解
【分析】根据摸出的球不可能是黑球,则盒子里没有黑球,据此解答即可。
【详解】
(答案不唯一)
【点睛】根据事件的确定性和不确定性的知识,解答此题即可。
26.见详解
【分析】从记录表中可知,现金支付的有5次,卡票支付的有30次,手机支付的有40次,刷脸支付的有30次;40次>30次>5次,手机支付的人数最多,则下一个乘客选择手机支付的可能性最大。
【详解】答:下一个乘客可能会选择手机支付方式;理由:根据各种支付方式的记录结果可以判断,用手机支付的人数是最多的,所以下一个乘客选择手机支付的可能性最大。
【点睛】本题主要考查学生对可能性的大小知识的掌握和灵活运用。
27.掷一枚骰子,朝上的数一定小于7。两人下象棋,可能平局。梨树上不可能结草莓。
【分析】根据生活经验,说出有关“一定”、“可能”和“不可能”这三个字眼的现象。答案不唯一,合理即可。
【详解】答:掷一枚骰子,朝上的数一定小于7。两人下象棋,可能平局。梨树上不可能结草莓。
【点睛】本题主要考查的是事件的确定现象与不确定现象,解题关键在于学生对生活现象的观察。
28.见详解
【分析】结合质数、合数知识,首先明确在1~9这9个数字中,质数有2,3,5,7共4个,不是质数的有1,4,6,8,9共5个,然后判断规则是否公平,然后制定公平合理的规则即可。
【详解】这个游戏规则不公平,因为在1~9这9个数字中,质数有2,3,5,7共4个,不是质数的有1,4,6,8,9共5个,所以这个游戏不公平。
对双方都公平的游戏规则:若抽到的卡片数字是质数,则依依获胜,若抽到的卡片数字是合数,则糕糕获胜,抽到1重新抽。(游戏规则不唯一)
【点睛】本题考查了游戏规则的公平性知识,结合质数、合数知识,进行分析解答即可。
29.2个绿球;2个红球;2个蓝球;1个绿球1个红球;1个绿球1个蓝球;1个红球1个蓝球
【分析】这10个玻璃球有3种,从中一次摸出2个玻璃球,摸出的玻璃球可以是一种,也可以是两种。据此依次列出所有可能的情况。
【详解】可以摸出2个绿球;2个红球;2个蓝球;1个绿球1个红球;1个绿球1个蓝球;1个红球1个蓝球,共有6种情况。
【点睛】本题考查事件的确定性与不确定性,关键是按照摸出一种玻璃球或者摸出两种玻璃球这两种情况解答。
30.不可能发生。理由见详解
【分析】由题意可知,先用上午10时加上12个小时,看再过12小时是什么时间,根据所得时间判断是否可能会出现太阳,据此解答。
【详解】10时+12时=22时
22时是晚上10点
因此不可能发生。
答:不可能发生。因为现在时间是上午10时,再过12时是晚上22时,太阳一定不会出来。
【点睛】本题考查的是不确定现象,根据时间的加法运算得出题目所表述的时间,结果具有确定性,结合生活实际,进而得出结论。
第六单元《可能性》
姓名:_________班级:_________学号:_________
注意事项:
1.考试时间:90分钟,试卷满分:100分。答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.选择题、判断题必须使用2B铅笔填涂答案,非选择、判断题必须使用黑色墨迹签字笔或钢笔答题,请将答案填写在答题卡规定的位置上。
3.所有题目必须在答题卡上作答,在试卷上作答无效。
4.考试结束后将试卷和答题卡一并交回。
一、选择题(共16分)
1.奇思问爸爸的年龄,爸爸笑着说:我的年龄( )比你的年龄大。
A.不可能 B.可能 C.一定
2.芳芳、兰兰和莉莉从同一个口袋里摸球,每次任意摸出一个,摸回放回。每人摸40次,摸球情况如下表。她们从( )口袋里摸球的可能性最大。
芳芳 兰兰 莉莉
摸到白球的次数 5 7 6
摸到黑球的次数 23 24 27
摸到灰球的次数 12 9 7
A. B. C.
3.转动下面的转盘,指针落在红色区域可能性最小的是( )。
A. B. C.
4.小明投掷硬币,掷10次都是正面朝上,他掷第11次时( )。
A.一定正面朝上 B.有可能正面朝上,有可能反面朝上 C.一定反面朝上
5.把同一枚硬币抛掷6次,下列说法正确的是( )。
A.一定有3次正面朝上B.不可能都是正面朝上C.有可能4次正面朝上
6.任意摸一个球,( )盒子一定摸到白球;( )盒子不可能摸到白球。
① ② ③
A.③② B.①② C.①③
7.两人轮流掷小正方体,约定红面朝上算甲赢1分,黄面朝上算乙赢1分。用下面哪组正方体掷是最公平的?( )
A.1红2蓝2绿1黄 B.2红1绿3黄 C.1红3蓝2黄
8.今天是星期四,明天( )是星期五。
A.可能 B.一定 C.不可能
二、填空题(共16分)
9.选叶子。
(1)太阳()从东方升起。
(2)火山()会爆发。
(3)海南岛冬天()下雪。
10.如图,袋子里放了黑、白两种颜色的球,仔细观察并填空。
(1)摸后放回,每次摸到()球的可能性大一些。
(2)一次至少摸出()个球,才能保证其中一定有一个白球。
11.小美在一个盒子里摸了50次球,下面是小美摸球的记录,想一想,小美可能摸的是()号盒子里的球。
颜色 红色 黄色
次数 9 41
12.小丽和小红玩掷骰子游戏,骰子的六个面上分别写着1、2、3、4、5、6,根据落下时朝上面的数决定谁赢谁输,请你设计两个公平的游戏规则。
规则一:________________________________________________________
规则二:________________________________________________________
13.袋子里装有8个红球和3个白球,从中任意摸出一个球,如果要使两种球摸到的可能性相等,那么需要再往袋子里放入()个白球。
14.长凤国贸第六馆商场“双11”期间举行“转转盘得大奖”活动,转盘分为红、黄、蓝三个区域(如图)。如果你是设计活动规则的商场负责人,你会把指针停在_______色区域设为一等奖。说说你的想法:___________________________________。
15.盒子里放有同样大小的球,红球4个,白球6个,蓝球5个。任意摸一个,摸到()球的可能性大,至少再放入()个红球,摸到蓝球的可能性最小。
16.一个不透明的袋中有同种规格的5个白球,4个黑球,任意摸一个球,摸到()球的可能性大,至少摸出()个球,才能保证有一个是白球。
三、判断题(共8分)
17.一个盒子里有1枚红棋,15枚黑棋,任意摸出一枚,一定摸到黑棋。()
18.“3□5÷32”的商可能是两位数,也可能是一位数,并且商是两位数的可能性更大。()
19.同时抛两枚硬币,相同面和不同面朝上的可能性一样。()
20.随意转动转盘,指针停在“黄”字格的可能性最大。()
四、连线题(共18分)
21.(6分)连一连。
22.(6分)连一连。
23.(6分)连线。
五、作图题(共12分)
24.(6分)某超市国庆促销活动,设有四种奖项:一等奖,二等奖,三等奖,和纪念奖。请根据以下条件,在转盘上画出四种奖项的区域。
(1)一等奖可能性最小。
(2)二等奖的可能性小于三等奖。
(3)纪念奖和三等奖的可能性相同。
25.(6分)按要求涂颜色。
摸出的球不可能是黑球。
六、解答题(共30分)
26.(6分)市民乘坐地铁时的支付方式在这几年发生了很大的变化。从现金、卡票、手机支付,再到现在的“刷脸”支付。截至目前,某市地铁线路均已开通刷脸乘车支付方式。下表是工作人员在某个时间点监测到的乘客乘坐地铁支付方式的情况。
你认为下一个乘客可能会选择哪种支付方式?说明理由。
记录 次数
现金 正 5
卡票 正正正正正正 30
手机 正正正正正正正正 40
刷脸 正正正正正正 30
27.(6分)请你用“一定”“可能”或“不可能”分别说一个生活中的现象。
28.(6分)9张卡片上分别标有1~9这9个数字,依依和糕糕利用这9张卡片做游戏。游戏规则如下:依依从中任意抽一张,若抽到的卡片是质数,依依胜,否则糕糕胜。这个游戏公平吗?为什么?如果不公平,设计一个对双方都公平的游戏规则。
29.(6分)妈妈在一个不透明的布袋中放了10个玻璃球,其中5个绿色、3个红色和2个蓝色。如果小明从布袋中一次摸出2个玻璃球,会出现哪些可能的情况?
30.(6分)现在是上午10时,外面正下着大雨,丽丽对梅梅说,“再过12时,太阳一定会出来的”。请你想一想,丽丽说的可能发生吗?为什么?
参考答案
1.C
【分析】根据生活常识,先有爸爸,然后才有奇思,即奇思出生比爸爸晚,那么爸爸的年龄一定比奇思大。
【详解】奇思的年龄一定比爸爸的年龄大。故答案为:C
【点睛】父母的年龄一定是大于孩子的年龄,根据常识解答。
2.B
【分析】当球的个数一定的情况下,哪种颜色的球多,摸到那种颜色的球的可能性就大,反之就少,如果两种颜色的球一样多,则摸到这两种球的可能性相等,据此即可解答。
【详解】根据摸球情况统计表可知,每人摸40次,都是摸到黑球的次数最多,说明口袋中黑球最多,三个选项中,只有B选项符合要求。故答案为:B
【点睛】本题主要考查学生对可能性知识的掌握和灵活运用。
3.A
【分析】不确定事件发生的可能性的大小与事物的数量有关。数量越多,可能性越大,反之则越小,据此解答即可。
【详解】要使指针停在红色区域可能性最小,说明红色区域面积最小,只有符合;故答案为:A
【点睛】明确不确定事件发生的可能性的大小与事物的数量有关是解答本题的关键。
4.B
【分析】掷硬币只能出现正面朝上和反面朝上两种结果,每种结果朝上的可能性大小一样,每次掷硬币都是一个独立事件,下一次的结果不会受前一次的影响,每种结果朝上的可能性都会发生,据此即可解答。
【详解】根据分析可知,小明投掷硬币,掷10次都是正面朝上,他掷第11次时有可能正面朝上,有可能反面朝上。故答案为:B
【点睛】本题主要考查学生对可能性大小比较知识的掌握和灵活运用。
5.C
【分析】抛硬币有可能正面朝上,也有可能反面朝上,正面朝上和反面朝上的可能性一样大,但每次投掷硬币结果不确定,是随机现象。
【详解】A.抛掷硬币,有可能正面朝上,也有可能反面朝上,把同一枚硬币抛掷6次,有可能6次都是反面朝上,一定有3次正面朝上说法错误;
B.抛掷硬币,有可能正面朝上,也有可能反面朝上,把同一枚硬币抛掷6次,有可能6次都是正面朝上,不可能都是正面朝上说法错误;
C.抛掷硬币,有可能正面朝上,也有可能反面朝上,把同一枚硬币抛掷6次,有可能4次正面朝上,说法正确。
故答案为:C
【点睛】此题考查学生对可能性的理解,解题关键是感受简单的随机现象及其结果发生的可能性。
6.A
【分析】①盒子有白球,也有黑球,任意摸一个球,可能摸到白球,也可能摸到黑球;
②盒子只有黑球,任意摸一个球,一定摸到黑球;
③盒子只有白球,任意摸一个球,一定摸到白球。
【详解】根据分析可知:
任意摸一个球,③盒子一定摸到白球;②盒子不可能摸到白球。故答案为:A
【点睛】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。
在任何情况下,都不会发生的事件,是“不可能”事件。
在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
7.A
【分析】小正方体的6个面中,有红面、蓝面、绿面、黄面,把小正方体抛出去后,数量多的颜色出现的可能性最大,数量少的颜色出现的可能性最小。
【详解】A.把小正方体抛出去后,可能红面朝上,也可能黄面朝上,也可能蓝面朝上,也可能绿面朝上,红面和黄面数量一样,红面和黄面出现的可能性大小相等;
B.把小正方体抛出去后,可能红面朝上,也可能黄面朝上,也可能绿面朝上,黄面的数量大于红面数量,出现黄面的可能性比出现红面的可能性大;
C.把小正方体抛出去后,可能红面朝上,也可能黄面朝上,也可能蓝面朝上,黄面的数量大于红面数量,出现黄面的可能性比出现红面的可能性大。
故答案为:A
【点睛】游戏规则是否公平的关键是看游戏的各方出现的可能性是否相同。
8.B
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件。根据事件的确定性和不确定性进行分析,今天是星期四,明天一定是星期五。
【详解】今天是星期四,明天一定是星期五。
故答案为:B
【点睛】此题考查了事件的确定性和不确定性,应结合实际进行解答。
9.(1)一定
(2)可能
(3)不可能
【分析】(1)太阳东升西落这是自然规律,据此解答;
(2)火山会爆发,属于不确定事件,在一定条件下可能发生,也可能不发生的事件;
(3)根据事件发生的确定性和不确定性进行分析:在海南岛只有春夏2季,不可能下雪,属于确定事件中的不可能事件;据此解答即可。
(1)
太阳一定从东方升起。
(2)
火山可能会爆发。
(3)
海南岛冬天不可能下雪。
【点睛】此题考查了事件发生的确定性和不确定性,应注意灵活应用。
10.(1)黑
(2)4
【分析】根据两种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大;
根据最不利原则,假设前3个摸到的全是黑球,则至少摸4个球,才能保证有一个白球。
【详解】(1)摸后放回,每次摸到黑球的可能性大一些。
(2)一次至少摸出4个球,才能保证其中一定有一个白球。
【点睛】此题考查了可能性解决实际问题的灵活应用以及抽屉原理,解决抽屉原理关键是从最差情况考虑。
11.①
【分析】根据题意,摸出50次球,黄色出现41次,红色出现9次,那么摸出黄球的次数比红球的次数多得多,说明黄球的数量要比红球多得多,据此解答。
【详解】根据分析可知:黄球的数量要比红球多得多,只有①号盒子中黄球的数量要比红球多得多,则小美可能摸的是①号盒子里的球。
【点睛】此题应根据可能性的大小进行分析、解答。
12. 1-3小丽赢,4-6小红赢。单数小丽赢,双数小红赢。
【分析】规则一:朝上的数1-3小丽赢,4-6小红赢;
1-3有1、2、3三种可能,4-6有4、5、6三种可能,双方的机会是均等的,所以说这个游戏规则公平;
规则二:朝上的数是单数算小丽赢,是双数算小红赢;
双数有:2、4、6共3个,单数有1、3、5共3个,双方的机会是均等的,所以说这个游戏规公平。
【详解】根据分析可知:
规则一:1-3小丽赢,4-6小红赢。
规则二:单数小丽赢,双数小红赢。
【点睛】本题考查游戏的公平性,根据双方获胜的可能性大小进行解答。
13.5
【分析】要使两种球摸到的可能性相等,那么红球的个数等于白球的个数;红球有8个,可以再往袋子里放入(8-3)个白球。
【详解】8-3=5(个)
需要再往袋子里放入5个白球。
【点睛】本题主要考查学生对可能性的大小知识的掌握和灵活运用。
14.黄哪个颜色区域的面积越大,指针停在这个区域的可能性就越大,哪个颜色区域的面积越小,指针停在这个区域的可能性就越小,转盘中红色面积最大,蓝色其次,黄色最小,所以指针停在黄色区域设为一等奖。
【分析】哪个颜色区域的面积越大,指针停在这个区域的可能性就越大,哪个颜色区域的面积越小,指针停在这个区域的可能性就越小,一等奖最少,应设在可能性最小区域,据此即可解答。
【详解】哪个颜色区域的面积越大,指针停在这个区域的可能性就越大,哪个颜色区域的面积越小,指针停在这个区域的可能性就越小,转盘中红色面积最大,蓝色其次,黄色最小,所以指针停在黄色区域设为一等奖。
【点睛】本题主要考查了可能性的实际应用,总情况数一定的情况下,谁包含的情况数多,谁的可能性就大。
15.白 2
【分析】哪种颜色的球的数量多,摸到的可能性就大;要想摸到蓝球的可能性最小,就要使蓝球的数量最少,现在是红球数量比蓝球数量少,那么放入后的红球最少应该有5+1=6(个),放入的最少红球数量=放入后的最少数量-4。
【详解】6>5>4,白球的数量最多,红球的数量最少,所以任意摸一个,摸到白球的可能性大。
5+1-4
=6-4
=2(个)
即至少再放入2个红球,摸到蓝球的可能性就最小。
【点睛】在不需要计算可能性大小的准确值时,可以根据各种颜色的球的数量的多少直接判断可能性的大小。
16.白 5
【分析】可以直接根据球的数量的多少来判断,数量多的摸到的可能性就大,数量少的摸到的可能性就小;
要保证有一个是白球,从最不利的情况考虑,先把全部黑球摸出来,第5个才摸到一个白球,据此解答。
【详解】5>4,白球的数量>黑球的数量,则摸到白球的可能性大;
4+1=5(个),至少摸出5个球,才能保证有一个是白球。
【点睛】解决此题关键是如果不需要准确地计算可能性的大小时,可以根据各种球个数的多少,直接判断可能性的大小。
17.×
【分析】从数量上分析,一共1枚红棋和15枚黑棋。从中任意摸出一枚,摸到数量最多的那种棋的可能性最大。要想一定摸到黑棋,盒子里应只有黑棋。据此判断即可。
【详解】一个盒子里有1枚红棋,15枚黑棋,任意摸出一枚,摸到摸到黑棋的可能性最大,但不是一定摸到黑棋。
故答案为:×。
【点睛】可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
18.√
【分析】三位数除以两位数,如果被除数的前两位大于等于除数,商是两位数,否则商是一位数,据此即可解答。
【详解】3□5÷32,如果商是两位数,则3□≥32,□里可以填的数为2、3、4、5、6、7、8、9,共8个;
如果商是一位数,则3□<32,□里可以填的数为0、1,共2个;8个>2个,所以商是两位数的可能性比商是一位数的可能性大。
故答案为:√
【点睛】本题主要考查学生对整数除法试商方法和可能性大小知识的掌握。
19.√
【分析】硬币只有2个面,要么正面朝上要么反面朝上,两种的可能性是相同的。
【详解】同时抛两枚硬币,相同面和不同面朝上的可能性一样,这句话是对的。
故答案为:√
【点睛】可能性的大小,比较面的个数,若个数相同,可能性一样大。
20.√
【分析】随意转动转盘,指针可能停在“黄”字格,也可能停在“红”字格,也可能停在“绿”字格,“黄”字格的格数最多,指针停在“黄”字格的可能性最大。
【详解】随意转动转盘,指针停在“黄”字格的可能性最大。
故答案为:√
【点睛】本题考查可能性大小的判断,解题关键是理解并掌握影响可能性大小的因素,理解哪种颜色的格子多,停在哪种颜色格的可能性就大。
21.见详解
【分析】由题目可知,根据事件发生的确定性和不确定性进行分析:
公鸡不会下蛋是客观规律,所以是确定现象;
太阳从东方升起,是客观规律,属于确定事件中的必然事件,是一定的,所以是确定现象;
小丽数学考试的成绩属于不确定事件的可能事件;
儿童必须补充水分,所以儿童需要喝水是确定现象;
小乌龟在陆地上玩是在一定情况下可能发生,也可能不发生,所以是不确定现象;
明天的天气情况属于不确定事件中的可能事件,是可能的。
【详解】由分析可知:
【点睛】此题考查的是事件的确定性和不确定性,需熟练掌握。
22.见详解
【分析】①中只有△,所以一定能摸出△,不可能摸出▲;②中有3个△和3个▲,所以可能摸出△,也可能摸出▲;③中只有▲,所以一定能摸出▲,不可能摸出△;据此连线。
【详解】根据分析连线如下:
【点睛】本题主要考查事件的确定性和不确定性,熟练掌握什么是一定发生的情况,什么是不可能发生的情况。
23.见详解
【分析】只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相等,那么它们的可能性就相等,如果没有包含该情况就不可能发生,如果包含的全部是该情况就一定能发生。
【详解】
【点睛】主要考查学生对可能性大小比较知识的掌握和灵活运用。
24.见详解
【分析】根据哪个奖项的数量越多,则抽到该奖项的可能性就越大。
(1)因为一等奖可能性最小,所以可以让一等奖占其中的1份。
(2)因为二等奖的可能性小于三等奖,所以可以让二等奖占其中的2份,三等奖占其中的4份。
(3)因为纪念奖和三等奖的可能性相同,所以让纪念奖和三等奖各占其中的4份。
【详解】
【点睛】不需要计算可能性的大小的准确值时,可以根据各种奖项数量的多少,直接判断可能性的大小。
25.见详解
【分析】根据摸出的球不可能是黑球,则盒子里没有黑球,据此解答即可。
【详解】
(答案不唯一)
【点睛】根据事件的确定性和不确定性的知识,解答此题即可。
26.见详解
【分析】从记录表中可知,现金支付的有5次,卡票支付的有30次,手机支付的有40次,刷脸支付的有30次;40次>30次>5次,手机支付的人数最多,则下一个乘客选择手机支付的可能性最大。
【详解】答:下一个乘客可能会选择手机支付方式;理由:根据各种支付方式的记录结果可以判断,用手机支付的人数是最多的,所以下一个乘客选择手机支付的可能性最大。
【点睛】本题主要考查学生对可能性的大小知识的掌握和灵活运用。
27.掷一枚骰子,朝上的数一定小于7。两人下象棋,可能平局。梨树上不可能结草莓。
【分析】根据生活经验,说出有关“一定”、“可能”和“不可能”这三个字眼的现象。答案不唯一,合理即可。
【详解】答:掷一枚骰子,朝上的数一定小于7。两人下象棋,可能平局。梨树上不可能结草莓。
【点睛】本题主要考查的是事件的确定现象与不确定现象,解题关键在于学生对生活现象的观察。
28.见详解
【分析】结合质数、合数知识,首先明确在1~9这9个数字中,质数有2,3,5,7共4个,不是质数的有1,4,6,8,9共5个,然后判断规则是否公平,然后制定公平合理的规则即可。
【详解】这个游戏规则不公平,因为在1~9这9个数字中,质数有2,3,5,7共4个,不是质数的有1,4,6,8,9共5个,所以这个游戏不公平。
对双方都公平的游戏规则:若抽到的卡片数字是质数,则依依获胜,若抽到的卡片数字是合数,则糕糕获胜,抽到1重新抽。(游戏规则不唯一)
【点睛】本题考查了游戏规则的公平性知识,结合质数、合数知识,进行分析解答即可。
29.2个绿球;2个红球;2个蓝球;1个绿球1个红球;1个绿球1个蓝球;1个红球1个蓝球
【分析】这10个玻璃球有3种,从中一次摸出2个玻璃球,摸出的玻璃球可以是一种,也可以是两种。据此依次列出所有可能的情况。
【详解】可以摸出2个绿球;2个红球;2个蓝球;1个绿球1个红球;1个绿球1个蓝球;1个红球1个蓝球,共有6种情况。
【点睛】本题考查事件的确定性与不确定性,关键是按照摸出一种玻璃球或者摸出两种玻璃球这两种情况解答。
30.不可能发生。理由见详解
【分析】由题意可知,先用上午10时加上12个小时,看再过12小时是什么时间,根据所得时间判断是否可能会出现太阳,据此解答。
【详解】10时+12时=22时
22时是晚上10点
因此不可能发生。
答:不可能发生。因为现在时间是上午10时,再过12时是晚上22时,太阳一定不会出来。
【点睛】本题考查的是不确定现象,根据时间的加法运算得出题目所表述的时间,结果具有确定性,结合生活实际,进而得出结论。
