2023年湖南省常德市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖南省常德市数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年湖南省常德市数学中考真题名师详解版
考生注意:
1.请考生在试题卷首填写好准考证号及姓名.
2.请将答案填写在答题卡上,填写在试题卷上的无效。
3.本学科试题卷共4页,七道大题,满分120分,考试时量120分钟.
一、选择题(本大题8个小题,每小题3分,满分24分)
1. 的相反数是( )
A. B. C. D.
2. 下面算法正确的是( )
A. B. C. D.
3. 不等式组的解集是( )
A. B. C. D.
4. 我市“神十五”航天员张陆和他的两位战友已于2023年6月4日回到地球家园,“神十六”的三位航天员已在中国空间站开始值守,空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱,假设“神十六”甲、乙、丙三名航天员从核心舱进入问天实验舱和梦天实验舱开展实验的机会均等,现在要从这三名航天员中选2人各进入一个实验舱开展科学实验,则甲、乙两人同时被选中的概率为( )
A. B. C. D.
5. 若,则( )
A. 5 B. 1 C. D. 0
6. 下列命题正确的是( )
A. 正方形的对角线相等且互相平分 B. 对角互补的四边形是平行四边形
C. 矩形的对角线互相垂直 D. 一组邻边相等的四边形是菱形
7. 如图1,在正方形中,对角线相交于点O,E,F分别为,上的一点,且,连接.若,则的度数为( )
A. B. C. D.
8. 观察下边的数表(横排为行,竖排为列),按数表中的规律,分数若排在第a行b列,则的值为( )
……
A. 2003 B. 2004 C. 2022 D. 2023
二、填空题(本大题8个小题,每小题3分,满分24分)
9. 计算:(a2b)3=___.
10. 分解因式:_______.
11. 要使二次根式有意义,则x应满足的条件是__________.
12. 联合国2022年11月15日宣布,全世界人口已达80亿.将8000000000用科学记数法表示为__________.
13. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是_________.
14. 我市体育中考有必考和选考项目,掷实心球是必考项目之一,在一次训练中,张华同学掷实心球10次成绩依次是(单位:米)7.6,8.5,8.6,8.5,9.1,8.5,8.4,8.6,9.2,73.则张华同学撰实心球成绩的众数是__________.
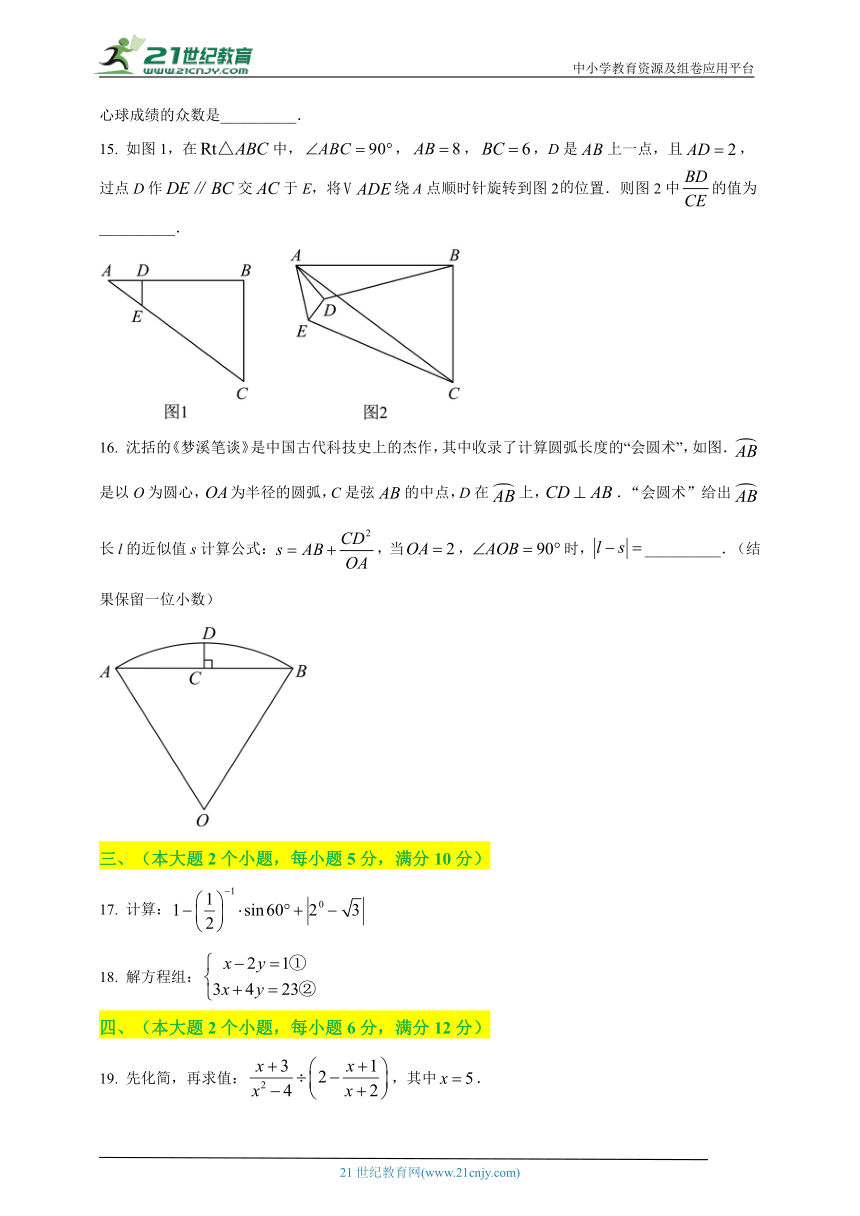
15. 如图1,在中,,,,D是上一点,且,过点D作交于E,将绕A点顺时针旋转到图2位置.则图2中的值为__________.
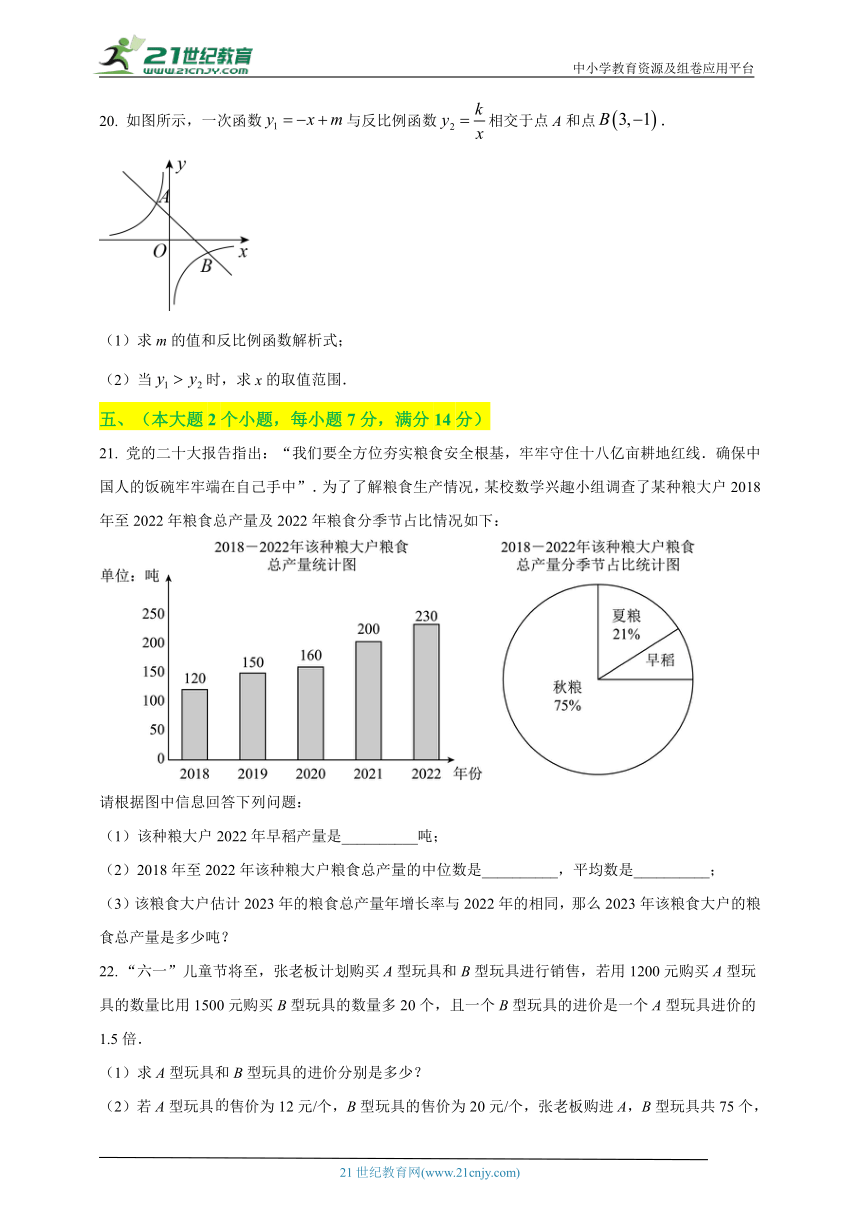
16. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上,.“会圆术”给出长l的近似值s计算公式:,当,时,__________.(结果保留一位小数)
三、(本大题2个小题,每小题5分,满分10分)
17. 计算:
18. 解方程组:
四、(本大题2个小题,每小题6分,满分12分)
19. 先化简,再求值:,其中.
20. 如图所示,一次函数与反比例函数相交于点A和点.
(1)求m的值和反比例函数解析式;
(2)当时,求x的取值范围.
五、(本大题2个小题,每小题7分,满分14分)
21. 党的二十大报告指出:“我们要全方位夯实粮食安全根基,牢牢守住十八亿亩耕地红线.确保中国人的饭碗牢牢端在自己手中”.为了了解粮食生产情况,某校数学兴趣小组调查了某种粮大户2018年至2022年粮食总产量及2022年粮食分季节占比情况如下:
请根据图中信息回答下列问题:
(1)该种粮大户2022年早稻产量是__________吨;
(2)2018年至2022年该种粮大户粮食总产量的中位数是__________,平均数是__________;
(3)该粮食大户估计2023年的粮食总产量年增长率与2022年的相同,那么2023年该粮食大户的粮食总产量是多少吨?
22. “六一”儿童节将至,张老板计划购买A型玩具和B型玩具进行销售,若用1200元购买A型玩具的数量比用1500元购买B型玩具的数量多20个,且一个B型玩具的进价是一个A型玩具进价的1.5倍.
(1)求A型玩具和B型玩具的进价分别是多少?
(2)若A型玩具售价为12元/个,B型玩具的售价为20元/个,张老板购进A,B型玩具共75个,要使总利润不低于300元,则A型玩具最多购进多少个?
六、(本大题2个小题,每小题8分,满分16分)
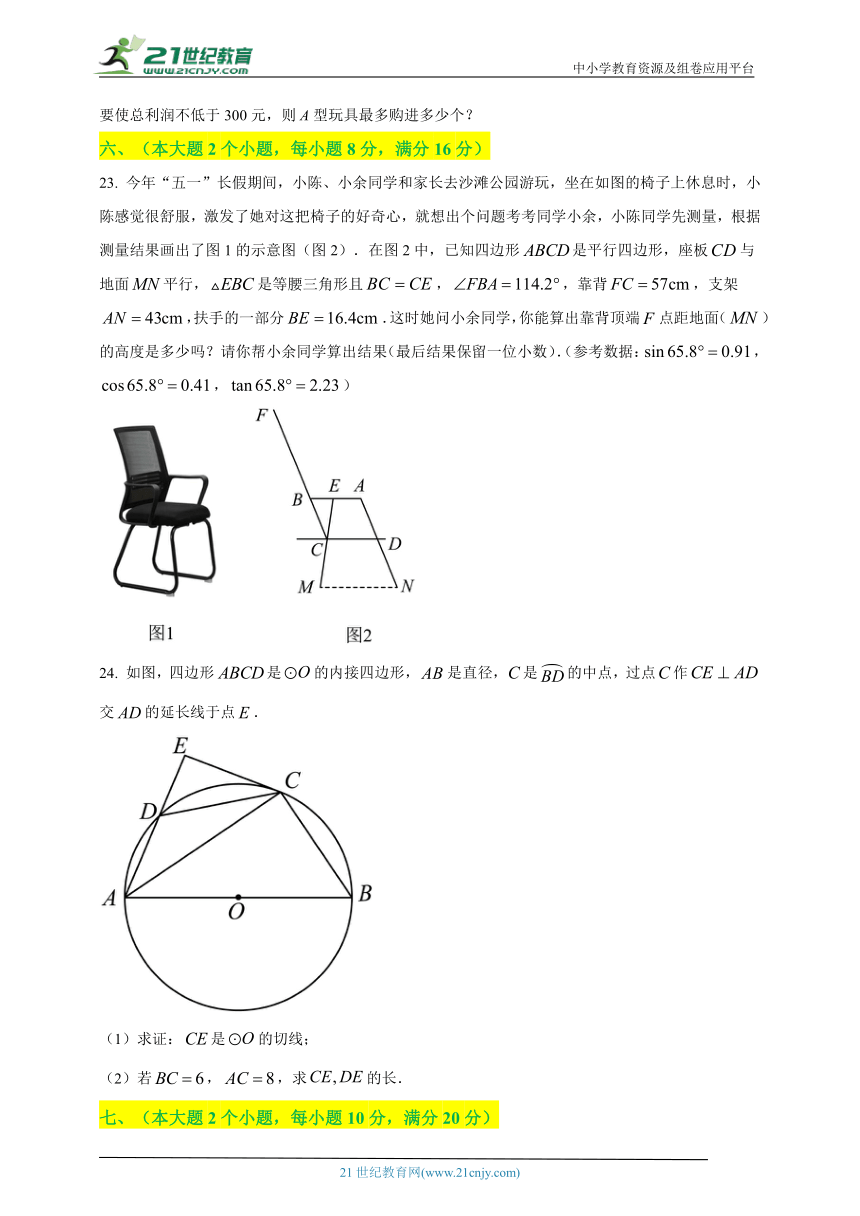
23. 今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且,,靠背,支架,扶手的一部分.这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:,,)
24. 如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
七、(本大题2个小题,每小题10分,满分20分)
25. 如图,二次函数的图象与x轴交于,两点,与y轴交于点C,顶点为D.O为坐标原点,.
(1)求二次函数的表达式;
(2)求四边形的面积;
(3)P是抛物线上的一点,且在第一象限内,若,求P点的坐标.
26. 如图,在中,,D是中点,延长至E,连接.
(1)求证:;
(2)在如图1中,若,其它条件不变得到图2,在图2中过点D作于F,设H是中点,过点H作交于G,交于M.
求证:
①;
②.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:∵的相反数是,
因此选.
2、【答案】C
【解析】A、,所以A不符合题意;
B、,所以B不符合题意;
C、,所以C符合题意;
D、,所以D不符合题意;
因此选:C.
3、【答案】C
【解析】
解不等式①,得,;
解不等式②,得,
所以不等式组的解集为:.
因此选:C.
4、【答案】B
【解析】
甲 乙 丙
甲 (乙,甲) (丙,甲)
乙 (甲,乙) (丙,乙)
丙 (甲,丙) (乙,丙)
由表格可知,一共有6种等可能的结果,其中甲、乙两人同时被选中的结果有2种,
所以甲、乙两人同时被选中的概率为.
因此选:B.
5、【答案】A
【解析】∵,
∴
∴,
因此选:A.
6、【答案】A
【解析】A、正方形的对角线相等且互相垂直平分,说法正确;
B、对角互补的四边形不一定是平行四边形,只是内接于圆,说法错误;
C、矩形的对角线不一定垂直,但相等,说法错误;
D、一组邻边相等的平行四边形才构成菱形,说法错误.
因此选:A.
7、【答案】C
【解析】∵四边形是正方形
∴,,
∵
∴,
∴
∴
又∵,
∴
∴
∴
∴
因此选:C.
8、【答案】C
【解析】观察表中的规律发现,分数的分子是几,则必在第几列;只有第一列的分数,分母与其所在行数一致,故在第20列,即;向前递推到第1列时,分数为,所以分数与分数在同一行.即在第2042行,即.
∴
因此选:C.
二、填空题
9、【答案】a6b3
【解析】根据积的乘方运算法则可得 (a2b)3= a6b 3.
因此答案为:a6b3
10、【答案】
【解析】解:,
因此答案为:.
11、【答案】
【解析】根据题意得:,
解得:,
因此答案为:.
12、【答案】
【解析】,
因此答案为:.
13、【答案】
【解析】解:因为关于x的方程有两个不相等的实数根,
所以,
解得.
因此答案为:.
14、【答案】8.5
【解析】张华同学掷实心球10次的成绩出现频次最高的是8.5米,共3次,故张华同学掷实心球成绩的众数是8.5.
因此答案为:8.5.
15、【答案】##0.8
【解析】∵在中,,,,
∴
∵
∴,
∴
∴
∴
∵
∴
∴
∴
∴.
因此答案为:.
16、【答案】0.1
【解析】∵,
∴,
∵C是弦的中点,D在上,,
∴延长可得O在上,
∴,
∴,
,
∴.
因此答案为:.
解答题
17、【答案】0
【解析】原式
.
18、【答案】
【解析】解:将①得:③
得:
将代入①得:
所以是原方程组的解.
解答题
19、【答案】,
【解析】解:原式
,
当时,原式
20、【答案】(1),
(2)或
【解析】解:(1)将点代入得:
解得:
将代入得:
∴
(2)由得:,解得
所以的坐标分别为
由图形可得:当或时,
五、解答题
21、【答案】(1)9.2 (2)160吨;172吨
(3)264.5吨
【解析】解:(1)(吨)
因此答案为:9.2.
(2)2018年至2022年该种粮大户粮食总产量从小到大排列如下:
120,150,160,200,230
∴2018年至2022年该种粮大户粮食总产量的中位数是160吨;
(吨)
∴2018年至2022年该种粮大户粮食总产量的平均数是172吨;
因此答案为:160吨,172吨;
(3)
(吨)
∴2023年该粮食大户的粮食总产量是264.5吨.
22、【答案】(1)A型,B型玩具的单价分别是10元/个,15元/个
(2)最多可购进A型玩具25个
【解析】解:(1)设型玩具的单价为元/件.
由题意得:,
解得:
经检验,是原方程的解
B型玩具的单价为元/个
所以A型,B型玩具的单价分别是10元/个,15元/个.
(2)设购进A型玩具个.
解得:
所以最多可购进A型玩具25个.
六、解答题
23、【答案】
【解析】解:方法一:如图所示,
过点作交的延长线于点,
四边形是平行四边形,,
,
,
过点作于点,
根据题意可知,,
,
又,
,
过作于点,
,,
,
,
靠背顶端点距地面高度为
;
方法二:
如图所示,过点作交的延长线于点,过点作于点,延长交于点,
,,
,
又,
,
,
,
过作于,
根据题意可知,,
,
又,
,
靠背顶端点距地面高度为.
24、【答案】(1)证明见解析;
(2),.
【解析】(1)证明:连接
∵为的中点,
∴,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,为半径,
∴为的切线,
(2)解:∵为直径,
∴,
∵,
∴,
又∵,,
∴,
∴,即,
∴,
∵,
∴,
在中,由勾股定理得:
.
七、解答题
25、【答案】(1)
(2)30 (3)
【解析】解:(1)∵二次函数的图象与轴交于两点.
∴设二次函数的表达式为
∵,
∴,即的坐标为
则,得
∴二次函数表达式为;
(2)
∴顶点的坐标为
过作于,作于,
四边形的面积
;
(3)如图,是抛物线上的一点,且在第一象限,当时,
连接,过点作交于点,过点作于点,
∵,则为等腰直角三角形,.
由勾股定理得:,
∵,
∴,
即,
∴
由,得,
∴.
∴是等腰直角三角形
∴
∴的坐标为
所以过的直线的解析式为
令
解得,或
所以直线与抛物线的两个交点为
即所求点的坐标为
26、【答案】(1)证明见解析
(2)①见解析,②见解析
【解析】证明:(1)∵是的中点,
∴是的垂直平分线,
又∵E在上,
∴,
在和中,
∴
(2)①如图所示,连接,
∵分别是和的中点,
∴为的中位线,
∴,
∴,
又∵,
∴,
又∵,
∴,
在和中,,
∴,
∴,
∴,
又∵,
∴;
②和中,,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
又∵A、H分别为和中点,
∴为的中位线,
∴,
∴,即为中点,
又∵,
∴为中点,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖南省常德市数学中考真题名师详解版
考生注意:
1.请考生在试题卷首填写好准考证号及姓名.
2.请将答案填写在答题卡上,填写在试题卷上的无效。
3.本学科试题卷共4页,七道大题,满分120分,考试时量120分钟.
一、选择题(本大题8个小题,每小题3分,满分24分)
1. 的相反数是( )
A. B. C. D.
2. 下面算法正确的是( )
A. B. C. D.
3. 不等式组的解集是( )
A. B. C. D.
4. 我市“神十五”航天员张陆和他的两位战友已于2023年6月4日回到地球家园,“神十六”的三位航天员已在中国空间站开始值守,空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱,假设“神十六”甲、乙、丙三名航天员从核心舱进入问天实验舱和梦天实验舱开展实验的机会均等,现在要从这三名航天员中选2人各进入一个实验舱开展科学实验,则甲、乙两人同时被选中的概率为( )
A. B. C. D.
5. 若,则( )
A. 5 B. 1 C. D. 0
6. 下列命题正确的是( )
A. 正方形的对角线相等且互相平分 B. 对角互补的四边形是平行四边形
C. 矩形的对角线互相垂直 D. 一组邻边相等的四边形是菱形
7. 如图1,在正方形中,对角线相交于点O,E,F分别为,上的一点,且,连接.若,则的度数为( )
A. B. C. D.
8. 观察下边的数表(横排为行,竖排为列),按数表中的规律,分数若排在第a行b列,则的值为( )
……
A. 2003 B. 2004 C. 2022 D. 2023
二、填空题(本大题8个小题,每小题3分,满分24分)
9. 计算:(a2b)3=___.
10. 分解因式:_______.
11. 要使二次根式有意义,则x应满足的条件是__________.
12. 联合国2022年11月15日宣布,全世界人口已达80亿.将8000000000用科学记数法表示为__________.
13. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是_________.
14. 我市体育中考有必考和选考项目,掷实心球是必考项目之一,在一次训练中,张华同学掷实心球10次成绩依次是(单位:米)7.6,8.5,8.6,8.5,9.1,8.5,8.4,8.6,9.2,73.则张华同学撰实心球成绩的众数是__________.
15. 如图1,在中,,,,D是上一点,且,过点D作交于E,将绕A点顺时针旋转到图2位置.则图2中的值为__________.
16. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上,.“会圆术”给出长l的近似值s计算公式:,当,时,__________.(结果保留一位小数)
三、(本大题2个小题,每小题5分,满分10分)
17. 计算:
18. 解方程组:
四、(本大题2个小题,每小题6分,满分12分)
19. 先化简,再求值:,其中.
20. 如图所示,一次函数与反比例函数相交于点A和点.
(1)求m的值和反比例函数解析式;
(2)当时,求x的取值范围.
五、(本大题2个小题,每小题7分,满分14分)
21. 党的二十大报告指出:“我们要全方位夯实粮食安全根基,牢牢守住十八亿亩耕地红线.确保中国人的饭碗牢牢端在自己手中”.为了了解粮食生产情况,某校数学兴趣小组调查了某种粮大户2018年至2022年粮食总产量及2022年粮食分季节占比情况如下:
请根据图中信息回答下列问题:
(1)该种粮大户2022年早稻产量是__________吨;
(2)2018年至2022年该种粮大户粮食总产量的中位数是__________,平均数是__________;
(3)该粮食大户估计2023年的粮食总产量年增长率与2022年的相同,那么2023年该粮食大户的粮食总产量是多少吨?
22. “六一”儿童节将至,张老板计划购买A型玩具和B型玩具进行销售,若用1200元购买A型玩具的数量比用1500元购买B型玩具的数量多20个,且一个B型玩具的进价是一个A型玩具进价的1.5倍.
(1)求A型玩具和B型玩具的进价分别是多少?
(2)若A型玩具售价为12元/个,B型玩具的售价为20元/个,张老板购进A,B型玩具共75个,要使总利润不低于300元,则A型玩具最多购进多少个?
六、(本大题2个小题,每小题8分,满分16分)
23. 今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且,,靠背,支架,扶手的一部分.这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:,,)
24. 如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
七、(本大题2个小题,每小题10分,满分20分)
25. 如图,二次函数的图象与x轴交于,两点,与y轴交于点C,顶点为D.O为坐标原点,.
(1)求二次函数的表达式;
(2)求四边形的面积;
(3)P是抛物线上的一点,且在第一象限内,若,求P点的坐标.
26. 如图,在中,,D是中点,延长至E,连接.
(1)求证:;
(2)在如图1中,若,其它条件不变得到图2,在图2中过点D作于F,设H是中点,过点H作交于G,交于M.
求证:
①;
②.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:∵的相反数是,
因此选.
2、【答案】C
【解析】A、,所以A不符合题意;
B、,所以B不符合题意;
C、,所以C符合题意;
D、,所以D不符合题意;
因此选:C.
3、【答案】C
【解析】
解不等式①,得,;
解不等式②,得,
所以不等式组的解集为:.
因此选:C.
4、【答案】B
【解析】
甲 乙 丙
甲 (乙,甲) (丙,甲)
乙 (甲,乙) (丙,乙)
丙 (甲,丙) (乙,丙)
由表格可知,一共有6种等可能的结果,其中甲、乙两人同时被选中的结果有2种,
所以甲、乙两人同时被选中的概率为.
因此选:B.
5、【答案】A
【解析】∵,
∴
∴,
因此选:A.
6、【答案】A
【解析】A、正方形的对角线相等且互相垂直平分,说法正确;
B、对角互补的四边形不一定是平行四边形,只是内接于圆,说法错误;
C、矩形的对角线不一定垂直,但相等,说法错误;
D、一组邻边相等的平行四边形才构成菱形,说法错误.
因此选:A.
7、【答案】C
【解析】∵四边形是正方形
∴,,
∵
∴,
∴
∴
又∵,
∴
∴
∴
∴
因此选:C.
8、【答案】C
【解析】观察表中的规律发现,分数的分子是几,则必在第几列;只有第一列的分数,分母与其所在行数一致,故在第20列,即;向前递推到第1列时,分数为,所以分数与分数在同一行.即在第2042行,即.
∴
因此选:C.
二、填空题
9、【答案】a6b3
【解析】根据积的乘方运算法则可得 (a2b)3= a6b 3.
因此答案为:a6b3
10、【答案】
【解析】解:,
因此答案为:.
11、【答案】
【解析】根据题意得:,
解得:,
因此答案为:.
12、【答案】
【解析】,
因此答案为:.
13、【答案】
【解析】解:因为关于x的方程有两个不相等的实数根,
所以,
解得.
因此答案为:.
14、【答案】8.5
【解析】张华同学掷实心球10次的成绩出现频次最高的是8.5米,共3次,故张华同学掷实心球成绩的众数是8.5.
因此答案为:8.5.
15、【答案】##0.8
【解析】∵在中,,,,
∴
∵
∴,
∴
∴
∴
∵
∴
∴
∴
∴.
因此答案为:.
16、【答案】0.1
【解析】∵,
∴,
∵C是弦的中点,D在上,,
∴延长可得O在上,
∴,
∴,
,
∴.
因此答案为:.
解答题
17、【答案】0
【解析】原式
.
18、【答案】
【解析】解:将①得:③
得:
将代入①得:
所以是原方程组的解.
解答题
19、【答案】,
【解析】解:原式
,
当时,原式
20、【答案】(1),
(2)或
【解析】解:(1)将点代入得:
解得:
将代入得:
∴
(2)由得:,解得
所以的坐标分别为
由图形可得:当或时,
五、解答题
21、【答案】(1)9.2 (2)160吨;172吨
(3)264.5吨
【解析】解:(1)(吨)
因此答案为:9.2.
(2)2018年至2022年该种粮大户粮食总产量从小到大排列如下:
120,150,160,200,230
∴2018年至2022年该种粮大户粮食总产量的中位数是160吨;
(吨)
∴2018年至2022年该种粮大户粮食总产量的平均数是172吨;
因此答案为:160吨,172吨;
(3)
(吨)
∴2023年该粮食大户的粮食总产量是264.5吨.
22、【答案】(1)A型,B型玩具的单价分别是10元/个,15元/个
(2)最多可购进A型玩具25个
【解析】解:(1)设型玩具的单价为元/件.
由题意得:,
解得:
经检验,是原方程的解
B型玩具的单价为元/个
所以A型,B型玩具的单价分别是10元/个,15元/个.
(2)设购进A型玩具个.
解得:
所以最多可购进A型玩具25个.
六、解答题
23、【答案】
【解析】解:方法一:如图所示,
过点作交的延长线于点,
四边形是平行四边形,,
,
,
过点作于点,
根据题意可知,,
,
又,
,
过作于点,
,,
,
,
靠背顶端点距地面高度为
;
方法二:
如图所示,过点作交的延长线于点,过点作于点,延长交于点,
,,
,
又,
,
,
,
过作于,
根据题意可知,,
,
又,
,
靠背顶端点距地面高度为.
24、【答案】(1)证明见解析;
(2),.
【解析】(1)证明:连接
∵为的中点,
∴,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,为半径,
∴为的切线,
(2)解:∵为直径,
∴,
∵,
∴,
又∵,,
∴,
∴,即,
∴,
∵,
∴,
在中,由勾股定理得:
.
七、解答题
25、【答案】(1)
(2)30 (3)
【解析】解:(1)∵二次函数的图象与轴交于两点.
∴设二次函数的表达式为
∵,
∴,即的坐标为
则,得
∴二次函数表达式为;
(2)
∴顶点的坐标为
过作于,作于,
四边形的面积
;
(3)如图,是抛物线上的一点,且在第一象限,当时,
连接,过点作交于点,过点作于点,
∵,则为等腰直角三角形,.
由勾股定理得:,
∵,
∴,
即,
∴
由,得,
∴.
∴是等腰直角三角形
∴
∴的坐标为
所以过的直线的解析式为
令
解得,或
所以直线与抛物线的两个交点为
即所求点的坐标为
26、【答案】(1)证明见解析
(2)①见解析,②见解析
【解析】证明:(1)∵是的中点,
∴是的垂直平分线,
又∵E在上,
∴,
在和中,
∴
(2)①如图所示,连接,
∵分别是和的中点,
∴为的中位线,
∴,
∴,
又∵,
∴,
又∵,
∴,
在和中,,
∴,
∴,
∴,
又∵,
∴;
②和中,,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
又∵A、H分别为和中点,
∴为的中位线,
∴,
∴,即为中点,
又∵,
∴为中点,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
