2023年湖南省郴州市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖南省郴州市数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年湖南省郴州市数学中考真题名师详解版
注意事项:
1.答题前,考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上,并认真填涂和核对答题卡上的姓名、准考证号和科目;
2.选择题部分请按题号用2B铅笔填涂方框,修改时用橡皮擦擦干净,不留痕迹;
3.非选择题部分请按题号用0.5毫米黑色签字笔书写,否则作答无效;
4.在草稿纸、试题卷上答题无效;
5.请勿折叠答题卡,保证字体工整、笔迹清晰、卡面清洁;
6.答题完成后,请将试题卷、答题卡放在桌上,由监考老师统一收回.
本试卷共8页,有三道大题,共26小题,满分130分,考试时间120分钟.
一、选择题(共8小题,每小题3分,共24分)
1. 的倒数是( )
A. 2 B. C. D.
2. 下列图形中,能由图形通过平移得到的是( )
A B. C. D.
3. 下列运算正确的是( )
A. B. C. D.
4. 下列几何体中,各自的三视图完全一样的是( )
A. B. C. D.
5. 下列问题适合全面调查的是( )
A. 调查市场上某品牌灯泡的使用寿命
B. 了解全市人民对湖南省第二届旅发大会的关注情况
C. 了解郴江河的水质情况
D. 神舟十六号飞船发射前对飞船仪器设备的检查
6. 一元一次不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
7. 小王从A地开车去B地,两地相距240km.原计划平均速度为km/h,实际平均速度提高了50%,结果提前1小时到达.由此可建立方程为( )
A. B. C. D.
8. 第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离与时间的函数图象.分析图中信息,下列说法正确的是( )
A. 途中修车花了
B. 修车之前的平均速度是/
C. 车修好后的平均速度是/
D. 车修好后的平均速度是修车之前的平均速度的倍
二、填空题(共8小题,每小题3分,共24分)
9. 计算:___.
10. 在一次函数中,随的增大而增大,则的值可以是___________(任写一个符合条件的数即可).
11. 在一个不透明的袋子中装有3个白球和7个红球,它们除颜色外,大小、质地都相同.从袋子中随机取出一个球,是红球的概率是___________.
12 抛物线与轴只有一个交点,则________.
13. 为积极响应“助力旅发大会,唱响美丽郴州”号召,某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评.某参赛队歌曲内容获得90分,演唱技巧获得94分,精神面貌获得95分.则该参赛队的最终成绩是___________分.
14. 在 Rt △ABC中, ∠ACB=90°,AC=6,BC=8,D是AB的中点,则 _______.
15. 如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是,为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器___________台.
16. 如图,在中,,,.将绕点逆时针旋转,得到,若点的对应点恰好落在线段上,则点的运动路径长是___________cm(结果用含的式子表示).
三、解答题(17~19题每题6分,20~23题每题8分,24~25题每题10分,26题12分,共82分)
17. 计算:.
18. 先化简,再求值:,其中.
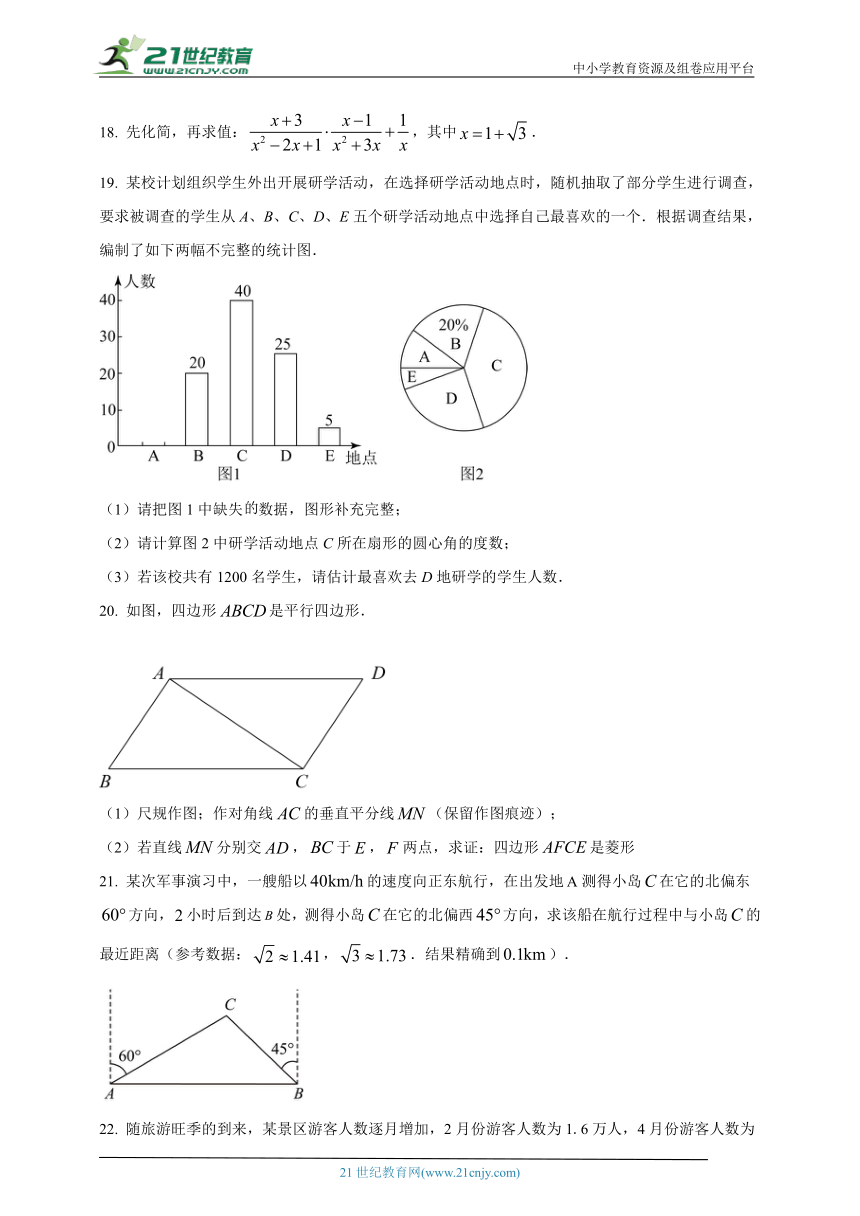
19. 某校计划组织学生外出开展研学活动,在选择研学活动地点时,随机抽取了部分学生进行调查,要求被调查的学生从A、B、C、D、E五个研学活动地点中选择自己最喜欢的一个.根据调查结果,编制了如下两幅不完整的统计图.
(1)请把图1中缺失数据,图形补充完整;
(2)请计算图2中研学活动地点C所在扇形的圆心角的度数;
(3)若该校共有1200名学生,请估计最喜欢去D地研学的学生人数.
20. 如图,四边形是平行四边形.
(1)尺规作图;作对角线的垂直平分线(保留作图痕迹);
(2)若直线分别交,于,两点,求证:四边形是菱形
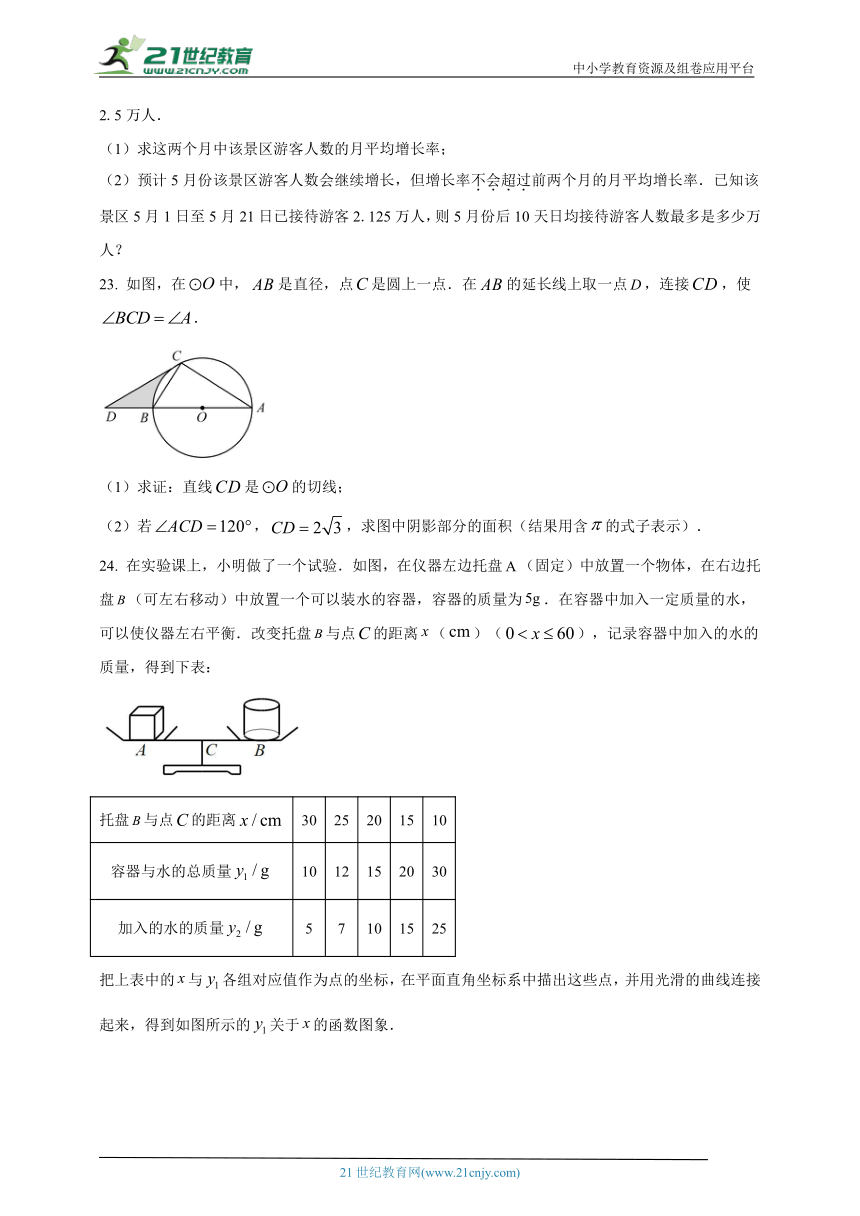
21. 某次军事演习中,一艘船以的速度向正东航行,在出发地测得小岛在它的北偏东方向,小时后到达处,测得小岛在它的北偏西方向,求该船在航行过程中与小岛的最近距离(参考数据:,.结果精确到).
22. 随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.
(1)求这两个月中该景区游客人数的月平均增长率;
(2)预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?
23. 如图,在中,是直径,点是圆上一点.在的延长线上取一点,连接,使.
(1)求证:直线是的切线;
(2)若,,求图中阴影部分的面积(结果用含的式子表示).
24. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为.在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
托盘与点的距离 30 25 20 15 10
容器与水的总质量 10 12 15 20 30
加入的水的质量 5 7 10 15 25
把上表中的与各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的关于的函数图象.
(1)请在该平面直角坐标系中作出关于的函数图象;
(2)观察函数图象,并结合表中的数据:
①猜测与之间的函数关系,并求关于的函数表达式;
②求关于的函数表达式;
③当时,随的增大而___________(填“增大”或“减小”),随的增大而___________(填“增大”或“减小”),的图象可以由的图象向___________(以“上”或“下”或“左”或“右”)平移得到.
(3)若在容器中加入的水的质量(g)满足,求托盘与点的距离(cm)的取值范围.
25. 已知是等边三角形,点是射线上的一个动点,延长至点,使,连接交射线于点.
(1)如图1,当点在线段上时,猜测线段与的数量关系并说明理由;
(2)如图2,当点在线段的延长线上时,
①线段与的数量关系是否仍然成立?请说明理由;
②如图3,连接.设,若,求四边形的面积.
26. 已知抛物线与轴相交于点,,与轴相交于点.
(1)求抛物线的表达式;
(2)如图1,点是抛物线对称轴上的一个动点,当的周长最小时,求的值;
(3)如图2,取线段的中点,在抛物线上是否存在点,使?若存在,求出点的坐标;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:因为
所以-2的倒数为
因此选:B.
2、【答案】B
【解析】解:观察图形可知,B中图形能由图形通过平移得到,A,C,D均不能由图形通过平移得到;
因此选:B.
3、【答案】A
【解析】解:A、,此项计算正确,符合题意;
B、,此项计算错误,不符合题意;
C、,此项计算错误,不符合题意;
D、,此项计算错误,不符合题意;
因此选:A.
4、【答案】D
【解析】A、直三棱柱的俯视图为三角形,与主视图长方形和左视图长方形均不同,所以A错误;
B、圆锥的俯视图为圆,与主视图三角形和左视图三角形均不同,所以B错误;
C、圆柱的俯视图为圆,与主视图长方形和左视图长方形均不同,所以C错误;
D、球的三视图完全相同,都是圆,所以D正确;
因此选:D.
5、【答案】D
【解析】解:由题意知,A、B、C项数量较大,也不需要非常精确的数据,适于抽查,所以不符合要求;
D项关乎生命安全且需要的数据比较精确,适于全面调查,所以符合要求;
因此选:D.
6、【答案】C
【解析】解:由,得:;
由,得:,
所以不等式组的解集为:;
在数轴上表示如图:
因此选:C.
7、【答案】B
【解析】解:设原计划平均速度为km/h,由题意得:
,即:;
因此选:B
8、【答案】D
【解析】解:由图象可知途中修车花了,
修车之前的平均速度是÷/,
车修好后的平均速度是÷/,
所以
所以A、B、C错误,D正确.
因此选∶ D.
填空题
9、【答案】3
【解析】解: ∵33=27,
∴.
因此答案3.
10、【答案】3(答案不唯一)
【解析】解:因为一次函数中,y随x的值增大而增大,
所以.
解得:,
因此答案为:3(答案不唯一).
11、【答案】##0.7
【解析】解:由题意得,随机取出一个球共有10种等可能的结果,其中取出的是红球共有7种等可能的结果,
所以;
因此答案为:.
12、【答案】9
【解析】解:因为抛物线与轴只有一个交点,
所以
解得,c=9.
因此答案为:9.
13、【答案】93
【解析】解:由题意,得:(分);
所以该参赛队的最终成绩是93分,
因此答案为:93
14、【答案】5
【解析】解:如图:∵AC=6,BC=8,∠ACB=90°,
∴
∵∠ACB=90°,D为AB的中点,
∴CD=AB=×10=5.
因此答案为5.
15、【答案】4
【解析】解:∵,
∴对应的圆心角的度数为,
,
∴最少需要在圆形边缘上共安装这样的监视器台.
因此答案为:4
16、【答案】
【解析】如图,以A为圆心作圆弧,
在直角中,,则,
则.
∴.
由旋转性质可知,,又,
∴是等边三角形.
∴.
由旋转性质知,.
所以弧的长度为:;
因此答案为:
解答题
17、【答案】4
【解析】解:原式
.
18、【答案】,
【解析】解:
,
当时,原式.
19、【答案】(1)见解析;
(2);
(3)300.
【解析】解:(1)(人)
选择的人数:(人)
补全图形如下:
(2),
∴研学活动地点所在扇形的圆心角的度数;
(3)(人)
答:最喜欢去地研学的学生人数共有人.
20、【答案】(1)见解析 (2)见解析
【解析】(1)解:如图所示,即为所求;
(2)证明:∵四边形是平行四边形,
∴,
∴,
如图所示,设与交于点,
∵是的垂直平分线,
∴,,
∵,
∴,
∴,
∴四边形为平行四边形,
∵,
∴四边形为菱形.
21、【答案】该船在航行过程中与小岛的最近距离.
【解析】解:如图所示,过点作,垂足为点,
解∶∵,,,,,
∴,,,
在中,,即,
∴,
在中,,即,
∴,
∴,
∴(),
∴该船在航行过程中与小岛的最近距离.
22、【答案】(1)这两个月中该景区游客人数的月平均增长率为
(2)5月份后10天日均接待游客人数最多是1万人
【解析】解:(1)设这两个月中该景区游客人数的月平均增长率为,由题意,得:
,
解得:(负值已舍掉);
答:这两个月中该景区游客人数的月平均增长率为;
(2)设5月份后10天日均接待游客人数是y万人,由题意得:
,
解得:;
即5月份后10天日均接待游客人数最多是1万人.
23、【答案】(1)见解析;
(2).
【解析】(1)证明:连接,
∵是直径,
∴,
∵,,
∴,
∴,
∴,
∵是的半径,
∴直线是的切线;
(2)解:∵,,
∴,
∴,
∵在中,,,
∴,解得,
∴.
24、【答案】(1)作图见解析;
(2)①;②;③减小,减小,下;
(3).
【解析】解∶(1)函数图象如图所示,
(2)①观察图象可知,可能是反比例函数,设,
把的坐标代入,得,
经检验,其余各个点坐标均满足,
所以关于的函数表达式;
②观察表格以及①可知,可能与成反比例,设,
把的坐标代入,得,
经检验,其余各个点坐标均满足,
所以关于的函数表达式;
③由图象可知,当时,随的增大而减小,随的增大而减小,的图象可以由的图象向下平移得到,
因此答案为:减小,减小,下;
(3)当时,解得,
当时,解得,
所以托盘与点的距离()的取值范围.
25、【答案】(1),理由见解析
(2)①成立,理由见解析②
【解析】解:(1),理由如下:
∵是等边三角形,
∴,
过点作,交于点,
∴,,
∴为等边三角形,
∴,
∵,,
∴,,
又,
∴,
∴,
∴;
(2)①成立,理由如下:
∵是等边三角形,
∴,
过点作,交的延长线于点,如图所示,
∴,,
∴为等边三角形,
∴,
∵,,
∴,,
又,
∴,
∴,
∴;
②如图所示,过点作,交的延长线于点,过点作,交于点,交于点,则:,
由①知:为等边三角形,,,
∵为等边三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
设,则:,,
∴,
∵,
∴,
∴,即:②,
联立①②可得:(负值已舍去),
经检验,是原方程根,
∴,,,
∴,
∴,
∵,
∴,
∴四边形的面积为
.
26、【答案】(1)
(2)
(3)或或或
【解析】解:(1)∵抛物线与轴相交于点,,
∴,解得:,
∴抛物线的表达式为;
(2)∵,当时,,
∴,抛物线的对称轴为直线
∵的周长等于,为定长,
∴当的值最小时,的周长最小,
∵关于对称轴对称,
∴,当三点共线时,的值最小,为的长,此时点为直线与对称轴的交点,
设直线的解析式为:,
则:,解得:,
∴,
当时,,
∴,
∵,
∴,,
∴;
(3)存在,
∵为的中点,
∴,
∴,
∵,
∴,
在中,,
∵,
∴,
①当点在点上方时:
过点作,交抛物线与点,则:,此时点纵坐标为2,
设点横坐标,
则:,
解得:,
∴或;
②当点在点下方时:设与轴交于点,
则:,
设,
则:,,
∴,解得:,
∴,
设的解析式为:,
则:,解得:,
∴,
联立,解得:或,
∴或;
综上所述:或或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖南省郴州市数学中考真题名师详解版
注意事项:
1.答题前,考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上,并认真填涂和核对答题卡上的姓名、准考证号和科目;
2.选择题部分请按题号用2B铅笔填涂方框,修改时用橡皮擦擦干净,不留痕迹;
3.非选择题部分请按题号用0.5毫米黑色签字笔书写,否则作答无效;
4.在草稿纸、试题卷上答题无效;
5.请勿折叠答题卡,保证字体工整、笔迹清晰、卡面清洁;
6.答题完成后,请将试题卷、答题卡放在桌上,由监考老师统一收回.
本试卷共8页,有三道大题,共26小题,满分130分,考试时间120分钟.
一、选择题(共8小题,每小题3分,共24分)
1. 的倒数是( )
A. 2 B. C. D.
2. 下列图形中,能由图形通过平移得到的是( )
A B. C. D.
3. 下列运算正确的是( )
A. B. C. D.
4. 下列几何体中,各自的三视图完全一样的是( )
A. B. C. D.
5. 下列问题适合全面调查的是( )
A. 调查市场上某品牌灯泡的使用寿命
B. 了解全市人民对湖南省第二届旅发大会的关注情况
C. 了解郴江河的水质情况
D. 神舟十六号飞船发射前对飞船仪器设备的检查
6. 一元一次不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
7. 小王从A地开车去B地,两地相距240km.原计划平均速度为km/h,实际平均速度提高了50%,结果提前1小时到达.由此可建立方程为( )
A. B. C. D.
8. 第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离与时间的函数图象.分析图中信息,下列说法正确的是( )
A. 途中修车花了
B. 修车之前的平均速度是/
C. 车修好后的平均速度是/
D. 车修好后的平均速度是修车之前的平均速度的倍
二、填空题(共8小题,每小题3分,共24分)
9. 计算:___.
10. 在一次函数中,随的增大而增大,则的值可以是___________(任写一个符合条件的数即可).
11. 在一个不透明的袋子中装有3个白球和7个红球,它们除颜色外,大小、质地都相同.从袋子中随机取出一个球,是红球的概率是___________.
12 抛物线与轴只有一个交点,则________.
13. 为积极响应“助力旅发大会,唱响美丽郴州”号召,某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评.某参赛队歌曲内容获得90分,演唱技巧获得94分,精神面貌获得95分.则该参赛队的最终成绩是___________分.
14. 在 Rt △ABC中, ∠ACB=90°,AC=6,BC=8,D是AB的中点,则 _______.
15. 如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是,为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器___________台.
16. 如图,在中,,,.将绕点逆时针旋转,得到,若点的对应点恰好落在线段上,则点的运动路径长是___________cm(结果用含的式子表示).
三、解答题(17~19题每题6分,20~23题每题8分,24~25题每题10分,26题12分,共82分)
17. 计算:.
18. 先化简,再求值:,其中.
19. 某校计划组织学生外出开展研学活动,在选择研学活动地点时,随机抽取了部分学生进行调查,要求被调查的学生从A、B、C、D、E五个研学活动地点中选择自己最喜欢的一个.根据调查结果,编制了如下两幅不完整的统计图.
(1)请把图1中缺失数据,图形补充完整;
(2)请计算图2中研学活动地点C所在扇形的圆心角的度数;
(3)若该校共有1200名学生,请估计最喜欢去D地研学的学生人数.
20. 如图,四边形是平行四边形.
(1)尺规作图;作对角线的垂直平分线(保留作图痕迹);
(2)若直线分别交,于,两点,求证:四边形是菱形
21. 某次军事演习中,一艘船以的速度向正东航行,在出发地测得小岛在它的北偏东方向,小时后到达处,测得小岛在它的北偏西方向,求该船在航行过程中与小岛的最近距离(参考数据:,.结果精确到).
22. 随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.
(1)求这两个月中该景区游客人数的月平均增长率;
(2)预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?
23. 如图,在中,是直径,点是圆上一点.在的延长线上取一点,连接,使.
(1)求证:直线是的切线;
(2)若,,求图中阴影部分的面积(结果用含的式子表示).
24. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为.在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
托盘与点的距离 30 25 20 15 10
容器与水的总质量 10 12 15 20 30
加入的水的质量 5 7 10 15 25
把上表中的与各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的关于的函数图象.
(1)请在该平面直角坐标系中作出关于的函数图象;
(2)观察函数图象,并结合表中的数据:
①猜测与之间的函数关系,并求关于的函数表达式;
②求关于的函数表达式;
③当时,随的增大而___________(填“增大”或“减小”),随的增大而___________(填“增大”或“减小”),的图象可以由的图象向___________(以“上”或“下”或“左”或“右”)平移得到.
(3)若在容器中加入的水的质量(g)满足,求托盘与点的距离(cm)的取值范围.
25. 已知是等边三角形,点是射线上的一个动点,延长至点,使,连接交射线于点.
(1)如图1,当点在线段上时,猜测线段与的数量关系并说明理由;
(2)如图2,当点在线段的延长线上时,
①线段与的数量关系是否仍然成立?请说明理由;
②如图3,连接.设,若,求四边形的面积.
26. 已知抛物线与轴相交于点,,与轴相交于点.
(1)求抛物线的表达式;
(2)如图1,点是抛物线对称轴上的一个动点,当的周长最小时,求的值;
(3)如图2,取线段的中点,在抛物线上是否存在点,使?若存在,求出点的坐标;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:因为
所以-2的倒数为
因此选:B.
2、【答案】B
【解析】解:观察图形可知,B中图形能由图形通过平移得到,A,C,D均不能由图形通过平移得到;
因此选:B.
3、【答案】A
【解析】解:A、,此项计算正确,符合题意;
B、,此项计算错误,不符合题意;
C、,此项计算错误,不符合题意;
D、,此项计算错误,不符合题意;
因此选:A.
4、【答案】D
【解析】A、直三棱柱的俯视图为三角形,与主视图长方形和左视图长方形均不同,所以A错误;
B、圆锥的俯视图为圆,与主视图三角形和左视图三角形均不同,所以B错误;
C、圆柱的俯视图为圆,与主视图长方形和左视图长方形均不同,所以C错误;
D、球的三视图完全相同,都是圆,所以D正确;
因此选:D.
5、【答案】D
【解析】解:由题意知,A、B、C项数量较大,也不需要非常精确的数据,适于抽查,所以不符合要求;
D项关乎生命安全且需要的数据比较精确,适于全面调查,所以符合要求;
因此选:D.
6、【答案】C
【解析】解:由,得:;
由,得:,
所以不等式组的解集为:;
在数轴上表示如图:
因此选:C.
7、【答案】B
【解析】解:设原计划平均速度为km/h,由题意得:
,即:;
因此选:B
8、【答案】D
【解析】解:由图象可知途中修车花了,
修车之前的平均速度是÷/,
车修好后的平均速度是÷/,
所以
所以A、B、C错误,D正确.
因此选∶ D.
填空题
9、【答案】3
【解析】解: ∵33=27,
∴.
因此答案3.
10、【答案】3(答案不唯一)
【解析】解:因为一次函数中,y随x的值增大而增大,
所以.
解得:,
因此答案为:3(答案不唯一).
11、【答案】##0.7
【解析】解:由题意得,随机取出一个球共有10种等可能的结果,其中取出的是红球共有7种等可能的结果,
所以;
因此答案为:.
12、【答案】9
【解析】解:因为抛物线与轴只有一个交点,
所以
解得,c=9.
因此答案为:9.
13、【答案】93
【解析】解:由题意,得:(分);
所以该参赛队的最终成绩是93分,
因此答案为:93
14、【答案】5
【解析】解:如图:∵AC=6,BC=8,∠ACB=90°,
∴
∵∠ACB=90°,D为AB的中点,
∴CD=AB=×10=5.
因此答案为5.
15、【答案】4
【解析】解:∵,
∴对应的圆心角的度数为,
,
∴最少需要在圆形边缘上共安装这样的监视器台.
因此答案为:4
16、【答案】
【解析】如图,以A为圆心作圆弧,
在直角中,,则,
则.
∴.
由旋转性质可知,,又,
∴是等边三角形.
∴.
由旋转性质知,.
所以弧的长度为:;
因此答案为:
解答题
17、【答案】4
【解析】解:原式
.
18、【答案】,
【解析】解:
,
当时,原式.
19、【答案】(1)见解析;
(2);
(3)300.
【解析】解:(1)(人)
选择的人数:(人)
补全图形如下:
(2),
∴研学活动地点所在扇形的圆心角的度数;
(3)(人)
答:最喜欢去地研学的学生人数共有人.
20、【答案】(1)见解析 (2)见解析
【解析】(1)解:如图所示,即为所求;
(2)证明:∵四边形是平行四边形,
∴,
∴,
如图所示,设与交于点,
∵是的垂直平分线,
∴,,
∵,
∴,
∴,
∴四边形为平行四边形,
∵,
∴四边形为菱形.
21、【答案】该船在航行过程中与小岛的最近距离.
【解析】解:如图所示,过点作,垂足为点,
解∶∵,,,,,
∴,,,
在中,,即,
∴,
在中,,即,
∴,
∴,
∴(),
∴该船在航行过程中与小岛的最近距离.
22、【答案】(1)这两个月中该景区游客人数的月平均增长率为
(2)5月份后10天日均接待游客人数最多是1万人
【解析】解:(1)设这两个月中该景区游客人数的月平均增长率为,由题意,得:
,
解得:(负值已舍掉);
答:这两个月中该景区游客人数的月平均增长率为;
(2)设5月份后10天日均接待游客人数是y万人,由题意得:
,
解得:;
即5月份后10天日均接待游客人数最多是1万人.
23、【答案】(1)见解析;
(2).
【解析】(1)证明:连接,
∵是直径,
∴,
∵,,
∴,
∴,
∴,
∵是的半径,
∴直线是的切线;
(2)解:∵,,
∴,
∴,
∵在中,,,
∴,解得,
∴.
24、【答案】(1)作图见解析;
(2)①;②;③减小,减小,下;
(3).
【解析】解∶(1)函数图象如图所示,
(2)①观察图象可知,可能是反比例函数,设,
把的坐标代入,得,
经检验,其余各个点坐标均满足,
所以关于的函数表达式;
②观察表格以及①可知,可能与成反比例,设,
把的坐标代入,得,
经检验,其余各个点坐标均满足,
所以关于的函数表达式;
③由图象可知,当时,随的增大而减小,随的增大而减小,的图象可以由的图象向下平移得到,
因此答案为:减小,减小,下;
(3)当时,解得,
当时,解得,
所以托盘与点的距离()的取值范围.
25、【答案】(1),理由见解析
(2)①成立,理由见解析②
【解析】解:(1),理由如下:
∵是等边三角形,
∴,
过点作,交于点,
∴,,
∴为等边三角形,
∴,
∵,,
∴,,
又,
∴,
∴,
∴;
(2)①成立,理由如下:
∵是等边三角形,
∴,
过点作,交的延长线于点,如图所示,
∴,,
∴为等边三角形,
∴,
∵,,
∴,,
又,
∴,
∴,
∴;
②如图所示,过点作,交的延长线于点,过点作,交于点,交于点,则:,
由①知:为等边三角形,,,
∵为等边三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
设,则:,,
∴,
∵,
∴,
∴,即:②,
联立①②可得:(负值已舍去),
经检验,是原方程根,
∴,,,
∴,
∴,
∵,
∴,
∴四边形的面积为
.
26、【答案】(1)
(2)
(3)或或或
【解析】解:(1)∵抛物线与轴相交于点,,
∴,解得:,
∴抛物线的表达式为;
(2)∵,当时,,
∴,抛物线的对称轴为直线
∵的周长等于,为定长,
∴当的值最小时,的周长最小,
∵关于对称轴对称,
∴,当三点共线时,的值最小,为的长,此时点为直线与对称轴的交点,
设直线的解析式为:,
则:,解得:,
∴,
当时,,
∴,
∵,
∴,,
∴;
(3)存在,
∵为的中点,
∴,
∴,
∵,
∴,
在中,,
∵,
∴,
①当点在点上方时:
过点作,交抛物线与点,则:,此时点纵坐标为2,
设点横坐标,
则:,
解得:,
∴或;
②当点在点下方时:设与轴交于点,
则:,
设,
则:,,
∴,解得:,
∴,
设的解析式为:,
则:,解得:,
∴,
联立,解得:或,
∴或;
综上所述:或或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
