2023年湖南省衡阳市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖南省衡阳市数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023年湖南省衡阳市数学中考真题名师详解版
一、选择题(本大题共12个小题,每小题3分,满分36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 中国是最早采用正负数表示相反意义量、并进行负数运算的国家.若收入500元记作元,则支出237元记作( )
A. 元 B. 元 C. 0元 D. 元
2. 下列长度的各组线段能组成一个三角形的是( )
A. B.
C. D.
3. 下面四种化学仪器的示意图是轴对称图形的是( )
A. B. C. D.
4. 作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从左面看到的图形的是( )
A. B. C. D.
5. 计算的结果正确的是( )
A. B. C. D.
6. 据共青团中央2023年5月3日发布的中国共青团团内统计公报,截至2022年12月底,全国共有共青团员7358万.数据7358万用科学记数法表示为( )
A. B. C. D.
7. 对于二次根式的乘法运算,一般地,有.该运算法则成立的条件是( )
A. B. C. D.
8. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )
A. AB=CD B. AB∥CD C. ∠A=∠C D. BC=AD
9. 《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设有x只鸡,y只兔.依题意,可列方程组为( )
A. B.
C. D.
10. 某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如下表.甲、乙两名选手成绩的方差分别记为和,则与的大小关系是( )
测试次数 1 2 3 4 5
甲 5 10 9 3 8
乙 8 6 8 6 7
A. B. C. D. 无法确定
11. 我们可以用以下推理来证明“在一个三角形中,至少有一个内角小于或等于”.假设三角形没有一个内角小于或等于,即三个内角都大于.则三角形的三个内角的和大于,这与“三角形的内角和等于”这个定理矛盾.所以在一个三角形中,至少有一个内角小于或等于.上述推理使用的证明方法是( )
A. 反证法 B. 比较法 C. 综合法 D. 分析法
12. 已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A. B. C. D.
二、填空题(本大题共6个小题,每小题3分,满分18分.)
13. 在平面直角坐标系中,点所在象限是第________象限.
14. 一个布袋中放着3个红球和9个黑球,这两种球除了颜色以外没有任何其他区别.布袋中的球已经搅匀.从布袋中任取1个球,取出红球的概率是________.
15. 已知,则代数式的值为________.
16. 已知关于x的方程的一个根是,则它的另一个根是________.
17. 如图,在中,.以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为________.
18. 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是________ 个.
三、解答题(本大题共8个小题,19~20题每题6分,21~24题每题8分,25题10分,26题12分,满分66分.解答应写出文字说明、证明过程或演算步骤.)
19. 计算:
20. 解不等式组:
21. 2023年3月27日是第28个全国中小学生安全教育日,为提高学生安全防范意识和自我防护能力,某学校举行了校园安全知识竞赛活动.现从八、九年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,80分及以上为优秀,共分成四组,A:;B:;C:;D:),并给出下面部分信息:
八年级抽取的学生竞赛成绩在C组中的数据为:84,84,88.
九年级抽取的学生竞赛成绩为:68,77,75,100,80,100,82,86,95,91,100,86,84,94,87.
八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 优秀率
八 87 a 98
九 87 86 b c
根据以上信息,解答下列问题:
(1)填空:________,________,________.
(2)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数.
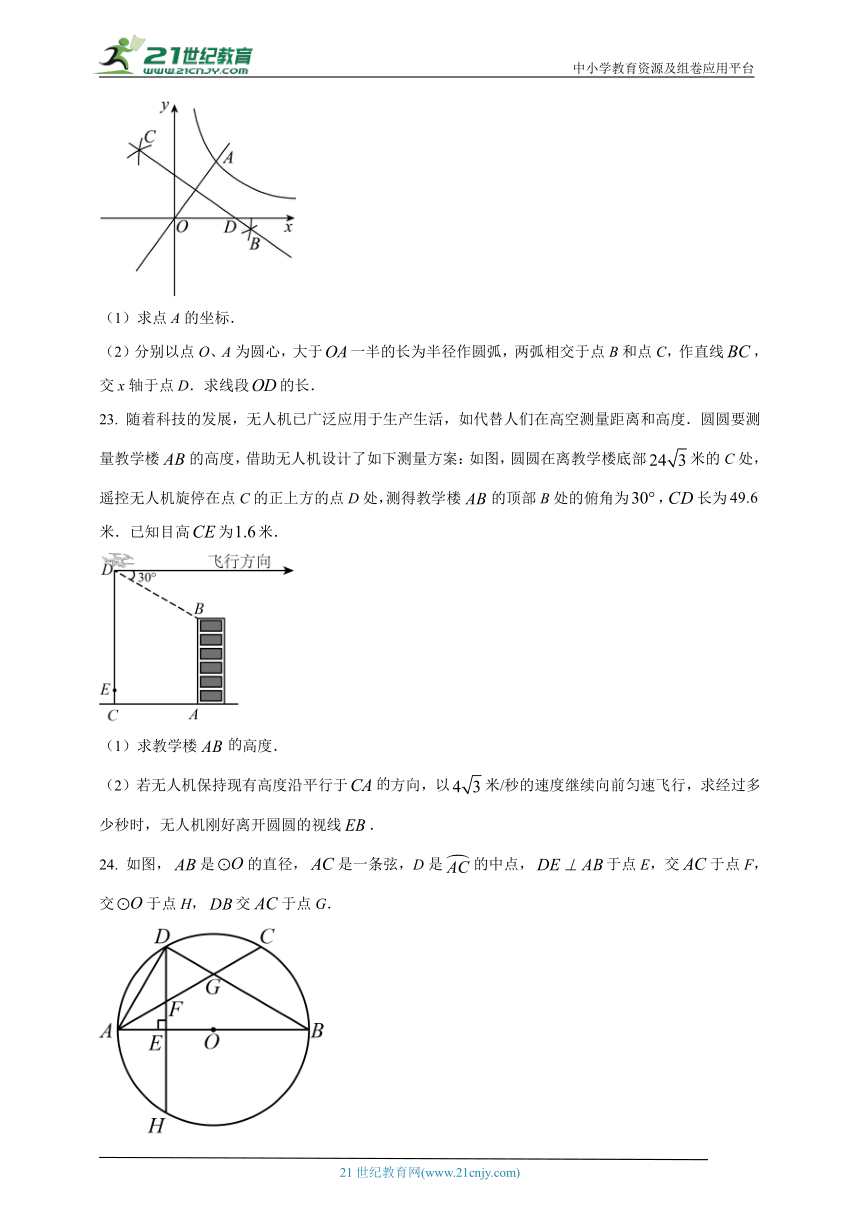
22. 如图,正比例函数的图象与反比例函数的图象相交于点A.
(1)求点A的坐标.
(2)分别以点O、A为圆心,大于一半的长为半径作圆弧,两弧相交于点B和点C,作直线,交x轴于点D.求线段的长.
23. 随着科技的发展,无人机已广泛应用于生产生活,如代替人们在高空测量距离和高度.圆圆要测量教学楼的高度,借助无人机设计了如下测量方案:如图,圆圆在离教学楼底部米的C处,遥控无人机旋停在点C的正上方的点D处,测得教学楼的顶部B处的俯角为,长为米.已知目高为米.
(1)求教学楼高度.
(2)若无人机保持现有高度沿平行于方向,以米/秒的速度继续向前匀速飞行,求经过多少秒时,无人机刚好离开圆圆的视线.
24. 如图,是的直径,是一条弦,D是的中点,于点E,交于点F,交于点H,交于点G.
(1)求证:.
(2)若,求半径.
25. (1)[问题探究]
如图1,正方形中,对角线相交于点O.在线段上任取一点P(端点除外),连接.
①求证:;
②将线段绕点P逆时针旋转,使点D落在的延长线上的点Q处.当点P在线段上的位置发生变化时,的大小是否发生变化?请说明理由;
③探究与的数量关系,并说明理由.
(2)[迁移探究]
如图2,将正方形换成菱形,且,其他条件不变.试探究与的数量关系,并说明理由.
26. 如图,已知抛物线与x轴交于点和点B,与y轴交于点C,连接,过B、C两点作直线.
(1)求a的值.
(2)将直线向下平移个单位长度,交抛物线于、两点.在直线上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线的距离最大,若存在,请求出点D的坐标;若不存在,请说明理由.
(3)抛物线上是否存在点P,使,若存在,请求出直线的解析式;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】因为收入500元记作元,
所以支出237元记作元,
因此选B.
2、【答案】D
【解析】A.,此项不符合题意;
B.,此项不符合题意;
C.,此项不符合题意;
D.,此项符合题意,
因此选D.
3、【答案】C
【解析】解:A.不是轴对称图形,本选项不合题意;
B.不是轴对称图形,本选项不符合题意;
C.是轴对称图形,本选项合题意;
D.不是轴对称图形,本选项不合题意.
因此选:C.
4、【答案】B
【解析】A. 是从上向下看得到的图形为俯视图,故A项不合题意;
B. 是从左向右看得到的图形为左视图,故B项符合题意;
C. 是从下往上看得到的图形是仰视图,故C项不合题意;
D. 是从前往后看得到的图形是主视图,故D项不合题意.
因此选B.
5、【答案】B
【解析】解:,
因此选:B.
6、【答案】A
【解析】7358万,
因此选:A.
7、【答案】D
【解析】解:根据二次根式有意义的条件,得,
,
因此选:D.
8、【答案】A
【解析】解:A、当BC∥AD,AB=CD时,不能判定四边形ABCD是平行四边形,所以此选项符合题意;
B、当AB∥CD,BC∥AD时,依据两组对边分别平行的四边形是平行四边形,能判定四边形ABCD是平行四边形,所以此选项不合题意;
C、当BC∥AD,∠A=∠C时,可推出AB∥DC,依据两组对边分别平行的四边形是平行四边形,能判定四边形ABCD是平行四边形,所以此选项不合题意;
D、当BC∥AD,BC=AD时,依据一组对边平行且相等的四边形是平行四边形,能判定四边形ABCD是平行四边形,所以此选项不合题意;
因此选:A.
9、【答案】C
【解析】解:设有x只鸡,y只兔,
根据题意得:,
因此选:C.
10、【答案】A
【解析】解:甲的平均数为,
甲的方差为,
乙的平均数为,
乙的方差为,
因为,
所以.
因此选:A.
11、【答案】A
【解析】解:假设三角形没有一个内角小于或等于,即三个内角都大于.
则三角形的三个内角的和大于,
这与“三角形的内角和等于”这个定理矛盾.
所以在一个三角形中,至少有一个内角小于或等于.
以上步骤符合反证法的步骤.
所以推理使用的证明方法是反证法.
因此选:A.
12、【答案】B
【解析】解:如图,设直线与抛物线交于A、B两点,直线与抛物线交于C、D两点,
∵,关于x的方程的解为,关于x的方程的解为,
∴分别是A、B、C、D的横坐标,
∴,
因此选B.
填空题
13、【答案】三
【解析】解:的横坐标为负数,纵坐标为负数,
在第三象限,
因此答案为:三.
14、【答案】##0.25
【解析】因为一个布袋中放着3个红球和9个黑球,
所以取出红球的概率是,
因此答案为:.
15、【答案】
【解析】解:原式=
因此答案为:
16、【答案】5
【解析】解:由题意可得:,
∴,
∵该方程一个根为,令,
∴,解得:.
因此答案:5.
17、【答案】
【解析】因为,
所以,
根据切线的性质,得到圆的半径等于边上的高,
因为,
所以,
因此答案:.
18、【答案】10
【解析】解:由题意得:
∵正五边形的一个外角,
∴,
∴,
∴共需要正五边形的个数(个),
因此答案为:10.
解答题
19、【答案】
【解析】解:
20、【答案】
【解析】解:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
21、【答案】(1)84,100,;
(2)200人
【解析】解:(1)∵一共抽取八年级学生15人,
∴中位数是排序后的第8个数据,
∵1+5=6,
∴第8个数据落在C组,
∴a第八名学生成绩,即;
∵抽取的九年级学生竞赛成绩中,100分出现了3次,出现次数最多,
∴,
∵抽取的九年级学生竞赛成绩中,80分及以上的有12个,
∴;
因此答案为:84,100,;
(2)由频数分布直方图可知,抽取的八年级学生竞赛成绩中,90分以上的有6个;
根据抽取的九年级学生的竞赛成绩可得,90分以上的有6个;
所以该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数为:(人),
答:该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数为200人.
22、【答案】(1)
(2)
【解析】解:(1)解方程组,得,
∵,
∴;
(2)根据题意可得:垂直平分,
如图,连接,则,
设,
则,解得,
∴.
23、【答案】(1)教学楼的高度为米
(2)无人机刚好离开视线的时间为12秒
【解析】解:(1)过点B作于点G,
由题意得:,米,,
∵,,,
∴四边形为矩形,
∴米,
∵,,
∴,
∴,
∴米,
∵长为米,
∴(米),
答:教学楼的高度为米.
(2)连接并延长,交于点H,
∵米,米,
∴米,
∵米, ,
∴,
∴,米,
∴(米),
∵无人机以米/秒的速度飞行,
∴离开视线的时间为:(秒),
答:无人机刚好离开视线的时间为12秒.
24、【答案】(1)见解析 (2)5
【解析】(1)证明:∵D是的中点,
∴,
∵,是的直径,
∴,
∴,
∴,
∴.
(2)解:∵,是的直径,
∴,
∵,
设,
∴,
∵,
∴,
∴,
∴,
中,,
∴,
解得或(舍去),
∴,
∴的半径为5.
25、【答案】(1)①见解析;②不变化,,理由见解析;③,理由见解析;(2),理由见解析
【解析】
【详解】(1)①证明:∵四边形是正方形,
∴,
∵,
∴,
∴;
②的大小不发生变化,;
证明:如图所示,作,垂足分别为点M、N,
∵四边形是正方形,
∴,,
∴四边形是矩形,,
∴,
∵,
∴,
∴,
∵,
∴,即;
③;
证明:如图所示,作交于点E,作于点F,
∵四边形是正方形,
∴,,
∴,四边形是矩形,
∴,
∴,
∵,,
∴,
作于点M,
则,
∴,
∵,
∴,
∴;
(2);
证明:∵四边形是菱形,,
∴,
∴是等边三角形,垂直平分,
∴,
∵,
∴,
作交于点E,交于点G,如图所示,
则四边形是平行四边形,,,
∴,都是等边三角形,
∴,
作于点M,则,
∴,
∴.
26、【答案】(1)
(2)存在,理由见详解
(3)存在点P,直线的解析式为或.
【解析】解:(1)抛物线与x轴交于点,
得,
解得:;
(2)存在,理由如下:
设与轴交于点,由(1)中结论,得抛物线的解析式为,
当时,,即,
,,即是等腰直角三角形,
,
,
,
设,过点作轴交于点,作于点,
,即是等腰直角三角形,
设直线的解析式为,代入,
得,解得,
所以直线的解析式为,
将直线向下平移个单位长度,得直线的解析式为,
,
,
当时,有最大值,
此时也有最大值,;
(3)存在点P,理由如下:
当点在直线下方时,如图所示,
在轴上取点,作直线交抛物线于(异于点)点,
由(2)中结论,得,
,
,
,
,
设直线的解析式为,代入点,
得,解得,
所以直线的解析式为;
当点在直线上方时,如图所示,在轴上取点,连接,过点作交抛物线于点,
∴,
∴,
,
,
,
设直线的解析式为,代入点,
得,解得,
设直线的解析式为,
,且过点,
设直线的解析式为,
∴,
解得,
所以直线的解析式为.
综上可知:直线的解析式为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖南省衡阳市数学中考真题名师详解版
一、选择题(本大题共12个小题,每小题3分,满分36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 中国是最早采用正负数表示相反意义量、并进行负数运算的国家.若收入500元记作元,则支出237元记作( )
A. 元 B. 元 C. 0元 D. 元
2. 下列长度的各组线段能组成一个三角形的是( )
A. B.
C. D.
3. 下面四种化学仪器的示意图是轴对称图形的是( )
A. B. C. D.
4. 作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从左面看到的图形的是( )
A. B. C. D.
5. 计算的结果正确的是( )
A. B. C. D.
6. 据共青团中央2023年5月3日发布的中国共青团团内统计公报,截至2022年12月底,全国共有共青团员7358万.数据7358万用科学记数法表示为( )
A. B. C. D.
7. 对于二次根式的乘法运算,一般地,有.该运算法则成立的条件是( )
A. B. C. D.
8. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )
A. AB=CD B. AB∥CD C. ∠A=∠C D. BC=AD
9. 《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设有x只鸡,y只兔.依题意,可列方程组为( )
A. B.
C. D.
10. 某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如下表.甲、乙两名选手成绩的方差分别记为和,则与的大小关系是( )
测试次数 1 2 3 4 5
甲 5 10 9 3 8
乙 8 6 8 6 7
A. B. C. D. 无法确定
11. 我们可以用以下推理来证明“在一个三角形中,至少有一个内角小于或等于”.假设三角形没有一个内角小于或等于,即三个内角都大于.则三角形的三个内角的和大于,这与“三角形的内角和等于”这个定理矛盾.所以在一个三角形中,至少有一个内角小于或等于.上述推理使用的证明方法是( )
A. 反证法 B. 比较法 C. 综合法 D. 分析法
12. 已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A. B. C. D.
二、填空题(本大题共6个小题,每小题3分,满分18分.)
13. 在平面直角坐标系中,点所在象限是第________象限.
14. 一个布袋中放着3个红球和9个黑球,这两种球除了颜色以外没有任何其他区别.布袋中的球已经搅匀.从布袋中任取1个球,取出红球的概率是________.
15. 已知,则代数式的值为________.
16. 已知关于x的方程的一个根是,则它的另一个根是________.
17. 如图,在中,.以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为________.
18. 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是________ 个.
三、解答题(本大题共8个小题,19~20题每题6分,21~24题每题8分,25题10分,26题12分,满分66分.解答应写出文字说明、证明过程或演算步骤.)
19. 计算:
20. 解不等式组:
21. 2023年3月27日是第28个全国中小学生安全教育日,为提高学生安全防范意识和自我防护能力,某学校举行了校园安全知识竞赛活动.现从八、九年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,80分及以上为优秀,共分成四组,A:;B:;C:;D:),并给出下面部分信息:
八年级抽取的学生竞赛成绩在C组中的数据为:84,84,88.
九年级抽取的学生竞赛成绩为:68,77,75,100,80,100,82,86,95,91,100,86,84,94,87.
八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 优秀率
八 87 a 98
九 87 86 b c
根据以上信息,解答下列问题:
(1)填空:________,________,________.
(2)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数.
22. 如图,正比例函数的图象与反比例函数的图象相交于点A.
(1)求点A的坐标.
(2)分别以点O、A为圆心,大于一半的长为半径作圆弧,两弧相交于点B和点C,作直线,交x轴于点D.求线段的长.
23. 随着科技的发展,无人机已广泛应用于生产生活,如代替人们在高空测量距离和高度.圆圆要测量教学楼的高度,借助无人机设计了如下测量方案:如图,圆圆在离教学楼底部米的C处,遥控无人机旋停在点C的正上方的点D处,测得教学楼的顶部B处的俯角为,长为米.已知目高为米.
(1)求教学楼高度.
(2)若无人机保持现有高度沿平行于方向,以米/秒的速度继续向前匀速飞行,求经过多少秒时,无人机刚好离开圆圆的视线.
24. 如图,是的直径,是一条弦,D是的中点,于点E,交于点F,交于点H,交于点G.
(1)求证:.
(2)若,求半径.
25. (1)[问题探究]
如图1,正方形中,对角线相交于点O.在线段上任取一点P(端点除外),连接.
①求证:;
②将线段绕点P逆时针旋转,使点D落在的延长线上的点Q处.当点P在线段上的位置发生变化时,的大小是否发生变化?请说明理由;
③探究与的数量关系,并说明理由.
(2)[迁移探究]
如图2,将正方形换成菱形,且,其他条件不变.试探究与的数量关系,并说明理由.
26. 如图,已知抛物线与x轴交于点和点B,与y轴交于点C,连接,过B、C两点作直线.
(1)求a的值.
(2)将直线向下平移个单位长度,交抛物线于、两点.在直线上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线的距离最大,若存在,请求出点D的坐标;若不存在,请说明理由.
(3)抛物线上是否存在点P,使,若存在,请求出直线的解析式;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】因为收入500元记作元,
所以支出237元记作元,
因此选B.
2、【答案】D
【解析】A.,此项不符合题意;
B.,此项不符合题意;
C.,此项不符合题意;
D.,此项符合题意,
因此选D.
3、【答案】C
【解析】解:A.不是轴对称图形,本选项不合题意;
B.不是轴对称图形,本选项不符合题意;
C.是轴对称图形,本选项合题意;
D.不是轴对称图形,本选项不合题意.
因此选:C.
4、【答案】B
【解析】A. 是从上向下看得到的图形为俯视图,故A项不合题意;
B. 是从左向右看得到的图形为左视图,故B项符合题意;
C. 是从下往上看得到的图形是仰视图,故C项不合题意;
D. 是从前往后看得到的图形是主视图,故D项不合题意.
因此选B.
5、【答案】B
【解析】解:,
因此选:B.
6、【答案】A
【解析】7358万,
因此选:A.
7、【答案】D
【解析】解:根据二次根式有意义的条件,得,
,
因此选:D.
8、【答案】A
【解析】解:A、当BC∥AD,AB=CD时,不能判定四边形ABCD是平行四边形,所以此选项符合题意;
B、当AB∥CD,BC∥AD时,依据两组对边分别平行的四边形是平行四边形,能判定四边形ABCD是平行四边形,所以此选项不合题意;
C、当BC∥AD,∠A=∠C时,可推出AB∥DC,依据两组对边分别平行的四边形是平行四边形,能判定四边形ABCD是平行四边形,所以此选项不合题意;
D、当BC∥AD,BC=AD时,依据一组对边平行且相等的四边形是平行四边形,能判定四边形ABCD是平行四边形,所以此选项不合题意;
因此选:A.
9、【答案】C
【解析】解:设有x只鸡,y只兔,
根据题意得:,
因此选:C.
10、【答案】A
【解析】解:甲的平均数为,
甲的方差为,
乙的平均数为,
乙的方差为,
因为,
所以.
因此选:A.
11、【答案】A
【解析】解:假设三角形没有一个内角小于或等于,即三个内角都大于.
则三角形的三个内角的和大于,
这与“三角形的内角和等于”这个定理矛盾.
所以在一个三角形中,至少有一个内角小于或等于.
以上步骤符合反证法的步骤.
所以推理使用的证明方法是反证法.
因此选:A.
12、【答案】B
【解析】解:如图,设直线与抛物线交于A、B两点,直线与抛物线交于C、D两点,
∵,关于x的方程的解为,关于x的方程的解为,
∴分别是A、B、C、D的横坐标,
∴,
因此选B.
填空题
13、【答案】三
【解析】解:的横坐标为负数,纵坐标为负数,
在第三象限,
因此答案为:三.
14、【答案】##0.25
【解析】因为一个布袋中放着3个红球和9个黑球,
所以取出红球的概率是,
因此答案为:.
15、【答案】
【解析】解:原式=
因此答案为:
16、【答案】5
【解析】解:由题意可得:,
∴,
∵该方程一个根为,令,
∴,解得:.
因此答案:5.
17、【答案】
【解析】因为,
所以,
根据切线的性质,得到圆的半径等于边上的高,
因为,
所以,
因此答案:.
18、【答案】10
【解析】解:由题意得:
∵正五边形的一个外角,
∴,
∴,
∴共需要正五边形的个数(个),
因此答案为:10.
解答题
19、【答案】
【解析】解:
20、【答案】
【解析】解:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
21、【答案】(1)84,100,;
(2)200人
【解析】解:(1)∵一共抽取八年级学生15人,
∴中位数是排序后的第8个数据,
∵1+5=6,
∴第8个数据落在C组,
∴a第八名学生成绩,即;
∵抽取的九年级学生竞赛成绩中,100分出现了3次,出现次数最多,
∴,
∵抽取的九年级学生竞赛成绩中,80分及以上的有12个,
∴;
因此答案为:84,100,;
(2)由频数分布直方图可知,抽取的八年级学生竞赛成绩中,90分以上的有6个;
根据抽取的九年级学生的竞赛成绩可得,90分以上的有6个;
所以该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数为:(人),
答:该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数为200人.
22、【答案】(1)
(2)
【解析】解:(1)解方程组,得,
∵,
∴;
(2)根据题意可得:垂直平分,
如图,连接,则,
设,
则,解得,
∴.
23、【答案】(1)教学楼的高度为米
(2)无人机刚好离开视线的时间为12秒
【解析】解:(1)过点B作于点G,
由题意得:,米,,
∵,,,
∴四边形为矩形,
∴米,
∵,,
∴,
∴,
∴米,
∵长为米,
∴(米),
答:教学楼的高度为米.
(2)连接并延长,交于点H,
∵米,米,
∴米,
∵米, ,
∴,
∴,米,
∴(米),
∵无人机以米/秒的速度飞行,
∴离开视线的时间为:(秒),
答:无人机刚好离开视线的时间为12秒.
24、【答案】(1)见解析 (2)5
【解析】(1)证明:∵D是的中点,
∴,
∵,是的直径,
∴,
∴,
∴,
∴.
(2)解:∵,是的直径,
∴,
∵,
设,
∴,
∵,
∴,
∴,
∴,
中,,
∴,
解得或(舍去),
∴,
∴的半径为5.
25、【答案】(1)①见解析;②不变化,,理由见解析;③,理由见解析;(2),理由见解析
【解析】
【详解】(1)①证明:∵四边形是正方形,
∴,
∵,
∴,
∴;
②的大小不发生变化,;
证明:如图所示,作,垂足分别为点M、N,
∵四边形是正方形,
∴,,
∴四边形是矩形,,
∴,
∵,
∴,
∴,
∵,
∴,即;
③;
证明:如图所示,作交于点E,作于点F,
∵四边形是正方形,
∴,,
∴,四边形是矩形,
∴,
∴,
∵,,
∴,
作于点M,
则,
∴,
∵,
∴,
∴;
(2);
证明:∵四边形是菱形,,
∴,
∴是等边三角形,垂直平分,
∴,
∵,
∴,
作交于点E,交于点G,如图所示,
则四边形是平行四边形,,,
∴,都是等边三角形,
∴,
作于点M,则,
∴,
∴.
26、【答案】(1)
(2)存在,理由见详解
(3)存在点P,直线的解析式为或.
【解析】解:(1)抛物线与x轴交于点,
得,
解得:;
(2)存在,理由如下:
设与轴交于点,由(1)中结论,得抛物线的解析式为,
当时,,即,
,,即是等腰直角三角形,
,
,
,
设,过点作轴交于点,作于点,
,即是等腰直角三角形,
设直线的解析式为,代入,
得,解得,
所以直线的解析式为,
将直线向下平移个单位长度,得直线的解析式为,
,
,
当时,有最大值,
此时也有最大值,;
(3)存在点P,理由如下:
当点在直线下方时,如图所示,
在轴上取点,作直线交抛物线于(异于点)点,
由(2)中结论,得,
,
,
,
,
设直线的解析式为,代入点,
得,解得,
所以直线的解析式为;
当点在直线上方时,如图所示,在轴上取点,连接,过点作交抛物线于点,
∴,
∴,
,
,
,
设直线的解析式为,代入点,
得,解得,
设直线的解析式为,
,且过点,
设直线的解析式为,
∴,
解得,
所以直线的解析式为.
综上可知:直线的解析式为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
