2023年湖南省娄底市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖南省娄底市数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年湖南省娄底市数学中考真题名师详解版
温馨提示:
1.本学科试卷分试题卷和答题卡两部分,数学卷面满分120分,考试时量120分钟.
2.请你将姓名、准考证号等相关信息按要求填涂在答题卡上.
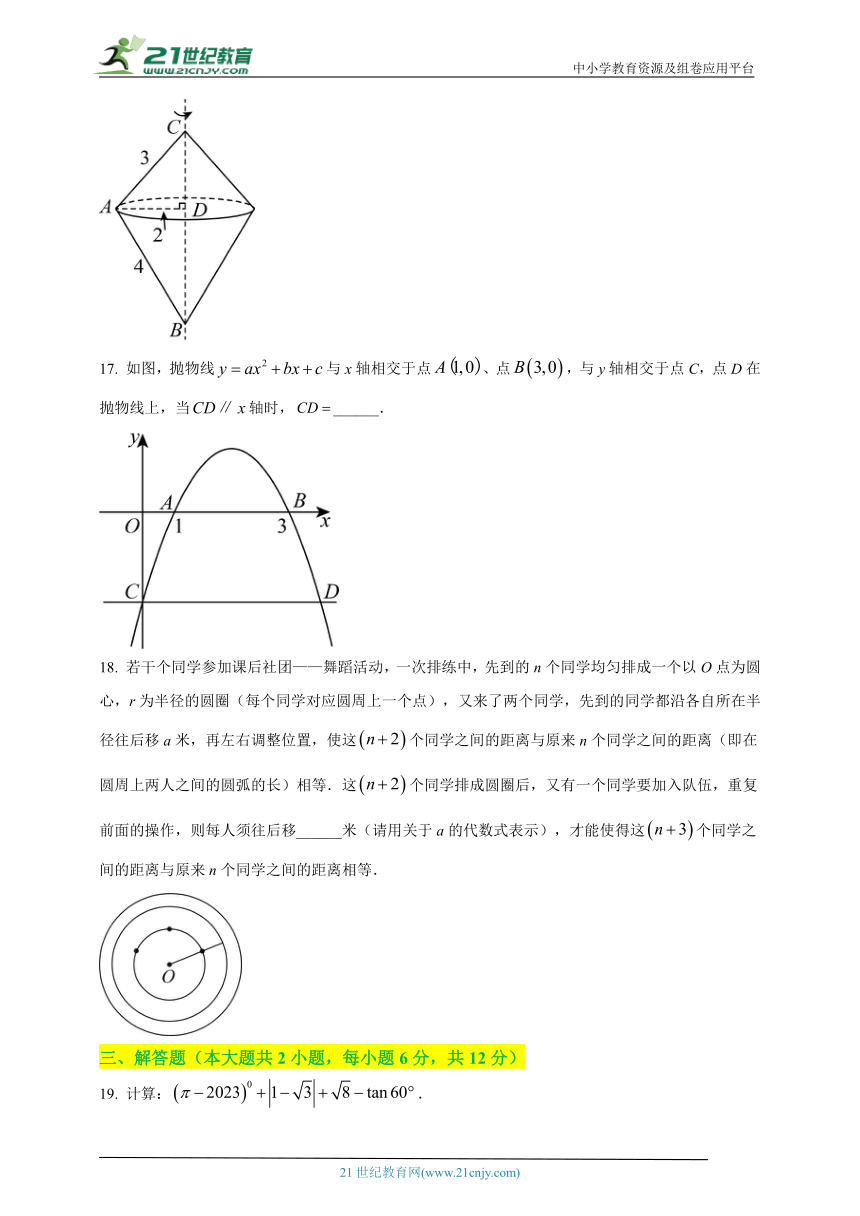
3.请你在答题卡规定区域内作答,答在本试题卷上无效.
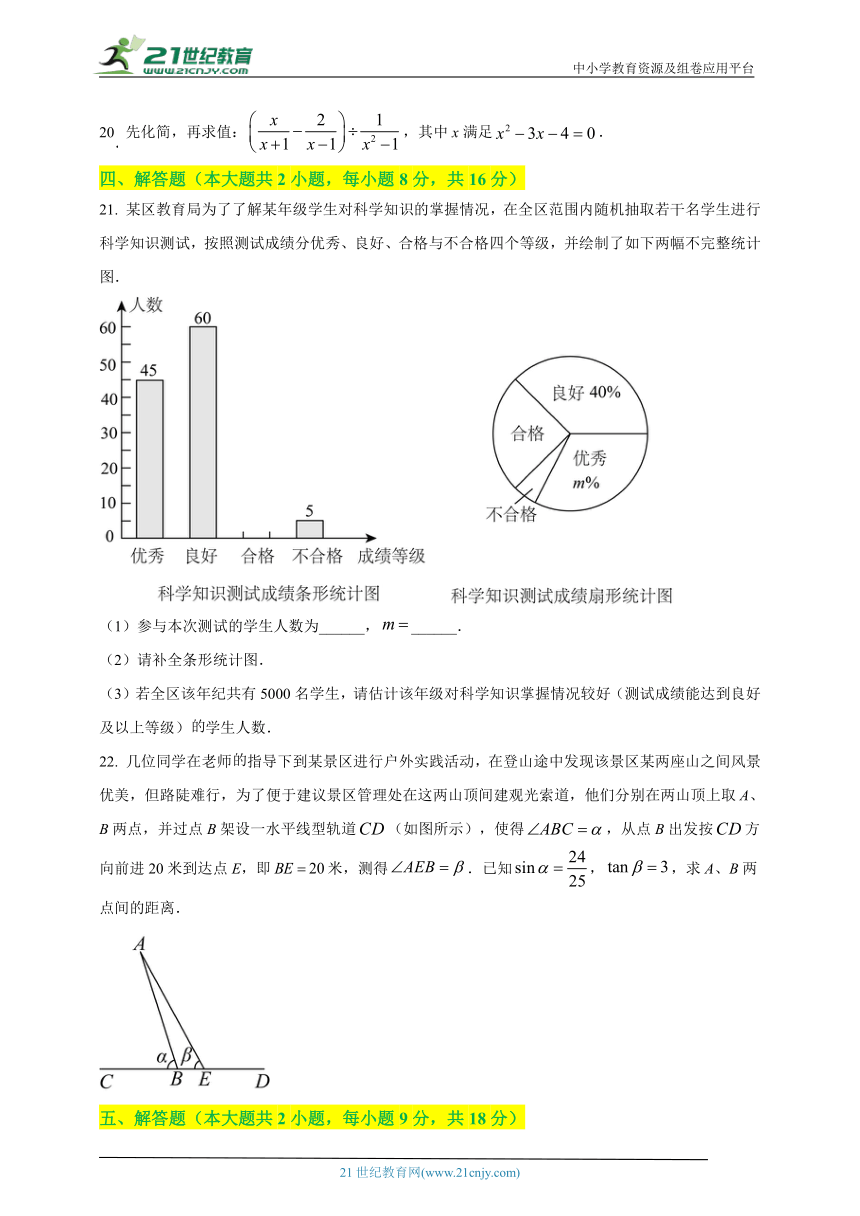
一、选择题(本大题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一个选项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1. 的倒数是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 新时代我国教育事业取得了历史性成就,目前我国已建成世界上规模最大的教育体系,教育现代化发展总体水平跨入世界中上国家行列,其中高等教育在学总规模达到4430万人,处于高等教育普及化阶段.4430万用科学记数法表示为( )
A. B. C. D.
4. 一个小组7名同学的身高(单位:)分别为:175,160,158,155,168,151,170.这组数据的中位数是( )
A. 151 B. 155 C. 158 D. 160
5. 不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
6. 将直线向右平移2个单位所得直线的表达式为( )
A. B. C. D.
7. 从,3.1415926,,,,,中随机抽取一个数,此数是无理数的概率是( )
A. B. C. D.
8. 一个长方体物体的一顶点所在A、B、C三个面的面积比是,如果分别按A、B、C面朝上将此物体放在水平地面上,地面所受的压力产生的压强分别为、、(压强的计算公式为),则( )
A. B. C. D.
9. 如图,正六边形的外接圆的半径为2,过圆心O的两条直线、的夹角为,则图中的阴影部分的面积为( )
A. B. C. D.
10. 已知二次函数的图象如图所示,给出下列结论:①;②;③(m为任意实数);④若点和点在该图象上,则.其中正确的结论是( )
A ①② B. ①④ C. ②③ D. ②④
11. 从n个不同元素中取出个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示,(,n、m为正整数);例如:,,则( )
A. B. C. D.
12. 我国南宋著名数学家秦九韶在他的著作《数学九章》一书中,给出了这样的一个结论:三边分别为a、b、c的的面积为.的边a、b、c所对的角分别是∠A、∠B、∠C,则.下列结论中正确的是( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,满分18分)
13. 函数y=的自变量x的取值范围为____________.
14. 若m是方程的根,则______.
15. 如图,点E在矩形的边上,将沿折叠,点D恰好落在边上的点F处,若.,则______.
16. 如图,在中,,,边上的高,将绕着所在的直线旋转一周得到的几何体的表面积为______.
17. 如图,抛物线与x轴相交于点、点,与y轴相交于点C,点D在抛物线上,当轴时,______.
18. 若干个同学参加课后社团——舞蹈活动,一次排练中,先到的n个同学均匀排成一个以O点为圆心,r为半径的圆圈(每个同学对应圆周上一个点),又来了两个同学,先到的同学都沿各自所在半径往后移a米,再左右调整位置,使这个同学之间的距离与原来n个同学之间的距离(即在圆周上两人之间的圆弧的长)相等.这个同学排成圆圈后,又有一个同学要加入队伍,重复前面的操作,则每人须往后移______米(请用关于a的代数式表示),才能使得这个同学之间的距离与原来n个同学之间的距离相等.
三、解答题(本大题共2小题,每小题6分,共12分)
19. 计算:.
20 先化简,再求值:,其中x满足.
四、解答题(本大题共2小题,每小题8分,共16分)
21. 某区教育局为了了解某年级学生对科学知识的掌握情况,在全区范围内随机抽取若干名学生进行科学知识测试,按照测试成绩分优秀、良好、合格与不合格四个等级,并绘制了如下两幅不完整统计图.
(1)参与本次测试的学生人数为______,______.
(2)请补全条形统计图.
(3)若全区该年纪共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)学生人数.
22. 几位同学在老师指导下到某景区进行户外实践活动,在登山途中发现该景区某两座山之间风景优美,但路陡难行,为了便于建议景区管理处在这两山顶间建观光索道,他们分别在两山顶上取A、B两点,并过点B架设一水平线型轨道(如图所示),使得,从点B出发按方向前进20米到达点E,即米,测得.已知,,求A、B两点间的距离.
五、解答题(本大题共2小题,每小题9分,共18分)
23. 为落实“五育并举”,绿化美化环境,学校在劳动周组织学生到校园周边种植甲、乙两种树苗.已知购买甲种树苗3棵,乙种树苗2棵共需12元,;购买甲种树苗1棵,乙种树苗3棵共需11元.
(1)求每棵甲、乙树苗的价格.
(2)本次活动共种植了200棵甲、乙树苗,假设所种的树苗若干年后全部长成了参天大树,并且平均每棵树的价值(含生态价值,经济价值)均为原来树苗价的100倍,要想获得不低于5万元的价值,请问乙种树苗种植数量不得少于多少棵?
24. 如图1,点为等边的重心,点为边的中点,连接并延长至点,使得,连接,,,
(1)求证:四边形为菱形.
(2)如图2,以点圆心,为半径作
①判断直线与的位置关系,并予以证明.
②点为劣弧上一动点(与点、点不重合),连接并延长交于点,连接并延长交于点,求证:为定值.
六、综合题(本大题共2小题,每小题10分,共20分)
25. 鲜艳的中华人民共和国国旗始终是当代中华儿女永不褪色的信仰,国旗上的每颗星都是标准五角星.为了增强学生的国家荣誉感、民族自豪感等.数学老师组织学生对五角星进行了较深入的研究.延长正五边形的各边直到不相邻的边相交,得到一个标准五角星.如图,正五边形的边的延长线相交于点F,的平分线交于点M.
(1)求证:.
(2)若,求的长.
(3)求的值.
26. 如图,抛物线过点、点,交y轴于点C.
(1)求b,c的值.
(2)点是抛物线上的动点
①当取何值时,的面积最大?并求出面积的最大值;
②过点P作轴,交于点E,再过点P作轴,交抛物线于点F,连接,问:是否存在点P,使为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:因为,
所以倒数是,
因此选:.
2、【答案】D
【解析】解:,所以A不符合题意;
,不是同类项,不能合并,所以B不符合题意;
,所以C不符合题意;
,运算正确,所以D符合题意;
因此选D
3、【答案】B
【解析】解:4430万,
因此选:B.
4、【答案】D
【解析】解:由于此数据按照从小到大的顺序排列为151,155,158,160,168,170,175.
发现160处于第4位.所以这组数据的中位数是160,
因此选:D.
5、【答案】C
【解析】解:,
解①得:,
解②得:,
在数轴上表示两个不等式的解集如下:
所以不等式组的解集为:;
因此选:C
6、【答案】B
【解析】解:将直线向右平移2个单位,
所得直线的解析式为,
即,
因此选:B.
7、【答案】A
【解析】解:∵,,
∴,3.1415926,,,,,中无理数有:,,
∴从,3.1415926,,,,,中随机抽取一个数,这个数是无理数的概率是;
因此选:A
8、【答案】A
【解析】解:∵长方体物体的一顶点所在A、B、C三个面的面积比是,
∴长方体物体的A、B、C三面所对的与水平地面接触的面积比也为,
∵,,且一定,
∴随的增大而减小,
∴.
因此选:A.
9、【答案】C
【解析】解:如图所示,连接,标注直线与圆的交点,
由正六边形的性质可得:,,三点共线,为等边三角形,
∴,,
∴,
∴扇形与扇形重合,
∴,
∵为等边三角形,,过作于,
∴,,,
∴;
因此选:C
10、【答案】D
【解析】解:∵抛物线的开口向下,与y轴交于正半轴,对称轴在y轴的左边,
∴,,,
∴,
∴,所以①不符合题意;
∵对称轴为直线,
∴当与时的函数值相等,
∴,所以②符合题意;
∵当时函数值最大,
∴,
∴;所以③不符合题意;
∵点和点在该图象上,
而,且离抛物线的对称轴越远的点的函数值越小,
∴.所以④符合题意;
因此选:D.
11、【答案】C
【解析】解:∵,
∴,
A项,,
B项,,
C项,,
D项,,
因此选:C.
12、【答案】A
【解析】解:∵,,
∴
即,
,
,
因此选:A.
填空题
13、【答案】x≥-1
【解析】根据题意得,x+1≥0,
解得x≥﹣1.
因此答案为x≥﹣1.
14、【答案】6
【解析】解:∵m是方程的根,
∴,即,
∴
;
因此答案为:6.
15、【答案】5
【解析】解:∵四边形是矩形,
∴,,,
根据折叠可知,可知,,
则在中,,则,
∴,则,
设,则,
在中,,即:,
解得:,
即,
因此答案为:5.
16、【答案】
【解析】解:根据题意得:旋转后的几何体是两个共底面的圆锥,
∵边上的高,
∴底面圆的周长为:,
∵,,
∴几何体的表面积为.
因此答案为:.
17、【答案】4
【解析】解:∵抛物线与x轴相交于点、点,
∴抛物线的对称轴为,
∵当时,,即,
∵轴,
∴,关于直线对称,
∴,
∴;
因此答案为:4
18、【答案】
【解析】解:由第一次操作得:,
∴,
设第二次操作时每位同学向后移动了x米,则
,
∴,
因此答案为:
解答题
19、【答案】
【解析】解:
.
20、【答案】;2
【解析】解:
;
∵,
∴,其中,
∴原式.
解答题
21、【答案】(1)150人,
(2)补全图形见解析 (3)3500人.
【解析】解:(1)(人),
∴参与本次测试的学生人数为150人,
,
∴;
因此答案为:人;30;
(2)∵(人),
补全条形图如下:
.
(3)(人);
所以全区该年纪共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)的学生人数有3500人.
22、【答案】A、B两点间的距离为500米.
【解析】解:如图所示,过点作于点,
∵,即,
设,则,
∴,而,
∴,
∵,
∴,即,
∴,
解得:,
∴(米),
答:A、B两点间的距离为500米.
解答题
23、【答案】(1)每棵甲种树苗的价格为2元,每棵乙种树苗的价格3元;
(2)乙种树苗种植数量不得少于100棵.
【解析】解:(1)设每棵甲种树苗的价格为x元,每棵乙种树苗的价格y元, 根据题意得:
, 解得:,
答:每棵甲种树苗的价格为2元,每棵乙种树苗的价格3元;
(2)设乙种树苗种植数量为m棵,则甲种树苗数量为棵,
∴,
解得:,
∴的最小整数解为100.
答:乙种树苗种植数量不得少于100棵.
24、【答案】(1)见解析;
(2)①直线是的切线;②见解析.
【解析】证明:如图,延长交于点,连接,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,
∴ ,,
∵,
∴四边形是平行四边形,
∵ ,
∴四边形为菱形;
(2)①解:直线是的切线,理由如下:延长交于点,连接,如图所示,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,,
∴为的角平分线,
∴,
∵四边形是菱形,
∴,
∴,
∴,
∴直线是的切线;
②证明:在优弧上取一点,连接、,如图所示,
由①得,
∵,
∴,
∴,
∴,
∵四边形内接于,
∴,
∴,
∵,
∴,
∴,
∵,,
∴
∴
∵
∴,即为定值.
综合题
25、【答案】(1)见解析 (2) (3)
【解析】(1)证明:∵是正五边形,
∴,
∴,
又∵的平分线交于点M,
∴,
∴,
又∵,
∴,
∴,
即;
(2)解:∵,
∴,
∴,,
∵,
∴,
解得:或(舍去),
∴;
(3)解:设,,连接,,
则根据(2)中计算可得,
∵是正五边形,
∴,
∴
∴,
∴,,
∴,
∴,
∴,
∴.
26、【答案】(1),
(2)①当时,的面积由最大值,最大值为;
②当点的坐标为或时,为等腰直角三角形
【解析】解:(1)将、代入抛物线中,
得:,解得:,
即:,;
(2)①由(1)可知:,
当时,,即,
设的解析式为:,
将,代入中,
可得,解得:,
所以的解析式为:,
过点P作轴,交于点E,交轴于点,
∵,则,
∴点E的横坐标也为,则纵坐标为,
∴,
的面积
,
∵,
∴当时,的面积有最大值,最大值为;
②存在,当点的坐标为或时,为等腰直角三角形.
理由如下:由①可知,
由题意可知抛物线的对称轴为直线,
∵轴,
∴,,则,
当点在对称轴左侧时,即时,
,当时,为等腰直角三角形,
即:,整理得:,
解得:(,不符合题意,舍去)
此时,即点;
当点在对称轴右侧时,即时,
,当时,为等腰直角三角形,
即:,整理得:,
解得:(,不符合题意,舍去)
此时:,即点;
综上,当点的坐标为或时,为等腰直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖南省娄底市数学中考真题名师详解版
温馨提示:
1.本学科试卷分试题卷和答题卡两部分,数学卷面满分120分,考试时量120分钟.
2.请你将姓名、准考证号等相关信息按要求填涂在答题卡上.
3.请你在答题卡规定区域内作答,答在本试题卷上无效.
一、选择题(本大题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一个选项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1. 的倒数是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 新时代我国教育事业取得了历史性成就,目前我国已建成世界上规模最大的教育体系,教育现代化发展总体水平跨入世界中上国家行列,其中高等教育在学总规模达到4430万人,处于高等教育普及化阶段.4430万用科学记数法表示为( )
A. B. C. D.
4. 一个小组7名同学的身高(单位:)分别为:175,160,158,155,168,151,170.这组数据的中位数是( )
A. 151 B. 155 C. 158 D. 160
5. 不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
6. 将直线向右平移2个单位所得直线的表达式为( )
A. B. C. D.
7. 从,3.1415926,,,,,中随机抽取一个数,此数是无理数的概率是( )
A. B. C. D.
8. 一个长方体物体的一顶点所在A、B、C三个面的面积比是,如果分别按A、B、C面朝上将此物体放在水平地面上,地面所受的压力产生的压强分别为、、(压强的计算公式为),则( )
A. B. C. D.
9. 如图,正六边形的外接圆的半径为2,过圆心O的两条直线、的夹角为,则图中的阴影部分的面积为( )
A. B. C. D.
10. 已知二次函数的图象如图所示,给出下列结论:①;②;③(m为任意实数);④若点和点在该图象上,则.其中正确的结论是( )
A ①② B. ①④ C. ②③ D. ②④
11. 从n个不同元素中取出个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示,(,n、m为正整数);例如:,,则( )
A. B. C. D.
12. 我国南宋著名数学家秦九韶在他的著作《数学九章》一书中,给出了这样的一个结论:三边分别为a、b、c的的面积为.的边a、b、c所对的角分别是∠A、∠B、∠C,则.下列结论中正确的是( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,满分18分)
13. 函数y=的自变量x的取值范围为____________.
14. 若m是方程的根,则______.
15. 如图,点E在矩形的边上,将沿折叠,点D恰好落在边上的点F处,若.,则______.
16. 如图,在中,,,边上的高,将绕着所在的直线旋转一周得到的几何体的表面积为______.
17. 如图,抛物线与x轴相交于点、点,与y轴相交于点C,点D在抛物线上,当轴时,______.
18. 若干个同学参加课后社团——舞蹈活动,一次排练中,先到的n个同学均匀排成一个以O点为圆心,r为半径的圆圈(每个同学对应圆周上一个点),又来了两个同学,先到的同学都沿各自所在半径往后移a米,再左右调整位置,使这个同学之间的距离与原来n个同学之间的距离(即在圆周上两人之间的圆弧的长)相等.这个同学排成圆圈后,又有一个同学要加入队伍,重复前面的操作,则每人须往后移______米(请用关于a的代数式表示),才能使得这个同学之间的距离与原来n个同学之间的距离相等.
三、解答题(本大题共2小题,每小题6分,共12分)
19. 计算:.
20 先化简,再求值:,其中x满足.
四、解答题(本大题共2小题,每小题8分,共16分)
21. 某区教育局为了了解某年级学生对科学知识的掌握情况,在全区范围内随机抽取若干名学生进行科学知识测试,按照测试成绩分优秀、良好、合格与不合格四个等级,并绘制了如下两幅不完整统计图.
(1)参与本次测试的学生人数为______,______.
(2)请补全条形统计图.
(3)若全区该年纪共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)学生人数.
22. 几位同学在老师指导下到某景区进行户外实践活动,在登山途中发现该景区某两座山之间风景优美,但路陡难行,为了便于建议景区管理处在这两山顶间建观光索道,他们分别在两山顶上取A、B两点,并过点B架设一水平线型轨道(如图所示),使得,从点B出发按方向前进20米到达点E,即米,测得.已知,,求A、B两点间的距离.
五、解答题(本大题共2小题,每小题9分,共18分)
23. 为落实“五育并举”,绿化美化环境,学校在劳动周组织学生到校园周边种植甲、乙两种树苗.已知购买甲种树苗3棵,乙种树苗2棵共需12元,;购买甲种树苗1棵,乙种树苗3棵共需11元.
(1)求每棵甲、乙树苗的价格.
(2)本次活动共种植了200棵甲、乙树苗,假设所种的树苗若干年后全部长成了参天大树,并且平均每棵树的价值(含生态价值,经济价值)均为原来树苗价的100倍,要想获得不低于5万元的价值,请问乙种树苗种植数量不得少于多少棵?
24. 如图1,点为等边的重心,点为边的中点,连接并延长至点,使得,连接,,,
(1)求证:四边形为菱形.
(2)如图2,以点圆心,为半径作
①判断直线与的位置关系,并予以证明.
②点为劣弧上一动点(与点、点不重合),连接并延长交于点,连接并延长交于点,求证:为定值.
六、综合题(本大题共2小题,每小题10分,共20分)
25. 鲜艳的中华人民共和国国旗始终是当代中华儿女永不褪色的信仰,国旗上的每颗星都是标准五角星.为了增强学生的国家荣誉感、民族自豪感等.数学老师组织学生对五角星进行了较深入的研究.延长正五边形的各边直到不相邻的边相交,得到一个标准五角星.如图,正五边形的边的延长线相交于点F,的平分线交于点M.
(1)求证:.
(2)若,求的长.
(3)求的值.
26. 如图,抛物线过点、点,交y轴于点C.
(1)求b,c的值.
(2)点是抛物线上的动点
①当取何值时,的面积最大?并求出面积的最大值;
②过点P作轴,交于点E,再过点P作轴,交抛物线于点F,连接,问:是否存在点P,使为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:因为,
所以倒数是,
因此选:.
2、【答案】D
【解析】解:,所以A不符合题意;
,不是同类项,不能合并,所以B不符合题意;
,所以C不符合题意;
,运算正确,所以D符合题意;
因此选D
3、【答案】B
【解析】解:4430万,
因此选:B.
4、【答案】D
【解析】解:由于此数据按照从小到大的顺序排列为151,155,158,160,168,170,175.
发现160处于第4位.所以这组数据的中位数是160,
因此选:D.
5、【答案】C
【解析】解:,
解①得:,
解②得:,
在数轴上表示两个不等式的解集如下:
所以不等式组的解集为:;
因此选:C
6、【答案】B
【解析】解:将直线向右平移2个单位,
所得直线的解析式为,
即,
因此选:B.
7、【答案】A
【解析】解:∵,,
∴,3.1415926,,,,,中无理数有:,,
∴从,3.1415926,,,,,中随机抽取一个数,这个数是无理数的概率是;
因此选:A
8、【答案】A
【解析】解:∵长方体物体的一顶点所在A、B、C三个面的面积比是,
∴长方体物体的A、B、C三面所对的与水平地面接触的面积比也为,
∵,,且一定,
∴随的增大而减小,
∴.
因此选:A.
9、【答案】C
【解析】解:如图所示,连接,标注直线与圆的交点,
由正六边形的性质可得:,,三点共线,为等边三角形,
∴,,
∴,
∴扇形与扇形重合,
∴,
∵为等边三角形,,过作于,
∴,,,
∴;
因此选:C
10、【答案】D
【解析】解:∵抛物线的开口向下,与y轴交于正半轴,对称轴在y轴的左边,
∴,,,
∴,
∴,所以①不符合题意;
∵对称轴为直线,
∴当与时的函数值相等,
∴,所以②符合题意;
∵当时函数值最大,
∴,
∴;所以③不符合题意;
∵点和点在该图象上,
而,且离抛物线的对称轴越远的点的函数值越小,
∴.所以④符合题意;
因此选:D.
11、【答案】C
【解析】解:∵,
∴,
A项,,
B项,,
C项,,
D项,,
因此选:C.
12、【答案】A
【解析】解:∵,,
∴
即,
,
,
因此选:A.
填空题
13、【答案】x≥-1
【解析】根据题意得,x+1≥0,
解得x≥﹣1.
因此答案为x≥﹣1.
14、【答案】6
【解析】解:∵m是方程的根,
∴,即,
∴
;
因此答案为:6.
15、【答案】5
【解析】解:∵四边形是矩形,
∴,,,
根据折叠可知,可知,,
则在中,,则,
∴,则,
设,则,
在中,,即:,
解得:,
即,
因此答案为:5.
16、【答案】
【解析】解:根据题意得:旋转后的几何体是两个共底面的圆锥,
∵边上的高,
∴底面圆的周长为:,
∵,,
∴几何体的表面积为.
因此答案为:.
17、【答案】4
【解析】解:∵抛物线与x轴相交于点、点,
∴抛物线的对称轴为,
∵当时,,即,
∵轴,
∴,关于直线对称,
∴,
∴;
因此答案为:4
18、【答案】
【解析】解:由第一次操作得:,
∴,
设第二次操作时每位同学向后移动了x米,则
,
∴,
因此答案为:
解答题
19、【答案】
【解析】解:
.
20、【答案】;2
【解析】解:
;
∵,
∴,其中,
∴原式.
解答题
21、【答案】(1)150人,
(2)补全图形见解析 (3)3500人.
【解析】解:(1)(人),
∴参与本次测试的学生人数为150人,
,
∴;
因此答案为:人;30;
(2)∵(人),
补全条形图如下:
.
(3)(人);
所以全区该年纪共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)的学生人数有3500人.
22、【答案】A、B两点间的距离为500米.
【解析】解:如图所示,过点作于点,
∵,即,
设,则,
∴,而,
∴,
∵,
∴,即,
∴,
解得:,
∴(米),
答:A、B两点间的距离为500米.
解答题
23、【答案】(1)每棵甲种树苗的价格为2元,每棵乙种树苗的价格3元;
(2)乙种树苗种植数量不得少于100棵.
【解析】解:(1)设每棵甲种树苗的价格为x元,每棵乙种树苗的价格y元, 根据题意得:
, 解得:,
答:每棵甲种树苗的价格为2元,每棵乙种树苗的价格3元;
(2)设乙种树苗种植数量为m棵,则甲种树苗数量为棵,
∴,
解得:,
∴的最小整数解为100.
答:乙种树苗种植数量不得少于100棵.
24、【答案】(1)见解析;
(2)①直线是的切线;②见解析.
【解析】证明:如图,延长交于点,连接,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,
∴ ,,
∵,
∴四边形是平行四边形,
∵ ,
∴四边形为菱形;
(2)①解:直线是的切线,理由如下:延长交于点,连接,如图所示,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,,
∴为的角平分线,
∴,
∵四边形是菱形,
∴,
∴,
∴,
∴直线是的切线;
②证明:在优弧上取一点,连接、,如图所示,
由①得,
∵,
∴,
∴,
∴,
∵四边形内接于,
∴,
∴,
∵,
∴,
∴,
∵,,
∴
∴
∵
∴,即为定值.
综合题
25、【答案】(1)见解析 (2) (3)
【解析】(1)证明:∵是正五边形,
∴,
∴,
又∵的平分线交于点M,
∴,
∴,
又∵,
∴,
∴,
即;
(2)解:∵,
∴,
∴,,
∵,
∴,
解得:或(舍去),
∴;
(3)解:设,,连接,,
则根据(2)中计算可得,
∵是正五边形,
∴,
∴
∴,
∴,,
∴,
∴,
∴,
∴.
26、【答案】(1),
(2)①当时,的面积由最大值,最大值为;
②当点的坐标为或时,为等腰直角三角形
【解析】解:(1)将、代入抛物线中,
得:,解得:,
即:,;
(2)①由(1)可知:,
当时,,即,
设的解析式为:,
将,代入中,
可得,解得:,
所以的解析式为:,
过点P作轴,交于点E,交轴于点,
∵,则,
∴点E的横坐标也为,则纵坐标为,
∴,
的面积
,
∵,
∴当时,的面积有最大值,最大值为;
②存在,当点的坐标为或时,为等腰直角三角形.
理由如下:由①可知,
由题意可知抛物线的对称轴为直线,
∵轴,
∴,,则,
当点在对称轴左侧时,即时,
,当时,为等腰直角三角形,
即:,整理得:,
解得:(,不符合题意,舍去)
此时,即点;
当点在对称轴右侧时,即时,
,当时,为等腰直角三角形,
即:,整理得:,
解得:(,不符合题意,舍去)
此时:,即点;
综上,当点的坐标为或时,为等腰直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
