2023年湖南省邵阳市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖南省邵阳市数学中考真题名师详解版 试卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年湖南省邵阳市数学中考真题名师详解版
温馨提示:
(1)本学科试卷分试题卷和答题卡两部分,考试时量为120分钟,满分120分.
(2)请你将姓名、准考证号等相关信息按要求填涂在答题卡上.
(3)请在答题卡上作答,做在本试题卷上的答案无效.
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个项是符合题目要求的)
1. 的倒数是( )
A. B. C. D.
2. 下列四个图形中,是中心对称图形的是( )
A. B. C. D.
3. 党的二十大报告提出,要坚持以文塑旅、以旅彰文,推进文化和旅游深度融合发展.湖南是文化旅游资源大省,深挖红色文化、非遗文化和乡村文化,推进文旅产业赋能乡村振兴.湖南红色旅游区(点)2022年接待游客约165000000人次,则165000000用科学记数法可表示为( )
A. B. C. D.
4. 下列计算正确的是( )
A. B. C. D.
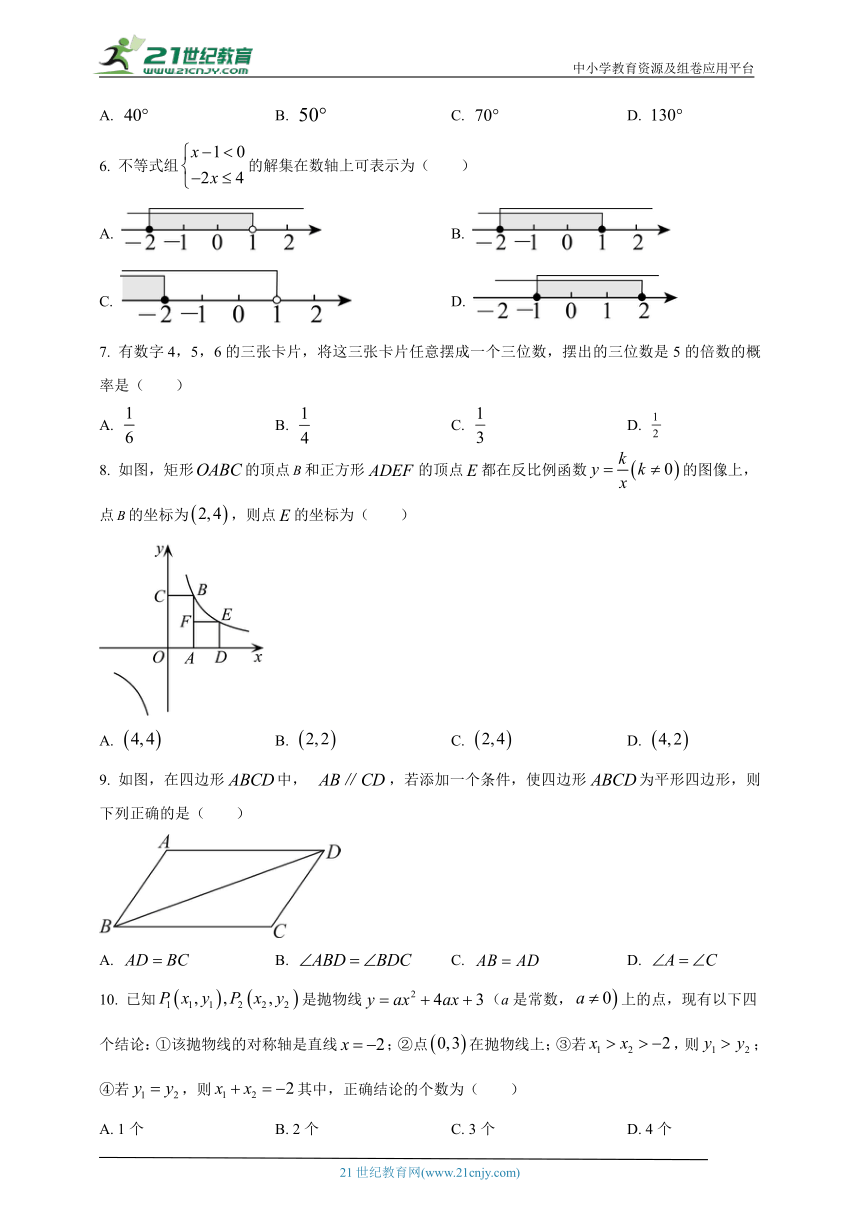
5. 如图,直线被直线所截,已知,则的大小为( )
A. B. C. D.
6. 不等式组的解集在数轴上可表示为( )
A. B.
C. D.
7. 有数字4,5,6的三张卡片,将这三张卡片任意摆成一个三位数,摆出的三位数是5的倍数的概率是( )
A. B. C. D.
8. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为,则点的坐标为( )
A. B. C. D.
9. 如图,在四边形中, ,若添加一个条件,使四边形为平形四边形,则下列正确的是( )
A. B. C. D.
10. 已知是抛物线(a是常数,上的点,现有以下四个结论:①该抛物线的对称轴是直线;②点在抛物线上;③若,则;④若,则其中,正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题有8个小题,每小题3分,共24分)
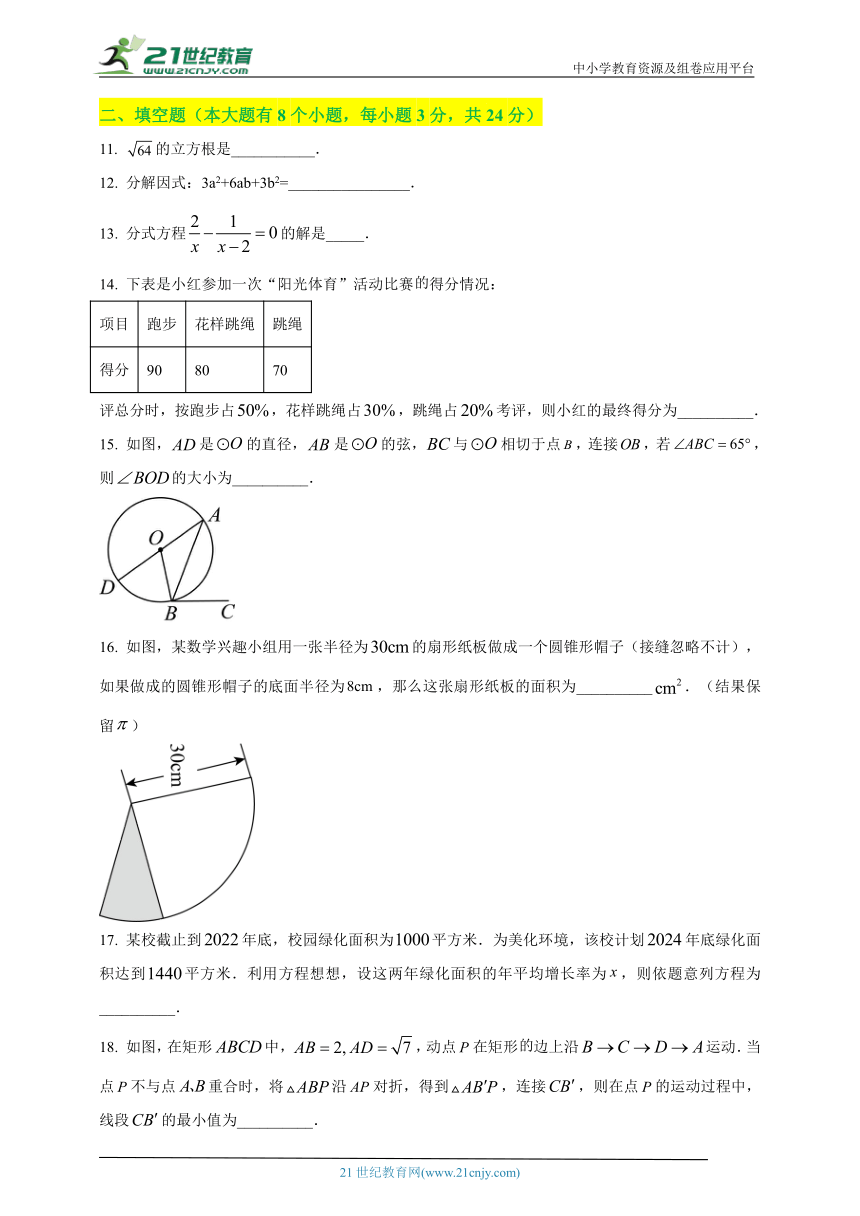
11. 的立方根是___________.
12. 分解因式:3a2+6ab+3b2=________________.
13. 分式方程的解是_____.
14. 下表是小红参加一次“阳光体育”活动比赛得分情况:
项目 跑步 花样跳绳 跳绳
得分 90 80 70
评总分时,按跑步占,花样跳绳占,跳绳占考评,则小红的最终得分为__________.
15. 如图,是的直径,是的弦,与相切于点,连接,若,则的大小为__________.
16. 如图,某数学兴趣小组用一张半径为的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为,那么这张扇形纸板的面积为__________.(结果保留)
17. 某校截止到年底,校园绿化面积为平方米.为美化环境,该校计划年底绿化面积达到平方米.利用方程想想,设这两年绿化面积的年平均增长率为,则依题意列方程为__________.
18. 如图,在矩形中,,动点在矩形边上沿运动.当点不与点重合时,将沿对折,得到,连接,则在点的运动过程中,线段的最小值为__________.
三、解答题(本大题有8个小题,第19-25题每题8分,第26题10分,共56分,解答应写出必要的文字说明、演算步骤或证明过程)
19. 计算:.
20. 先化简,再求值:,其中.
21. 如图,,点是线段上的一点,且.已知.
(1)证明:.
(2)求线段的长.
22. 低碳生活已是如今社会的一种潮流形式,人们的环保观念也在逐渐加深.低碳环保,绿色出行成为大家的生活理念,不少人选择自行车出行.某公司销售甲、乙两种型号的自行车,其中甲型自行车进货价格为每台元,乙型自行车进货价格为每台元.该公司销售台甲型自行车和台乙型自行车,可获利元,销售台甲型自行车和台乙型自行车,可获利元.
(1)该公司销售一台甲型、一台乙型自行车的利润各是多少元?
(2)为满足大众需求,该公司准备加购甲、乙两种型号的自行车共台,且资金不超过元,最少需要购买甲型自行车多少台?
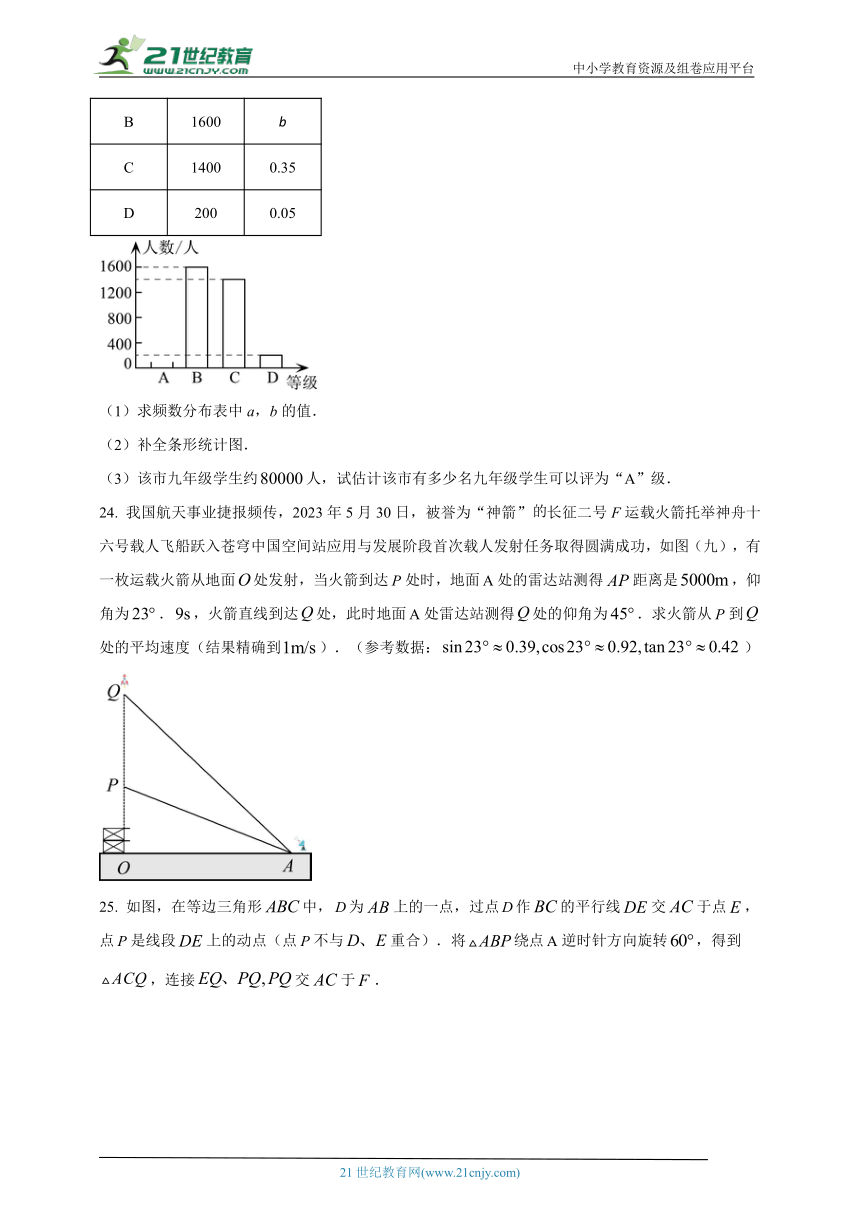
23. 某市对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中随机抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出了如下频数分布图和如图(八)所示的条形统计图(不完整).请根据图表中的信息回答下列问题.
等级 频数 频率
A a 02
B 1600 b
C 1400 0.35
D 200 0.05
(1)求频数分布表中a,b的值.
(2)补全条形统计图.
(3)该市九年级学生约人,试估计该市有多少名九年级学生可以评为“A”级.
24. 我国航天事业捷报频传,2023年5月30日,被誉为“神箭”长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹中国空间站应用与发展阶段首次载人发射任务取得圆满成功,如图(九),有一枚运载火箭从地面处发射,当火箭到达处时,地面处的雷达站测得距离是,仰角为.,火箭直线到达处,此时地面处雷达站测得处的仰角为.求火箭从到处的平均速度(结果精确到).(参考数据:)
25. 如图,在等边三角形中,为上的一点,过点作的平行线交于点,点是线段上的动点(点不与重合).将绕点逆时针方向旋转,得到,连接交于.
(1)证明:在点的运动过程中,总有.
(2)当为何值时,是直角三角形?
26. 如图,在平面直角坐标系中,抛物线经过点和点,且与直线交于两点(点在点的右侧),点为直线上的一动点,设点的横坐标为.
(1)求抛物线的解析式.
(2)过点作轴垂线,与拋物线交于点.若,求面积的最大值.
(3)抛物线与轴交于点,点为平面直角坐标系上一点,若以为顶点的四边形是菱形,请求出所有满足条件的点的坐标.
参考答案及解析
一、选择题
1、【答案】C
【解析】解:的倒数为.
因此选:C.
2、【答案】A
【解析】解:A选项,是中心对称图形,所以符合题意;
B选项,不是中心对称图形,所以不符合题意;
C选项,不是中心对称图形,所以不符合题意;
D选项,不是中心对称图形,所以不符合题意.
因此选:A.
3、【答案】B
【解析】解:,
因此选:B
4、【答案】D
【解析】解:,所以A不符合题意;
,所以B不符合题意;
,所以C不符合题意;
,运算正确,所以D符合题意;
因此选:D
5、【答案】B
【解析】解:如图,∵,
∴,
∵,
∴,
因此选:B.
6、【答案】A
【解析】解:,
解①得:,
解②得:,
所以不等式组的解集为:,
在数轴上表示如下:
,
因此选:A
7、【答案】C
【解析】解:∵有数字4,5,6的三张卡片,将这三张卡片任意摆成一个三位数,
∴摆出的三位数有共6种可能,其中是
∴摆出的三位数是5的倍数的概率是,
因此选:C.
8、【答案】D
【解析】解:∵经过,
∴解析式为,
设正方形的边长为x,则点,
∴,
解得(舍去),
故点,
因此选:D.
9、【答案】D
【解析】解:A.根据,,不能判断四边形为平形四边形,所以该选项不正确,不符合题意;
B. ∵,∴,不能判断四边形为平形四边形,所以该选项不正确,不符合题意;
C.根据,,不能判断四边形为平形四边形,所以该选项不正确,不符合题意;
D.∵,
∴,
∵
∴,
∴
∴四边形为平形四边形,
所以该选项正确,符合题意;
因此选:D.
10、【答案】B
【解析】解:∵抛物线(a是常数,,
∴,
所以①正确;
当时,,
∴点在抛物线上,
所以②正确;
当时,,
当时,,
所以③错误;
根据对称点的坐标得到,
,
所以④错误.
因此选:B.
填空题
11、【答案】2
【解析】解:,8的立方根是2,
因此答案为:2.
12、【答案】3(a+b)2
【解析】解:3a2+6ab+3b2=3(a2+2ab+b2)=3(a+b)2.
因此答案为:3(a+b)2.
13、【答案】
【解析】解:去分母得:,
解得:,
经检验是方程的解,
因此答案为:.
14、【答案】分
【解析】解:根据题意得,跑步占,花样跳绳占,跳绳占考评,
则小红的最终得分为(分),
因此答案为:分.
15、【答案】
【解析】解:∵与相切于点,
∴,
∵,
∴,
∵,
∴,
∴,
因此答案为:
16、【答案】
【解析】解:帽子底面圆周长为:,
则扇形弧长为, 扇形面积
因此答案为:
17、【答案】
【解析】解:设这两年绿化面积的年平均增长率为,依题意,列方程为,
因此答案为:.
18、【答案】##
【解析】解:∵在矩形中,,
∴,,
如图,当点在上时,
∵
∴在为圆心,为半径的弧上运动,
当三点共线时,最短,
此时,
当点在上时,如图,
此时
当在上时,如图所示,此时
综上可知,的最小值为,
因此答案为:.
解答题
19、【答案】5
【解析】解:
.
20、【答案】,24
【解析】解:
当时,
原式
.
21、【答案】(1)见解析 (2)
【解析】(1)证明:∵,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
解得:.
22、【答案】(1)该公司销售一台甲型、一台乙型自行车的利润分别为元
(2)最少需要购买甲型自行车台
【解析】解:(1)该公司销售一台甲型、一台乙型自行车的利润分别为元,由题意得,
,
解得:,
答:该公司销售一台甲型、一台乙型自行车的利润分别为元;
(2)设需要购买甲型自行车台,则购买乙型自行车台,由题意得,
,
解得:,
因为为正整数,
所以的最小值为,
答:最少需要购买甲型自行车台.
23、【答案】(1)的值为,的值为.
(2)见解析. (3)16000
【解析】解:(1)样本容量:,
则,
故的值为,的值为.
(2)补全条形统计图如下:
(3)(名)
答:该市约有名九年级学生可以评为“A”级.
24、【答案】火箭从到处的平均速度为
【解析】解:根据题意,得,,,,
在中,,
,
在中,,
因为,
所以火箭从到处的平均速度为,
答:火箭从到处的平均速度为.
25、【答案】(1)见解析 (2)
【解析】(1)证明:∵等边三角形,
∴,,
∵,
∴,
∵绕点逆时针方向旋转,得到,
∴,
∴时等边三角形,
∴,
∴,
∴四点共圆,
∴,
∴.
(2)解:如图所示,根据题意得,只有当时,成立,
∵绕点逆时针方向旋转,得到,
∴,
∴时等边三角形,
∴,
∵,
∴,
∵等边三角形,
∴,
∵,
∴,
∴,
∴.
26、【答案】(1)
(2)
(3)点为或或或或
【解析】解:(1)∵抛物线经过点和点,
∴,
解得:,
∴抛物线解析式为:;
(2)∵抛物线与直线交于两点,(点在点的右侧)
联立,
解得:或,
∴,
∴,
∵点为直线上的一动点,设点的横坐标为.
则,,
∴,当时,取得最大值为,
∵,
∴当取得最大值时,最大,
∴,
∴面积的最大值;
(3)∵抛物线与轴交于点,
∴,当时,,即,
∵,
∴,
,,
①当为对角线时,如图,,
∴,
解得:,
∴,
∵的中点重合,
∴,
解得:,
∴,
②当为边时,如图,
当四边形为菱形,
∴,
解得:或,
∴或,
∴或,
由的中点重合,
∴或,
解得:或,
∴或,
当时;
如图,即四边形是菱形,
点的坐标即为四边形为菱形时,的坐标,
∴点为或,
综上所述,点为或或或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖南省邵阳市数学中考真题名师详解版
温馨提示:
(1)本学科试卷分试题卷和答题卡两部分,考试时量为120分钟,满分120分.
(2)请你将姓名、准考证号等相关信息按要求填涂在答题卡上.
(3)请在答题卡上作答,做在本试题卷上的答案无效.
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个项是符合题目要求的)
1. 的倒数是( )
A. B. C. D.
2. 下列四个图形中,是中心对称图形的是( )
A. B. C. D.
3. 党的二十大报告提出,要坚持以文塑旅、以旅彰文,推进文化和旅游深度融合发展.湖南是文化旅游资源大省,深挖红色文化、非遗文化和乡村文化,推进文旅产业赋能乡村振兴.湖南红色旅游区(点)2022年接待游客约165000000人次,则165000000用科学记数法可表示为( )
A. B. C. D.
4. 下列计算正确的是( )
A. B. C. D.
5. 如图,直线被直线所截,已知,则的大小为( )
A. B. C. D.
6. 不等式组的解集在数轴上可表示为( )
A. B.
C. D.
7. 有数字4,5,6的三张卡片,将这三张卡片任意摆成一个三位数,摆出的三位数是5的倍数的概率是( )
A. B. C. D.
8. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为,则点的坐标为( )
A. B. C. D.
9. 如图,在四边形中, ,若添加一个条件,使四边形为平形四边形,则下列正确的是( )
A. B. C. D.
10. 已知是抛物线(a是常数,上的点,现有以下四个结论:①该抛物线的对称轴是直线;②点在抛物线上;③若,则;④若,则其中,正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题有8个小题,每小题3分,共24分)
11. 的立方根是___________.
12. 分解因式:3a2+6ab+3b2=________________.
13. 分式方程的解是_____.
14. 下表是小红参加一次“阳光体育”活动比赛得分情况:
项目 跑步 花样跳绳 跳绳
得分 90 80 70
评总分时,按跑步占,花样跳绳占,跳绳占考评,则小红的最终得分为__________.
15. 如图,是的直径,是的弦,与相切于点,连接,若,则的大小为__________.
16. 如图,某数学兴趣小组用一张半径为的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为,那么这张扇形纸板的面积为__________.(结果保留)
17. 某校截止到年底,校园绿化面积为平方米.为美化环境,该校计划年底绿化面积达到平方米.利用方程想想,设这两年绿化面积的年平均增长率为,则依题意列方程为__________.
18. 如图,在矩形中,,动点在矩形边上沿运动.当点不与点重合时,将沿对折,得到,连接,则在点的运动过程中,线段的最小值为__________.
三、解答题(本大题有8个小题,第19-25题每题8分,第26题10分,共56分,解答应写出必要的文字说明、演算步骤或证明过程)
19. 计算:.
20. 先化简,再求值:,其中.
21. 如图,,点是线段上的一点,且.已知.
(1)证明:.
(2)求线段的长.
22. 低碳生活已是如今社会的一种潮流形式,人们的环保观念也在逐渐加深.低碳环保,绿色出行成为大家的生活理念,不少人选择自行车出行.某公司销售甲、乙两种型号的自行车,其中甲型自行车进货价格为每台元,乙型自行车进货价格为每台元.该公司销售台甲型自行车和台乙型自行车,可获利元,销售台甲型自行车和台乙型自行车,可获利元.
(1)该公司销售一台甲型、一台乙型自行车的利润各是多少元?
(2)为满足大众需求,该公司准备加购甲、乙两种型号的自行车共台,且资金不超过元,最少需要购买甲型自行车多少台?
23. 某市对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中随机抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出了如下频数分布图和如图(八)所示的条形统计图(不完整).请根据图表中的信息回答下列问题.
等级 频数 频率
A a 02
B 1600 b
C 1400 0.35
D 200 0.05
(1)求频数分布表中a,b的值.
(2)补全条形统计图.
(3)该市九年级学生约人,试估计该市有多少名九年级学生可以评为“A”级.
24. 我国航天事业捷报频传,2023年5月30日,被誉为“神箭”长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹中国空间站应用与发展阶段首次载人发射任务取得圆满成功,如图(九),有一枚运载火箭从地面处发射,当火箭到达处时,地面处的雷达站测得距离是,仰角为.,火箭直线到达处,此时地面处雷达站测得处的仰角为.求火箭从到处的平均速度(结果精确到).(参考数据:)
25. 如图,在等边三角形中,为上的一点,过点作的平行线交于点,点是线段上的动点(点不与重合).将绕点逆时针方向旋转,得到,连接交于.
(1)证明:在点的运动过程中,总有.
(2)当为何值时,是直角三角形?
26. 如图,在平面直角坐标系中,抛物线经过点和点,且与直线交于两点(点在点的右侧),点为直线上的一动点,设点的横坐标为.
(1)求抛物线的解析式.
(2)过点作轴垂线,与拋物线交于点.若,求面积的最大值.
(3)抛物线与轴交于点,点为平面直角坐标系上一点,若以为顶点的四边形是菱形,请求出所有满足条件的点的坐标.
参考答案及解析
一、选择题
1、【答案】C
【解析】解:的倒数为.
因此选:C.
2、【答案】A
【解析】解:A选项,是中心对称图形,所以符合题意;
B选项,不是中心对称图形,所以不符合题意;
C选项,不是中心对称图形,所以不符合题意;
D选项,不是中心对称图形,所以不符合题意.
因此选:A.
3、【答案】B
【解析】解:,
因此选:B
4、【答案】D
【解析】解:,所以A不符合题意;
,所以B不符合题意;
,所以C不符合题意;
,运算正确,所以D符合题意;
因此选:D
5、【答案】B
【解析】解:如图,∵,
∴,
∵,
∴,
因此选:B.
6、【答案】A
【解析】解:,
解①得:,
解②得:,
所以不等式组的解集为:,
在数轴上表示如下:
,
因此选:A
7、【答案】C
【解析】解:∵有数字4,5,6的三张卡片,将这三张卡片任意摆成一个三位数,
∴摆出的三位数有共6种可能,其中是
∴摆出的三位数是5的倍数的概率是,
因此选:C.
8、【答案】D
【解析】解:∵经过,
∴解析式为,
设正方形的边长为x,则点,
∴,
解得(舍去),
故点,
因此选:D.
9、【答案】D
【解析】解:A.根据,,不能判断四边形为平形四边形,所以该选项不正确,不符合题意;
B. ∵,∴,不能判断四边形为平形四边形,所以该选项不正确,不符合题意;
C.根据,,不能判断四边形为平形四边形,所以该选项不正确,不符合题意;
D.∵,
∴,
∵
∴,
∴
∴四边形为平形四边形,
所以该选项正确,符合题意;
因此选:D.
10、【答案】B
【解析】解:∵抛物线(a是常数,,
∴,
所以①正确;
当时,,
∴点在抛物线上,
所以②正确;
当时,,
当时,,
所以③错误;
根据对称点的坐标得到,
,
所以④错误.
因此选:B.
填空题
11、【答案】2
【解析】解:,8的立方根是2,
因此答案为:2.
12、【答案】3(a+b)2
【解析】解:3a2+6ab+3b2=3(a2+2ab+b2)=3(a+b)2.
因此答案为:3(a+b)2.
13、【答案】
【解析】解:去分母得:,
解得:,
经检验是方程的解,
因此答案为:.
14、【答案】分
【解析】解:根据题意得,跑步占,花样跳绳占,跳绳占考评,
则小红的最终得分为(分),
因此答案为:分.
15、【答案】
【解析】解:∵与相切于点,
∴,
∵,
∴,
∵,
∴,
∴,
因此答案为:
16、【答案】
【解析】解:帽子底面圆周长为:,
则扇形弧长为, 扇形面积
因此答案为:
17、【答案】
【解析】解:设这两年绿化面积的年平均增长率为,依题意,列方程为,
因此答案为:.
18、【答案】##
【解析】解:∵在矩形中,,
∴,,
如图,当点在上时,
∵
∴在为圆心,为半径的弧上运动,
当三点共线时,最短,
此时,
当点在上时,如图,
此时
当在上时,如图所示,此时
综上可知,的最小值为,
因此答案为:.
解答题
19、【答案】5
【解析】解:
.
20、【答案】,24
【解析】解:
当时,
原式
.
21、【答案】(1)见解析 (2)
【解析】(1)证明:∵,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
解得:.
22、【答案】(1)该公司销售一台甲型、一台乙型自行车的利润分别为元
(2)最少需要购买甲型自行车台
【解析】解:(1)该公司销售一台甲型、一台乙型自行车的利润分别为元,由题意得,
,
解得:,
答:该公司销售一台甲型、一台乙型自行车的利润分别为元;
(2)设需要购买甲型自行车台,则购买乙型自行车台,由题意得,
,
解得:,
因为为正整数,
所以的最小值为,
答:最少需要购买甲型自行车台.
23、【答案】(1)的值为,的值为.
(2)见解析. (3)16000
【解析】解:(1)样本容量:,
则,
故的值为,的值为.
(2)补全条形统计图如下:
(3)(名)
答:该市约有名九年级学生可以评为“A”级.
24、【答案】火箭从到处的平均速度为
【解析】解:根据题意,得,,,,
在中,,
,
在中,,
因为,
所以火箭从到处的平均速度为,
答:火箭从到处的平均速度为.
25、【答案】(1)见解析 (2)
【解析】(1)证明:∵等边三角形,
∴,,
∵,
∴,
∵绕点逆时针方向旋转,得到,
∴,
∴时等边三角形,
∴,
∴,
∴四点共圆,
∴,
∴.
(2)解:如图所示,根据题意得,只有当时,成立,
∵绕点逆时针方向旋转,得到,
∴,
∴时等边三角形,
∴,
∵,
∴,
∵等边三角形,
∴,
∵,
∴,
∴,
∴.
26、【答案】(1)
(2)
(3)点为或或或或
【解析】解:(1)∵抛物线经过点和点,
∴,
解得:,
∴抛物线解析式为:;
(2)∵抛物线与直线交于两点,(点在点的右侧)
联立,
解得:或,
∴,
∴,
∵点为直线上的一动点,设点的横坐标为.
则,,
∴,当时,取得最大值为,
∵,
∴当取得最大值时,最大,
∴,
∴面积的最大值;
(3)∵抛物线与轴交于点,
∴,当时,,即,
∵,
∴,
,,
①当为对角线时,如图,,
∴,
解得:,
∴,
∵的中点重合,
∴,
解得:,
∴,
②当为边时,如图,
当四边形为菱形,
∴,
解得:或,
∴或,
∴或,
由的中点重合,
∴或,
解得:或,
∴或,
当时;
如图,即四边形是菱形,
点的坐标即为四边形为菱形时,的坐标,
∴点为或,
综上所述,点为或或或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
