2023年湖南省益阳市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖南省益阳市数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年湖南省益阳市数学中考真题名师详解版
考生注意:
1.本学科试卷分试题卷和答题卡两部分;
2.请将姓名、准考证号等相关信息按要求填写在答题卡上;
3.请按答题卡上的注意事项在答题卡上作答,答在试题卷上无效;
4.本学科为闭卷考试,考试时量为120分钟,卷面满分为150分;
5.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本题共10个小题,每小题4分,共40分)
1. 四个实数,0,2,中,最大的数是( )
A. B. 0 C. 2 D.
2. 下列计算正确是( )
A. B. C. D.
3. 下列正方体的展开图中,是轴对称图形的是( )
A. B. C. D.
4. 将不等式组的解集在数轴上表示,正确的是( )
A B.
C D.
5. 某学校为进一步开展好劳动教育实践活动,用1580元购进A,B两种劳动工具共145件,A,B两种劳动工具每件分别为10元,12元.设购买A,B两种劳动工具的件数分别为x,y,那么下面列出的方程组中正确的是( )
A. B.
C. D.
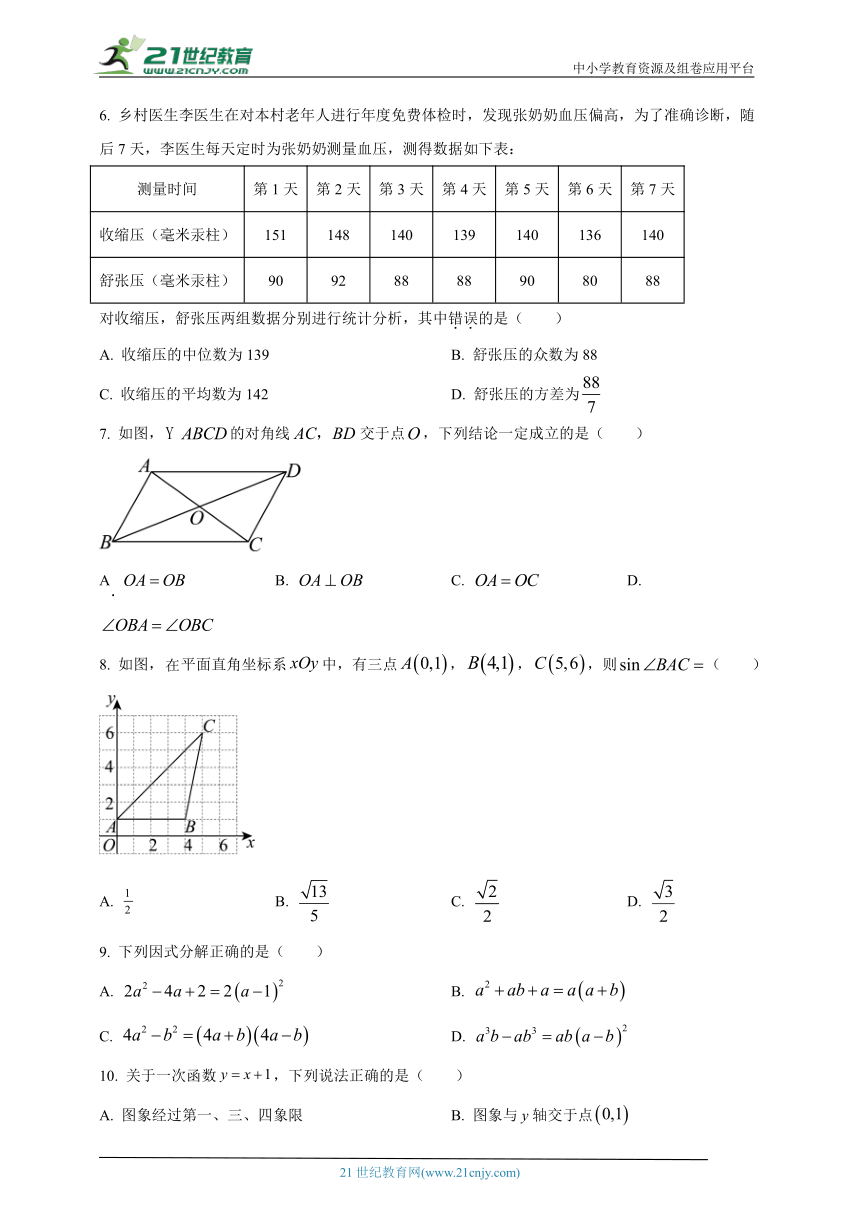
6. 乡村医生李医生在对本村老年人进行年度免费体检时,发现张奶奶血压偏高,为了准确诊断,随后7天,李医生每天定时为张奶奶测量血压,测得数据如下表:
测量时间 第1天 第2天 第3天 第4天 第5天 第6天 第7天
收缩压(毫米汞柱) 151 148 140 139 140 136 140
舒张压(毫米汞柱) 90 92 88 88 90 80 88
对收缩压,舒张压两组数据分别进行统计分析,其中错误的是( )
A. 收缩压的中位数为139 B. 舒张压的众数为88
C. 收缩压的平均数为142 D. 舒张压的方差为
7. 如图,的对角线交于点,下列结论一定成立的是( )
A B. C. D.
8. 如图,平面直角坐标系中,有三点,,,则( )
A. B. C. D.
9. 下列因式分解正确的是( )
A. B.
C. D.
10. 关于一次函数,下列说法正确的是( )
A. 图象经过第一、三、四象限 B. 图象与y轴交于点
C. 函数值y随自变量x的增大而减小 D. 当时,
二、填空题(本题共8个小题,每小题4分,共32分)
11. 据报道,2023年我国新能源汽车发展优势不断巩固和扩大,一季度全国新能源汽车销量为159万辆,同比增长.将1590000用科学记数法表示为______.
12. 计算:_______.
13. 从这10个整数中随机抽取1个数,抽到3的倍数的概率是______.
14. 分式方程的解是______.
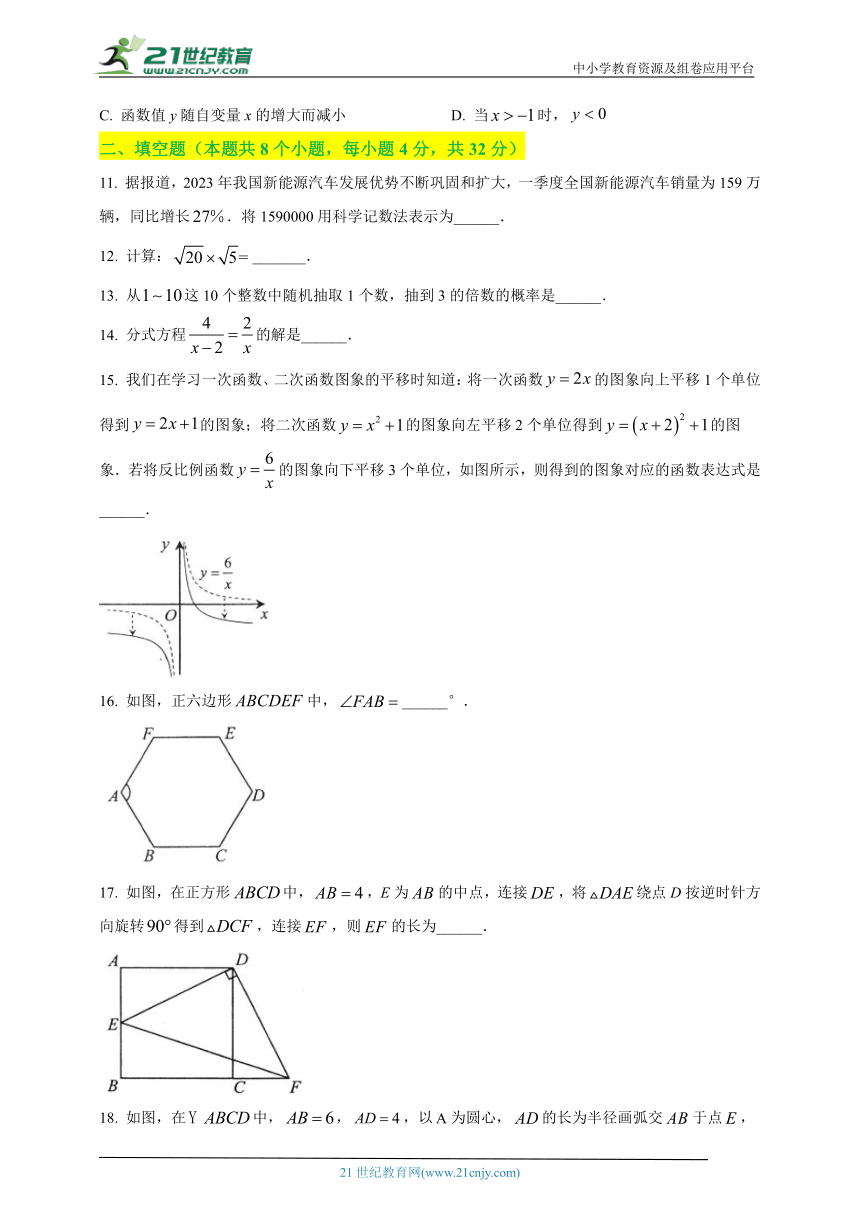
15. 我们在学习一次函数、二次函数图象的平移时知道:将一次函数的图象向上平移1个单位得到的图象;将二次函数的图象向左平移2个单位得到的图象.若将反比例函数的图象向下平移3个单位,如图所示,则得到的图象对应的函数表达式是______.
16. 如图,正六边形中,______°.
17. 如图,在正方形中,,E为的中点,连接,将绕点D按逆时针方向旋转得到,连接,则的长为______.
18. 如图,在中,,,以为圆心,的长为半径画弧交于点,连接,分别以为圆心,以大于的长为半径画弧,两弧交于点,作射线,交于点,过点作交于点.则的长为______.
三、解答题(本题共8个小题,共78分)
19. 计算:.
20. 如图,,直线与分别交于点E,F,上有一点G且,.求的度数.
21. 先化简,再求值:,其中.
22. 我市教育局为深入贯彻落实立德树人根本任务,2022年在全市中小学部署开展“六个一”德育行动.某校为了更好地开展此项活动,随机抽取部分学生对学校前段时间开展活动的情况进行了满意度调查,满意度分为四个等级:A:非常满意;B:满意;C:一般;D:不满意.根据调查数据绘制了如下两幅不完整的统计图表:
等级 人数
A 72
B 108
C 48
D m
请你根据图表中的信息,解答下列问题:
(1)本次被调查的学生人数是多少?
(2)求以上图表中m,n的值及扇形统计图中A等级对应的圆心角度数;
(3)若该校共有学生1200人,估计满意度为A,B等级的学生共有多少人?
23. 如图,线段与相切于点B,交于点M,其延长线交于点C,连接,,D为上一点且的中点为M,连接,.
(1)求的度数;
(2)四边形是否是菱形?如果是,请证明:如果不是,请说明理由;
(3)若,求的长.
24. 某企业准备对A,B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,投资B项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:.
(1)若将10万元资金投入A项目,一年后获得的收益是多少?
(2)若对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,则m的值是多少?
(3)2023年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A,B两个项目中,当A,B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?
25. 如图,在中,,,点D在边上,将线段绕点D按顺时针方向旋转得到,线段交于点E,作于点F,与线段交于点G,连接.
(1)求证:;
(2)求证:;
(3)若,,当平分四边形的面积时,求的长.
26. 在平面直角坐标系中,直线()与x轴交于点A,与抛物线交于B,C两点(B在C的左边).
(1)求A点的坐标;
(2)如图1,若B点关于x轴的对称点为点,当以点A,,C为顶点的三角形是直角三角形时,求实数a的值;
(3)定义:将平面直角坐标系中横坐标与纵坐标均为整数的点叫作格点,如,等均为格点.如图2,直线l与抛物线E所围成的封闭图形即阴影部分(不包含边界)中的格点数恰好是26个,求a的取值范围.
参考答案及解析
一、选择题
1、【答案】C
【解析】解:因为,
所以最大的数是2.
因此选:C
2、【答案】D
【解析】解:,所以A项不符合题意;
,所以B项不符合题意;
,所以C项不符合题意;
,所以D项符合题意;
因此选:D
3、【答案】D
【解析】解:由轴对称图形定义可知,A,B,C不能找到这样的一条直线使图形沿着这条直线对折后两部分完全重合,故不是轴对称图形;
D选项中的图形能找到这样的一条直线使图形沿着这条直线对折后两部分完全重合,是轴对称图形,
因此选:D.
4、【答案】B
【解析】解:,
解② 得:,
在数轴上表示两个不等式解集如下:
,
所以不等式组的解集为:;
因此选:B
5、【答案】A
【解析】解:设购买A,B两种劳动工具的件数分别为x,y,由题意得:
.
因此选:A
6、【答案】A
【解析】解:把收缩压的数据按照从小到大的顺序排列为:
136,139,140,140,140,148,151;
∴排在最中间的数据是140,可得中位数为140,所以A符合题意;
收缩压的平均数为:,所以C不符合题意;
舒张压的数据中88出现3次,所以舒张压的数据的众数为88,所以B不符合题意;
舒张压的平均数为:,
∴舒张压的方差为:;所以D不符合题意;
因此选:A
7、【答案】C
【解析】解:A、根据平行四边形性质:对角线相互平分,在中,,,则不一定成立,该项不符合题意;
B、根据平行四边形性质:对角线相互平分,不一定垂直,则不一定成立,该项不符合题意;
C、根据平行四边形性质:对角线相互平分,在中,,该项符合题意;
D、根据平行四边形性质,对角线不一定平分对角,则不一定成立,该项不符合题意;
因此选:C.
8、【答案】C
【解析】解:如图所示,取格点D,连接,,则点B在上,
∵,,,
∴,,,
∴,
∴;
因此选:C
9、【答案】A
【解析】解:A、,所以该选项正确,符合题意;
B、,所以该选项错误,不符合题意;
C、,所以该选项错误,不符合题意;
D、,所以该选项错误,不符合题意;
因此选:A
10、【答案】B
【解析】解:根据题意得:,
∴一次函数经过一、二、三象限,函数值y随自变量x的增大而增大,所以A、C错;
当时,,
∴图象与y轴交于点,所以B正确;
当时,,
∵函数值y随自变量x的增大而增大,
∴当时,,所以D错误;
因此选:B.
填空题
11、【答案】
【解析】解:将1590000用科学记数法表示为.
因此答案为:
12、【答案】
【解析】解:.
因此答案为:.
13、【答案】##
【解析】解:依题意得:在中共有10个整数,3的倍数只有3,6,9,共3个,
∴随机抽取一个数,抽到3的倍数的概率是,
因此答案为:.
14、【答案】
【解析】解:去分母得:,
解得:,
检验:当时,,
所以原方程的解为.
因此答案为:
15、【答案】
【解析】解:将反比例函数的图象向下平移3个单位,可得平移后的解析式为:
,
因此答案为:.
16、【答案】##度
【解析】解:因为是正六边形,
所以正六边形的所有的内角都相等;
所以;
因此答案为:.
17、【答案】
【解析】解:∵是正方形,
∴,,
∴,
∵E为的中点,
∴,
∴,
由旋转得:,,
∴;
因此答案为:.
18、【答案】
【解析】解:根据题意得,,射线是的角平分线,
由等腰三角形“三线合一”得是边中点,
,
由平行线分线段成比例定理得到,即是边中点,
是梯形的中位线,
,
在中,,,则,
故因此为:.
解答题
19、【答案】
【解析】解:
.
20、【答案】
【解析】解:∵,
∴,
∴,
∵,
∴,
∴.
21、【答案】,
【解析】解:
;
当时,
原式.
22、【答案】(1)本次被调查的学生人数是240人;
(2),;图中A等级对应的圆心角度数为;
(3)该校共有学生1200人,估计满意度为A,B等级的学生共有人.
【解析】解:(1)∵(人),
∴本次被调查的学生人数是240人;
(2)由题意得:(人),
,
∴;
,
∴图中A等级对应的圆心角度数为;
(3)∵(人),
∴该校共有学生1200人,估计满意度为A,B等级的学生共有人.
23、【答案】(1)
(2)是菱形,证明见解析
(3)的长为.
【解析】解:(1)连接,如图,
∵线段与相切于点B,
∴,而,
∴,
∵,
∴;
(2)四边形是菱形,理由如下:
∵的中点为M,,
∴,即,而,
∴,
∴,
∵的中点为M,为直径,
∴,
∴,
∵,,
∴,
∴,
∴,
∴四边形是菱形.
(3)连接,,交于,如图,
∵,,
∴为等边三角形,
∴,
∴,
∵菱形,,
∴,,
∴,
∵,
∴,
∴,
∴,
,
∴的长为.
24、【答案】(1)4万元 (2)
(3)当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【解析】解:(1)∵投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,
当时,(万元);
(2)∵对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,
∴,
整理得:,
解得:,(不符合题意,舍去),
∴m的值为8.
(3)
设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,
∴
,
而,
∴当时,(万元);
∴当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
25、【答案】(1)见解析 (2)见解析
(3)
【解析】(1)证明:∵线段绕点D按顺时针方向旋转得到,
∴,
∴,
∵,即,
∴,
∵,
∴,
在和中,
∵, ,
∴;
(2)证明:∵,
∴点B,C,G,F四点共圆,
∴,,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
即;
(3)解:连接,如图,
∵,
∴,,
∵,,
∴,
∴,,
∴,
设,则,
∴,,,
∴,
∴,,
∵平分四边形的面积,
∴,
∴,
即,
解得:(负值舍去),
∴.
26、【答案】(1)
(2)
(3)
【解析】解:(1)对于直线,
当时,,
∴A点的坐标为;
联立得:,
解得: 或,
∵B在C的左边,
∴点,
∵B点关于x轴的对称点为点,
∴点,
∴,,,
∵,
∴,此时,
即,
解得:(负值舍去);
(3)如图所示,设直线与y轴交于点D,直线分别与直线l与抛物线E交于点F,E,
对于直线,
当时,,
∴点,
当时,,
∴点,
对于抛物线,
当时,,
∴点,
∴,
∵直线l与抛物线E所围成的封闭图形即阴影部分(不包含边界)中的格点数恰好是26个,
∴封闭图形即阴影部分(不包含边界)中在y轴上格点数恰好是13个,
∴,
解得:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖南省益阳市数学中考真题名师详解版
考生注意:
1.本学科试卷分试题卷和答题卡两部分;
2.请将姓名、准考证号等相关信息按要求填写在答题卡上;
3.请按答题卡上的注意事项在答题卡上作答,答在试题卷上无效;
4.本学科为闭卷考试,考试时量为120分钟,卷面满分为150分;
5.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本题共10个小题,每小题4分,共40分)
1. 四个实数,0,2,中,最大的数是( )
A. B. 0 C. 2 D.
2. 下列计算正确是( )
A. B. C. D.
3. 下列正方体的展开图中,是轴对称图形的是( )
A. B. C. D.
4. 将不等式组的解集在数轴上表示,正确的是( )
A B.
C D.
5. 某学校为进一步开展好劳动教育实践活动,用1580元购进A,B两种劳动工具共145件,A,B两种劳动工具每件分别为10元,12元.设购买A,B两种劳动工具的件数分别为x,y,那么下面列出的方程组中正确的是( )
A. B.
C. D.
6. 乡村医生李医生在对本村老年人进行年度免费体检时,发现张奶奶血压偏高,为了准确诊断,随后7天,李医生每天定时为张奶奶测量血压,测得数据如下表:
测量时间 第1天 第2天 第3天 第4天 第5天 第6天 第7天
收缩压(毫米汞柱) 151 148 140 139 140 136 140
舒张压(毫米汞柱) 90 92 88 88 90 80 88
对收缩压,舒张压两组数据分别进行统计分析,其中错误的是( )
A. 收缩压的中位数为139 B. 舒张压的众数为88
C. 收缩压的平均数为142 D. 舒张压的方差为
7. 如图,的对角线交于点,下列结论一定成立的是( )
A B. C. D.
8. 如图,平面直角坐标系中,有三点,,,则( )
A. B. C. D.
9. 下列因式分解正确的是( )
A. B.
C. D.
10. 关于一次函数,下列说法正确的是( )
A. 图象经过第一、三、四象限 B. 图象与y轴交于点
C. 函数值y随自变量x的增大而减小 D. 当时,
二、填空题(本题共8个小题,每小题4分,共32分)
11. 据报道,2023年我国新能源汽车发展优势不断巩固和扩大,一季度全国新能源汽车销量为159万辆,同比增长.将1590000用科学记数法表示为______.
12. 计算:_______.
13. 从这10个整数中随机抽取1个数,抽到3的倍数的概率是______.
14. 分式方程的解是______.
15. 我们在学习一次函数、二次函数图象的平移时知道:将一次函数的图象向上平移1个单位得到的图象;将二次函数的图象向左平移2个单位得到的图象.若将反比例函数的图象向下平移3个单位,如图所示,则得到的图象对应的函数表达式是______.
16. 如图,正六边形中,______°.
17. 如图,在正方形中,,E为的中点,连接,将绕点D按逆时针方向旋转得到,连接,则的长为______.
18. 如图,在中,,,以为圆心,的长为半径画弧交于点,连接,分别以为圆心,以大于的长为半径画弧,两弧交于点,作射线,交于点,过点作交于点.则的长为______.
三、解答题(本题共8个小题,共78分)
19. 计算:.
20. 如图,,直线与分别交于点E,F,上有一点G且,.求的度数.
21. 先化简,再求值:,其中.
22. 我市教育局为深入贯彻落实立德树人根本任务,2022年在全市中小学部署开展“六个一”德育行动.某校为了更好地开展此项活动,随机抽取部分学生对学校前段时间开展活动的情况进行了满意度调查,满意度分为四个等级:A:非常满意;B:满意;C:一般;D:不满意.根据调查数据绘制了如下两幅不完整的统计图表:
等级 人数
A 72
B 108
C 48
D m
请你根据图表中的信息,解答下列问题:
(1)本次被调查的学生人数是多少?
(2)求以上图表中m,n的值及扇形统计图中A等级对应的圆心角度数;
(3)若该校共有学生1200人,估计满意度为A,B等级的学生共有多少人?
23. 如图,线段与相切于点B,交于点M,其延长线交于点C,连接,,D为上一点且的中点为M,连接,.
(1)求的度数;
(2)四边形是否是菱形?如果是,请证明:如果不是,请说明理由;
(3)若,求的长.
24. 某企业准备对A,B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,投资B项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:.
(1)若将10万元资金投入A项目,一年后获得的收益是多少?
(2)若对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,则m的值是多少?
(3)2023年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A,B两个项目中,当A,B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?
25. 如图,在中,,,点D在边上,将线段绕点D按顺时针方向旋转得到,线段交于点E,作于点F,与线段交于点G,连接.
(1)求证:;
(2)求证:;
(3)若,,当平分四边形的面积时,求的长.
26. 在平面直角坐标系中,直线()与x轴交于点A,与抛物线交于B,C两点(B在C的左边).
(1)求A点的坐标;
(2)如图1,若B点关于x轴的对称点为点,当以点A,,C为顶点的三角形是直角三角形时,求实数a的值;
(3)定义:将平面直角坐标系中横坐标与纵坐标均为整数的点叫作格点,如,等均为格点.如图2,直线l与抛物线E所围成的封闭图形即阴影部分(不包含边界)中的格点数恰好是26个,求a的取值范围.
参考答案及解析
一、选择题
1、【答案】C
【解析】解:因为,
所以最大的数是2.
因此选:C
2、【答案】D
【解析】解:,所以A项不符合题意;
,所以B项不符合题意;
,所以C项不符合题意;
,所以D项符合题意;
因此选:D
3、【答案】D
【解析】解:由轴对称图形定义可知,A,B,C不能找到这样的一条直线使图形沿着这条直线对折后两部分完全重合,故不是轴对称图形;
D选项中的图形能找到这样的一条直线使图形沿着这条直线对折后两部分完全重合,是轴对称图形,
因此选:D.
4、【答案】B
【解析】解:,
解② 得:,
在数轴上表示两个不等式解集如下:
,
所以不等式组的解集为:;
因此选:B
5、【答案】A
【解析】解:设购买A,B两种劳动工具的件数分别为x,y,由题意得:
.
因此选:A
6、【答案】A
【解析】解:把收缩压的数据按照从小到大的顺序排列为:
136,139,140,140,140,148,151;
∴排在最中间的数据是140,可得中位数为140,所以A符合题意;
收缩压的平均数为:,所以C不符合题意;
舒张压的数据中88出现3次,所以舒张压的数据的众数为88,所以B不符合题意;
舒张压的平均数为:,
∴舒张压的方差为:;所以D不符合题意;
因此选:A
7、【答案】C
【解析】解:A、根据平行四边形性质:对角线相互平分,在中,,,则不一定成立,该项不符合题意;
B、根据平行四边形性质:对角线相互平分,不一定垂直,则不一定成立,该项不符合题意;
C、根据平行四边形性质:对角线相互平分,在中,,该项符合题意;
D、根据平行四边形性质,对角线不一定平分对角,则不一定成立,该项不符合题意;
因此选:C.
8、【答案】C
【解析】解:如图所示,取格点D,连接,,则点B在上,
∵,,,
∴,,,
∴,
∴;
因此选:C
9、【答案】A
【解析】解:A、,所以该选项正确,符合题意;
B、,所以该选项错误,不符合题意;
C、,所以该选项错误,不符合题意;
D、,所以该选项错误,不符合题意;
因此选:A
10、【答案】B
【解析】解:根据题意得:,
∴一次函数经过一、二、三象限,函数值y随自变量x的增大而增大,所以A、C错;
当时,,
∴图象与y轴交于点,所以B正确;
当时,,
∵函数值y随自变量x的增大而增大,
∴当时,,所以D错误;
因此选:B.
填空题
11、【答案】
【解析】解:将1590000用科学记数法表示为.
因此答案为:
12、【答案】
【解析】解:.
因此答案为:.
13、【答案】##
【解析】解:依题意得:在中共有10个整数,3的倍数只有3,6,9,共3个,
∴随机抽取一个数,抽到3的倍数的概率是,
因此答案为:.
14、【答案】
【解析】解:去分母得:,
解得:,
检验:当时,,
所以原方程的解为.
因此答案为:
15、【答案】
【解析】解:将反比例函数的图象向下平移3个单位,可得平移后的解析式为:
,
因此答案为:.
16、【答案】##度
【解析】解:因为是正六边形,
所以正六边形的所有的内角都相等;
所以;
因此答案为:.
17、【答案】
【解析】解:∵是正方形,
∴,,
∴,
∵E为的中点,
∴,
∴,
由旋转得:,,
∴;
因此答案为:.
18、【答案】
【解析】解:根据题意得,,射线是的角平分线,
由等腰三角形“三线合一”得是边中点,
,
由平行线分线段成比例定理得到,即是边中点,
是梯形的中位线,
,
在中,,,则,
故因此为:.
解答题
19、【答案】
【解析】解:
.
20、【答案】
【解析】解:∵,
∴,
∴,
∵,
∴,
∴.
21、【答案】,
【解析】解:
;
当时,
原式.
22、【答案】(1)本次被调查的学生人数是240人;
(2),;图中A等级对应的圆心角度数为;
(3)该校共有学生1200人,估计满意度为A,B等级的学生共有人.
【解析】解:(1)∵(人),
∴本次被调查的学生人数是240人;
(2)由题意得:(人),
,
∴;
,
∴图中A等级对应的圆心角度数为;
(3)∵(人),
∴该校共有学生1200人,估计满意度为A,B等级的学生共有人.
23、【答案】(1)
(2)是菱形,证明见解析
(3)的长为.
【解析】解:(1)连接,如图,
∵线段与相切于点B,
∴,而,
∴,
∵,
∴;
(2)四边形是菱形,理由如下:
∵的中点为M,,
∴,即,而,
∴,
∴,
∵的中点为M,为直径,
∴,
∴,
∵,,
∴,
∴,
∴,
∴四边形是菱形.
(3)连接,,交于,如图,
∵,,
∴为等边三角形,
∴,
∴,
∵菱形,,
∴,,
∴,
∵,
∴,
∴,
∴,
,
∴的长为.
24、【答案】(1)4万元 (2)
(3)当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
【解析】解:(1)∵投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为:,
当时,(万元);
(2)∵对A,B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,
∴,
整理得:,
解得:,(不符合题意,舍去),
∴m的值为8.
(3)
设投入到B项目的资金为万元,则投入到A项目的资金为万元,设总收益为y万元,
∴
,
而,
∴当时,(万元);
∴当A,B两个项目分别投入28万,4万元时,一年后获得的收益之和最大,最大值是16万元.
25、【答案】(1)见解析 (2)见解析
(3)
【解析】(1)证明:∵线段绕点D按顺时针方向旋转得到,
∴,
∴,
∵,即,
∴,
∵,
∴,
在和中,
∵, ,
∴;
(2)证明:∵,
∴点B,C,G,F四点共圆,
∴,,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
即;
(3)解:连接,如图,
∵,
∴,,
∵,,
∴,
∴,,
∴,
设,则,
∴,,,
∴,
∴,,
∵平分四边形的面积,
∴,
∴,
即,
解得:(负值舍去),
∴.
26、【答案】(1)
(2)
(3)
【解析】解:(1)对于直线,
当时,,
∴A点的坐标为;
联立得:,
解得: 或,
∵B在C的左边,
∴点,
∵B点关于x轴的对称点为点,
∴点,
∴,,,
∵,
∴,此时,
即,
解得:(负值舍去);
(3)如图所示,设直线与y轴交于点D,直线分别与直线l与抛物线E交于点F,E,
对于直线,
当时,,
∴点,
当时,,
∴点,
对于抛物线,
当时,,
∴点,
∴,
∵直线l与抛物线E所围成的封闭图形即阴影部分(不包含边界)中的格点数恰好是26个,
∴封闭图形即阴影部分(不包含边界)中在y轴上格点数恰好是13个,
∴,
解得:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
