2023年海南省数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年海南省数学中考真题名师详解版 试卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年海南省数学中考真题名师详解版
(全卷满分120分,考试时间100分钟)
一、选择题(本大题满分36分,每小题3分)
在下列各题的四个备选答案中,有且只有一个是正确的,请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑.
1. 如图,数轴上点A表示的数的相反数是( )
A. 1 B. 0 C. D.
2. 若代数式的值为7,则x等于( )
A 9 B. C. 5 D.
3. 共享开放机遇,共创美好生活.2023年4月10日至15日,第三届中国品博览会在海南省海口市举行,以“打造全球消费精品展示交易平台”为目标,进场观众超32万人次,数据用科学记数法表示为( )
A. B. C. D.
4. 如图是由5个完全相同的小正方体摆成的几何体,则这个几何体的俯视图是( )
A. B. C. D.
5. 下列计算中,正确的是( )
A. B. C. D.
6. 水是生命之源.为了倡导节约用水,随机抽取某小区7户家庭上个月家里的用水量情况(单位:吨),数据为:7,5,6,8,9,9,10.这组数据的中位数和众数分别是( )
A. 9,8 B. 9,9 C. 8.5,9 D. 8,9
7. 分式方程的解是( )
A. B. C. D.
8. 若反比例函数()的图象经过点,则k的值是( )
A. 2 B. C. D.
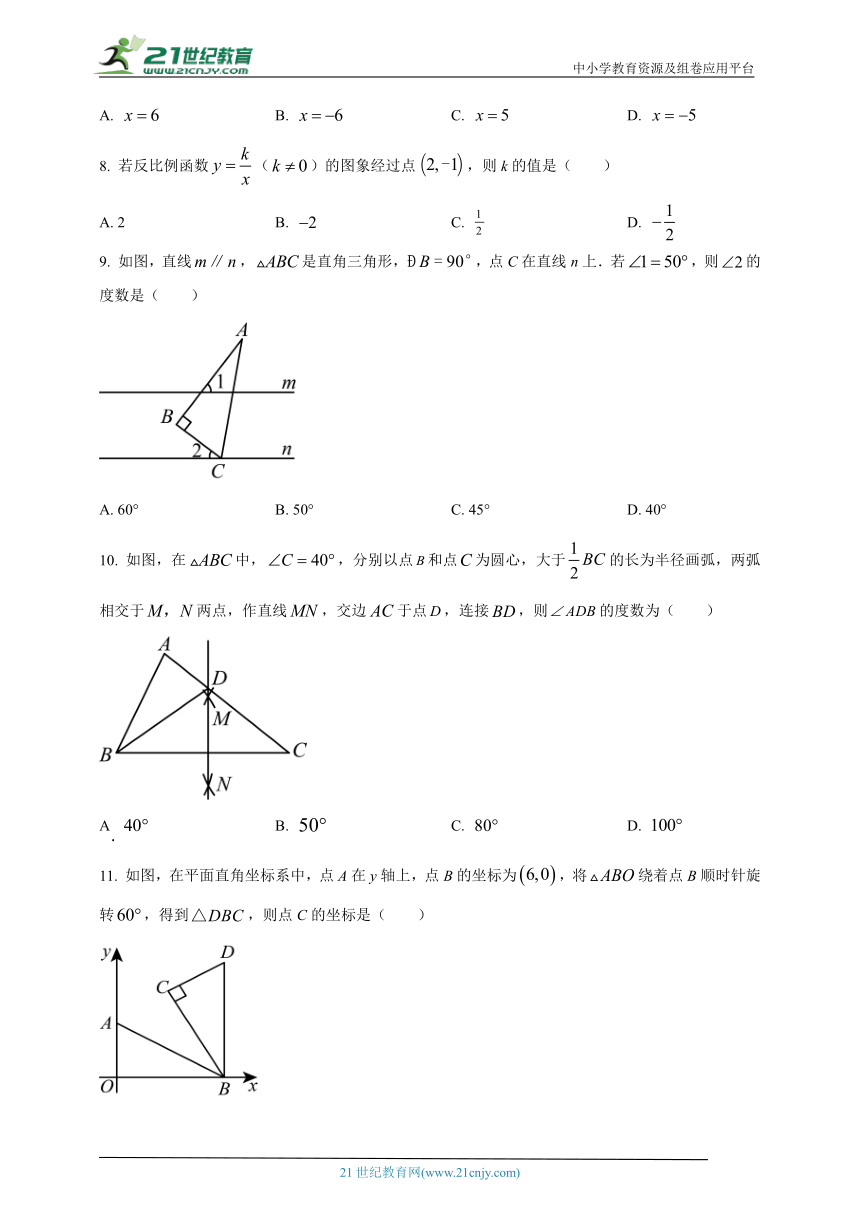
9. 如图,直线,是直角三角形,,点C在直线n上.若,则的度数是( )
A. 60° B. 50° C. 45° D. 40°
10. 如图,在中,,分别以点和点为圆心,大于的长为半径画弧,两弧相交于两点,作直线,交边于点,连接,则的度数为( )
A B. C. D.
11. 如图,在平面直角坐标系中,点A在y轴上,点B的坐标为,将绕着点B顺时针旋转,得到,则点C的坐标是( )
A. B. C. D.
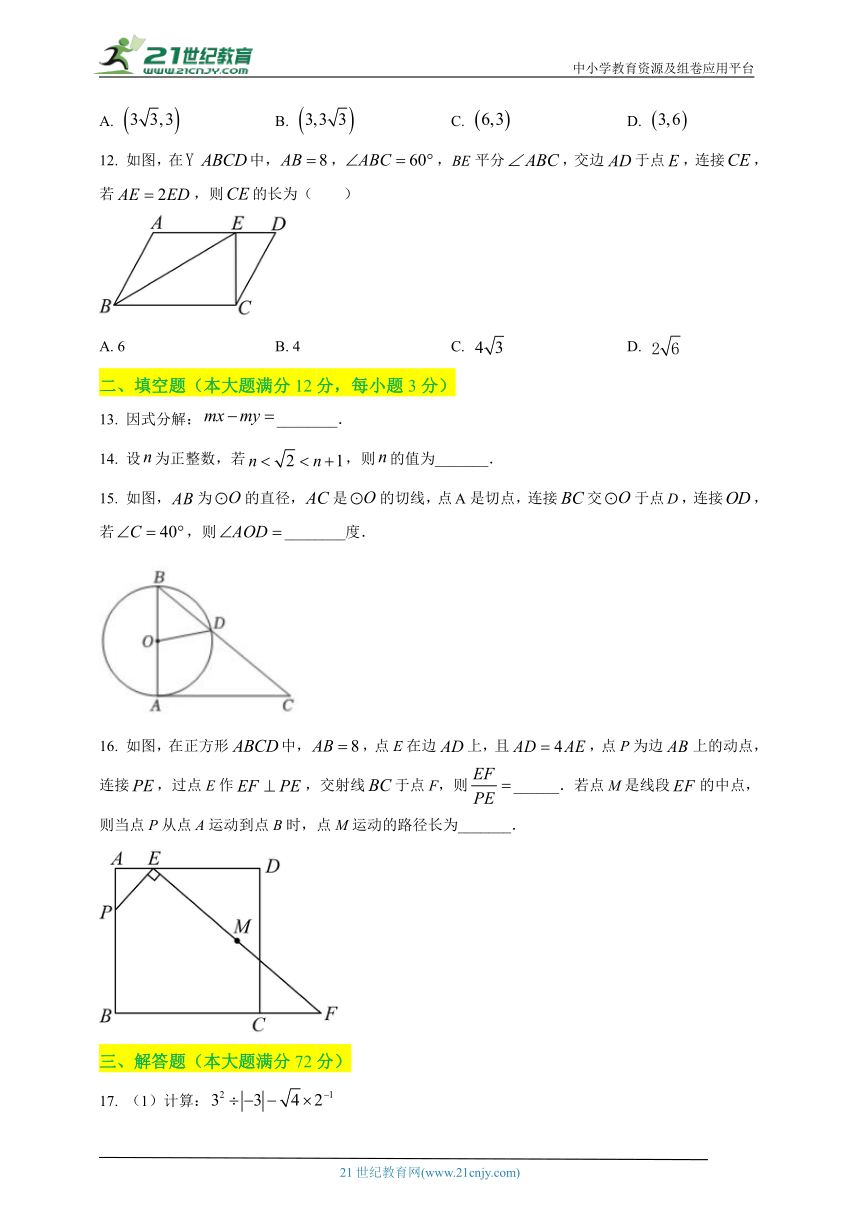
12. 如图,在中,,,平分,交边于点,连接,若,则的长为( )
A. 6 B. 4 C. D.
二、填空题(本大题满分12分,每小题3分)
13. 因式分解:________.
14. 设为正整数,若,则的值为_______.
15. 如图,为的直径,是的切线,点是切点,连接交于点,连接,若,则________度.
16. 如图,在正方形中,,点E在边上,且,点P为边上的动点,连接,过点E作,交射线于点F,则______.若点M是线段的中点,则当点P从点A运动到点B时,点M运动的路径长为_______.
三、解答题(本大题满分72分)
17. (1)计算:
(2)解不等式组:
18. 2023年5月10日,搭载天舟六号货运飞船的长征七号遥七运载火箭,在我国文昌航天发射场点火发射成功.为了普及航空航天科普知识,某校组织学生去文昌卫星发射中心参观学习.已知该校租用甲、乙两种不同型号的客车共15辆,租用1辆甲型客车需600元,1辆乙型客车需500元,租车费共8000元.问甲、乙两种型号客车各租多少辆?
19. 某中学为了了解学生最喜欢的课外活动,以便更好开展课后服务.随机抽取若干名学生进行了问卷调查.调查问卷如下:
调查问题 在下列课外活动中,你最喜欢的是( )(单选) A.文学;B.科技;C.艺术;D.体育 填完后,请将问卷交给教务处.
根据统计得到的数据,绘制成下面的两幅不完整的统计图.
请根据统计图提供信息,解答下面的问题:
(1)本次调查采用的调查方式为 (填写“普查”或“抽样调查”);
(2)在这次调查中,抽取的学生一共有 人;扇形统计图中的值为 ;
(3)已知选择“科技”类课外活动的50名学生中有30名男生和20名女生.若从这50名学生中随机抽取1名学生座谈,且每名学生被抽到的可能性相同,则恰好抽到女生的概率是 ;
(4)若该校共有1000名学生参加课外活动,则估计选择“文学”类课外活动的学生有 人.
20. 如图,一艘轮船在处测得灯塔位于的北偏东方向上,轮船沿着正北方向航行20海里到达处,测得灯塔位于的北偏东方向上,测得港口位于的北偏东方向上.已知港口在灯塔的正北方向上.
(1)填空: 度, 度;
(2)求灯塔到轮船航线距离(结果保留根号);
(3)求港口与灯塔的距离(结果保留根号).
21. 如图1,在菱形中,对角线,相交于点,,,点为线段上的动点(不与点,重合),连接并延长交边于点,交的延长线于点.
(1)当点恰好为的中点时,求证:;
(2)求线段的长;
(3)当为直角三角形时,求的值;
(4)如图2,作线段的垂直平分线,交于点,交于点,连接,在点的运动过程中,的度数是否为定值?如果是,求出这个定值;如果不是,请说明理由.
22. 如图1,抛物线交x轴于A,两点,交y轴于点.点P是抛物线上一动点.
(1)求该抛物线的函数表达式;
(2)当点P的坐标为时,求四边形的面积;
(3)当动点P在直线上方时,在平面直角坐标系是否存在点Q,使得以B,C,P,Q为顶点四边形是矩形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(4)如图2,点D是抛物线的顶点,过点D作直线轴,交x轴于点H,当点P在第二象限时,作直线,分别与直线交于点G和点I,求证:点D是线段的中点.
参考答案及解析
一、选择题
1、【答案】A
【解析】解:根据数轴可知,点A表示的数是,的相反数是.
因此选:A.
2、【答案】C
【解析】解:因为代数式的值等于7,
所以,
解得:,
因此选:C.
3、【答案】B
【解析】解:,
因此选:B.
4、【答案】C
【解析】解:由题意可知:
这个几何体的俯视图是: ,
因此选:C.
5、【答案】A
【解析】因为,
故A项正确;
因为,
故B项不正确;
因为,
故C项不正确;
因为,
故D项不正确.
因此选:A.
6、【答案】D
【解析】解:7,5,6,8,9,9,10中9出现次数最多,所以众数为9;
从小到大进行排序为5,6,7,8,9,9,10,中间位置的数是8,所以中位数是8.
因此选:D.
7、【答案】A
【解析】解:去分母得:,
解得:,
检验,当时,,
所以原分式方程的解是,
因此选:A.
8、【答案】B
【解析】解:因为反比例函数()的图象经过点,
所以,
解得:,
因此选:B
9、【答案】D
【解析】解:延长交直线n于点D,如图,
∵,
∴,
在中,.
因此选:D.
10、【答案】C
【解析】解:根据作图可知:是直线的垂直平分线,
,
,
,
因此选:C.
11、【答案】B
【解析】解:过点作,如图所示,
则
根据题意可得:,,
∴,
∴,
∴,,
∴点的坐标为,
因此选:B
12、【答案】C
【解析】解:四边形是平行四边形,
,,,
,
平分,
,
,
,
又,
,
过点作于点,如图所示,
,
则,
,
,
,
,
因此选:C.
填空题
13、【答案】
【解析】解:,
因此答案为:
14、【答案】1
【解析】解:,
,即:,
,
,
因此答案为:1.
15、【答案】100
【解析】解:是的切线,为的直径,
,
,
,
,
,
因此答案为:100.
16、【答案】 ①. ②.
【解析】解:过点作交延长线于点,如图所示,
则四边形为矩形,
∴,
根据题意可得:,
∵,
∴,
又∵,
∴,
∴,
∴,
过点作交于点,交于点,如图所示,
∵,,
∴,
在和中,
,
∴,
∴,
所以点的运动轨迹是一条平行于的线段,
当点与重合时,,
当点与重合时,,,
∴,
∵,
∴,
∴,即:,
解得:,
又∵、分别为、的中点,
∴是的中位线,
∴,即点运动的路径长为.
因此答案为:,.
解答题
17、【答案】(1);(2).
【解析】解:(1);
(2),
解不等式①得:,
解不等式②得:,
所以不等式组的解集为:.
18、【答案】甲型号客车租辆,乙型号客车租辆
【解析】解:设甲型号客车租辆,乙型号客车租辆,
由根据意得:,
解得:,
答:甲型号客车租辆,乙型号客车租辆.
19、【答案】(1)抽样调查
(2)200,22 (3)
(4)350
【解析】解:(1)由题意可得:
本次调查采用的调查方式为抽样调查,
因此答案为:抽样调查;
(2)由题意可得:
在这次调查中,抽取的学生一共有:(人),
扇形统计图中的值为:,
因此答案为:200,22;
(3)恰好抽到女生的概率为:,
因此答案为:;
(4)由题意可得,
选择“文学”类课外活动的学生有:(人),
因此答案为:350.
20、【答案】(1)30,45
(2)灯塔到轮船航线的距离为海里
(3)港口与灯塔距离为海里
【解析】解:(1)作交于,作交于,如图所示,
,
,
都是正北方向,
,
,
,
因此答案为:30,45;
(2)作交于,作交于,如图所示,
由(1)可得:,
海里,
在中,,海里,
海里;
灯塔到轮船航线的距离为海里;
(3)作交于,作交于,如图所示,
,,、都是正北方向,
四边形是矩形,
海里,,
在中,,海里,
海里,
在中,,
是等腰直角三角形,
海里,
海里,
港口与灯塔的距离为海里.
21、【答案】(1)见解析 (2)
(3)2或
(4)的度数是定值,
【解析】(1)证明:四边形是菱形,
,
,
点是的中点,
,
,
;
(2)解:四边形是菱形,,,
,,,,
,
,
,
,
(3)解:当时,
四边形是菱形,
,,,,
,
,即,
,,
,,
,
,
,
又,
,
,
;
当时,
,
由(2)可得:,,
四边形是菱形,
,
,
,
,
,
,
,
,
综上:或2,
(4)解:的度数是定值.
取中点,连接、、,如图所示,
是的垂直平分线,
,,
,
点是的中点,,
,
四边形是菱形,
,,,
点是的中点,,
,
点、点、点三点共线,
点是的中点,,
,
,
,
,
点、点、点、点四点共圆,
,
.
22、【答案】(1)
(2)9 (3)在平面直角坐标系内存在点Q,使得以B、C、P、Q为顶点的四边形是矩形,此时点Q的坐标为或
(4)证明过程见解析
【解析】(1)解:根据题意得,,
解得:,
所以抛物线的解析式为;
(2)解:如图所示,连接,过点P作于点E,
∵点P的坐标为,
∴,,
令,即:,
解得:或,
∴,
∴,
∵,,
∴,,
∴,
;
(3)解:在平面直角坐标系内存在点Q,使得以B、C、P、Q为顶点的四边形是矩形,理由:
如图所示,当为边时,四边形为符合条件的矩形,交y轴于点E,交x轴于点F,连接,过点P作轴于点M,过点Q作轴于点N,
∵,
∴,
∵四边形为矩形,
∴,
∴,
∴和为等腰直角三角形,
∴,
∵四边形为正方形,
∴,
∴四边形为矩形,
∴,
∵,
∴和为全等的等腰直角三角形,
∴,
∵,
∴,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
联立得,
解得或,
∴,
∴,
∴,
∴,
∴,
如图所示,当为对角线时,四边形为矩形,过点Q作轴于点D,轴于点E,
则,,
∵,
∴,
∴,
∴,
设点P的坐标为:,,
∵,,
∴,,
∴,
∴,,,,
∴,
整理得:,
分解因式得:,
解得:(舍去),(舍去),,
∴此时点Q的坐标为:.
综上所述,在平面直角坐标系内存在点Q,使得以B、C、P、Q为顶点的四边形是矩形,
此时点Q的坐标为或;
(4)证明:∵,
∴抛物线的顶点D的坐标为,对称轴为,
设,直线的解析式为,
∴,
∴,
∴直线的解析式为,
当时,,
∴,
∴,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
当时,,
∴,
∴,
∴,
∴点D是线段的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年海南省数学中考真题名师详解版
(全卷满分120分,考试时间100分钟)
一、选择题(本大题满分36分,每小题3分)
在下列各题的四个备选答案中,有且只有一个是正确的,请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑.
1. 如图,数轴上点A表示的数的相反数是( )
A. 1 B. 0 C. D.
2. 若代数式的值为7,则x等于( )
A 9 B. C. 5 D.
3. 共享开放机遇,共创美好生活.2023年4月10日至15日,第三届中国品博览会在海南省海口市举行,以“打造全球消费精品展示交易平台”为目标,进场观众超32万人次,数据用科学记数法表示为( )
A. B. C. D.
4. 如图是由5个完全相同的小正方体摆成的几何体,则这个几何体的俯视图是( )
A. B. C. D.
5. 下列计算中,正确的是( )
A. B. C. D.
6. 水是生命之源.为了倡导节约用水,随机抽取某小区7户家庭上个月家里的用水量情况(单位:吨),数据为:7,5,6,8,9,9,10.这组数据的中位数和众数分别是( )
A. 9,8 B. 9,9 C. 8.5,9 D. 8,9
7. 分式方程的解是( )
A. B. C. D.
8. 若反比例函数()的图象经过点,则k的值是( )
A. 2 B. C. D.
9. 如图,直线,是直角三角形,,点C在直线n上.若,则的度数是( )
A. 60° B. 50° C. 45° D. 40°
10. 如图,在中,,分别以点和点为圆心,大于的长为半径画弧,两弧相交于两点,作直线,交边于点,连接,则的度数为( )
A B. C. D.
11. 如图,在平面直角坐标系中,点A在y轴上,点B的坐标为,将绕着点B顺时针旋转,得到,则点C的坐标是( )
A. B. C. D.
12. 如图,在中,,,平分,交边于点,连接,若,则的长为( )
A. 6 B. 4 C. D.
二、填空题(本大题满分12分,每小题3分)
13. 因式分解:________.
14. 设为正整数,若,则的值为_______.
15. 如图,为的直径,是的切线,点是切点,连接交于点,连接,若,则________度.
16. 如图,在正方形中,,点E在边上,且,点P为边上的动点,连接,过点E作,交射线于点F,则______.若点M是线段的中点,则当点P从点A运动到点B时,点M运动的路径长为_______.
三、解答题(本大题满分72分)
17. (1)计算:
(2)解不等式组:
18. 2023年5月10日,搭载天舟六号货运飞船的长征七号遥七运载火箭,在我国文昌航天发射场点火发射成功.为了普及航空航天科普知识,某校组织学生去文昌卫星发射中心参观学习.已知该校租用甲、乙两种不同型号的客车共15辆,租用1辆甲型客车需600元,1辆乙型客车需500元,租车费共8000元.问甲、乙两种型号客车各租多少辆?
19. 某中学为了了解学生最喜欢的课外活动,以便更好开展课后服务.随机抽取若干名学生进行了问卷调查.调查问卷如下:
调查问题 在下列课外活动中,你最喜欢的是( )(单选) A.文学;B.科技;C.艺术;D.体育 填完后,请将问卷交给教务处.
根据统计得到的数据,绘制成下面的两幅不完整的统计图.
请根据统计图提供信息,解答下面的问题:
(1)本次调查采用的调查方式为 (填写“普查”或“抽样调查”);
(2)在这次调查中,抽取的学生一共有 人;扇形统计图中的值为 ;
(3)已知选择“科技”类课外活动的50名学生中有30名男生和20名女生.若从这50名学生中随机抽取1名学生座谈,且每名学生被抽到的可能性相同,则恰好抽到女生的概率是 ;
(4)若该校共有1000名学生参加课外活动,则估计选择“文学”类课外活动的学生有 人.
20. 如图,一艘轮船在处测得灯塔位于的北偏东方向上,轮船沿着正北方向航行20海里到达处,测得灯塔位于的北偏东方向上,测得港口位于的北偏东方向上.已知港口在灯塔的正北方向上.
(1)填空: 度, 度;
(2)求灯塔到轮船航线距离(结果保留根号);
(3)求港口与灯塔的距离(结果保留根号).
21. 如图1,在菱形中,对角线,相交于点,,,点为线段上的动点(不与点,重合),连接并延长交边于点,交的延长线于点.
(1)当点恰好为的中点时,求证:;
(2)求线段的长;
(3)当为直角三角形时,求的值;
(4)如图2,作线段的垂直平分线,交于点,交于点,连接,在点的运动过程中,的度数是否为定值?如果是,求出这个定值;如果不是,请说明理由.
22. 如图1,抛物线交x轴于A,两点,交y轴于点.点P是抛物线上一动点.
(1)求该抛物线的函数表达式;
(2)当点P的坐标为时,求四边形的面积;
(3)当动点P在直线上方时,在平面直角坐标系是否存在点Q,使得以B,C,P,Q为顶点四边形是矩形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(4)如图2,点D是抛物线的顶点,过点D作直线轴,交x轴于点H,当点P在第二象限时,作直线,分别与直线交于点G和点I,求证:点D是线段的中点.
参考答案及解析
一、选择题
1、【答案】A
【解析】解:根据数轴可知,点A表示的数是,的相反数是.
因此选:A.
2、【答案】C
【解析】解:因为代数式的值等于7,
所以,
解得:,
因此选:C.
3、【答案】B
【解析】解:,
因此选:B.
4、【答案】C
【解析】解:由题意可知:
这个几何体的俯视图是: ,
因此选:C.
5、【答案】A
【解析】因为,
故A项正确;
因为,
故B项不正确;
因为,
故C项不正确;
因为,
故D项不正确.
因此选:A.
6、【答案】D
【解析】解:7,5,6,8,9,9,10中9出现次数最多,所以众数为9;
从小到大进行排序为5,6,7,8,9,9,10,中间位置的数是8,所以中位数是8.
因此选:D.
7、【答案】A
【解析】解:去分母得:,
解得:,
检验,当时,,
所以原分式方程的解是,
因此选:A.
8、【答案】B
【解析】解:因为反比例函数()的图象经过点,
所以,
解得:,
因此选:B
9、【答案】D
【解析】解:延长交直线n于点D,如图,
∵,
∴,
在中,.
因此选:D.
10、【答案】C
【解析】解:根据作图可知:是直线的垂直平分线,
,
,
,
因此选:C.
11、【答案】B
【解析】解:过点作,如图所示,
则
根据题意可得:,,
∴,
∴,
∴,,
∴点的坐标为,
因此选:B
12、【答案】C
【解析】解:四边形是平行四边形,
,,,
,
平分,
,
,
,
又,
,
过点作于点,如图所示,
,
则,
,
,
,
,
因此选:C.
填空题
13、【答案】
【解析】解:,
因此答案为:
14、【答案】1
【解析】解:,
,即:,
,
,
因此答案为:1.
15、【答案】100
【解析】解:是的切线,为的直径,
,
,
,
,
,
因此答案为:100.
16、【答案】 ①. ②.
【解析】解:过点作交延长线于点,如图所示,
则四边形为矩形,
∴,
根据题意可得:,
∵,
∴,
又∵,
∴,
∴,
∴,
过点作交于点,交于点,如图所示,
∵,,
∴,
在和中,
,
∴,
∴,
所以点的运动轨迹是一条平行于的线段,
当点与重合时,,
当点与重合时,,,
∴,
∵,
∴,
∴,即:,
解得:,
又∵、分别为、的中点,
∴是的中位线,
∴,即点运动的路径长为.
因此答案为:,.
解答题
17、【答案】(1);(2).
【解析】解:(1);
(2),
解不等式①得:,
解不等式②得:,
所以不等式组的解集为:.
18、【答案】甲型号客车租辆,乙型号客车租辆
【解析】解:设甲型号客车租辆,乙型号客车租辆,
由根据意得:,
解得:,
答:甲型号客车租辆,乙型号客车租辆.
19、【答案】(1)抽样调查
(2)200,22 (3)
(4)350
【解析】解:(1)由题意可得:
本次调查采用的调查方式为抽样调查,
因此答案为:抽样调查;
(2)由题意可得:
在这次调查中,抽取的学生一共有:(人),
扇形统计图中的值为:,
因此答案为:200,22;
(3)恰好抽到女生的概率为:,
因此答案为:;
(4)由题意可得,
选择“文学”类课外活动的学生有:(人),
因此答案为:350.
20、【答案】(1)30,45
(2)灯塔到轮船航线的距离为海里
(3)港口与灯塔距离为海里
【解析】解:(1)作交于,作交于,如图所示,
,
,
都是正北方向,
,
,
,
因此答案为:30,45;
(2)作交于,作交于,如图所示,
由(1)可得:,
海里,
在中,,海里,
海里;
灯塔到轮船航线的距离为海里;
(3)作交于,作交于,如图所示,
,,、都是正北方向,
四边形是矩形,
海里,,
在中,,海里,
海里,
在中,,
是等腰直角三角形,
海里,
海里,
港口与灯塔的距离为海里.
21、【答案】(1)见解析 (2)
(3)2或
(4)的度数是定值,
【解析】(1)证明:四边形是菱形,
,
,
点是的中点,
,
,
;
(2)解:四边形是菱形,,,
,,,,
,
,
,
,
(3)解:当时,
四边形是菱形,
,,,,
,
,即,
,,
,,
,
,
,
又,
,
,
;
当时,
,
由(2)可得:,,
四边形是菱形,
,
,
,
,
,
,
,
,
综上:或2,
(4)解:的度数是定值.
取中点,连接、、,如图所示,
是的垂直平分线,
,,
,
点是的中点,,
,
四边形是菱形,
,,,
点是的中点,,
,
点、点、点三点共线,
点是的中点,,
,
,
,
,
点、点、点、点四点共圆,
,
.
22、【答案】(1)
(2)9 (3)在平面直角坐标系内存在点Q,使得以B、C、P、Q为顶点的四边形是矩形,此时点Q的坐标为或
(4)证明过程见解析
【解析】(1)解:根据题意得,,
解得:,
所以抛物线的解析式为;
(2)解:如图所示,连接,过点P作于点E,
∵点P的坐标为,
∴,,
令,即:,
解得:或,
∴,
∴,
∵,,
∴,,
∴,
;
(3)解:在平面直角坐标系内存在点Q,使得以B、C、P、Q为顶点的四边形是矩形,理由:
如图所示,当为边时,四边形为符合条件的矩形,交y轴于点E,交x轴于点F,连接,过点P作轴于点M,过点Q作轴于点N,
∵,
∴,
∵四边形为矩形,
∴,
∴,
∴和为等腰直角三角形,
∴,
∵四边形为正方形,
∴,
∴四边形为矩形,
∴,
∵,
∴和为全等的等腰直角三角形,
∴,
∵,
∴,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
联立得,
解得或,
∴,
∴,
∴,
∴,
∴,
如图所示,当为对角线时,四边形为矩形,过点Q作轴于点D,轴于点E,
则,,
∵,
∴,
∴,
∴,
设点P的坐标为:,,
∵,,
∴,,
∴,
∴,,,,
∴,
整理得:,
分解因式得:,
解得:(舍去),(舍去),,
∴此时点Q的坐标为:.
综上所述,在平面直角坐标系内存在点Q,使得以B、C、P、Q为顶点的四边形是矩形,
此时点Q的坐标为或;
(4)证明:∵,
∴抛物线的顶点D的坐标为,对称轴为,
设,直线的解析式为,
∴,
∴,
∴直线的解析式为,
当时,,
∴,
∴,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
当时,,
∴,
∴,
∴,
∴点D是线段的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
