2023年河南省数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年河南省数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023年河南省数学中考真题名师详解版
一、选择题
1. 下列各数中,最小的数是( )
A -l B. 0 C. 1 D.
2. 北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A 主视图与左视图相同 B. 主视图与俯视图相同
C. 左视图与俯视图相同 D. 三种视图都相同
3. 2022年河南省出版4.59亿册图书,为贯彻落实党的二十大关于深化全民阅读活动的重要精神,建设学习型社会提供了丰富的图书资源.数据“4.59亿”用科学记数法表示为( )
A. B. C. D.
4. 如图,直线,相交于点O,若,,则的度数为( )
A. B. C. D.
5. 化简的结果是( )
A. 0 B. 1 C. a D.
6. 如图,点A,B,C在上,若,则的度数为( )
A. B. C. D.
7. 关于x的一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
8. 为落实教育部办公厅、中共中央宣传部办公厅关于《第41批向全国中小学生推荐优秀影片片目》的通知精神,某校七、八年级分别从如图所示的三部影片中随机选择一部组织本年级学生观看,则这两个年级选择的影片相同的概率为( )
A. B. C. D.
9. 二次函数的图象如图所示,则一次函数的图象一定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
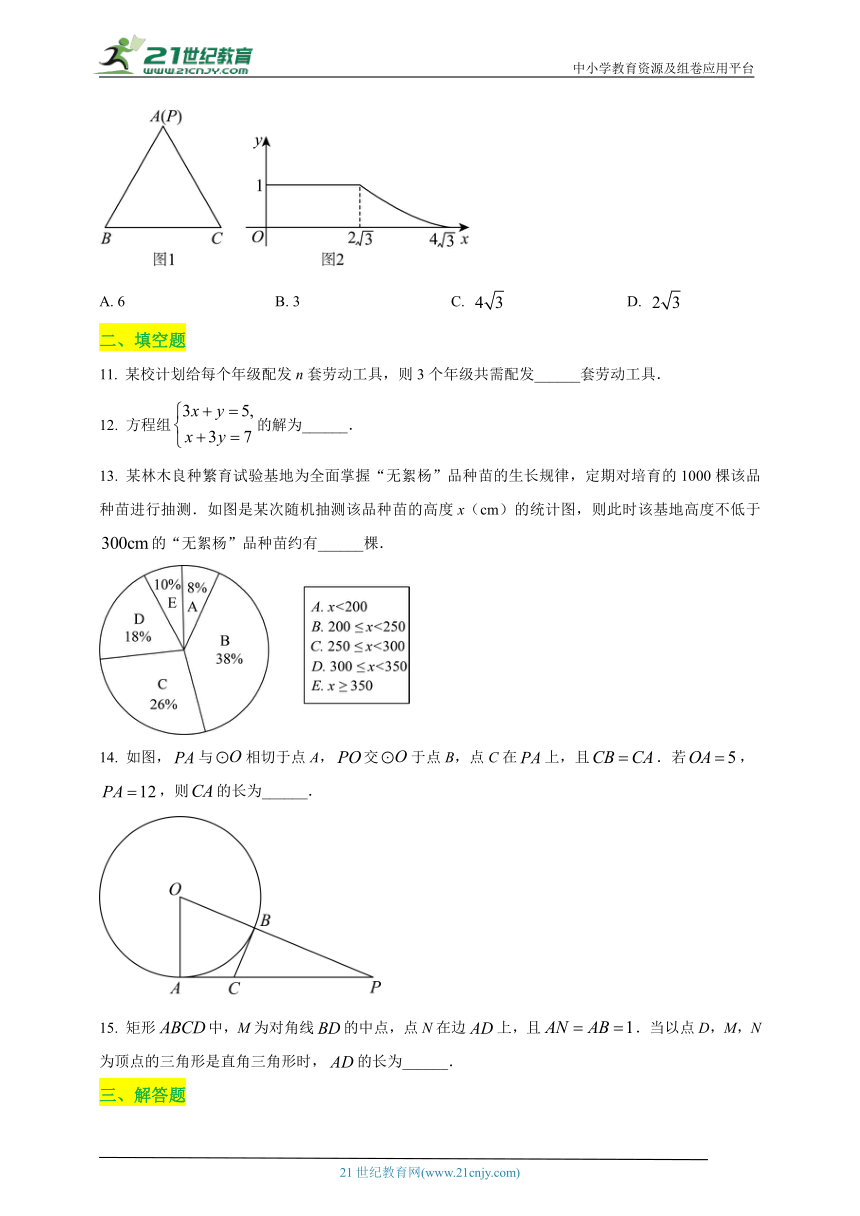
10. 如图1,点P从等边三角形的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为x,,图2是点P运动时y随x变化的关系图象,则等边三角形的边长为( )
A. 6 B. 3 C. D.
二、填空题
11. 某校计划给每个年级配发n套劳动工具,则3个年级共需配发______套劳动工具.
12. 方程组的解为______.
13. 某林木良种繁育试验基地为全面掌握“无絮杨”品种苗的生长规律,定期对培育的1000棵该品种苗进行抽测.如图是某次随机抽测该品种苗的高度x(cm)的统计图,则此时该基地高度不低于的“无絮杨”品种苗约有______棵.
14. 如图,与相切于点A,交于点B,点C在上,且.若,,则的长为______.
15. 矩形中,M为对角线的中点,点N在边上,且.当以点D,M,N为顶点的三角形是直角三角形时,的长为______.
三、解答题
16. (1)计算:;
(2)化简:.
17. 蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目 统计量 快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的______;______(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
18. 如图,中,点D在边上,且.
(1)请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).
(2)若(1)中所作的角平分线与边交于点E,连接.求证:.
19. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形和菱形,点D,E在x轴上,以点O为圆心,长为半径作,连接.
(1)求k的值;
(2)求扇形半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
20. 综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪为正方形,,顶点A处挂了一个铅锤M.如图是测量树高的示意图,测高仪上的点D,A与树顶E在一条直线上,铅垂线交于点H.经测量,点A距地面,到树的距离,.求树的高度(结果精确到).
21. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?请说明理由.
(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价.
(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为a元,请直接写出a的取值范围.
22. 小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网与y轴的水平距离,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
23. 李老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是李老师在“图形的变化”主题下设计的问题,请你解答.
(1)观察发现:如图1,在平面直角坐标系中,过点的直线轴,作关于轴对称的图形,再分别作关于轴和直线对称的图形和,则可以看作是绕点顺时针旋转得到的,旋转角的度数为______;可以看作是向右平移得到的,平移距离为______个单位长度.
(2)探究迁移:如图,中,,为直线下方一点,作点关于直线的对称点,再分别作点关于直线和直线的对称点和,连接,,请仅就图的情形解决以下问题:
①若,请判断与的数量关系,并说明理由;
②若,求,两点间的距离.
(3)拓展应用:在(2)条件下,若,,,连接.当与的边平行时,请直接写出的长.
参考答案及解析
一、选择题
1、【答案】A
【解析】解:因为,
所以最小的数是-1.
因此选:A
2、【答案】A
【解析】解:这个花鹅颈瓶的主视图与左视图相同,俯视图与主视图和左视图不同.
因此选:A.
3、【答案】C
【解析】解:4.59亿.
因此选:C.
4、【答案】B
【解析】解:因为,
所以,
又因为,
所以,
因此选:B
5、【答案】B
【解析】解:,
因此选:B.
6、【答案】D
【解析】解:因为,
所以由圆周角定理可得:,
因此选:D.
7、【答案】A
【解析】解:因为,
所以,
所以原方程有两个不相等的实数根.
因此选:A.
8、【答案】B
【解析】解:设三部影片依次为A、B、C,画树状图如下:
共有9种等可能的结果,其中七、八年级选择的影片相同的概率为.
因此选:B.
9、【答案】D
【解析】解:由图象开口向下,知,
由对称轴,得.
所以一次函数的图象经过第一、二、三象限,不经过第四象限.
因此选:D.
10、【答案】A
【解析】解:令点从顶点出发,沿直线运动到三角形内部一点,再从点沿直线运动到顶点.如图所示,
根据图象可知,当点在上运动时,,
∴,,
又∵为等边三角形,
∴,
∴,
∴,
∴,
当点在上运动时,点到达点时的路程为,
∴,即,
∴,
过点作,
∴,则,
∴,
即等边三角形的边长为6,
因此选:A.
二、填空题
11、【答案】
【解析】解:根据题意可知:3个年级共需配发的劳动工具总套数为:套,
因此答案为:.
12、【答案】
【解析】解:
由得,,解得:,
把代入①中得,解得:,
所以原方程组的解是,
因此答案为:.
13、【答案】280
【解析】解:根据题意,可知,该基地高度不低于的“无絮杨”品种苗所占百分比为,
则不低于“无絮杨”品种苗约为:棵,
因此答案:280.
14、【答案】
【解析】连接,如图所示,
∵与相切于点A,
∴;
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
设,则,
∴,
解得:,
所以的长为,
因此答案为:.
15、【答案】2或
【解析】解:当时,
∵四边形矩形,
∴,则,
由平行线分线段成比例可得:,
又∵M为对角线的中点,
∴,
∴,
即:,
∴,
当时,
∵M为对角线的中点,
∴为的垂直平分线,
∴,
∵四边形矩形,
∴,
则,
∴,
∴,
综上可知,的长为2或,
因此答案为:2或.
三、解答题
16、【答案】(1);
【解析】(1)解:原式;
(2)解:原式.
17、【答案】(1)7.5;
(2)甲公司,理由见解析
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
【解析】解:(1)根据题意可得,,
,
,
∴,
因此答案为:7.5;;
(2)∵根据配送速度得分可知,甲和乙的得分相差不大,
根据服务质量得分可知,甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲更稳定,
∴小丽应选择甲公司;
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
18、【答案】(1)见解析 (2)见解析
【解析】(1)解:如图所示即为所求,
(2)证明:∵平分,
∴,
∵,,
∴,
∴.
19、【答案】(1)
(2)半径为2,圆心角为
(3)
【解析】解:(1)将代入中,
得,
解得:;
(2)过点作的垂线,垂足为点,如图所示:
,
,
,
半径为2;
,
∴,
,
由菱形的性质可知:,
,
扇形的圆心角的度数:;
(3),
,
,
如图所示:由菱形知,,
,
,
.
20、【答案】树的高度为
【解析】解:根据题意得,,,
则,
∴,
∵,,
则,
∴,
又∵,则,
∴,
∴,
答:树的高度为.
21、【答案】(1)活动一更合算
(2)400元 (3)当或时,活动二更合算
【解析】解(1)购买一件原价为450元的健身器材时,
活动一需付款:元,活动二需付款:元,
所以活动一更合算;
(2)设这种健身器材的原价是元,
则,
解得:,
答:这种健身器材的原价是400元,
(3)这种健身器材的原价为a元,
则活动一需付款为:元,
活动二当时,需付款为:元,
当时,需付款为:元,
当时,需付款为:元,
①当时,,此时无论为何值,都是活动一更合算,不符合题意,
②当时,,解得,
即:当时,活动二更合算,
③当时,,解得,
即:当时,活动二更合算,
综上可知:当或时,活动二更合算.
22、【答案】(1),,
(2)选择吊球,使球的落地点到C点的距离更近
【解析】解:(1)在一次函数中,
令时,得,
∴,
将代入中,得:,
解得:;
(2)∵,,
∴,
选择扣球,则令,即,解得:,
即落地点距离点距离为,
所以落地点到C点的距离为,
选择吊球,则令,即,解得:(负值舍去),
即落地点距离点距离为,
所以落地点到C点的距离为,
∵,
∴选择吊球,使球的落地点到C点的距离更近.
23、【答案】(1),.
(2)①,理由见解析;②
(3)或
【解析】解:(1)∵关于轴对称的图形,与关于轴对称,
∴与关于点中心对称,
则可以看作是绕点顺时针旋转得到的,旋转角的度数为,
∵,
∴,
∵,关于直线对称,
∴,
即,
可以看作是向右平移得到的,平移距离为个单位长度.
因此答案为:,.
(2)①,理由如下,
连接, 如图所示,
由对称性可得,,
∴,
②连接分别交于两点,过点作,交于点,如图所示,
由对称性可知:且,
∵四边形为平行四边形,
∴,
∴三点共线,
∴,
∵,
∴,
∴四边形是矩形,
∴,
在中,,,
∵,
∴,
∴,
(3)设,则,
根据题意知,,
当时,过点作于点,如图所示,
∴,
∵,,
∴,,
∴,则,
在中,,
∴,则,
∴,
在中,,则,,
在中,,
,
∴,
由(2)②可得,
∵,
∴,
∴,
解得:;
若,则,如图所示,
∵,则,
则,
∵,,
∵,
∴,
解得:,
综上所述,的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年河南省数学中考真题名师详解版
一、选择题
1. 下列各数中,最小的数是( )
A -l B. 0 C. 1 D.
2. 北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A 主视图与左视图相同 B. 主视图与俯视图相同
C. 左视图与俯视图相同 D. 三种视图都相同
3. 2022年河南省出版4.59亿册图书,为贯彻落实党的二十大关于深化全民阅读活动的重要精神,建设学习型社会提供了丰富的图书资源.数据“4.59亿”用科学记数法表示为( )
A. B. C. D.
4. 如图,直线,相交于点O,若,,则的度数为( )
A. B. C. D.
5. 化简的结果是( )
A. 0 B. 1 C. a D.
6. 如图,点A,B,C在上,若,则的度数为( )
A. B. C. D.
7. 关于x的一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
8. 为落实教育部办公厅、中共中央宣传部办公厅关于《第41批向全国中小学生推荐优秀影片片目》的通知精神,某校七、八年级分别从如图所示的三部影片中随机选择一部组织本年级学生观看,则这两个年级选择的影片相同的概率为( )
A. B. C. D.
9. 二次函数的图象如图所示,则一次函数的图象一定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
10. 如图1,点P从等边三角形的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为x,,图2是点P运动时y随x变化的关系图象,则等边三角形的边长为( )
A. 6 B. 3 C. D.
二、填空题
11. 某校计划给每个年级配发n套劳动工具,则3个年级共需配发______套劳动工具.
12. 方程组的解为______.
13. 某林木良种繁育试验基地为全面掌握“无絮杨”品种苗的生长规律,定期对培育的1000棵该品种苗进行抽测.如图是某次随机抽测该品种苗的高度x(cm)的统计图,则此时该基地高度不低于的“无絮杨”品种苗约有______棵.
14. 如图,与相切于点A,交于点B,点C在上,且.若,,则的长为______.
15. 矩形中,M为对角线的中点,点N在边上,且.当以点D,M,N为顶点的三角形是直角三角形时,的长为______.
三、解答题
16. (1)计算:;
(2)化简:.
17. 蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目 统计量 快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的______;______(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
18. 如图,中,点D在边上,且.
(1)请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).
(2)若(1)中所作的角平分线与边交于点E,连接.求证:.
19. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形和菱形,点D,E在x轴上,以点O为圆心,长为半径作,连接.
(1)求k的值;
(2)求扇形半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
20. 综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪为正方形,,顶点A处挂了一个铅锤M.如图是测量树高的示意图,测高仪上的点D,A与树顶E在一条直线上,铅垂线交于点H.经测量,点A距地面,到树的距离,.求树的高度(结果精确到).
21. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?请说明理由.
(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价.
(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为a元,请直接写出a的取值范围.
22. 小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网与y轴的水平距离,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
23. 李老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是李老师在“图形的变化”主题下设计的问题,请你解答.
(1)观察发现:如图1,在平面直角坐标系中,过点的直线轴,作关于轴对称的图形,再分别作关于轴和直线对称的图形和,则可以看作是绕点顺时针旋转得到的,旋转角的度数为______;可以看作是向右平移得到的,平移距离为______个单位长度.
(2)探究迁移:如图,中,,为直线下方一点,作点关于直线的对称点,再分别作点关于直线和直线的对称点和,连接,,请仅就图的情形解决以下问题:
①若,请判断与的数量关系,并说明理由;
②若,求,两点间的距离.
(3)拓展应用:在(2)条件下,若,,,连接.当与的边平行时,请直接写出的长.
参考答案及解析
一、选择题
1、【答案】A
【解析】解:因为,
所以最小的数是-1.
因此选:A
2、【答案】A
【解析】解:这个花鹅颈瓶的主视图与左视图相同,俯视图与主视图和左视图不同.
因此选:A.
3、【答案】C
【解析】解:4.59亿.
因此选:C.
4、【答案】B
【解析】解:因为,
所以,
又因为,
所以,
因此选:B
5、【答案】B
【解析】解:,
因此选:B.
6、【答案】D
【解析】解:因为,
所以由圆周角定理可得:,
因此选:D.
7、【答案】A
【解析】解:因为,
所以,
所以原方程有两个不相等的实数根.
因此选:A.
8、【答案】B
【解析】解:设三部影片依次为A、B、C,画树状图如下:
共有9种等可能的结果,其中七、八年级选择的影片相同的概率为.
因此选:B.
9、【答案】D
【解析】解:由图象开口向下,知,
由对称轴,得.
所以一次函数的图象经过第一、二、三象限,不经过第四象限.
因此选:D.
10、【答案】A
【解析】解:令点从顶点出发,沿直线运动到三角形内部一点,再从点沿直线运动到顶点.如图所示,
根据图象可知,当点在上运动时,,
∴,,
又∵为等边三角形,
∴,
∴,
∴,
∴,
当点在上运动时,点到达点时的路程为,
∴,即,
∴,
过点作,
∴,则,
∴,
即等边三角形的边长为6,
因此选:A.
二、填空题
11、【答案】
【解析】解:根据题意可知:3个年级共需配发的劳动工具总套数为:套,
因此答案为:.
12、【答案】
【解析】解:
由得,,解得:,
把代入①中得,解得:,
所以原方程组的解是,
因此答案为:.
13、【答案】280
【解析】解:根据题意,可知,该基地高度不低于的“无絮杨”品种苗所占百分比为,
则不低于“无絮杨”品种苗约为:棵,
因此答案:280.
14、【答案】
【解析】连接,如图所示,
∵与相切于点A,
∴;
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
设,则,
∴,
解得:,
所以的长为,
因此答案为:.
15、【答案】2或
【解析】解:当时,
∵四边形矩形,
∴,则,
由平行线分线段成比例可得:,
又∵M为对角线的中点,
∴,
∴,
即:,
∴,
当时,
∵M为对角线的中点,
∴为的垂直平分线,
∴,
∵四边形矩形,
∴,
则,
∴,
∴,
综上可知,的长为2或,
因此答案为:2或.
三、解答题
16、【答案】(1);
【解析】(1)解:原式;
(2)解:原式.
17、【答案】(1)7.5;
(2)甲公司,理由见解析
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
【解析】解:(1)根据题意可得,,
,
,
∴,
因此答案为:7.5;;
(2)∵根据配送速度得分可知,甲和乙的得分相差不大,
根据服务质量得分可知,甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲更稳定,
∴小丽应选择甲公司;
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
18、【答案】(1)见解析 (2)见解析
【解析】(1)解:如图所示即为所求,
(2)证明:∵平分,
∴,
∵,,
∴,
∴.
19、【答案】(1)
(2)半径为2,圆心角为
(3)
【解析】解:(1)将代入中,
得,
解得:;
(2)过点作的垂线,垂足为点,如图所示:
,
,
,
半径为2;
,
∴,
,
由菱形的性质可知:,
,
扇形的圆心角的度数:;
(3),
,
,
如图所示:由菱形知,,
,
,
.
20、【答案】树的高度为
【解析】解:根据题意得,,,
则,
∴,
∵,,
则,
∴,
又∵,则,
∴,
∴,
答:树的高度为.
21、【答案】(1)活动一更合算
(2)400元 (3)当或时,活动二更合算
【解析】解(1)购买一件原价为450元的健身器材时,
活动一需付款:元,活动二需付款:元,
所以活动一更合算;
(2)设这种健身器材的原价是元,
则,
解得:,
答:这种健身器材的原价是400元,
(3)这种健身器材的原价为a元,
则活动一需付款为:元,
活动二当时,需付款为:元,
当时,需付款为:元,
当时,需付款为:元,
①当时,,此时无论为何值,都是活动一更合算,不符合题意,
②当时,,解得,
即:当时,活动二更合算,
③当时,,解得,
即:当时,活动二更合算,
综上可知:当或时,活动二更合算.
22、【答案】(1),,
(2)选择吊球,使球的落地点到C点的距离更近
【解析】解:(1)在一次函数中,
令时,得,
∴,
将代入中,得:,
解得:;
(2)∵,,
∴,
选择扣球,则令,即,解得:,
即落地点距离点距离为,
所以落地点到C点的距离为,
选择吊球,则令,即,解得:(负值舍去),
即落地点距离点距离为,
所以落地点到C点的距离为,
∵,
∴选择吊球,使球的落地点到C点的距离更近.
23、【答案】(1),.
(2)①,理由见解析;②
(3)或
【解析】解:(1)∵关于轴对称的图形,与关于轴对称,
∴与关于点中心对称,
则可以看作是绕点顺时针旋转得到的,旋转角的度数为,
∵,
∴,
∵,关于直线对称,
∴,
即,
可以看作是向右平移得到的,平移距离为个单位长度.
因此答案为:,.
(2)①,理由如下,
连接, 如图所示,
由对称性可得,,
∴,
②连接分别交于两点,过点作,交于点,如图所示,
由对称性可知:且,
∵四边形为平行四边形,
∴,
∴三点共线,
∴,
∵,
∴,
∴四边形是矩形,
∴,
在中,,,
∵,
∴,
∴,
(3)设,则,
根据题意知,,
当时,过点作于点,如图所示,
∴,
∵,,
∴,,
∴,则,
在中,,
∴,则,
∴,
在中,,则,,
在中,,
,
∴,
由(2)②可得,
∵,
∴,
∴,
解得:;
若,则,如图所示,
∵,则,
则,
∵,,
∵,
∴,
解得:,
综上所述,的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
