2023年湖北省荆州市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖北省荆州市数学中考真题名师详解版 试卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023年湖北省荆州市数学中考真题名师详解版
注意事项:
1.本卷满分为120分,考试时间为120分钟.
2.本卷是试题卷,不能答题,答题必须写在答题卡上。解答题中添加的辅助线、字母和符号等务必标在答题卡对应的图形上.
3.在答题卡上答题,选择题要用2B铅笔填涂,非选择题要用0.5毫米黑色中性笔作答.
一、选择题(本大题共有10个小题,每小题只有唯一正确答案,每小题3分,共30分)
1. 在实数,,,中,无理数是( )
A. B. C. D. 3.14
2. 下列各式运算正确是( )
A. B.
C. D.
3. 观察如图所示的几何体,下列关于其三视图的说法正确的是( )
A. 主视图既是中心对称图形,又是轴对称图形
B. 左视图既是中心对称图形,又是轴对称图形
C. 俯视图既是中心对称图形,又是轴对称图形
D. 主视图、左视图、俯视图都是中心对称图形
4. 已知蓄电池的电压为定值,使用蓄电池时,电流(单位:A)与电阻(单位:)是反比例函数关系.下列反映电流与电阻之间函数关系的图象大致是( )
A. B. C. D.
5. 已知,则与最接近的整数为( )
A. 2 B. 3 C. 4 D. 5
6. 为评估一种水稻的种植效果,选了10块地作试验田.这10块地的亩产量(单位:)分别为,下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是( )
A. 这组数据的平均数 B. 这组数据的方差
C. 这组数据的众数 D. 这组数据的中位数
7. 如图所示的“箭头”图形中,,,,则图中的度数是( )
A. B. C. D.
8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
9. 如图,直线分别与轴,轴交于点,,将绕着点顺时针旋转得到,则点的对应点的坐标是( )
A. B. C. D.
10. 如图,一条公路的转弯处是一段圆弧(),点是这段弧所在圆的圆心,为上一点,于.若,,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
11. 若,则___________.
12. 如图,为斜边上的中线,为的中点.若,,则___________.
13. 某校为了解学生对A,B,C,D四类运动的参与情况,随机调查了本校80名学生,让他们从中选择参与最多的一类,得到对应的人数分别是30,20,18,12.若该校有800名学生,则估计有___________人参与A类运动最多.
14. 如图,,点在上,,为内一点.根据图中尺规作图痕迹推断,点到的距离为___________.
15. 如图,无人机在空中处测得某校旗杆顶部仰角为,底部的俯角为,无人机与旗杆的水平距离为,则该校的旗杆高约为___________.(,结果精确到0.1)
16. 如图,点在双曲线上,将直线向上平移若干个单位长度交轴于点,交双曲线于点.若,则点的坐标是___________.
三、解答题(本大题共有8个小题,共72分)
17. 先化简,再求值:,其中,.
18. 已知关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围;
(2)当时,用配方法解方程.
19. 如图,是等边的中线,以为圆心,的长为半径画弧,交的延长线于,连接.求证:.
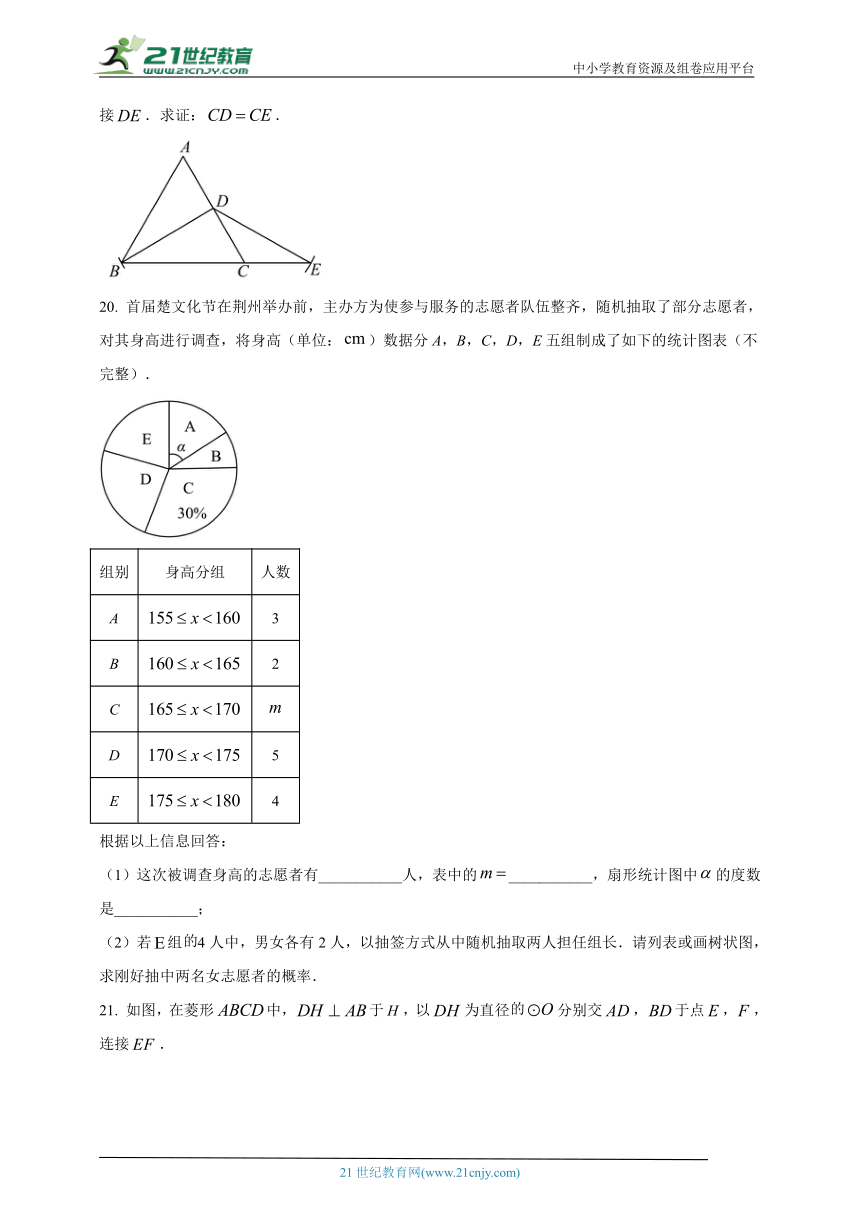
20. 首届楚文化节在荆州举办前,主办方为使参与服务的志愿者队伍整齐,随机抽取了部分志愿者,对其身高进行调查,将身高(单位:)数据分A,B,C,D,E五组制成了如下的统计图表(不完整).
组别 身高分组 人数
A 3
B 2
C
D 5
E 4
根据以上信息回答:
(1)这次被调查身高的志愿者有___________人,表中的___________,扇形统计图中的度数是___________;
(2)若组4人中,男女各有2人,以抽签方式从中随机抽取两人担任组长.请列表或画树状图,求刚好抽中两名女志愿者的概率.
21. 如图,在菱形中,于,以为直径分别交,于点,,连接.
(1)求证:
①是的切线;
②;
(2)若,,求.
22. 荆州古城旁“荆街”某商铺打算购进,两种文创饰品对游客销售.已知1400元采购种的件数是630元采购种件数的2倍,种的进价比种的进价每件多1元,两种饰品的售价均为每件15元;计划采购这两种饰品共600件,采购种的件数不低于390件,不超过种件数的4倍.
(1)求,饰品每件的进价分别为多少元?
(2)若采购这两种饰品只有一种情况可优惠,即一次性采购种超过150件时,种超过的部分按进价打6折.设购进种饰品件,
①求的取值范围;
②设计能让这次采购的饰品获利最大的方案,并求出最大利润.
23. 如图1,点是线段上与点,点不重合的任意一点,在的同侧分别以,,为顶点作,其中与的一边分别是射线和射线,的两边不在直线上,我们规定这三个角互为等联角,点为等联点,线段为等联线.
(1)如图2,在个方格纸上,小正方形的顶点为格点、边长均为1,为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段为等联线、某格点为等联点的等联角,并标出等联角,保留作图痕迹;
(2)如图3,在中,,,延长至点,使,作的等联角和.将沿折叠,使点落在点处,得到,再延长交的延长线于,连接并延长交的延长线于,连接.
①确定的形状,并说明理由;
②若,,求等联线和线段的长(用含的式子表示).
24. 已知:关于的函数.
(1)若函数的图象与坐标轴有两个公共点,且,则的值是___________;
(2)如图,若函数的图象为抛物线,与轴有两个公共点,,并与动直线交于点,连接,,,,其中交轴于点,交于点.设的面积为,的面积为.
①当点为抛物线顶点时,求的面积;
②探究直线在运动过程中,是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:在实数,,,中,无理数是,
因此选:B.
2、【答案】A
【解析】解:A. ,所以该选项正确,符合题意;
B. ,所以该选项不正确,不符合题意;
C. ,所以该选项不正确,不符合题意;
D. ,所以该选项不正确,不符合题意;
因此选:A.
3、【答案】C
【解析】解:A选项:主视图是上下两个等腰三角形,不是中心对称图形,是轴对称图形,所以不符合题意;
B选项:左视图是上下两个等腰三角形,不是中心对称图形,是轴对称图形,所以不符合题意;
C选项:俯视图是圆(带圆心),既是中心对称图形,又是轴对称图形,所以符合题意;
D选项:由A和B选项可知,主视图和左视图都不是中心对称图形,所以不符合题意.
因此选:C.
4、【答案】D
【解析】因为反比例函数的图象是双曲线,且,,
所以图象是第一象限双曲线的一支.
因此选:D.
5、【答案】B
【解析】解:
∵,
∴,
∴与最接近的整数为,
因此选:B.
6、【答案】B
【解析】解:根据题意,给出统计量中可以用来评估这种水稻亩产量稳定程度的是这组数据的方差,
因此选:B.
7、【答案】C
【解析】解:如图所示,延长交于点,延长交于点,过点作的平行线,
,
,,
,
,
,,
,
因此选:C.
8、【答案】A
【解析】解:设木条长x尺,绳子长y尺,
所以可列方程组为:,
因此选:A.
9、【答案】C
【解析】解:∵直线分别与轴,轴交于点,,
∴当时,,即,则,
当时,,即,则,
∵将绕着点顺时针旋转得到,
又∵
∴,,,
∴,
延长交轴于点,则,,
∴,
因此选:C.
10、【答案】B
【解析】解: ,点是这段弧所在圆的圆心,
,,
,,
,
.
,,
.
设,则,
在中,,
,
.
,
,
.
因此选:B.
二、填空题
11、【答案】
【解析】解:∵,
∴,
解得:,
∴,
因此答案为:.
12、【答案】3
【解析】解:∵在中,为斜边上的中线,,
∴,
∴,
∵为的中点,
∴
因此答案为:3.
13、【答案】300
【解析】解:(人).
估计有300人参与A类运动最多.
因此答案为:300.
14、【答案】1
【解析】如图所示,
由尺规作图痕迹可得,是的垂直平分线,
∴,
∴,
设,则,
∵,
∴,
∴,
∴,
由尺规作图痕迹可得,是的平分线,
∴点到的距离等于点P到的距离,即的长度,
∴点到的距离为1.
因此答案为:1 .
15、【答案】13.8####
【解析】解:依题意可得,
在中,,
,
在中,,
,
,
因此答案为:.
16、【答案】
【解析】解:把代入,可得,解得,
所以反比例函数解析式,
如图所示,过点作轴的垂线段交轴于点,过点作轴的垂线段交轴于点,
,
,
,
,
将直线向上平移若干个单位长度交轴于点,
,
中,,
,
即点C的横坐标为,
把代入,可得,
,
因此答案为:.
三、解答题
17、【答案】,2
【解析】解:
,
原式.
18、【答案】(1)且
(2),
【解析】解:(1)依题意得:,
解得:且;
(2)当时,原方程变为:,
则有:,
,
,
方程的根为,.
19、【答案】见解析
【解析】证明:为等边的中线,
,
,
,
20、【答案】(1)20,6,
(2)
【解析】解:(1)∵
∴
∴
故填:20, 6,;
(2)画树状图为:
或者列表为:
男1 男2 女1 女2
男1 (男1男2) (男1女1) (男1女2)
男2 (男2男1) (男2女1) (男2女2)
女1 (女1男1) (女1男2) (女1女2)
女2 (女2男1) (女2男2) (女2女1)
共有12种等可能结果,其中抽中两名女志愿者的结果有2种
(抽中两名女志愿者).
21、【答案】(1)①见解析,②见解析
(2)
【解析】(1)证明:①四边形是菱形,
,
,则
又为的半径的外端点,
是的切线.
②如图,连接,
∵
∴
为直径,
,
而
,
又
.
(2)解:如图,连接交于.
菱形,,
,,,
在中,,
,
,
,
在中,,
由得:,
.
22、【答案】(1)种饰品每件进价为10元,B种饰品每件进价为9元;
(2)①且为整数,②当采购种饰品210件,B种饰品390件时,商铺获利最大,最大利润为3630元.
【解析】解:(1)设种饰品每件的进价为元,则B种饰品每件的进价为元.
由题意得:,解得:,
经检验,是所列方程的根,且符合题意.
种饰品每件进价为10元,B种饰品每件进价为9元.
(2)①依题意得:,
解得:且为整数;
②设采购种饰品件时的总利润为元.
当时,,
即,
,
随的增大而减小.
当时,有最大值3480.
当时,
整理得:,
,
随的增大而增大.
当时,有最大值3630.
,
的最大值为3630,此时.
即当采购种饰品210件,B种饰品390件时,商铺获利最大,最大利润为3630元.
23、【答案】(1)见解析 (2)①等腰直角三角形,见解析;②;
【解析】
解:(1)如图所示(方法不唯一)
(2)①是等腰直角三角形.理由为:
如图,过点作交的延长线于.
由折叠得,,
,,
四边形为正方形
又,
,而,
是等腰直角三角形.
②过点作于,交的延长线于,则.
,
,
由是等腰直角三角形知:,
,
,,而,
,
在中,,,
,
,
,
由,,
∴四边形为正方形,,
由,得:,
∴,
,而,
即,解得:,
由①知:,,
.
24、【答案】(1)0或2或
(2)①6,②存在,
【解析】解:(1)函数的图象与坐标轴有两个公共点,
,
,
,
当函数为一次函数时,,
.
当函数为二次函数时,
,
若函数的图象与坐标轴有两个公共点,即与轴,轴分别只有一个交点时,
,
.
当函数为二次函数时,函数的图象与坐标轴有两个公共点, 即其中一点经过原点,
,
,
.
综上所述,或0.
故答案为:0或2或.
(2)①如图所示,设直线与交于点,直线与交于点.
依题意得:,解得:
抛物线的解析式为:.
点为抛物线顶点时,,,
,,
由,得直线的解析式为,
在直线上,且在直线上,则的横坐标等于的横坐标,
,
,,
,
.
②存在最大值,理由如下:
如图,设直线交轴于.
由①得:,,,,,
,
,,
,
,
即,
,,
,
,
,,
当时,有最大值,最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖北省荆州市数学中考真题名师详解版
注意事项:
1.本卷满分为120分,考试时间为120分钟.
2.本卷是试题卷,不能答题,答题必须写在答题卡上。解答题中添加的辅助线、字母和符号等务必标在答题卡对应的图形上.
3.在答题卡上答题,选择题要用2B铅笔填涂,非选择题要用0.5毫米黑色中性笔作答.
一、选择题(本大题共有10个小题,每小题只有唯一正确答案,每小题3分,共30分)
1. 在实数,,,中,无理数是( )
A. B. C. D. 3.14
2. 下列各式运算正确是( )
A. B.
C. D.
3. 观察如图所示的几何体,下列关于其三视图的说法正确的是( )
A. 主视图既是中心对称图形,又是轴对称图形
B. 左视图既是中心对称图形,又是轴对称图形
C. 俯视图既是中心对称图形,又是轴对称图形
D. 主视图、左视图、俯视图都是中心对称图形
4. 已知蓄电池的电压为定值,使用蓄电池时,电流(单位:A)与电阻(单位:)是反比例函数关系.下列反映电流与电阻之间函数关系的图象大致是( )
A. B. C. D.
5. 已知,则与最接近的整数为( )
A. 2 B. 3 C. 4 D. 5
6. 为评估一种水稻的种植效果,选了10块地作试验田.这10块地的亩产量(单位:)分别为,下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是( )
A. 这组数据的平均数 B. 这组数据的方差
C. 这组数据的众数 D. 这组数据的中位数
7. 如图所示的“箭头”图形中,,,,则图中的度数是( )
A. B. C. D.
8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
9. 如图,直线分别与轴,轴交于点,,将绕着点顺时针旋转得到,则点的对应点的坐标是( )
A. B. C. D.
10. 如图,一条公路的转弯处是一段圆弧(),点是这段弧所在圆的圆心,为上一点,于.若,,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
11. 若,则___________.
12. 如图,为斜边上的中线,为的中点.若,,则___________.
13. 某校为了解学生对A,B,C,D四类运动的参与情况,随机调查了本校80名学生,让他们从中选择参与最多的一类,得到对应的人数分别是30,20,18,12.若该校有800名学生,则估计有___________人参与A类运动最多.
14. 如图,,点在上,,为内一点.根据图中尺规作图痕迹推断,点到的距离为___________.
15. 如图,无人机在空中处测得某校旗杆顶部仰角为,底部的俯角为,无人机与旗杆的水平距离为,则该校的旗杆高约为___________.(,结果精确到0.1)
16. 如图,点在双曲线上,将直线向上平移若干个单位长度交轴于点,交双曲线于点.若,则点的坐标是___________.
三、解答题(本大题共有8个小题,共72分)
17. 先化简,再求值:,其中,.
18. 已知关于的一元二次方程有两个不相等的实数根.
(1)求的取值范围;
(2)当时,用配方法解方程.
19. 如图,是等边的中线,以为圆心,的长为半径画弧,交的延长线于,连接.求证:.
20. 首届楚文化节在荆州举办前,主办方为使参与服务的志愿者队伍整齐,随机抽取了部分志愿者,对其身高进行调查,将身高(单位:)数据分A,B,C,D,E五组制成了如下的统计图表(不完整).
组别 身高分组 人数
A 3
B 2
C
D 5
E 4
根据以上信息回答:
(1)这次被调查身高的志愿者有___________人,表中的___________,扇形统计图中的度数是___________;
(2)若组4人中,男女各有2人,以抽签方式从中随机抽取两人担任组长.请列表或画树状图,求刚好抽中两名女志愿者的概率.
21. 如图,在菱形中,于,以为直径分别交,于点,,连接.
(1)求证:
①是的切线;
②;
(2)若,,求.
22. 荆州古城旁“荆街”某商铺打算购进,两种文创饰品对游客销售.已知1400元采购种的件数是630元采购种件数的2倍,种的进价比种的进价每件多1元,两种饰品的售价均为每件15元;计划采购这两种饰品共600件,采购种的件数不低于390件,不超过种件数的4倍.
(1)求,饰品每件的进价分别为多少元?
(2)若采购这两种饰品只有一种情况可优惠,即一次性采购种超过150件时,种超过的部分按进价打6折.设购进种饰品件,
①求的取值范围;
②设计能让这次采购的饰品获利最大的方案,并求出最大利润.
23. 如图1,点是线段上与点,点不重合的任意一点,在的同侧分别以,,为顶点作,其中与的一边分别是射线和射线,的两边不在直线上,我们规定这三个角互为等联角,点为等联点,线段为等联线.
(1)如图2,在个方格纸上,小正方形的顶点为格点、边长均为1,为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段为等联线、某格点为等联点的等联角,并标出等联角,保留作图痕迹;
(2)如图3,在中,,,延长至点,使,作的等联角和.将沿折叠,使点落在点处,得到,再延长交的延长线于,连接并延长交的延长线于,连接.
①确定的形状,并说明理由;
②若,,求等联线和线段的长(用含的式子表示).
24. 已知:关于的函数.
(1)若函数的图象与坐标轴有两个公共点,且,则的值是___________;
(2)如图,若函数的图象为抛物线,与轴有两个公共点,,并与动直线交于点,连接,,,,其中交轴于点,交于点.设的面积为,的面积为.
①当点为抛物线顶点时,求的面积;
②探究直线在运动过程中,是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
参考答案及解析
一、选择题
1、【答案】B
【解析】解:在实数,,,中,无理数是,
因此选:B.
2、【答案】A
【解析】解:A. ,所以该选项正确,符合题意;
B. ,所以该选项不正确,不符合题意;
C. ,所以该选项不正确,不符合题意;
D. ,所以该选项不正确,不符合题意;
因此选:A.
3、【答案】C
【解析】解:A选项:主视图是上下两个等腰三角形,不是中心对称图形,是轴对称图形,所以不符合题意;
B选项:左视图是上下两个等腰三角形,不是中心对称图形,是轴对称图形,所以不符合题意;
C选项:俯视图是圆(带圆心),既是中心对称图形,又是轴对称图形,所以符合题意;
D选项:由A和B选项可知,主视图和左视图都不是中心对称图形,所以不符合题意.
因此选:C.
4、【答案】D
【解析】因为反比例函数的图象是双曲线,且,,
所以图象是第一象限双曲线的一支.
因此选:D.
5、【答案】B
【解析】解:
∵,
∴,
∴与最接近的整数为,
因此选:B.
6、【答案】B
【解析】解:根据题意,给出统计量中可以用来评估这种水稻亩产量稳定程度的是这组数据的方差,
因此选:B.
7、【答案】C
【解析】解:如图所示,延长交于点,延长交于点,过点作的平行线,
,
,,
,
,
,,
,
因此选:C.
8、【答案】A
【解析】解:设木条长x尺,绳子长y尺,
所以可列方程组为:,
因此选:A.
9、【答案】C
【解析】解:∵直线分别与轴,轴交于点,,
∴当时,,即,则,
当时,,即,则,
∵将绕着点顺时针旋转得到,
又∵
∴,,,
∴,
延长交轴于点,则,,
∴,
因此选:C.
10、【答案】B
【解析】解: ,点是这段弧所在圆的圆心,
,,
,,
,
.
,,
.
设,则,
在中,,
,
.
,
,
.
因此选:B.
二、填空题
11、【答案】
【解析】解:∵,
∴,
解得:,
∴,
因此答案为:.
12、【答案】3
【解析】解:∵在中,为斜边上的中线,,
∴,
∴,
∵为的中点,
∴
因此答案为:3.
13、【答案】300
【解析】解:(人).
估计有300人参与A类运动最多.
因此答案为:300.
14、【答案】1
【解析】如图所示,
由尺规作图痕迹可得,是的垂直平分线,
∴,
∴,
设,则,
∵,
∴,
∴,
∴,
由尺规作图痕迹可得,是的平分线,
∴点到的距离等于点P到的距离,即的长度,
∴点到的距离为1.
因此答案为:1 .
15、【答案】13.8####
【解析】解:依题意可得,
在中,,
,
在中,,
,
,
因此答案为:.
16、【答案】
【解析】解:把代入,可得,解得,
所以反比例函数解析式,
如图所示,过点作轴的垂线段交轴于点,过点作轴的垂线段交轴于点,
,
,
,
,
将直线向上平移若干个单位长度交轴于点,
,
中,,
,
即点C的横坐标为,
把代入,可得,
,
因此答案为:.
三、解答题
17、【答案】,2
【解析】解:
,
原式.
18、【答案】(1)且
(2),
【解析】解:(1)依题意得:,
解得:且;
(2)当时,原方程变为:,
则有:,
,
,
方程的根为,.
19、【答案】见解析
【解析】证明:为等边的中线,
,
,
,
20、【答案】(1)20,6,
(2)
【解析】解:(1)∵
∴
∴
故填:20, 6,;
(2)画树状图为:
或者列表为:
男1 男2 女1 女2
男1 (男1男2) (男1女1) (男1女2)
男2 (男2男1) (男2女1) (男2女2)
女1 (女1男1) (女1男2) (女1女2)
女2 (女2男1) (女2男2) (女2女1)
共有12种等可能结果,其中抽中两名女志愿者的结果有2种
(抽中两名女志愿者).
21、【答案】(1)①见解析,②见解析
(2)
【解析】(1)证明:①四边形是菱形,
,
,则
又为的半径的外端点,
是的切线.
②如图,连接,
∵
∴
为直径,
,
而
,
又
.
(2)解:如图,连接交于.
菱形,,
,,,
在中,,
,
,
,
在中,,
由得:,
.
22、【答案】(1)种饰品每件进价为10元,B种饰品每件进价为9元;
(2)①且为整数,②当采购种饰品210件,B种饰品390件时,商铺获利最大,最大利润为3630元.
【解析】解:(1)设种饰品每件的进价为元,则B种饰品每件的进价为元.
由题意得:,解得:,
经检验,是所列方程的根,且符合题意.
种饰品每件进价为10元,B种饰品每件进价为9元.
(2)①依题意得:,
解得:且为整数;
②设采购种饰品件时的总利润为元.
当时,,
即,
,
随的增大而减小.
当时,有最大值3480.
当时,
整理得:,
,
随的增大而增大.
当时,有最大值3630.
,
的最大值为3630,此时.
即当采购种饰品210件,B种饰品390件时,商铺获利最大,最大利润为3630元.
23、【答案】(1)见解析 (2)①等腰直角三角形,见解析;②;
【解析】
解:(1)如图所示(方法不唯一)
(2)①是等腰直角三角形.理由为:
如图,过点作交的延长线于.
由折叠得,,
,,
四边形为正方形
又,
,而,
是等腰直角三角形.
②过点作于,交的延长线于,则.
,
,
由是等腰直角三角形知:,
,
,,而,
,
在中,,,
,
,
,
由,,
∴四边形为正方形,,
由,得:,
∴,
,而,
即,解得:,
由①知:,,
.
24、【答案】(1)0或2或
(2)①6,②存在,
【解析】解:(1)函数的图象与坐标轴有两个公共点,
,
,
,
当函数为一次函数时,,
.
当函数为二次函数时,
,
若函数的图象与坐标轴有两个公共点,即与轴,轴分别只有一个交点时,
,
.
当函数为二次函数时,函数的图象与坐标轴有两个公共点, 即其中一点经过原点,
,
,
.
综上所述,或0.
故答案为:0或2或.
(2)①如图所示,设直线与交于点,直线与交于点.
依题意得:,解得:
抛物线的解析式为:.
点为抛物线顶点时,,,
,,
由,得直线的解析式为,
在直线上,且在直线上,则的横坐标等于的横坐标,
,
,,
,
.
②存在最大值,理由如下:
如图,设直线交轴于.
由①得:,,,,,
,
,,
,
,
即,
,,
,
,
,,
当时,有最大值,最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
