2023年湖北省潜江 天门 仙桃 江汉 油田数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖北省潜江 天门 仙桃 江汉 油田数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年湖北省潜江 天门 仙桃 江汉 油田数学中考真题名师详解版
(本卷共6页,满分120分,考试时间120分钟)
注意事项:
1.答题前,考生务必将自己的姓名,准考证号填写在试卷第1页装订线内和答题卡上,并在答题卡的规定位置贴好条形码,核准姓名和准考证号.
2.选择题的答案选出后,必须使用2B铅笔把答题卡上对应的答案标号涂黑.如需改动,先用橡皮擦干净后,再选涂其他答案标号.非选择题答案必须使用0,5mm黑色墨水签字笔填写在答题卡对应的区域内,写在本试卷上无效.
3.考试结束后,请将本试卷和答题卡一并交回.
一、选择题(本大题共10个小题,每小题3分,满分30分.在下列每个小题给出的四个答案中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分)
1. 的绝对值是( )
A. B. C. D.
2. 2023年全国高考报名人数约12910000人,数12910000用科学记数法表示( )
A. B. C. D.
3. 如图是一个立体图形的三视图,该立体图形是( )
A. 三棱柱 B. 圆柱 C. 三棱锥 D. 圆锥
4. 不等式组的解集是( )
A B. C. D.
5. 某班9名学生参加定点投篮测试,每人投篮10次,投中的次数统计如下:3,6,4,6,4,3,6,5,7.这组数据的中位数和众数分别是( )
A 5,4 B. 5,6 C. 6,5 D. 6,6
6. 在反比例函数的图象上有两点,当时,有,则的取值范围是( )
A. B. C. D.
7. 如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点外接圆的一部分,小正方形边长为1,图中阴影部分的面积为( )
A. B. C. D.
8. 如图,在中,,点在边上,且平分的周长,则的长是( )
A. B. C. D.
9. 拋物线与轴相交于点.下列结论:
①;②;③;④若点在抛物线上,且,则.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
10. 如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为(细实线)表示铁桶中水面高度,(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则随时间变化的函数图象大致为( )
A. B. C. D.
二、填空题(本大题共5个小题,每小题3分,满分15分,请将答案直接填在答线卡对应的横线上)
11. 计算的结果是_________.
12. 在平面直角坐标系中,若反比例函数的图象经过点和点,则的面积为_________.
13. 如图,在中,内切圆与分别相切于点,,连接的延长线交于点,则_________.
14. 有四张背面完全相同的卡片,正面分别画了等腰三角形,平行四边形,正五边形,圆,现将卡片背面朝上并洗匀,从中随机抽取一张,记下卡片上的图形后(不放回),再从中随机抽取一张,则抽取的两张卡片上的图形都是中心对称图形的概率为_________.
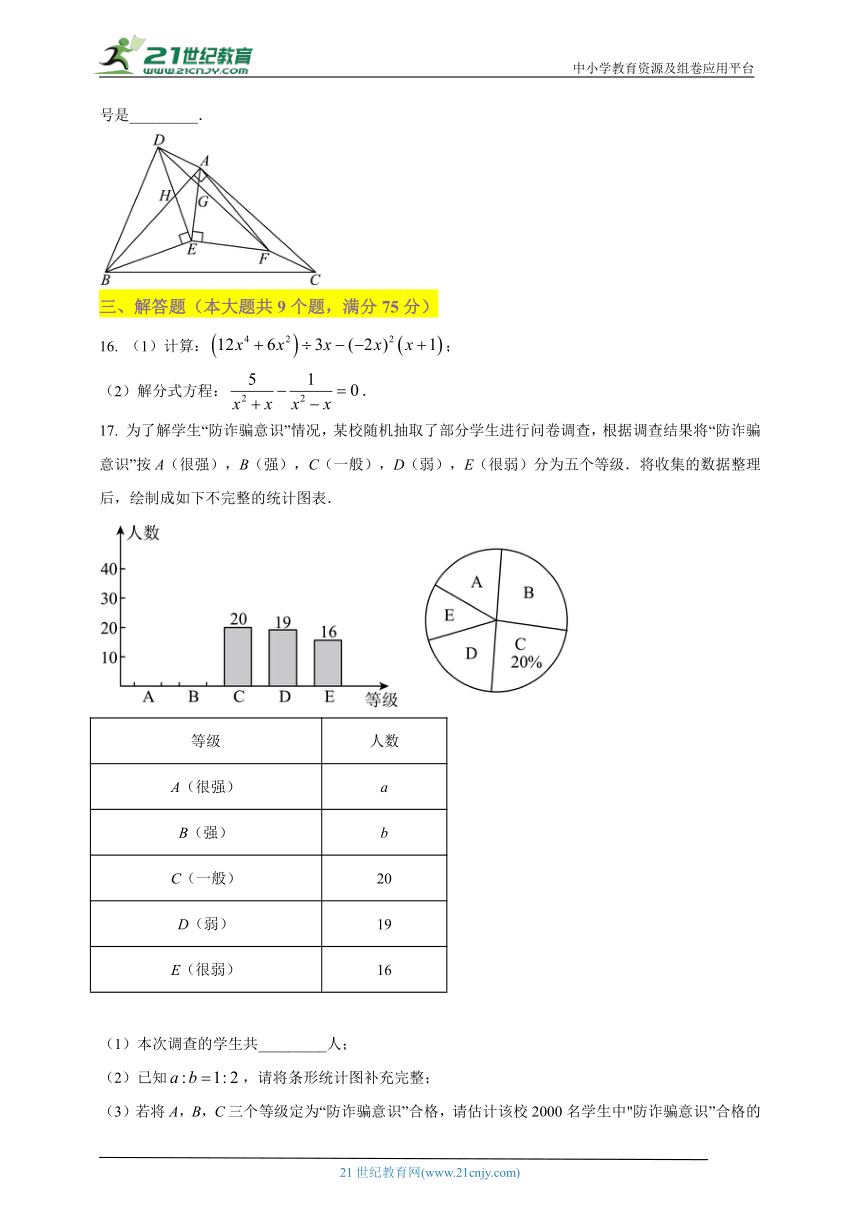
15. 如图,和都是等腰直角三角形,,点在内,,连接交于点交于点,连接.给出下面四个结论:①;②;③;④.其中所有正确结论的序号是_________.
三、解答题(本大题共9个题,满分75分)
16. (1)计算:;
(2)解分式方程:.
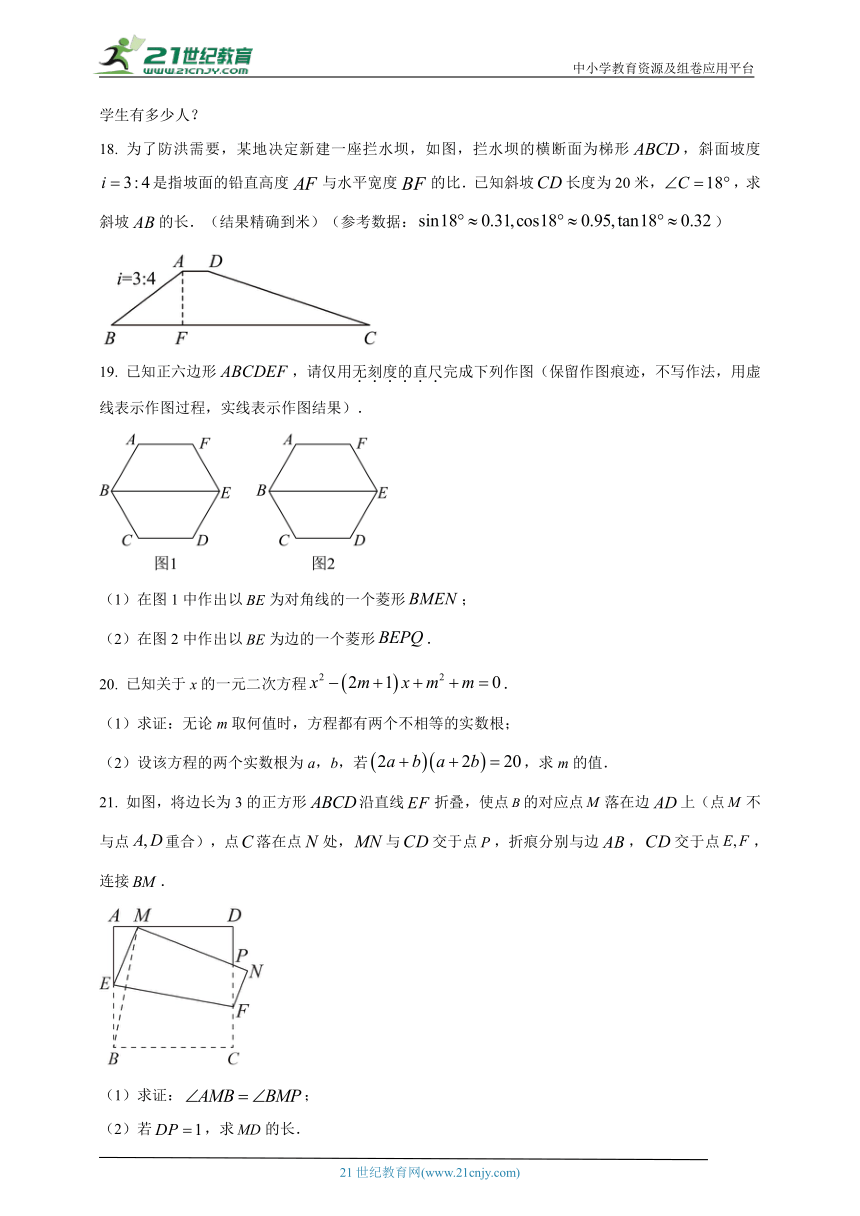
17. 为了解学生“防诈骗意识”情况,某校随机抽取了部分学生进行问卷调查,根据调查结果将“防诈骗意识”按A(很强),B(强),C(一般),D(弱),E(很弱)分为五个等级.将收集的数据整理后,绘制成如下不完整的统计图表.
等级 人数
A(很强) a
B(强) b
C(一般) 20
D(弱) 19
E(很弱) 16
(1)本次调查的学生共_________人;
(2)已知,请将条形统计图补充完整;
(3)若将A,B,C三个等级定为“防诈骗意识”合格,请估计该校2000名学生中"防诈骗意识”合格的学生有多少人?
18. 为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米,,求斜坡的长.(结果精确到米)(参考数据:)
19. 已知正六边形,请仅用无刻度的直尺完成下列作图(保留作图痕迹,不写作法,用虚线表示作图过程,实线表示作图结果).
(1)在图1中作出以为对角线的一个菱形;
(2)在图2中作出以为边的一个菱形.
20. 已知关于x的一元二次方程.
(1)求证:无论m取何值时,方程都有两个不相等的实数根;
(2)设该方程的两个实数根为a,b,若,求m的值.
21. 如图,将边长为3的正方形沿直线折叠,使点的对应点落在边上(点不与点重合),点落在点处,与交于点,折痕分别与边,交于点,连接.
(1)求证:;
(2)若,求的长.
22. 某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:
时间:第x(天)
日销售价(元/件) 50
日销售量(件)
(,x为整数)
设该商品的日销售利润为w元.
(1)直接写出w与x的函数关系式__________________;
(2)该商品在第几天的日销售利润最大?最大日销售利润是多少?
23. 如图,等腰内接于,,是边上的中线,过点作的平行线交的延长线于点,交于点,连接.
(1)求证:为切线;
(2)若的半径为,,求的长.
24. 如图1,在平面直角坐标系中,已知抛物线与轴交于点,与轴交于点,顶点为,连接.
(1)抛物线的解析式为__________________;(直接写出结果)
(2)在图1中,连接并延长交的延长线于点,求的度数;
(3)如图2,若动直线与抛物线交于两点(直线与不重合),连接,直线与交于点.当时,点的横坐标是否为定值,请说明理由.
参考答案及解析
一、选择题
1、【答案】D
【解析】解:.
因此选:D.
2、【答案】B
【解析】解:数12910000用科学记数法表示为.
因此选:B.
3、【答案】D
【解析】解:由主视图和左视图为三角形判断出是锥体,
根据俯视图是圆可判断出这个几何体应该是圆锥.
因此选:D.
4、【答案】A
【解析】解:
解不等式①得:,
解不等式②得:,
所以不等式组的解集为,
因此选A.
5、【答案】B
【解析】解:这组数据3,6,4,6,4,3,6,5,7中出现次数最多的是6,
众数是6.
将这组数据3,6,4,6,4,3,6,5,7按从小到大顺序排列是3,3,4,4,5,6, 6, 6, 7,
中位数为:5.
因此选:B
6、【答案】C
【解析】解:因为当时,有,
所以反比例函数的图象在一三象限,
所以
解得:,
因此选:C.
7、【答案】D
【解析】解:如图所示,作的垂直平分线,作的垂直平分线,设与相交于点O,连接,则点O是外接圆的圆心,
由题意得:,,,
∴,
∴是直角三角形,
∴,
∵,
∴
,
因此选:D.
8、【答案】C
【解析】解:如图所示,过点B作于点E,
∵在中,,
∴,
∵,
∴,
∴,
∵平分的周长,
∴,即,
又∵,
∴,
∴,
∴,
因此选C.
9、【答案】B
【解析】解:①由题意得:,
∴,
∵,
∴,
∴,所以①错误;
②∵抛物线与x轴相交于点.
∴有两个不相等的实数根,
∴,所以②正确;
③∵,
∴,所以③正确;
④∵抛物线与x轴相交于点.
∴抛物线的对称轴为:,
当点在抛物线上,且,
∴或,
解得:,所以④错误,
综上,②③正确,共2个,
因此选:B.
10、【答案】C
【解析】解:由图象知,时,铁桶注满了水,,是一条斜线段,,是一条水平线段,
当时,长方体水池开始注入水;当时,长方体水池中的水没过铁桶,水池中水面高度比之开始变得平缓;当时,长方体水池满了水,
所以开始是一段陡线段,后变缓,最后是一条水平线段,
观察函数图象,选项C符合题意,
因此选:C.
填空题
11、【答案】1
【解析】解:
,
因此答案为:1.
12、【答案】
【解析】解:反比例函数的图象经过点,
,
.
反比例函数为:.
反比例函数的图象经过点,
,
.
如图所示,过点作于点,过点作的延长线于点,设与轴的交点为,
,,
,,,
.
因此答案为:.
13、【答案】##度
【解析】解:如图所示,连接,设交于点H,
∵是的内切圆,
∴分别是的角平分线,
∴,
∵,
∴,
∴,
∴,
∵与分别相切于点,,
∴,
又∵,
∴是的垂直平分线,
∴,即,
∴,
因此答案为:.
14、【答案】
【解析】解:分别用,,,表示等腰三角形,平行四边形,正五边形,圆,画树状图如下:
依题意且由图知,共有12种等可能的结果,其中两次抽出的图形都是中心对称图形的有2种,
所以两次抽出的图形都是中心对称图形的概率为:.
因此答案为.
15、【答案】①③④
【解析】解:∵和都是等腰直角三角形,
∴,,,,
∵,,
∴,所以①正确;
∴,
∴,,所以③正确;
∵,,,
∴,;故②错误;
∴,
∵,
∴四边形是平行四边形,
∴,所以④正确;
因此答案为①③④.
解答题
16、【答案】(1);(2)
【解析】(1)解:原式
;
(2)解:两边乘以,得.
解得:.
经检验,是原分式方程的解.
17、【答案】(1)共100人
(2)见解析 (3)估计该校2000名学生中“防诈骗意识”合格的学生有1300人
【解析】解:(1)由统计图可知:(人);
故答案为100;
(2)由(1)得:,
∵,
∴,
补全条形统计图如下:
(3)由题意得:
(人).
所以估计该校2000名学生中“防诈骗意识”合格的学生有1300人.
18、【答案】斜坡的长约为10米
【解析】解:过点作于点,则四边形是矩形,
在中,,
.
∴.
∵,
∴在中,(米).
答:斜坡的长约为10米.
19、【答案】(1)见解析 (2)见解析
【解析】解:(1)如图所示,菱形即为所求(点,可以对调位置):
(2)如图,菱形即为所求.
是菱形,且要求为边,
①当为上底边的时候,作,且,向右下偏移,如图所示,
②当为上底边的时候,作,且,向左下偏移如图所示,
③当为下底边的时候,作,且,向左上偏移如图所示,
④当为下底边的时候,作,且,向右上偏移如图所示,
20、【答案】(1)证明见解析
(2)的值为1或
【解析】(1)证明:∵,
∴无论取何值,方程都有两个不相等的实数根.
(2)解:∵的两个实数根为,
∴.
∵,
∴,.
∴.
即.
解得或.
∴的值为1或.
21、【答案】(1)证明见解析
(2)
【解析】(1)证明:由翻折和正方形的性质可得,.
∴.
∴,即,
∵四边形是正方形,
∴.
∴.
∴.
(2)解:如图,延长交于点.
∵,
∴.
又∵,正方形边长为3,
∴
∴,
∴,,
设,则,
∴.
∵,即,
∴.
∴.
在中,,
∴.
解得:(舍),.
∴.
22、【答案】(1)
(2)该商品在第26天的日销售利润最大,最大日销售利润是1296元
【解析】解:(1)根据题意得:
当时,则;
当时,则;
∴;
(2)当时,;
∵抛物线开口向下,对称轴为直线,
∴当时,(元).
当时,,随增大而减小,
∴当时,(元).
∵,
∴该商品在第26天的日销售利润最大,最大日销售利润是1296元.
23、【答案】(1)证明见解析
(2)
【解析】(1)证明,∵,
∴.
又,
∴.
∴.
∴四边形是平行四边形.
∴.
作于.
又∵,
∴为的垂直平分线.
∴点在上.
∴.
即.又点在上,
∴为的切线;
(2)解:过点作于,连接.
∵为的垂直平分线,
∴.
∴.∴.
∴.
∴.
∵,
∴
∴,
又,
∴.
∴,.
∴.
∴.
∵,
∴.
∴.
∴.
∴.
24、【答案】(1)
(2)
(3),理由见解析
【解析】解:(1)∵抛物线与轴交于点,
∴,
解得:,
∴抛物线解析式为;
(2)∵点,点,
设直线的解析式为:.
∴,
∴,
直线的解析式为:.
同上,由点,可得直线的解析式为:.
令,得.
∴点的坐标为.
方法1:由题意可得:.
∴.
如图1,过点E作轴于点F.
∴.
∴.
∴.
又,
∴.
∴.
∵,
∴.
∵,
即.
方法2:如图2,延长与轴交于点,过点作于点,过点作轴于点.
∵,
∴.
∴.
∴.
∴.
∴.
∵,
,
∴.
∴
∴,即.
方法3:如图2,过点作于点.
∵.
∴.
∵,
∴.
∴.
(3)设点的坐标为,点的坐标为.
∵直线与不重合,
∴且且.
如图3,由点,点,
可得到直线的解析式为:.
∵,
∴可设直线的解析式为:.
将代入,
得.
∴.
∴点的坐标可以表示为.
设直线的解析式为:,
由点,点,得
,
解得.
∴直线的解析式为:.
同上,由点,点,
可得到直线的解析式为:.
∴.
∴.
∴.
∴点的横坐标为定值3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖北省潜江 天门 仙桃 江汉 油田数学中考真题名师详解版
(本卷共6页,满分120分,考试时间120分钟)
注意事项:
1.答题前,考生务必将自己的姓名,准考证号填写在试卷第1页装订线内和答题卡上,并在答题卡的规定位置贴好条形码,核准姓名和准考证号.
2.选择题的答案选出后,必须使用2B铅笔把答题卡上对应的答案标号涂黑.如需改动,先用橡皮擦干净后,再选涂其他答案标号.非选择题答案必须使用0,5mm黑色墨水签字笔填写在答题卡对应的区域内,写在本试卷上无效.
3.考试结束后,请将本试卷和答题卡一并交回.
一、选择题(本大题共10个小题,每小题3分,满分30分.在下列每个小题给出的四个答案中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分)
1. 的绝对值是( )
A. B. C. D.
2. 2023年全国高考报名人数约12910000人,数12910000用科学记数法表示( )
A. B. C. D.
3. 如图是一个立体图形的三视图,该立体图形是( )
A. 三棱柱 B. 圆柱 C. 三棱锥 D. 圆锥
4. 不等式组的解集是( )
A B. C. D.
5. 某班9名学生参加定点投篮测试,每人投篮10次,投中的次数统计如下:3,6,4,6,4,3,6,5,7.这组数据的中位数和众数分别是( )
A 5,4 B. 5,6 C. 6,5 D. 6,6
6. 在反比例函数的图象上有两点,当时,有,则的取值范围是( )
A. B. C. D.
7. 如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点外接圆的一部分,小正方形边长为1,图中阴影部分的面积为( )
A. B. C. D.
8. 如图,在中,,点在边上,且平分的周长,则的长是( )
A. B. C. D.
9. 拋物线与轴相交于点.下列结论:
①;②;③;④若点在抛物线上,且,则.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
10. 如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为(细实线)表示铁桶中水面高度,(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则随时间变化的函数图象大致为( )
A. B. C. D.
二、填空题(本大题共5个小题,每小题3分,满分15分,请将答案直接填在答线卡对应的横线上)
11. 计算的结果是_________.
12. 在平面直角坐标系中,若反比例函数的图象经过点和点,则的面积为_________.
13. 如图,在中,内切圆与分别相切于点,,连接的延长线交于点,则_________.
14. 有四张背面完全相同的卡片,正面分别画了等腰三角形,平行四边形,正五边形,圆,现将卡片背面朝上并洗匀,从中随机抽取一张,记下卡片上的图形后(不放回),再从中随机抽取一张,则抽取的两张卡片上的图形都是中心对称图形的概率为_________.
15. 如图,和都是等腰直角三角形,,点在内,,连接交于点交于点,连接.给出下面四个结论:①;②;③;④.其中所有正确结论的序号是_________.
三、解答题(本大题共9个题,满分75分)
16. (1)计算:;
(2)解分式方程:.
17. 为了解学生“防诈骗意识”情况,某校随机抽取了部分学生进行问卷调查,根据调查结果将“防诈骗意识”按A(很强),B(强),C(一般),D(弱),E(很弱)分为五个等级.将收集的数据整理后,绘制成如下不完整的统计图表.
等级 人数
A(很强) a
B(强) b
C(一般) 20
D(弱) 19
E(很弱) 16
(1)本次调查的学生共_________人;
(2)已知,请将条形统计图补充完整;
(3)若将A,B,C三个等级定为“防诈骗意识”合格,请估计该校2000名学生中"防诈骗意识”合格的学生有多少人?
18. 为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米,,求斜坡的长.(结果精确到米)(参考数据:)
19. 已知正六边形,请仅用无刻度的直尺完成下列作图(保留作图痕迹,不写作法,用虚线表示作图过程,实线表示作图结果).
(1)在图1中作出以为对角线的一个菱形;
(2)在图2中作出以为边的一个菱形.
20. 已知关于x的一元二次方程.
(1)求证:无论m取何值时,方程都有两个不相等的实数根;
(2)设该方程的两个实数根为a,b,若,求m的值.
21. 如图,将边长为3的正方形沿直线折叠,使点的对应点落在边上(点不与点重合),点落在点处,与交于点,折痕分别与边,交于点,连接.
(1)求证:;
(2)若,求的长.
22. 某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:
时间:第x(天)
日销售价(元/件) 50
日销售量(件)
(,x为整数)
设该商品的日销售利润为w元.
(1)直接写出w与x的函数关系式__________________;
(2)该商品在第几天的日销售利润最大?最大日销售利润是多少?
23. 如图,等腰内接于,,是边上的中线,过点作的平行线交的延长线于点,交于点,连接.
(1)求证:为切线;
(2)若的半径为,,求的长.
24. 如图1,在平面直角坐标系中,已知抛物线与轴交于点,与轴交于点,顶点为,连接.
(1)抛物线的解析式为__________________;(直接写出结果)
(2)在图1中,连接并延长交的延长线于点,求的度数;
(3)如图2,若动直线与抛物线交于两点(直线与不重合),连接,直线与交于点.当时,点的横坐标是否为定值,请说明理由.
参考答案及解析
一、选择题
1、【答案】D
【解析】解:.
因此选:D.
2、【答案】B
【解析】解:数12910000用科学记数法表示为.
因此选:B.
3、【答案】D
【解析】解:由主视图和左视图为三角形判断出是锥体,
根据俯视图是圆可判断出这个几何体应该是圆锥.
因此选:D.
4、【答案】A
【解析】解:
解不等式①得:,
解不等式②得:,
所以不等式组的解集为,
因此选A.
5、【答案】B
【解析】解:这组数据3,6,4,6,4,3,6,5,7中出现次数最多的是6,
众数是6.
将这组数据3,6,4,6,4,3,6,5,7按从小到大顺序排列是3,3,4,4,5,6, 6, 6, 7,
中位数为:5.
因此选:B
6、【答案】C
【解析】解:因为当时,有,
所以反比例函数的图象在一三象限,
所以
解得:,
因此选:C.
7、【答案】D
【解析】解:如图所示,作的垂直平分线,作的垂直平分线,设与相交于点O,连接,则点O是外接圆的圆心,
由题意得:,,,
∴,
∴是直角三角形,
∴,
∵,
∴
,
因此选:D.
8、【答案】C
【解析】解:如图所示,过点B作于点E,
∵在中,,
∴,
∵,
∴,
∴,
∵平分的周长,
∴,即,
又∵,
∴,
∴,
∴,
因此选C.
9、【答案】B
【解析】解:①由题意得:,
∴,
∵,
∴,
∴,所以①错误;
②∵抛物线与x轴相交于点.
∴有两个不相等的实数根,
∴,所以②正确;
③∵,
∴,所以③正确;
④∵抛物线与x轴相交于点.
∴抛物线的对称轴为:,
当点在抛物线上,且,
∴或,
解得:,所以④错误,
综上,②③正确,共2个,
因此选:B.
10、【答案】C
【解析】解:由图象知,时,铁桶注满了水,,是一条斜线段,,是一条水平线段,
当时,长方体水池开始注入水;当时,长方体水池中的水没过铁桶,水池中水面高度比之开始变得平缓;当时,长方体水池满了水,
所以开始是一段陡线段,后变缓,最后是一条水平线段,
观察函数图象,选项C符合题意,
因此选:C.
填空题
11、【答案】1
【解析】解:
,
因此答案为:1.
12、【答案】
【解析】解:反比例函数的图象经过点,
,
.
反比例函数为:.
反比例函数的图象经过点,
,
.
如图所示,过点作于点,过点作的延长线于点,设与轴的交点为,
,,
,,,
.
因此答案为:.
13、【答案】##度
【解析】解:如图所示,连接,设交于点H,
∵是的内切圆,
∴分别是的角平分线,
∴,
∵,
∴,
∴,
∴,
∵与分别相切于点,,
∴,
又∵,
∴是的垂直平分线,
∴,即,
∴,
因此答案为:.
14、【答案】
【解析】解:分别用,,,表示等腰三角形,平行四边形,正五边形,圆,画树状图如下:
依题意且由图知,共有12种等可能的结果,其中两次抽出的图形都是中心对称图形的有2种,
所以两次抽出的图形都是中心对称图形的概率为:.
因此答案为.
15、【答案】①③④
【解析】解:∵和都是等腰直角三角形,
∴,,,,
∵,,
∴,所以①正确;
∴,
∴,,所以③正确;
∵,,,
∴,;故②错误;
∴,
∵,
∴四边形是平行四边形,
∴,所以④正确;
因此答案为①③④.
解答题
16、【答案】(1);(2)
【解析】(1)解:原式
;
(2)解:两边乘以,得.
解得:.
经检验,是原分式方程的解.
17、【答案】(1)共100人
(2)见解析 (3)估计该校2000名学生中“防诈骗意识”合格的学生有1300人
【解析】解:(1)由统计图可知:(人);
故答案为100;
(2)由(1)得:,
∵,
∴,
补全条形统计图如下:
(3)由题意得:
(人).
所以估计该校2000名学生中“防诈骗意识”合格的学生有1300人.
18、【答案】斜坡的长约为10米
【解析】解:过点作于点,则四边形是矩形,
在中,,
.
∴.
∵,
∴在中,(米).
答:斜坡的长约为10米.
19、【答案】(1)见解析 (2)见解析
【解析】解:(1)如图所示,菱形即为所求(点,可以对调位置):
(2)如图,菱形即为所求.
是菱形,且要求为边,
①当为上底边的时候,作,且,向右下偏移,如图所示,
②当为上底边的时候,作,且,向左下偏移如图所示,
③当为下底边的时候,作,且,向左上偏移如图所示,
④当为下底边的时候,作,且,向右上偏移如图所示,
20、【答案】(1)证明见解析
(2)的值为1或
【解析】(1)证明:∵,
∴无论取何值,方程都有两个不相等的实数根.
(2)解:∵的两个实数根为,
∴.
∵,
∴,.
∴.
即.
解得或.
∴的值为1或.
21、【答案】(1)证明见解析
(2)
【解析】(1)证明:由翻折和正方形的性质可得,.
∴.
∴,即,
∵四边形是正方形,
∴.
∴.
∴.
(2)解:如图,延长交于点.
∵,
∴.
又∵,正方形边长为3,
∴
∴,
∴,,
设,则,
∴.
∵,即,
∴.
∴.
在中,,
∴.
解得:(舍),.
∴.
22、【答案】(1)
(2)该商品在第26天的日销售利润最大,最大日销售利润是1296元
【解析】解:(1)根据题意得:
当时,则;
当时,则;
∴;
(2)当时,;
∵抛物线开口向下,对称轴为直线,
∴当时,(元).
当时,,随增大而减小,
∴当时,(元).
∵,
∴该商品在第26天的日销售利润最大,最大日销售利润是1296元.
23、【答案】(1)证明见解析
(2)
【解析】(1)证明,∵,
∴.
又,
∴.
∴.
∴四边形是平行四边形.
∴.
作于.
又∵,
∴为的垂直平分线.
∴点在上.
∴.
即.又点在上,
∴为的切线;
(2)解:过点作于,连接.
∵为的垂直平分线,
∴.
∴.∴.
∴.
∴.
∵,
∴
∴,
又,
∴.
∴,.
∴.
∴.
∵,
∴.
∴.
∴.
∴.
24、【答案】(1)
(2)
(3),理由见解析
【解析】解:(1)∵抛物线与轴交于点,
∴,
解得:,
∴抛物线解析式为;
(2)∵点,点,
设直线的解析式为:.
∴,
∴,
直线的解析式为:.
同上,由点,可得直线的解析式为:.
令,得.
∴点的坐标为.
方法1:由题意可得:.
∴.
如图1,过点E作轴于点F.
∴.
∴.
∴.
又,
∴.
∴.
∵,
∴.
∵,
即.
方法2:如图2,延长与轴交于点,过点作于点,过点作轴于点.
∵,
∴.
∴.
∴.
∴.
∴.
∵,
,
∴.
∴
∴,即.
方法3:如图2,过点作于点.
∵.
∴.
∵,
∴.
∴.
(3)设点的坐标为,点的坐标为.
∵直线与不重合,
∴且且.
如图3,由点,点,
可得到直线的解析式为:.
∵,
∴可设直线的解析式为:.
将代入,
得.
∴.
∴点的坐标可以表示为.
设直线的解析式为:,
由点,点,得
,
解得.
∴直线的解析式为:.
同上,由点,点,
可得到直线的解析式为:.
∴.
∴.
∴.
∴点的横坐标为定值3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
