2023年湖北省随州市数学中考真题名师详解版 试卷
文档属性
| 名称 | 2023年湖北省随州市数学中考真题名师详解版 试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 11:42:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年湖北省随州市数学中考真题名师详解版
(考试时间120分钟 满分120分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如雷改动,用橡皮擦干净后,再选涂其他答案标号,答在试卷上无效.
3.非选择题作答:用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内,答在试卷上无效.
4.考生必须保持答题卡的整洁,考试结束后,请将本试卷和答题卡一并上交.
一、选择题(本大题共10小题,每小题3分,共30分.每小题给出的四个选项中,只有一个是正确的)
1. 实数﹣2023的绝对值是( )
A. 2023 B. ﹣2023 C. D.
2. 如图,直线,直线l与、相交,若图中,则为( )
A. B. C. D.
3. 如图是一个放在水平桌面上的圆柱体,该几何体的三视图中完全相同的是( )
A. 主视图和俯视图 B. 左视图和俯视图 C. 主视图和左视图 D. 三个视图均相同
4. 某班在开展劳动教育课程调查中发现,第一小组6名同学每周做家务的天数依次为3,7,5,6,5,4(单位:天),则这组数据的众数和中位数分别为( )
A. 5和5 B. 5和4 C. 5和6 D. 6和5
5. 甲、乙两个工程队共同修一条道路,其中甲工程队需要修9千米,乙工程队需要修12千米.已知乙工程队每个月比甲工程队多修1千米,最终用的时间比甲工程队少半个月.若设甲工程队每个月修x千米,则可列出方程为( )
A. B. C. D.
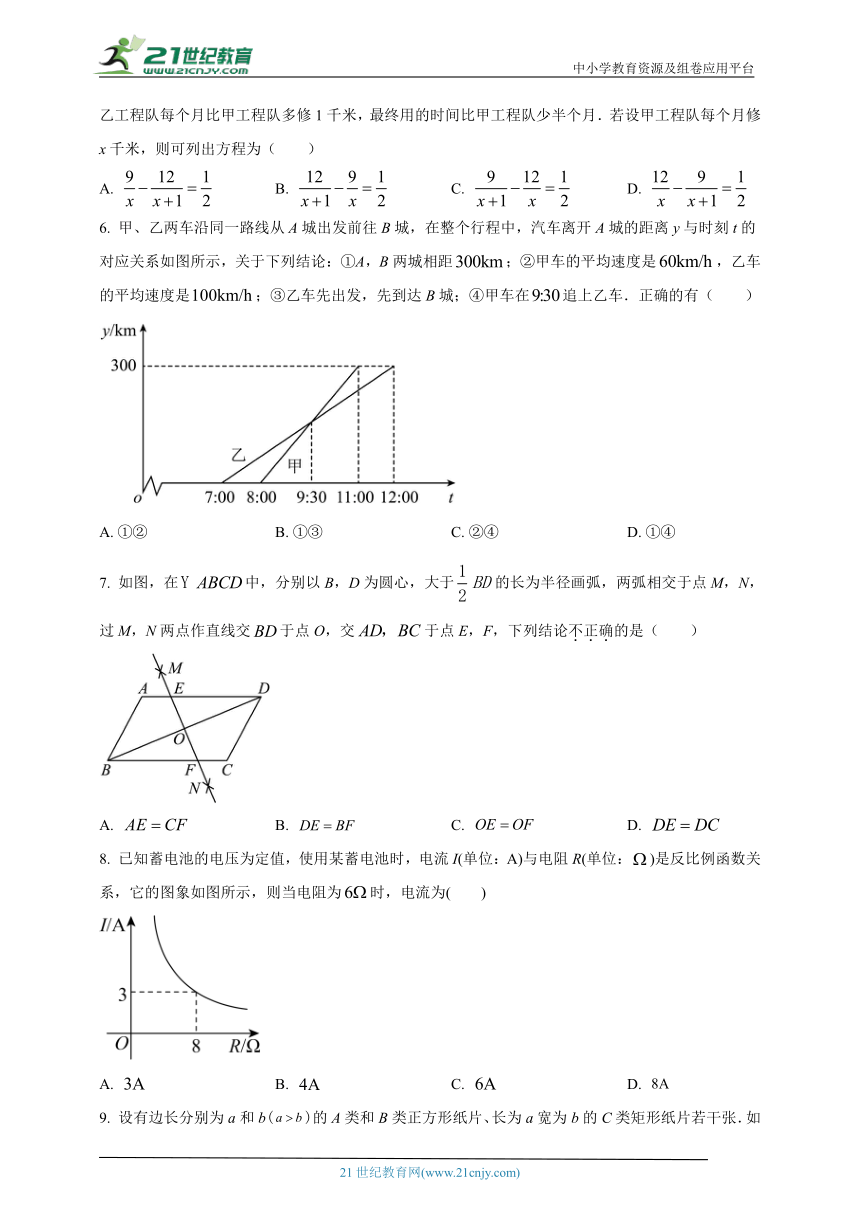
6. 甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距;②甲车的平均速度是,乙车的平均速度是;③乙车先出发,先到达B城;④甲车在追上乙车.正确的有( )
A. ①② B. ①③ C. ②④ D. ①④
7. 如图,在中,分别以B,D为圆心,大于的长为半径画弧,两弧相交于点M,N,过M,N两点作直线交于点O,交于点E,F,下列结论不正确的是( )
A. B. C. D.
8. 已知蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
A. B. C. D.
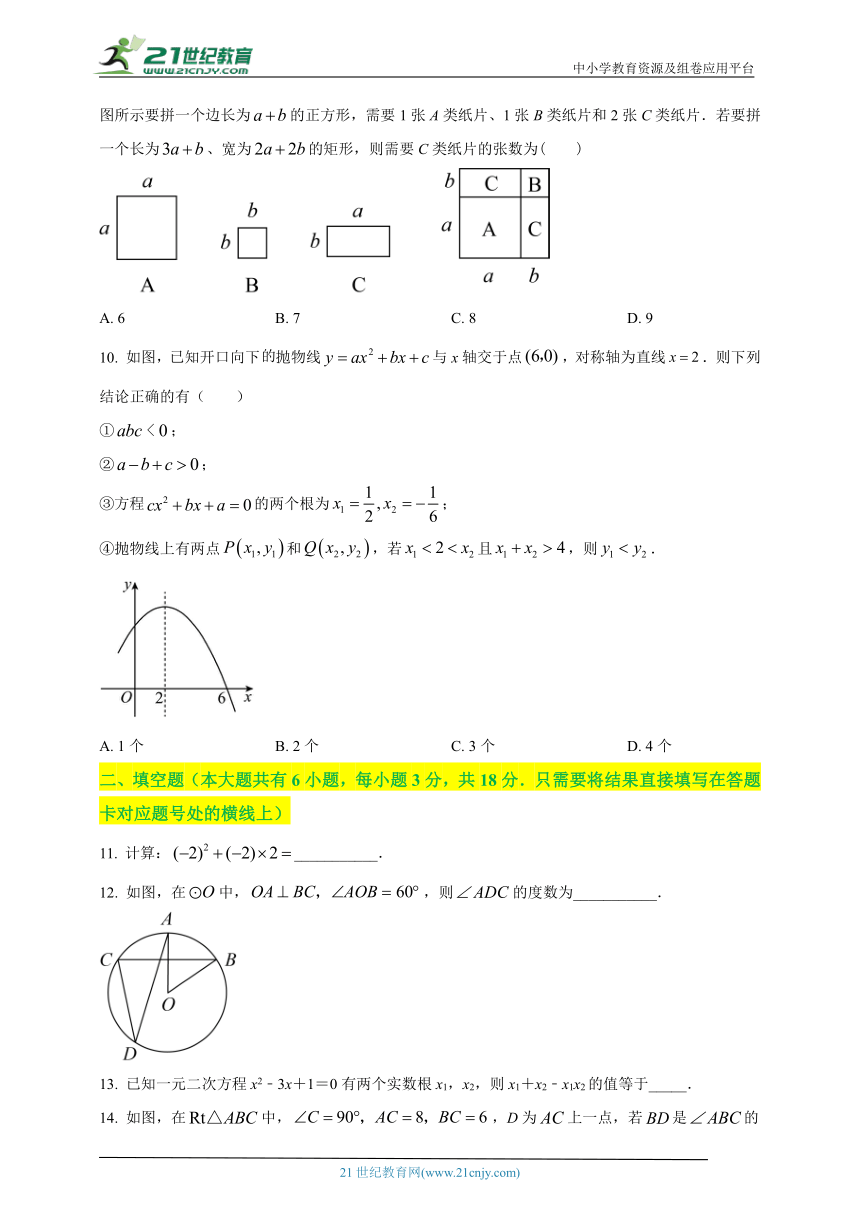
9. 设有边长分别为a和b()的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张.如图所示要拼一个边长为的正方形,需要1张A类纸片、1张B类纸片和2张C类纸片.若要拼一个长为、宽为的矩形,则需要C类纸片的张数为( )
A. 6 B. 7 C. 8 D. 9
10. 如图,已知开口向下抛物线与x轴交于点,对称轴为直线.则下列结论正确的有( )
①;
②;
③方程的两个根为;
④抛物线上有两点和,若且,则.
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共有6小题,每小题3分,共18分.只需要将结果直接填写在答题卡对应题号处的横线上)
11. 计算:___________.
12. 如图,在中,,则的度数为___________.
13. 已知一元二次方程x2﹣3x+1=0有两个实数根x1,x2,则x1+x2﹣x1x2的值等于_____.
14. 如图,在中,,D为上一点,若是的角平分线,则___________.
15. 某天老师给同学们出了一道趣味数学题:
设有编号为1-100的100盏灯,分别对应着编号为1-100的100个开关,灯分为“亮”和“不亮”两种状态,每按一次开关改变一次相对应编号的灯的状态,所有灯的初始状态为“不亮”.现有100个人,第1个人把所有编号是1的整数倍的开关按一次,第2个人把所有编号是2的整数倍的开关按一次,第3个人把所有编号是3的整数倍的开关按一次,……,第100个人把所有编号是100的整数倍的开关按一次.问最终状态为“亮”
的灯共有多少盏?
几位同学对该问题展开了讨论:
甲:应分析每个开关被按的次数找出规律:
乙:1号开关只被第1个人按了1次,2号开关被第1个人和第2个人共按了2次,3号开关被第1个人和第3个人共按了2次,……
丙:只有按了奇数次的开关所对应的灯最终是“亮”的状态.
根据以上同学的思维过程,可以得出最终状态为“亮”的灯共有___________盏.
16. 如图,在矩形中,,M是边上一动点(不含端点),将沿直线对折,得到.当射线交线段于点P时,连接,则面积为___________;的最大值为___________.
三、解答题(本大题共8小题,共72分.解答应写出必要的演算步骤、文字说明或证明过程)
17. 先化简,再求值:,其中.
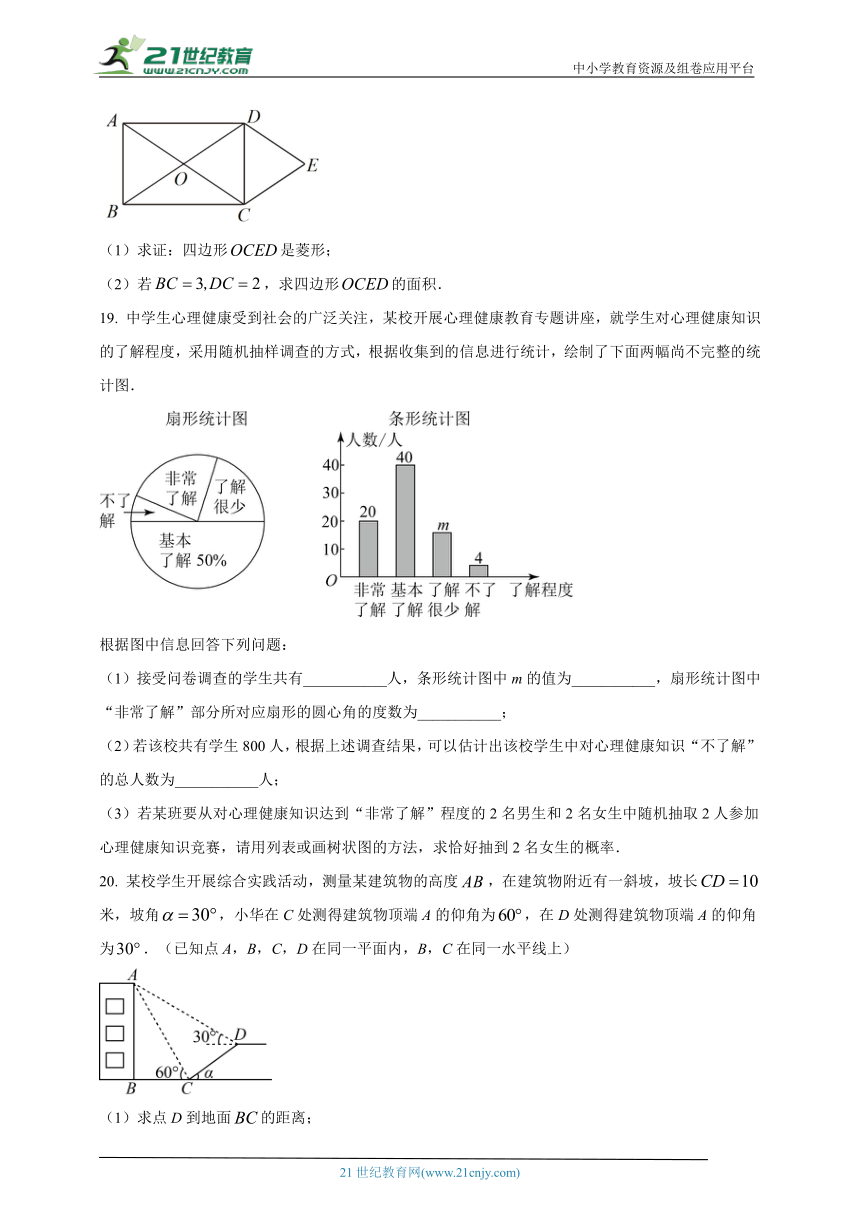
18. 如图,矩形的对角线,相交于点O,.
(1)求证:四边形是菱形;
(2)若,求四边形的面积.
19. 中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.
根据图中信息回答下列问题:
(1)接受问卷调查的学生共有___________人,条形统计图中m的值为___________,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为___________;
(2)若该校共有学生800人,根据上述调查结果,可以估计出该校学生中对心理健康知识“不了解”的总人数为___________人;
(3)若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛,请用列表或画树状图的方法,求恰好抽到2名女生的概率.
20. 某校学生开展综合实践活动,测量某建筑物的高度,在建筑物附近有一斜坡,坡长米,坡角,小华在C处测得建筑物顶端A的仰角为,在D处测得建筑物顶端A的仰角为.(已知点A,B,C,D在同一平面内,B,C在同一水平线上)
(1)求点D到地面的距离;
(2)求该建筑物的高度.
21. 如图,是的直径,点E,C在上,点C是的中点,垂直于过C点的直线,垂足为D,的延长线交直线于点F.
(1)求证:是的切线;
(2)若,,①求的半径;②求线段的长.
22. 为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元
(1)___________, ___________;
(2)求第x天的销售额W元与x之间的函数关系式;
(3)在试销售的30天中,销售额超过1000元的共有多少天?
23. 1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当的三个内角均小于时,
如图1,将绕,点C顺时针旋转得到,连接,
由,可知 ① 三角形,故,又,故,
由 ② 可知,当B,P,,A在同一条直线上时,取最小值,如图2,最小值为,此时的P点为该三角形的“费马点”,且有 ③ ;
已知当有一个内角大于或等于时,“费马点”为该三角形的某个顶点.如图3,若,则该三角形的“费马点”为 ④ 点.
(2)如图4,在中,三个内角均小于,且,已知点P为“费马点”,求的值;
(3)如图5,设村庄A,B,C连线构成一个三角形,且已知.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/,a元/,元/,选取合适的P的位置,可以使总的铺设成本最低为___________元.(结果用含a的式子表示)
24. 如图1,平面直角坐标系中,抛物线过点,和,连接,点为抛物线上一动点,过点作轴交直线于点,交轴于点.
(1)直接写出抛物线和直线的解析式;
(2)如图2,连接,当为等腰三角形时,求的值;
(3)当点在运动过程中,在轴上是否存在点,使得以,,为顶点的三角形与以,,为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】A
【解析】解:因为负数的绝对值等于它的相反数,
所以,﹣2023的绝对值等于2023.
因此选:A.
2、【答案】C
【解析】解:直线,
,
,
,
因此选C.
3、【答案】C
【解析】该几何体的三视图中完全相同的是主视图和左视图,均为矩形,俯视图是一个圆.
因此选:C.
4、【答案】A
【解析】解:将数据重新排列为3,4,5,5,6,7,
所以这组数据的众数为5,中位数,
因此选:A.
5、【答案】A
【解析】解:设甲工程队每个月修x千米,则乙工程队每个月修千米,
根据题意得,
因此选:A.
6、【答案】D
【解析】解:由图象知:
①A,B两城相距,所以此项正确;
②甲车的平均速度是,乙车的平均速度是,所以此项错误;
③乙车先出发,才到达B城,甲车后出发,就到达B城,所以此项错误;
④两车在时,行驶路程一样,即甲车在追上乙车,所以此项正确.
综上,①④说法正确,
因此选:D.
7、【答案】D
【解析】解:根据作图可知:垂直平分,
∴,
∴点O为的对称中心,
∴,
∵,
∴,
∴,
∵在中,,
∴,
∴,
∴,
∴,故B正确;
∴,
∴,故A正确;
∴四边形是菱形,
∴,故C正确;
与不一定相等,故D错误,
因此选:D.
8、【答案】B
【解析】解:设该反比函数解析式为,
由题意可知,当时,,
,
解得:,
设该反比函数解析式为,
当时,,
即电流为,
因此选:B.
9、【答案】C
【解析】解:长为,宽为的大长方形的面积为:
;
需要6张A卡片,2张B卡片和8张C卡片.
因此选:C.
10、【答案】B
【解析】解:由抛物线的开口可知:,由抛物线与y轴的交点可知:,由抛物线的对称轴可知:,∴,
∴,所以①正确;
∵抛物线与x轴交于点,对称轴为直线,
则另一个交点,
∴时,,
∴,所以②正确;
∵抛物线与x轴交于点和,
∴的两根为6和,
∴,,则,,
如果方程的两个根为成立,
则,
而,∴,
∴方程的两个根为不成立,所以③不正确;
∵,∴P、Q两点分布在对称轴的两侧,
∵,
即到对称轴的距离小于到对称轴的距离,
∴,所以④不正确.
综上,正确的有①②,
因此选:B.
二、填空题
11、【答案】0
【解析】解:.
因此答案为:0.
12、【答案】##30度
【解析】解:∵,
∴,
∴,
因此答案为:.
13、【答案】2
【解析】
解:根据根与系数的关系得:
x1+x2=3,x1x2=1,
∴x1+x2﹣x1x2=3﹣1=2.
因此答案为:2.
14、【答案】3
【解析】解:如图,过点D作的垂线,垂足为P,
在中,∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
∴,,
设,
在中,∵,,
∴,
∴,
∴.
因此答案为:3.
15、【答案】10
【解析】所有灯的初始状态为“不亮”,按奇数次,则状态为“亮”,按偶数次,则状态为“不亮”;
因数的个数为奇数的自然数只有完全平方数,1-100中,完全平方数为1,4,9,16,25,36,49,64,81,100;有10个数,故有10盏灯被按奇数次,为“亮”的状态;
因此答案为:10.
16、【答案】 ①. ②.
【解析】解:由题意可得的面积等于矩形的一半,
∴的面积为,
在中,,
∴当最大时,即最大,
由题意可得点N是在以D为圆心4为半径的圆上运动,当射线与圆相切时,最大,此时C、N、M三点共线,如图:
根据题意得:,,
∴,,
∴
∵,
∴,
∴,
∴,
∴,
在中,,
因此答案为:,.
三、解答题
17、【答案】,.
【解析】解:
,
当时,原式.
18、【答案】(1)见解析 (2)3
【解析】(1)证明:∵,
∴四边形是平行四边形,
又∵矩形中,,
∴平行四边形是菱形;
(2)解:矩形的面积为,
∴的面积为,
∴菱形的面积为.
19、【答案】(1)80,16,
(2)40 (3)恰好抽到2名女生的概率为.
【解析】解:(1)接受问卷调查的学生共有(人,
(人,
扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为;
故答案为:80,16,;
(2)根据题意得:
(人,
答:估计出该校学生中对心理健康知识“不了解”的总人数为40人;
故答案为:40;
(3)由题意列树状图:
由树状图可知,所有等可能的结果有12种,恰好抽到2名女生的结果有2种,
∴恰好抽到2名女生的概率为.
20、【答案】(1)5米 (2)米
【解析】解:(1)过点D作,
由题意可得,
∴在Rt中,,
即点D到地面的距离为5米;
(2)如图,
由题意可得,,
∴,
又∵,
∴,
∴
∴在Rt中,,即,
解得,
在Rt中,,即,
解得,
答:该建筑物的高度为15米.
21、【答案】(1)证明见解析
(2)①3;②2
【解析】(1)证明:如图,连接,
点C是的中点,
,
,
,
,
,
,
,
,
是的半径,
是的切线;
(2)解:①如图,连接,
是直径,
,
,
,
,
,
,
,
,
,
的半径为;
②由(1)可知,,
,
,,
,
,
,
,
,
,
,
.
22、【答案】(1),
(2)时,,当时,
(3)7天
【解析】解:(1)∵第5天售价为50元/千克,第10天售价为40元/千克,
∴,解得,
因此答案为:,;
(2)由题意当时,,
当时,,
(3)由题意当时,,
∵,
∴当时,最大为,
当时,,
由时,解得,
又∵x为整数,且,
∴当时,随的增大而增大,
∴第至天,销售额超过1000元,共7天.
23、【答案】(1)①等边;②两点之间线段最短;③;④A.
(2)
(3)
【解析】解:(1)∵,
∴为等边三角形;
∴,,
又,故,
由两点之间线段最短可知,当B,P,,A在同一条直线上时,取最小值,
最小值为,此时的P点为该三角形的“费马点”,
∴,,
∴,,
又∵,
∴,
∴,
∴;
∵,
∴,,
∴,,
∴三个顶点中,顶点A到另外两个顶点的距离和最小.
又∵已知当有一个内角大于或等于时,“费马点”为该三角形的某个顶点.
∴该三角形的“费马点”为点A,
因此答案为:①等边;②两点之间线段最短;③;④.
(2)将绕,点C顺时针旋转得到,连接,
由(1)可知当B,P,,A在同一条直线上时,取最小值,最小值为,
∵,
∴,
又∵
∴,
由旋转性质可知:,
∴,
∴最小值为,
(3)∵总铺设成本
∴当最小时,总的铺设成本最低,
将绕,点C顺时针旋转得到,连接,
由旋转性质可知:,,,,
∴,
∴,
当B,P,,A在同一条直线上时,取最小值,即取最小值为,
过点作,垂足为,
∵,,
∴,
∴,
∴,
∴,
∴
的最小值为
总的铺设成本(元)
因此答案为:
24、【答案】(1)抛物线:;直线:
(2)或或
(3),或,或,
【解析】解:(1)抛物线过点,,
抛物线的表达式为,
将点代入上式,得,
.
抛物线的表达式为,即.
设直线的表达式为,
将点,代入上式,
得,
解得.
直线的表达式为.
(2)点在直线上,且,
点的坐标为.
,,.
当为等腰三角形时,
①若,则,
即,
解得.
②若,则,
即,
解得或(舍去).
③若,则,
即,
解得(舍去)或.
综上,或或.
(3)点与点相对应,
或.
①若点在点左侧,
则,,.
当,即时,
直线的表达式为,
,解得或(舍去).
,即.
,即,
解得.
,.
当,即时,
,,
,即,
解得(舍去)或(舍去).
②若点点右侧,
则,.
当,即时,
直线的表达式为,
,解得或(舍去),
,
,即,
解得.
,.
当,即时,
,.
,即,
解得或(舍去).
,.
综上,,或,或,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年湖北省随州市数学中考真题名师详解版
(考试时间120分钟 满分120分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如雷改动,用橡皮擦干净后,再选涂其他答案标号,答在试卷上无效.
3.非选择题作答:用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内,答在试卷上无效.
4.考生必须保持答题卡的整洁,考试结束后,请将本试卷和答题卡一并上交.
一、选择题(本大题共10小题,每小题3分,共30分.每小题给出的四个选项中,只有一个是正确的)
1. 实数﹣2023的绝对值是( )
A. 2023 B. ﹣2023 C. D.
2. 如图,直线,直线l与、相交,若图中,则为( )
A. B. C. D.
3. 如图是一个放在水平桌面上的圆柱体,该几何体的三视图中完全相同的是( )
A. 主视图和俯视图 B. 左视图和俯视图 C. 主视图和左视图 D. 三个视图均相同
4. 某班在开展劳动教育课程调查中发现,第一小组6名同学每周做家务的天数依次为3,7,5,6,5,4(单位:天),则这组数据的众数和中位数分别为( )
A. 5和5 B. 5和4 C. 5和6 D. 6和5
5. 甲、乙两个工程队共同修一条道路,其中甲工程队需要修9千米,乙工程队需要修12千米.已知乙工程队每个月比甲工程队多修1千米,最终用的时间比甲工程队少半个月.若设甲工程队每个月修x千米,则可列出方程为( )
A. B. C. D.
6. 甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距;②甲车的平均速度是,乙车的平均速度是;③乙车先出发,先到达B城;④甲车在追上乙车.正确的有( )
A. ①② B. ①③ C. ②④ D. ①④
7. 如图,在中,分别以B,D为圆心,大于的长为半径画弧,两弧相交于点M,N,过M,N两点作直线交于点O,交于点E,F,下列结论不正确的是( )
A. B. C. D.
8. 已知蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
A. B. C. D.
9. 设有边长分别为a和b()的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张.如图所示要拼一个边长为的正方形,需要1张A类纸片、1张B类纸片和2张C类纸片.若要拼一个长为、宽为的矩形,则需要C类纸片的张数为( )
A. 6 B. 7 C. 8 D. 9
10. 如图,已知开口向下抛物线与x轴交于点,对称轴为直线.则下列结论正确的有( )
①;
②;
③方程的两个根为;
④抛物线上有两点和,若且,则.
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共有6小题,每小题3分,共18分.只需要将结果直接填写在答题卡对应题号处的横线上)
11. 计算:___________.
12. 如图,在中,,则的度数为___________.
13. 已知一元二次方程x2﹣3x+1=0有两个实数根x1,x2,则x1+x2﹣x1x2的值等于_____.
14. 如图,在中,,D为上一点,若是的角平分线,则___________.
15. 某天老师给同学们出了一道趣味数学题:
设有编号为1-100的100盏灯,分别对应着编号为1-100的100个开关,灯分为“亮”和“不亮”两种状态,每按一次开关改变一次相对应编号的灯的状态,所有灯的初始状态为“不亮”.现有100个人,第1个人把所有编号是1的整数倍的开关按一次,第2个人把所有编号是2的整数倍的开关按一次,第3个人把所有编号是3的整数倍的开关按一次,……,第100个人把所有编号是100的整数倍的开关按一次.问最终状态为“亮”
的灯共有多少盏?
几位同学对该问题展开了讨论:
甲:应分析每个开关被按的次数找出规律:
乙:1号开关只被第1个人按了1次,2号开关被第1个人和第2个人共按了2次,3号开关被第1个人和第3个人共按了2次,……
丙:只有按了奇数次的开关所对应的灯最终是“亮”的状态.
根据以上同学的思维过程,可以得出最终状态为“亮”的灯共有___________盏.
16. 如图,在矩形中,,M是边上一动点(不含端点),将沿直线对折,得到.当射线交线段于点P时,连接,则面积为___________;的最大值为___________.
三、解答题(本大题共8小题,共72分.解答应写出必要的演算步骤、文字说明或证明过程)
17. 先化简,再求值:,其中.
18. 如图,矩形的对角线,相交于点O,.
(1)求证:四边形是菱形;
(2)若,求四边形的面积.
19. 中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.
根据图中信息回答下列问题:
(1)接受问卷调查的学生共有___________人,条形统计图中m的值为___________,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为___________;
(2)若该校共有学生800人,根据上述调查结果,可以估计出该校学生中对心理健康知识“不了解”的总人数为___________人;
(3)若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛,请用列表或画树状图的方法,求恰好抽到2名女生的概率.
20. 某校学生开展综合实践活动,测量某建筑物的高度,在建筑物附近有一斜坡,坡长米,坡角,小华在C处测得建筑物顶端A的仰角为,在D处测得建筑物顶端A的仰角为.(已知点A,B,C,D在同一平面内,B,C在同一水平线上)
(1)求点D到地面的距离;
(2)求该建筑物的高度.
21. 如图,是的直径,点E,C在上,点C是的中点,垂直于过C点的直线,垂足为D,的延长线交直线于点F.
(1)求证:是的切线;
(2)若,,①求的半径;②求线段的长.
22. 为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元
(1)___________, ___________;
(2)求第x天的销售额W元与x之间的函数关系式;
(3)在试销售的30天中,销售额超过1000元的共有多少天?
23. 1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当的三个内角均小于时,
如图1,将绕,点C顺时针旋转得到,连接,
由,可知 ① 三角形,故,又,故,
由 ② 可知,当B,P,,A在同一条直线上时,取最小值,如图2,最小值为,此时的P点为该三角形的“费马点”,且有 ③ ;
已知当有一个内角大于或等于时,“费马点”为该三角形的某个顶点.如图3,若,则该三角形的“费马点”为 ④ 点.
(2)如图4,在中,三个内角均小于,且,已知点P为“费马点”,求的值;
(3)如图5,设村庄A,B,C连线构成一个三角形,且已知.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/,a元/,元/,选取合适的P的位置,可以使总的铺设成本最低为___________元.(结果用含a的式子表示)
24. 如图1,平面直角坐标系中,抛物线过点,和,连接,点为抛物线上一动点,过点作轴交直线于点,交轴于点.
(1)直接写出抛物线和直线的解析式;
(2)如图2,连接,当为等腰三角形时,求的值;
(3)当点在运动过程中,在轴上是否存在点,使得以,,为顶点的三角形与以,,为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.
参考答案及解析
一、选择题
1、【答案】A
【解析】解:因为负数的绝对值等于它的相反数,
所以,﹣2023的绝对值等于2023.
因此选:A.
2、【答案】C
【解析】解:直线,
,
,
,
因此选C.
3、【答案】C
【解析】该几何体的三视图中完全相同的是主视图和左视图,均为矩形,俯视图是一个圆.
因此选:C.
4、【答案】A
【解析】解:将数据重新排列为3,4,5,5,6,7,
所以这组数据的众数为5,中位数,
因此选:A.
5、【答案】A
【解析】解:设甲工程队每个月修x千米,则乙工程队每个月修千米,
根据题意得,
因此选:A.
6、【答案】D
【解析】解:由图象知:
①A,B两城相距,所以此项正确;
②甲车的平均速度是,乙车的平均速度是,所以此项错误;
③乙车先出发,才到达B城,甲车后出发,就到达B城,所以此项错误;
④两车在时,行驶路程一样,即甲车在追上乙车,所以此项正确.
综上,①④说法正确,
因此选:D.
7、【答案】D
【解析】解:根据作图可知:垂直平分,
∴,
∴点O为的对称中心,
∴,
∵,
∴,
∴,
∵在中,,
∴,
∴,
∴,
∴,故B正确;
∴,
∴,故A正确;
∴四边形是菱形,
∴,故C正确;
与不一定相等,故D错误,
因此选:D.
8、【答案】B
【解析】解:设该反比函数解析式为,
由题意可知,当时,,
,
解得:,
设该反比函数解析式为,
当时,,
即电流为,
因此选:B.
9、【答案】C
【解析】解:长为,宽为的大长方形的面积为:
;
需要6张A卡片,2张B卡片和8张C卡片.
因此选:C.
10、【答案】B
【解析】解:由抛物线的开口可知:,由抛物线与y轴的交点可知:,由抛物线的对称轴可知:,∴,
∴,所以①正确;
∵抛物线与x轴交于点,对称轴为直线,
则另一个交点,
∴时,,
∴,所以②正确;
∵抛物线与x轴交于点和,
∴的两根为6和,
∴,,则,,
如果方程的两个根为成立,
则,
而,∴,
∴方程的两个根为不成立,所以③不正确;
∵,∴P、Q两点分布在对称轴的两侧,
∵,
即到对称轴的距离小于到对称轴的距离,
∴,所以④不正确.
综上,正确的有①②,
因此选:B.
二、填空题
11、【答案】0
【解析】解:.
因此答案为:0.
12、【答案】##30度
【解析】解:∵,
∴,
∴,
因此答案为:.
13、【答案】2
【解析】
解:根据根与系数的关系得:
x1+x2=3,x1x2=1,
∴x1+x2﹣x1x2=3﹣1=2.
因此答案为:2.
14、【答案】3
【解析】解:如图,过点D作的垂线,垂足为P,
在中,∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
∴,,
设,
在中,∵,,
∴,
∴,
∴.
因此答案为:3.
15、【答案】10
【解析】所有灯的初始状态为“不亮”,按奇数次,则状态为“亮”,按偶数次,则状态为“不亮”;
因数的个数为奇数的自然数只有完全平方数,1-100中,完全平方数为1,4,9,16,25,36,49,64,81,100;有10个数,故有10盏灯被按奇数次,为“亮”的状态;
因此答案为:10.
16、【答案】 ①. ②.
【解析】解:由题意可得的面积等于矩形的一半,
∴的面积为,
在中,,
∴当最大时,即最大,
由题意可得点N是在以D为圆心4为半径的圆上运动,当射线与圆相切时,最大,此时C、N、M三点共线,如图:
根据题意得:,,
∴,,
∴
∵,
∴,
∴,
∴,
∴,
在中,,
因此答案为:,.
三、解答题
17、【答案】,.
【解析】解:
,
当时,原式.
18、【答案】(1)见解析 (2)3
【解析】(1)证明:∵,
∴四边形是平行四边形,
又∵矩形中,,
∴平行四边形是菱形;
(2)解:矩形的面积为,
∴的面积为,
∴菱形的面积为.
19、【答案】(1)80,16,
(2)40 (3)恰好抽到2名女生的概率为.
【解析】解:(1)接受问卷调查的学生共有(人,
(人,
扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为;
故答案为:80,16,;
(2)根据题意得:
(人,
答:估计出该校学生中对心理健康知识“不了解”的总人数为40人;
故答案为:40;
(3)由题意列树状图:
由树状图可知,所有等可能的结果有12种,恰好抽到2名女生的结果有2种,
∴恰好抽到2名女生的概率为.
20、【答案】(1)5米 (2)米
【解析】解:(1)过点D作,
由题意可得,
∴在Rt中,,
即点D到地面的距离为5米;
(2)如图,
由题意可得,,
∴,
又∵,
∴,
∴
∴在Rt中,,即,
解得,
在Rt中,,即,
解得,
答:该建筑物的高度为15米.
21、【答案】(1)证明见解析
(2)①3;②2
【解析】(1)证明:如图,连接,
点C是的中点,
,
,
,
,
,
,
,
,
是的半径,
是的切线;
(2)解:①如图,连接,
是直径,
,
,
,
,
,
,
,
,
,
的半径为;
②由(1)可知,,
,
,,
,
,
,
,
,
,
,
.
22、【答案】(1),
(2)时,,当时,
(3)7天
【解析】解:(1)∵第5天售价为50元/千克,第10天售价为40元/千克,
∴,解得,
因此答案为:,;
(2)由题意当时,,
当时,,
(3)由题意当时,,
∵,
∴当时,最大为,
当时,,
由时,解得,
又∵x为整数,且,
∴当时,随的增大而增大,
∴第至天,销售额超过1000元,共7天.
23、【答案】(1)①等边;②两点之间线段最短;③;④A.
(2)
(3)
【解析】解:(1)∵,
∴为等边三角形;
∴,,
又,故,
由两点之间线段最短可知,当B,P,,A在同一条直线上时,取最小值,
最小值为,此时的P点为该三角形的“费马点”,
∴,,
∴,,
又∵,
∴,
∴,
∴;
∵,
∴,,
∴,,
∴三个顶点中,顶点A到另外两个顶点的距离和最小.
又∵已知当有一个内角大于或等于时,“费马点”为该三角形的某个顶点.
∴该三角形的“费马点”为点A,
因此答案为:①等边;②两点之间线段最短;③;④.
(2)将绕,点C顺时针旋转得到,连接,
由(1)可知当B,P,,A在同一条直线上时,取最小值,最小值为,
∵,
∴,
又∵
∴,
由旋转性质可知:,
∴,
∴最小值为,
(3)∵总铺设成本
∴当最小时,总的铺设成本最低,
将绕,点C顺时针旋转得到,连接,
由旋转性质可知:,,,,
∴,
∴,
当B,P,,A在同一条直线上时,取最小值,即取最小值为,
过点作,垂足为,
∵,,
∴,
∴,
∴,
∴,
∴
的最小值为
总的铺设成本(元)
因此答案为:
24、【答案】(1)抛物线:;直线:
(2)或或
(3),或,或,
【解析】解:(1)抛物线过点,,
抛物线的表达式为,
将点代入上式,得,
.
抛物线的表达式为,即.
设直线的表达式为,
将点,代入上式,
得,
解得.
直线的表达式为.
(2)点在直线上,且,
点的坐标为.
,,.
当为等腰三角形时,
①若,则,
即,
解得.
②若,则,
即,
解得或(舍去).
③若,则,
即,
解得(舍去)或.
综上,或或.
(3)点与点相对应,
或.
①若点在点左侧,
则,,.
当,即时,
直线的表达式为,
,解得或(舍去).
,即.
,即,
解得.
,.
当,即时,
,,
,即,
解得(舍去)或(舍去).
②若点点右侧,
则,.
当,即时,
直线的表达式为,
,解得或(舍去),
,
,即,
解得.
,.
当,即时,
,.
,即,
解得或(舍去).
,.
综上,,或,或,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
